Деятельностный подход при обучении решению задач календаря (локальная система задач)

В работе представлена разработка локальной системы задач по теме "Задачи календаря" для учащихся 5 класса; презентация с задачами на урок и разбор задач. Приведено описание деятельностного подхода при решении задач, локальной системы задач. Работа будет полезна как учителям, так и студентам математиеского факультета.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Задачи календаря»

Три качества – обширные знания,

привычка мыслить и благородство чувств –

необходимы для того, чтобы человек

был образованным в полном смысле этого слова.

Г. Чернышевский

Деятельностный подход в процессе решения задач

Основной задачей обучения математике в общеобразовательной школе является обеспечение прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования.

Наряду с этой задачей перед учителем стоит проблема: научить школьников рассуждать, научить мыслить. Ни один школьный предмет не может конкурировать с возможностями математики в воспитании мыслящей личности.

Достижение необходимого развивающего эффекта обучения математике возможно на базе реализации деятельностного подхода, который направлен на развитие каждого ученика, на формирование индивидуальных способностей учащихся.

Деятельностный подход в обучении математике, а также требования к задачам, позволяют сделать вывод о том, что задачи, решаемые в курсе математики, должны возникать из проблемных ситуаций в различных предметных областях. Решая их математическими средствами, ученики получают возможность последовательно проходить по всем аспектам математической деятельности.

При изучении математики в школе имеют место такие виды деятельности учащихся, как: введение понятия; изучение утверждений (обнаружение, формулировка аксиомы или теоремы, доказательство теорем); процесс решения задач.

Процесс решения задачи (ПРЗ) мы рассматриваем как третий вид деятельности учащихся при обучении математике. В этом случае деятельность осуществляется для усвоения новых математических фактов (понятия или его свойства, алгоритма, метода). Причем данная потребность учащимися часто не осознается, но математические задачи как средство создания проблемной ситуации являются незаменимым способом мотивации школьников. Смыслообразующим мотивом процесса решения задачи, побуждающим фактором является нахождение решения задачи. Общая цель деятельности – нахождение ответа на главный вопрос задачи, задает следующие действия:

изучение структуры задачи;
поиск плана решения задачи;
осуществление плана решения (синтез);
проверка решения задачи;
изучение полученных результатов

Начиная с работы Д. Пойа, обозначившего структуру и содержание процесса решения задачи (рис. 1), исследование проблемы обучения решению задач продолжаются.

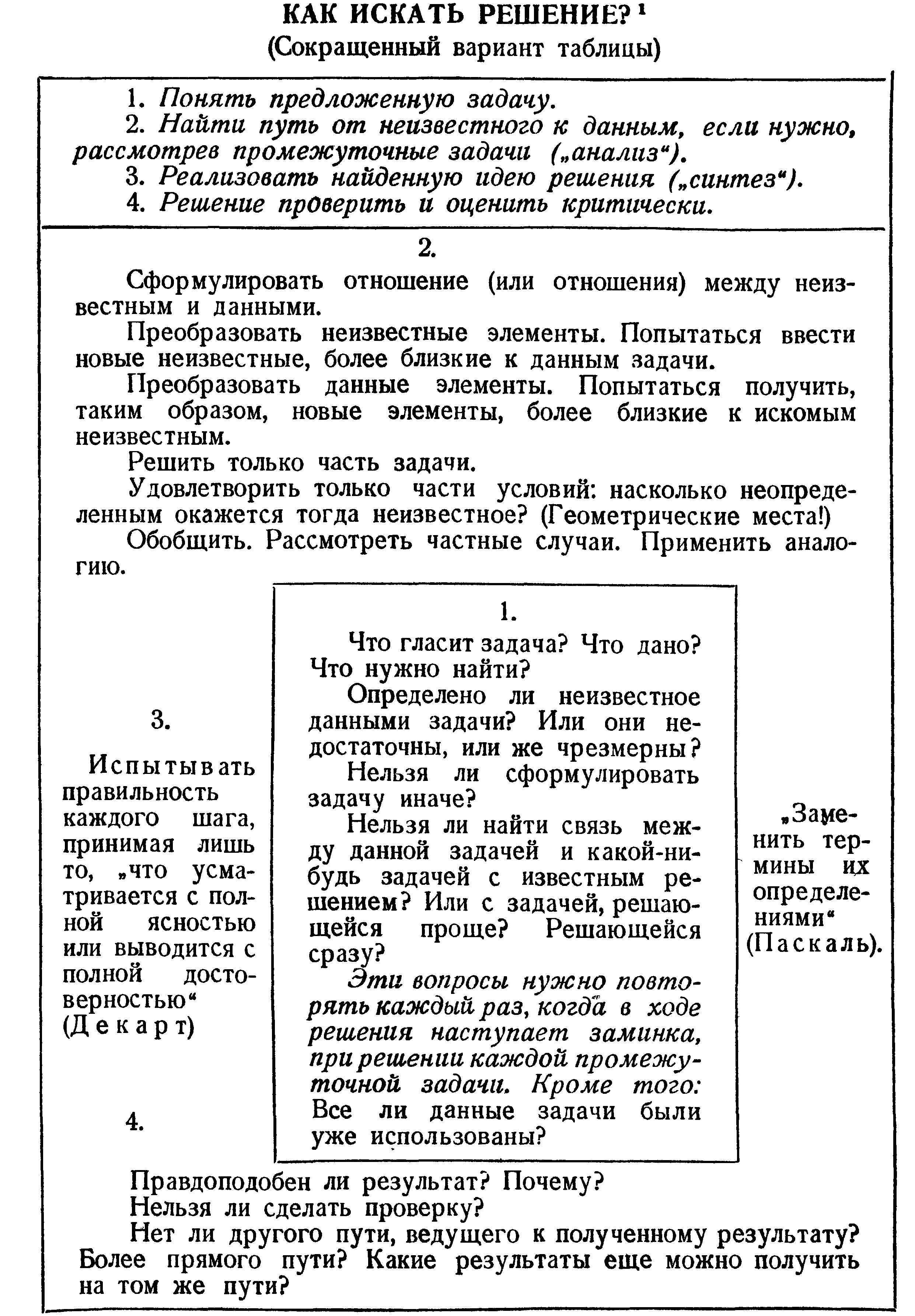
Рис. 1. Как искать решение

Локальная система задач как средство реализации деятельностного подхода

Совокупность задач, предназначенных для усвоения изучаемой темы, называют локальной системой задач. В методике преподавания математики сформулированы и обоснованы требования к системе как геометрических, так и других видов задач:

1) всестороннее отражение в системе задач признаков изучаемого понятия, свойств фигур во взаимосвязи с ранее изученными фактами посредством следующих задач:

взаимно-обратные;
задачи, имеющие различные способы решения;
задачи «без ограничений»;
«потенциально полезные».

2) сложность задач локальной системы различна;

3) наличие в системе задач, различающихся формой предъявления;

4) наличие задач с практической, занимательной (для младших школьников) фабулой, межпредметного содержания.

Как правило, задачи в локальной системе задач расположены по их сложности, в соответствии с дидактическим принципом доступности. Под сложностью задачи понимается сложность структурной формулы решения, построенной на основе аналитико-синтетического поиска. Требование наличия задач различной сложности позволяет не только осуществлять дифференцированный подход к обучению, но и развивать, например, умение проводить целенаправленный поиск плана решения задач методом восходящего или нисходящего анализа у учащихся, не владеющих ими.

Деятельность процесса решения задач очень подвижна, она превращается в действие, например, при решении задачи с дидактической функцией: задач на распознавание или задач, ориентированных на формирование алгоритма. В задачах более сложной структуры (задачах с познавательной функцией) у многих учащихся действия превращаются в операции, если способ решения достаточно сформировался у школьника.

В процессе решения «потенциально полезных» и взаимно-обратных задач учащимися устанавливаются существенные связи между знаниями различных разделов курса алгебры, способствующие углублению и расширению их знаний.

Процесс решения «потенциально полезных» задач и задач «без ограничений» способствует формированию умений учащихся вычленять, а затем формулировать новые задачи, ставить цели, намечать пути их достижения. Решение задач «без ограничений» развивает способность видеть частные, особые случаи, содействует формированию вариативности мышления. Важно отметить, что задачи «без ограничений» являются средством формирования метода полной индукции — одного из видов умозаключений, основанных «на рассмотрении в с е х единичных и частных суждений (случаев), относящихся к рассматриваемой ситуации.

Задачи, имеющие более одного способа решения, способствуют развитию эвристической деятельности учащихся. В поиске плана решения таких задач имеется возможность «открывать» способ решения, а не только ориентироваться на прием, используемый в аналогичных ситуациях. Вместе с тем все выделенные задачи показывают первостепенную роль качественно усвоенных знаний и, обратно, процесс решения задач способствует формированию изучаемых понятий.

Задачи календаря для учащихся 5 классов

«СКОЛЬКО МНЕ НЕДЕЛЬ?»

Чтобы научится по числу лет быстро определять число заключающихся в них недель, нужно только уметь ускоренно множить на 52, т.е. на число недель в году.

Пример. Найти количество недель, заключенных в 36 гг [4, с. 134].

Решение. По условию задачи, нужно перемножить 36 на 52. Перемножить довольно просто: 52 состоит из 50 и 2; 36 умножается на 5 через деление пополам; получается 18 – это первые две цифры результата. Далее умножение 36 на 2 делается как обыкновенно, получают 72, которые и приписываются к прежним 18-и:1872.

Ответ: 1872.

«СКОЛЬКО МНЕ ДНЕЙ?»

Если спрашивают не о числе недель, а о числе дней, то прибегают к такому приему: половину числа лет множат на 73 и приписывают нуль – результат и будет искомым числом.

Пример. Сколько Алеше дней, если ему 24 г [4, с. 135].

Решение. По условию задачи, нужно перемножить 12 на 73. Располагаем числа по следующей схеме, одно под другим:

1 2

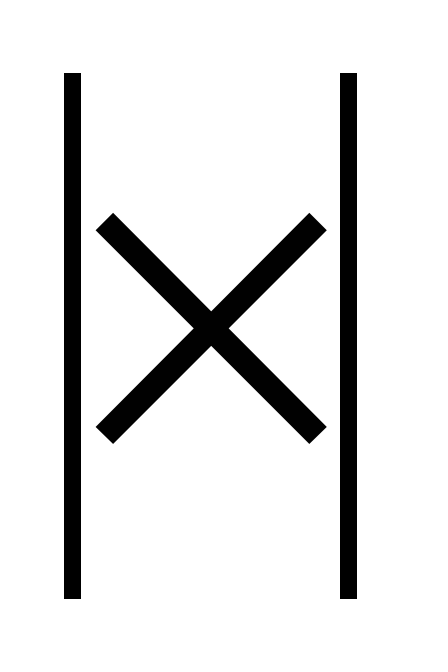
7 3

Теперь последовательно производим следующие действия:

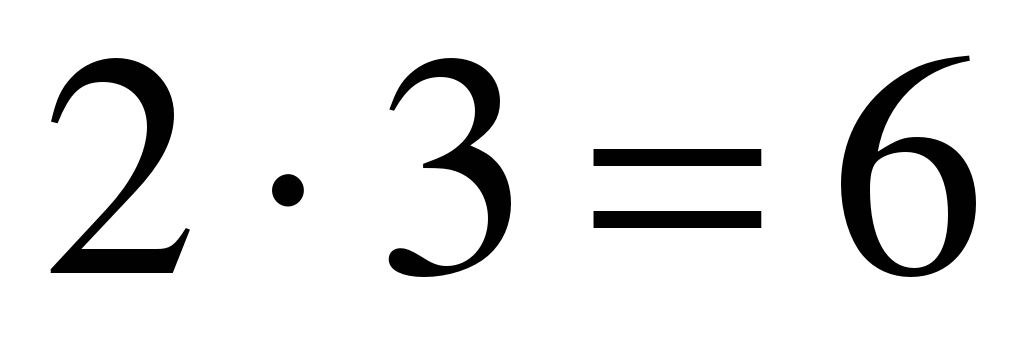– последняя цифра результата;
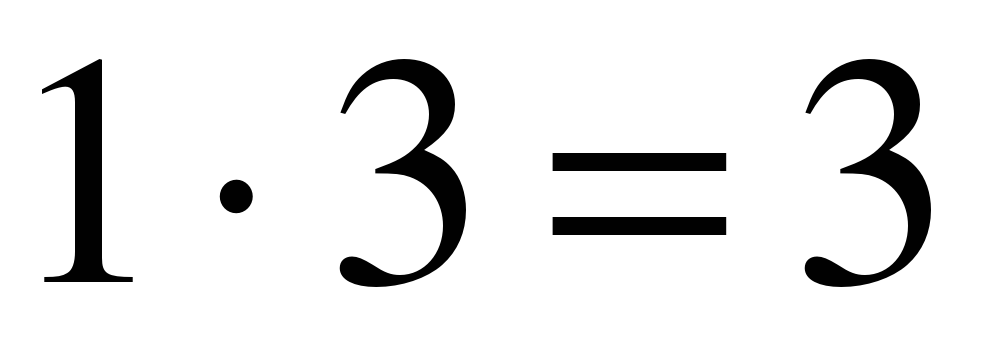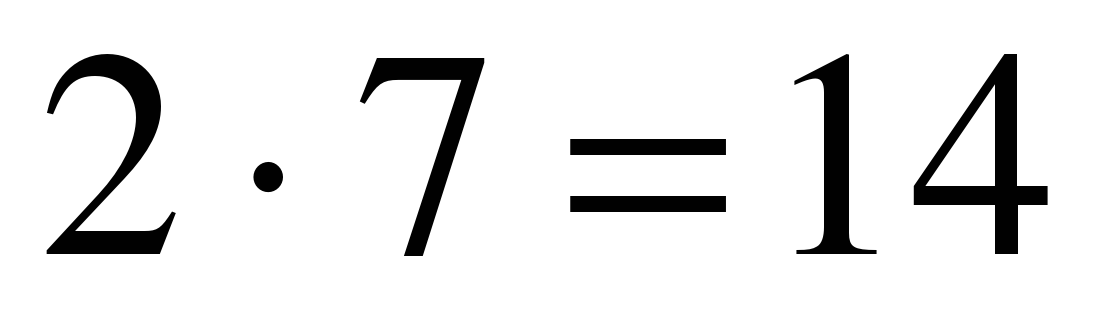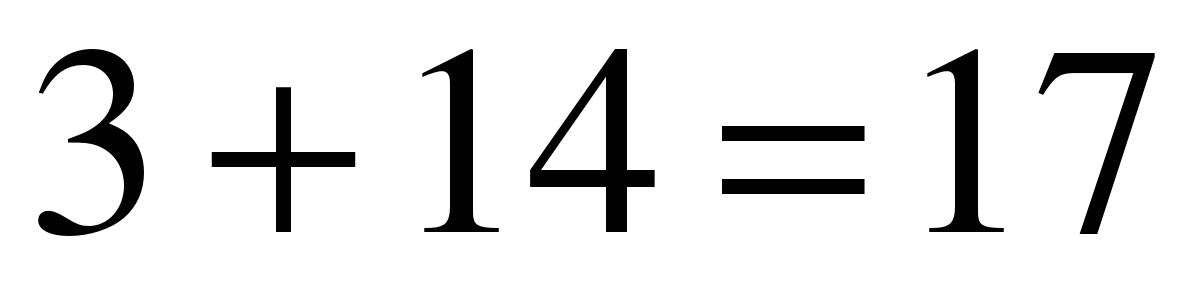, , ; 7 – предпоследняя цифра результата, 1 запоминаем;
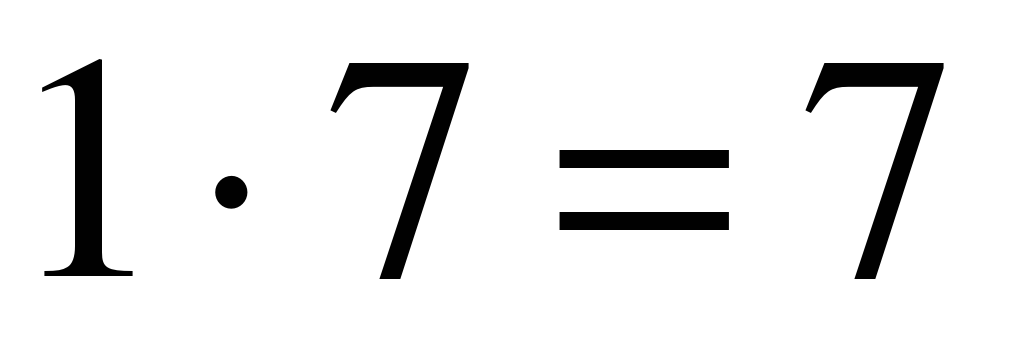, да ещё удержанная в уме цифра 1, имеем 8 – первая цифра результата, т.е. .

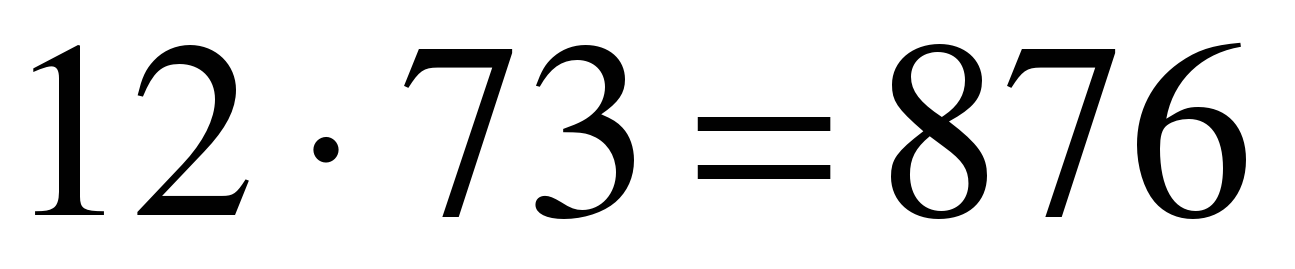Далее, к полученному числу приписываем нуль, т.е. .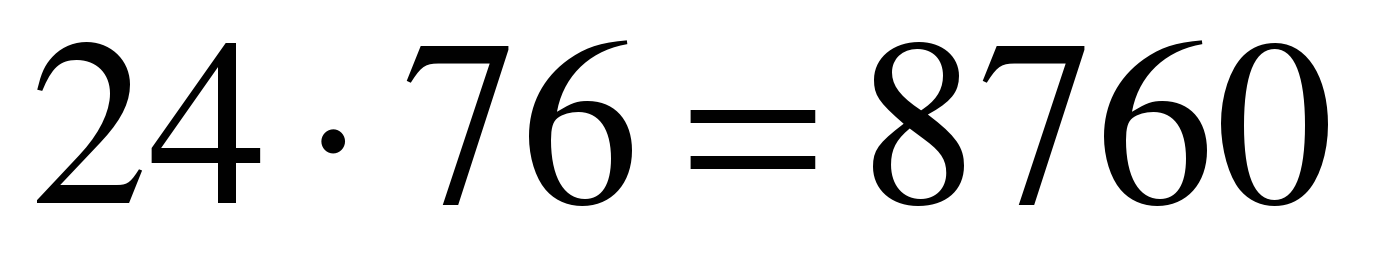

Ответ: 8760.

Поправка в несколько дней, происходящая от високосных лет, обыкновенно в расчет не принимается, хотя её легко ввести, прибавив к результату четверть числа лет, – в нашем примере 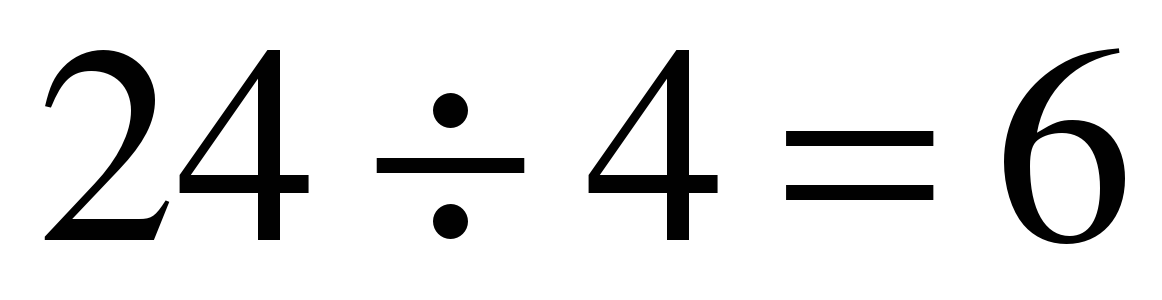; общий результат, следовательно, 8766.

«КАКОЙ ДЕНЬ НЕДЕЛИ?»

Умение быстро определять день недели, на какой приходится та или иная дата (например, 17 января 1893г., 4 сентября 1943г. и т.п.), основано на знании особенностей нашего календаря [4, с. 138].

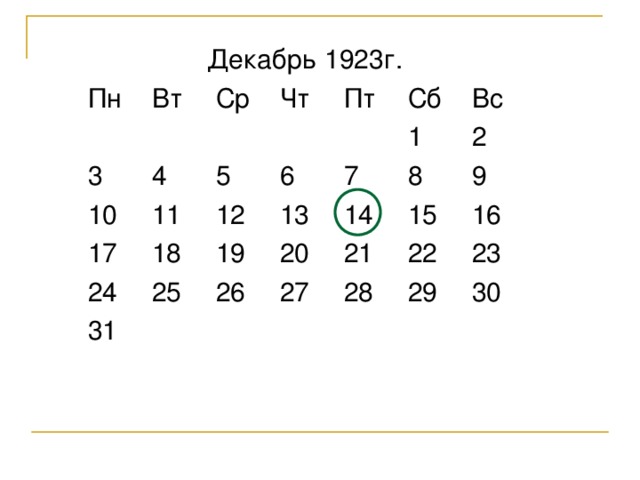
Пример. Найти день недели, на который приходится 14 декабря 1923г.

Решение.

1 способ: 1-е января 1г. нашей эры приходилось (установлено расчетом) на субботу. Т.к. в каждом простом году 365 дней, или 52 полных недели и 1 день, то год должен кончатся тем же днем недели, каким начался. Поэтому следующий год начинается одним днем недели позже, чем предыдущий. Если 1-е января 1г. была суббота, то 1-е января 2г. было днем позже, т.е. воскресенье. 1-е января 1923г. было бы на 1922 дня (1923-1) после субботы, – если бы не было ни одного високосного года. Число високосных лет мы найдем, разделив 1923 на 4, получим 480; но отсюда, для нового стиля, надо исключить календарную разницу в 13 дней: 480-13=467. К полученному числу надо прибавить число дней, протекающих после 1-го января 1923г. до определяемой даты – до 14 декабря, что составит 347 дней. Сложив 1922, 467 и 347, мы делим сумму на 7, и по полученному остатку о определяем, что 14 декабря 1923г. приходилось на 6-й дней после субботы, – а именно в пятницу.

Ответ: пятница.

2 способ: Прежде всего заметим, что в течение каждого 28-летнего периода бывает, вообще говоря, 7 високосных лет (неделя), – так, что каждые 28 лет день недели любой даты должен повторяться. Кроме того вспомним, что в предыдущем примере мы вычли из 1923 сначала 1, а затем календарную разницу обоих стилей, т.е. 13, всего 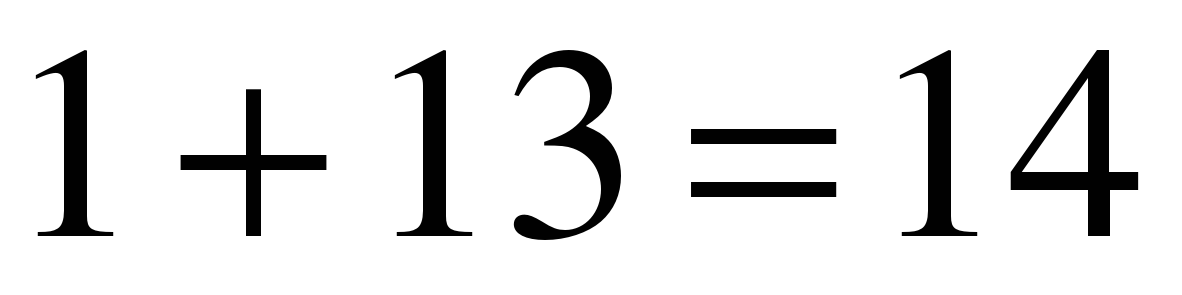дней, или две полных недели. Но полное число недель, понятно, не влияет на результат. Поэтому для дат XX в. надо принимать во внимание только:

1) число дней, протекших с 1 января данного года – в нашем примере 347;

2) прибавить число дней, соответствующее остатку лет от деления 1923 на 28, т.е. 19;

3) число високосных лет в этом остатке – 4.

Сумма этих трех чисел 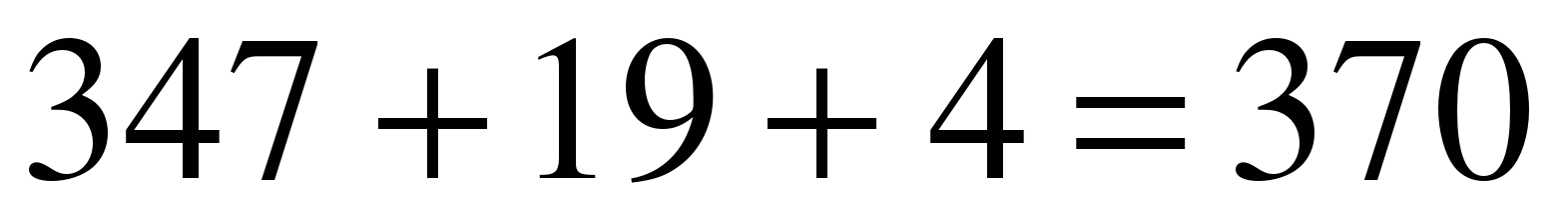, дает при делении на 7 тот же остаток 6, который был получен нами раньше, значит, исходный день – пятница.

Ответ: пятница.

Дальнейшее упрощение состоит в том, что вместо полного числа дней месяца (при исчислении числа дней, протекших после 1-го января заданного года), принимают в расчет его остаток от деления на 7. Далее, разделив 1900 на 28, получаем в остатке 24 гг., в которых содержится 5 високосных лет. Прибавив их к 24-м и найдя, что сумма 24+5=29 дает при делении на 7 остаток 1, определяем, что 1 января 1900г. было в 1-й день недели. Отсюда для первых чисел каждого месяца получаем соответствующие им дни недели (мы будем их называть «остаточными числами», табл. 1).

Таблица 1

«Остаточные числа» месяца

(1900-1999 гг.)

Январь	1
Февраль	4
Март	4
Апрель	0
Май	2
Июнь	5
Июль	0
Август	3
Сентябрь	6
Октябрь	1
Ноябрь	4
Декабрь	6

Для дат предшествующих столетий (XIX, XVIII и т.д.) можно пользоваться теми числами, но надо помнить, что в XIX веке разница между новым и старым стилем была не 13, а 12. Кроме того, при делении 1800 на 28 получается в остатке 8, что вместе с 2 високосными годами в этом остатке составляет 10 (или 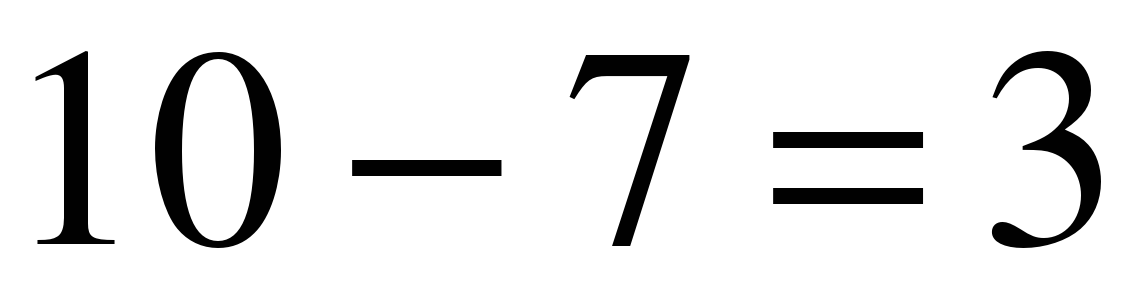), т.е. соответствующее характерное число для дат XIX в должно быть увеличено на 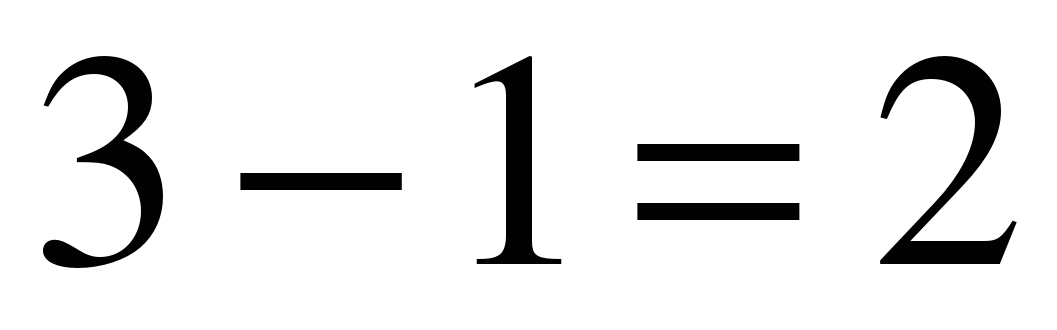. Например, день недели 31 декабря 1864 г нового стиля мы определим сначала по предыдущему, а затем внесем поправку – прибавим 2 дня.

Число месяца……………………31

Остаточное число для декабря…6

Сначала столетия прошло лет….64

В том числе високосных………..16

Поправка для XIX в……………..2

Сумма 119

Остаток от деления на 7 – 0, значит 31 декабря 1864 г – суббота.

Ответ: суббота.

Технология деятельностного подхода при решении задач календаря

Рассмотрим реализацию деятельностного подхода на примере решения следующей задачи.

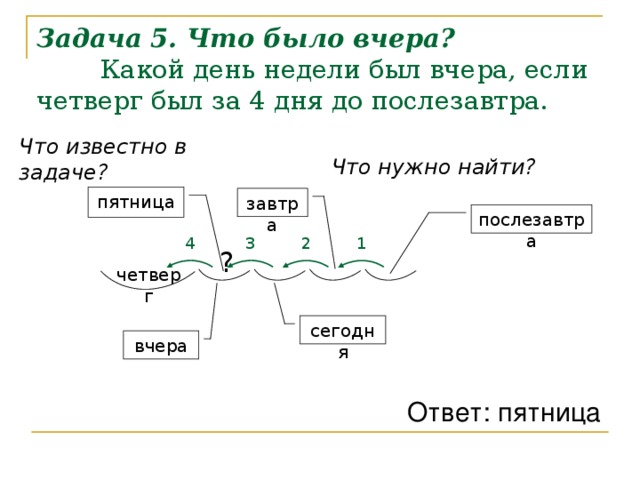
Задача 1. Что было вчера?

Какой день недели был вчера, если четверг был за 4 дня до послезавтра.

Действие 1. ИЗУЧЕНИЕ СТРУКТУРЫ ЗАДАЧИ

Учитель демонстрирует вопросы, которые следует задавать при изучении текста задачи:

какие объекты фигурируют в тексте задачи (дни недели);
что известно в тексте задачи (четверг был за 4 дня до послезавтра);
что нужно найти (день недели, который был вчера).

Решение. Построение модели: обозначим через 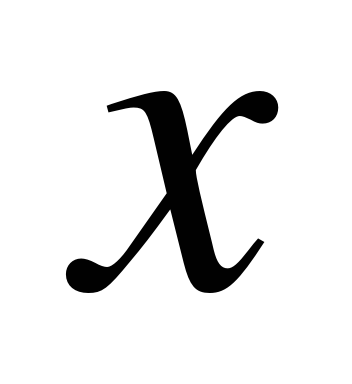– тот день недели, который нужно найти и обозначим его на модели.

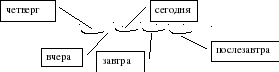
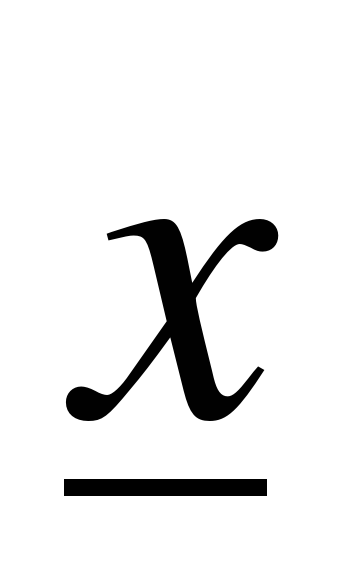
Ответ: пятница.

Краткая схематическая запись

Четверг

Вчера –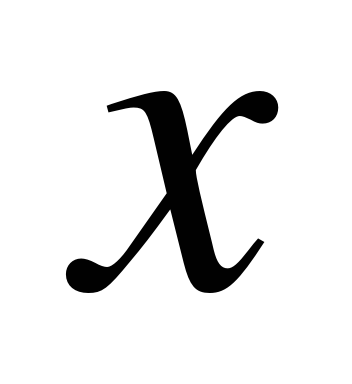

Сегодня за 4 дня

Завтра

Послезавтра

Действие 2. ПОИСК ПЛАНА РЕШЕНИЯ ЗАДАЧИ

Анализ;

Синтез.

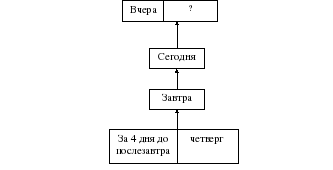
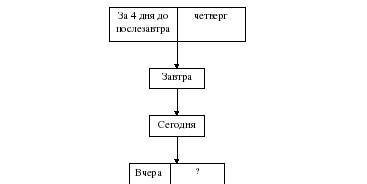
Выстраивается план решения:

Отсчитать 4 дня до послезавтра;
Найти день, который был вчера.

Действие 3. ОСУЩЕСТВЛЕНИЕ ПЛАНА РЕШЕНИЯ

Оформляем решение задачи согласно плана её решения.

Решение:

Отсчитывая 4 дня до послезавтра находим, что четверг находится перед днем, который был вчера (см. с. 17).
День, который идет вслед за четвергом – пятница, значит пятница – искомый день.

Действие 4. ПРОВЕРКА РЕШЕНИЯ ЗАДАЧИ

Проверим правильность решения нашей задачи: т.к. вчера – пятница, тогда сегодня – суббота, завтра – воскресенье, послезавтра – понедельник и за 4 дня до понедельника – пятница. Значит решение правильное.

Действие 5. ИЗУЧЕНИЕ РЕШЕНИЯ ЗАДАЧИ

Осмысление ответа и его полная запись:

Ответ: день, который был вчера – пятница.

Завершая работу над задачей, учащиеся ещё раз прочитывают её, просматривают решение. Пытаются сами составить аналогичные задачи, решить по структуре данной задачи.

Локальная система задач

28 дней [3].

Сколько месяцев в году имеют 28 дней?

Ответ: Все 12, т.к. если в месяце 30 дней, то и 28 среди них есть.

Пять дней [3].

Назовите пять дней, не называя чисел (напр., 1, 2, 3,..) и названий дней (напр., понедельник, вторник, среда...).

Ответ: Позавчера, вчера, сегодня, завтра, послезавтра.

Что это за день? [3]

Если этот день не идет вслед за понедельником и не перед четвергом, а завтра не воскресенье и вчера было не воскресенье, а послезавтра будет не суббота и позавчера была не среда, то что это за день?

Ответ: Воскресенье.

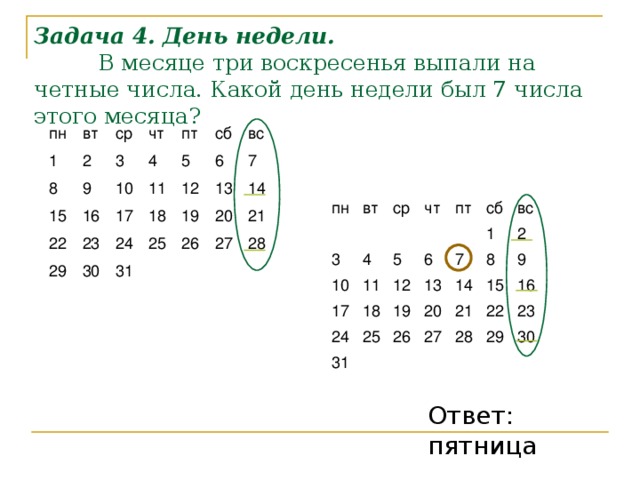
День недели [3].

В месяце три воскресенья выпали на четные числа. Какой день недели был седьмого числа этого месяца?

Решение. Через семь дней повторяется каждый день недели. Первые 28 дней содержат четыре понедельника и т.д. и четыре воскресенья. Причем, два воскресенья выпадают на четные числа, а два - на нечетные. Значит, третье воскресенье выпадает на 30 число. Таким образом, 2-го числа также было воскресенье, а 7-го числа – пятница.

Ответ: пятница.

Три пятницы [3].

Три пятницы некоторого месяца пришлись на четные даты. Какой день недели был 18 числа этого месяца?

Решение. Через семь дней повторяется каждый день недели. Первые 28 дней содержат четыре понедельника и т.д. и четыре воскресенья. Причем, две пятницы выпадают на четные числа, а две – на нечетные. Значит, третья пятница выпадает на 30 число. Таким образом, 16-го числа также была пятница, а 18-го числа – воскресенье.

Ответ: Воскресенье.

Что было вчера? [3]

Какой день недели был вчера, если четверг был за 4 дня до послезавтра.

Ответ: вчера была пятница.

Найти день недели, на который приходится 14 декабря 1923г [4, с. 139].

Решение.

Число месяца – 14

Остаточное число для декабря – 6 (см.с.16)

С начала столетия прошло лет – 23

В том числе високосных – 5

Сумма 48

Остаток от деления на 7 – 6, значит 14 декабря 1923г – пятница.

Ответ: пятница.

Найти день недели, на который приходится 29 февраля 1912г [4, с. 142].

Решение.

Число месяца – 29

Остаточное число для февраля – 4 (см.с.16)

С начала столетия прошло лет – 12

В том числе високосных^¹ – 2

Сумма 47

Остаток от деления на 7 – 5, значит 29 февраля 1912г – четверг.

Ответ. четверг.

Найти день недели, на который приходится 31 марта 1923г [4, с. 141].

Решение.

Число месяца – 31

Остаточное число для марта – 4 (см.с.16)

С начала столетия прошло лет – 23

В том числе високосных – 5

Сумма 63

Остаток от деления на 7 – 0, значит 31 марта 1923г – суббота.

Ответ: суббота.

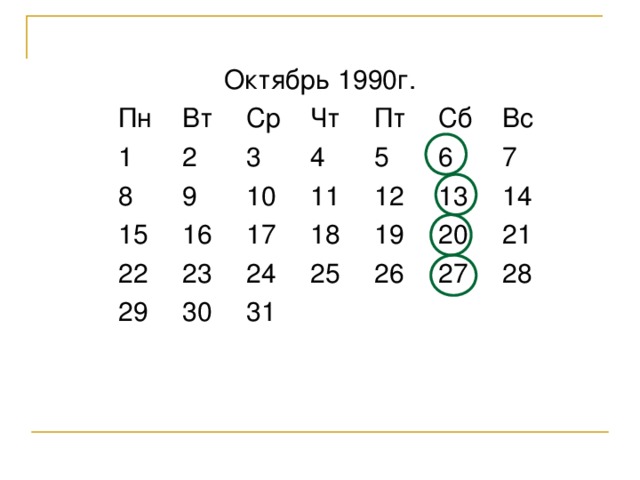
Найти числа месяца, зная день недели, месяц и год:

суббота октября 1990г.;

Решение. Число месяца –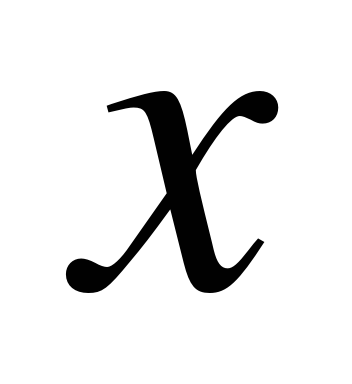

Остаточное число для октября – 1 (см.с.16)

С начала столетия прошло лет – 90

В том числе високосных – 22

Сумма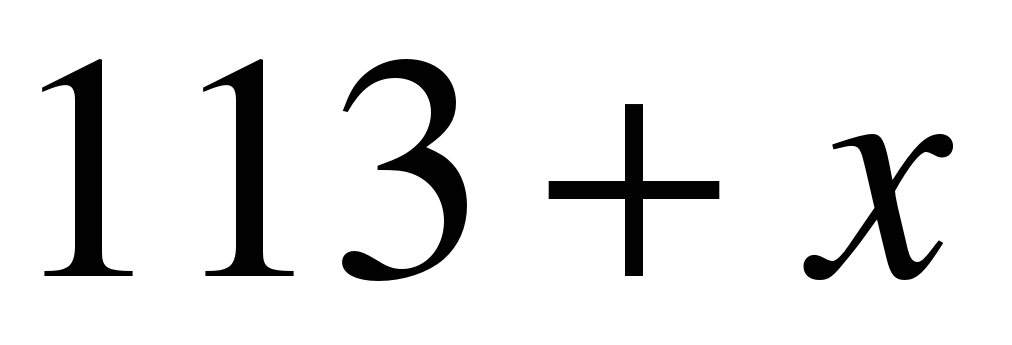

Т.к. дано, что день недели – суббота, тогда остаток от деления на 7 будет 0. Значит значение 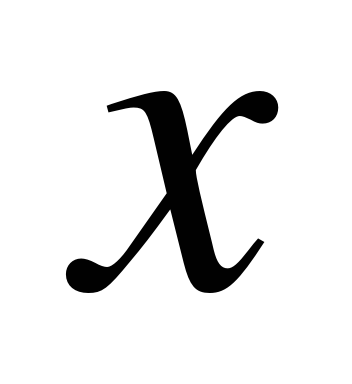подбираем так, чтобы сумма 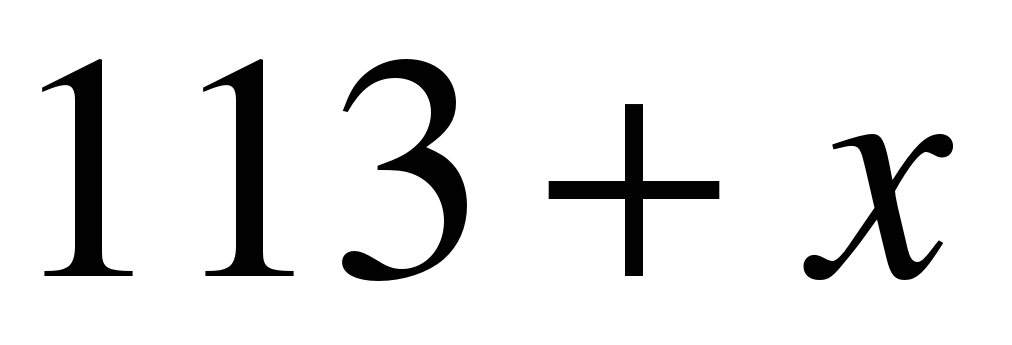нацело делилась на 7.Самое наименьшее 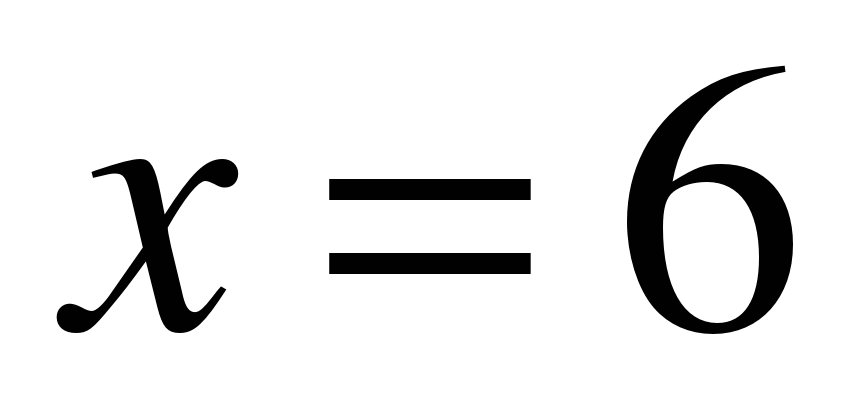. Далее находим остальные числа месяца: 13, 20, 27.

Ответ: 6, 13, 20, 27.

вторник октября 1969г..

Решение. Число месяца –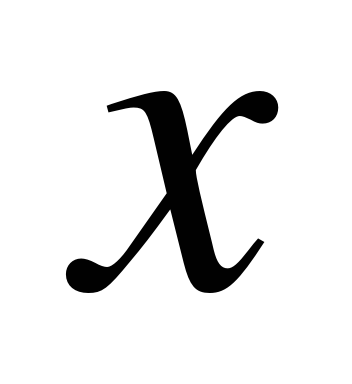

Остаточное число для октября – 1 (см.с.16)

С начала столетия прошло лет – 69

В том числе високосных – 17

Сумма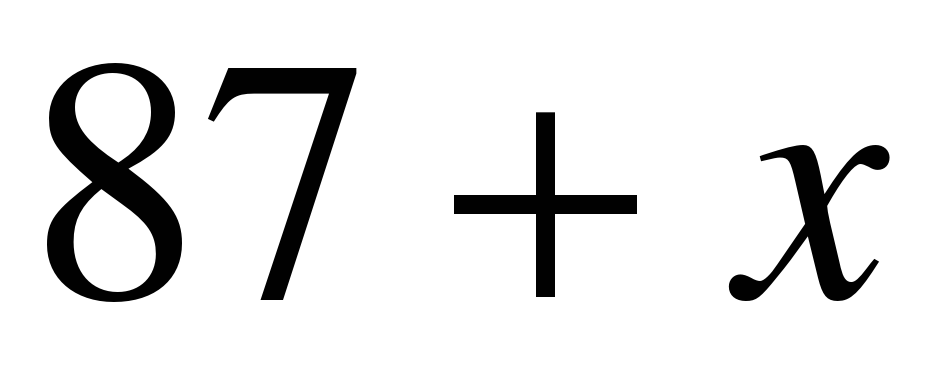

Т.к. дано, что день недели – вторник, тогда остаток от деления на 7 будет 3. Значит значение 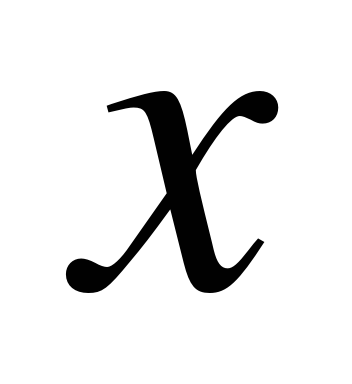подбираем так, чтобы сумма 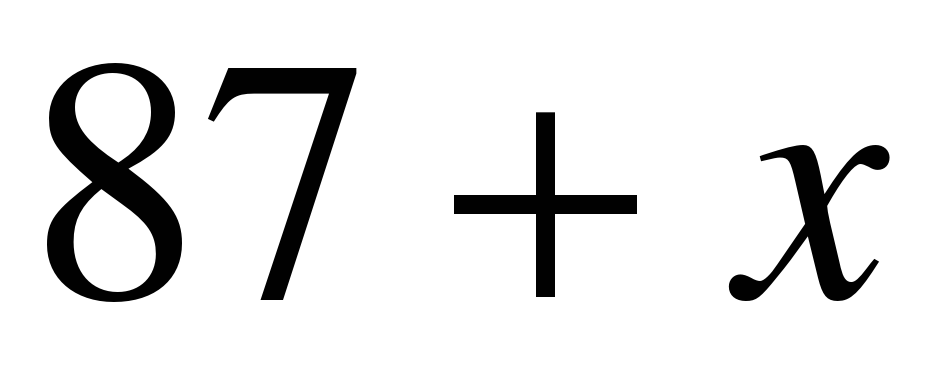делилась на 7 с остатком 3. Самое наименьшее 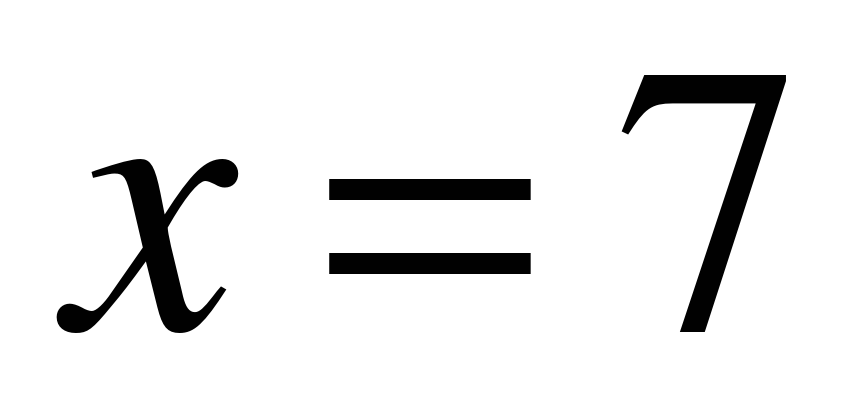. Далее находим остальные числа месяца: 14, 21, 28.

Ответ: 7, 14, 21, 28.

1 Принято во внимание, что один високосный год уже был учтен, когда мы взяли дату 29 февраля. Поэтому пишем не 3 високосных года, а 3.

Просмотр содержимого документа
«Раздаточный материал»

«Остаточные числа месяца»

Январь	1
Февраль	4
Март	4
Апрель	0
Май	2
Июнь	5
Июль	0
Август	3
Сентябрь	6
Октябрь	1
Ноябрь	4
Декабрь	6

(1900-1999)

1-е января 1г. была суббота.

Январь	1
Февраль	4
Март	4
Апрель	0
Май	2
Июнь	5
Июль	0
Август	3
Сентябрь	6
Октябрь	1
Ноябрь	4
Декабрь	6

«Остаточные числа месяца»

(1900-1999)

1-е января 1г. была суббота.

Просмотр содержимого презентации
«Задачи календаря»

Задачи календаря

Задача 1. Пять дней. Назовите пять дней, не называя чисел (например, 1, 2, 3,..) и названий дней (например, понедельник, вторник, среда,..).

Задача 2. 28 дней. Сколько месяцев в году имеют 28 дней?

Задача 3. Что это за день? Если этот день не идет вслед за понедельником и не перед четвергом, а завтра не воскресенье и вчера было не воскресенье, а послезавтра будет не суббота и позавчера была не среда, то что это за день?

пн вт ср чт пт сб вс