Семёркина Ольга Николаевна
Математика 3 класс
Тема: Числовой луч
Система Л. В. Занкова
И. И. Аргинская, Е. И. Ивановская. Математика: учебник для 3 класса - Самара: Корпорация «Фёдоров», Издательство «Учебная литература»
Учитель: Семёркина Ольга Николаевна, МБОУ СОШ №20, о. Муром, Владимирской области
Задачи урока:
предметные
дать понятие о единичном отрезке и его величине на числовом луче;
развивать умение решать задачи без соотнесения с ранее знакомыми;
развивать геометрические представления при решении задач на нахождение расстояния;
развивать творческое математическое мышление посредством введения эвристических вопросов;
рассмотреть несколько вариантов решения задачи;
расширить знания по окружающему миру и стимулировать к поиску новых знаний.
метапредметные:
формировать УУД:
интерес к новому учебному материалу,
основы гражданской идентичности личности в форме осознания «Я» как гражданин России,
воспитание интереса к предмету через познание родного края,
воспитание интереса к путешествию по родному краю,
умение учитывать выделенные учителем ориентиры действия в новом учебном материале,
умение ориентироваться в разнообразии способов решения задачи,
умение формулировать собственное мнение, контролировать действия партнёра,
развитие мышления через умение сравнивать, анализировать и обобщать полученные результаты.
Слайд № 3 Создание учебной мотивации.
Учитель:
- Здравствуйте, тихо сели! Урок математики! А пройдёт он у нас сегодня необычно.
Вначале мне хотелось бы узнать, а кто из вас любит путешествия? (Конечно, все!)
Учитель
- И сегодня мы отправимся в путешествие по необъятным просторам нашей великой страны, которая называется ….. РОССИЯ.
- Ребята, а чтобы быть обычным или успешным путешественником, мы должны к нему хорошо подготовиться. В этом нам помогут многие уроки математики, в том числе и этот урок.
- Открываем тетрадь – это на сегодня маршрутный лист нашего путешествия. Записываем число, классная работа. Итак, мы отправляемся в путь 26 января.
Запись числа классной работы.
Слайд № 4
Учитель:
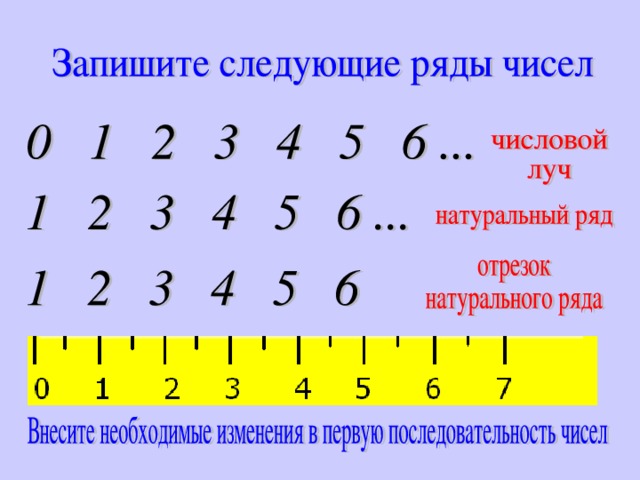
- Внимание на экран. Перед вами 3 последовательности чисел.
1. Повторение знаний об отрезке и натуральном ряде чисел
0 1 2 3 4 5 6 …
1 2 3 4 5 6 7 ….
1 2 3 4 5 6 7
Учитель. Запишите эти последовательности чисел
- Что вы можете о них сказать?
Задается «общий» вопрос, который избавляет учителя от многовопросия и позволяет учащимся наиболее полно высказаться об объектах.
Дети. №1 – числовой ряд, потому что начинается с 0 ,
№ 2 – натуральный ряд чисел,
№ 3 – отрезок натурального ряда чисел
Запись № 1 используют для измерения длины, такая числовая последовательность – на линейке, если добавить наименования
Учитель. Внесите необходимые изменения в 1 ряд чисел.
(Дети самостоятельно работают в тетради).
Последующая проверка.
Слайд № 5
На слайде представлены все варианты выполнения задания
Учитель. Как можно назвать эти записи?
Дети. Единицы измерения длины. Линейные единицы измерений.
Учитель. Подумайте, какие задания будут на уроке?
Дети.
переводить одни измерения в другие.
Решать задачи с такими величинами.
Находить города и дороги на карте.
Учитель. (Сообщение для учащихся темы и целей урока).
Мы будем строить числовой луч и на нем будем обозначать величины;
решать задачи с помощью числового луча простые и более сложные.
вернемся к решению задачи на нахождение расстояния между деревнями и решим её другим способом.
И, конечно, будем знакомиться с новыми знаниями об окружающем мире, как настоящие путешественники.
Слайд № 6.
Повторение материала прошлого урока и введения нового понятия (на материале № 293 учебника)
Учитель.
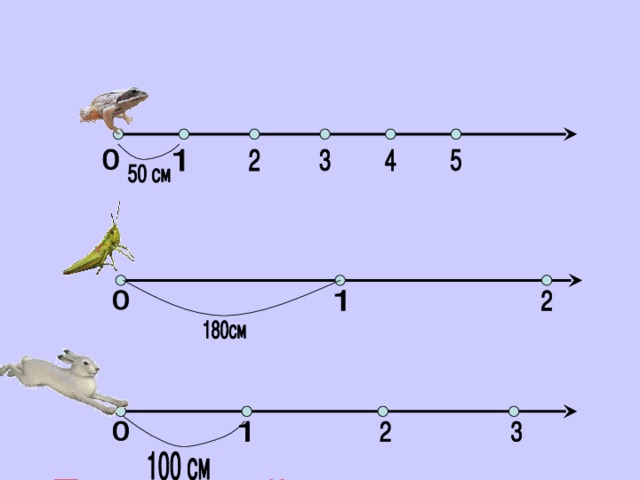
- Внимание на экран. Рассмотрите рисунок. Что вы можете сказать?
Дети.
Это луч, и на нем точки на одинаковом расстоянии друг от друга.
Лягушка прыгает одинаковыми прыжками.
Учитель
- Кто видел, как прыгает лягушка? Мы вместе сможем это увидеть в электронном пособии «Коллекция фото и видеоизображений. Биология»
Что показывают числа 1 2 3?
Дети. Количество прыжков лягушки.
Учитель Какое число надо поставить у начала луча?
Дети. .0, потому что это начало первого прыжка
Учитель Рассмотрите следующий рисунок. Что вы можете сказать?
Дети
Это луч, и на нем точки на одинаковом расстоянии друг от друга.
Кузнечик прыгает одинаковыми прыжками.
Каждый прыжок больше прыжка лягушки
В начале луча должен стоять 0
Учитель Что вы можете сказать о третьем рисунке?
Это тоже луч, и на нем точки тоже на одинаковом расстоянии друг от друга,
Заяц прыгает одинаковыми прыжками, большими, чем у лягушки, но меньшими, чем у кузнечика.
Учитель Что напоминают эти лучи?
Дети Линейки с разными мерками.
Учитель
- Больше об этих животных мы узнаем на уроке окружающего мира, а поможет нам в этом электронная энциклопедия Кирилл и Мефодий.
- Все ли животные сделали одинаковое кол-во прыжков? Если нет, то почему?
Дети Нет, разная длина прыжка
Учитель – А знаете ли вы длину прыжка каждого животного?
- Выберите из предложенных мерок мерку для каждого животного
(На доске 100см, 50 см; 180 см)
Учитель. Мерка, которая выбрана вами для каждого животного, называется единичным отрезком. (Появление на слайде этого построения)
Слайд № 7. Устный счет
Учитель. Рассмотрите эти математические ситуации и предложите одноклассникам свои вопросы.
Дети. Найдите расстояние, которое пропрыгала лягушка?
50х5=250(см) (250 см=25дм)
Учитель. Как узнали? Запишите в тетради полученную величину и переведите ее в более крупные единицы измерения.
Дети Какова длина всех прыжков кузнечика? 180х2=360 (см) (360см)
Учитель Как узнали? Выполните в тетради операцию перевода в более крупные единицы
Дети Какое расстояние пробежал заяц? 100х3=300(см) (300 см)
Учитель Как узнали? Переведите эту величину в дм
Дети .На ск. меньше прыжок лягушки, чем прыжок кузнечика? 180-50=130 (см) На 130 см
Дети Во ск. раз больше прыжок зайца, чем лягушки? 100:50=2 (раза) (В 2 раза)
Итог 1 этапа.
Учитель Кратко расскажите, что мы сейчас делали, что нового узнали?
Дети
Строили числовые лучи и узнали про единичный отрезок.
Решали задачи, находили расстояние нескольких прыжков и разницу величины прыжков.
Слайд № 8.
ФИЗМИНУТКА
Учитель проговаривает команды для движений, которые должны показать дети, а сам может выполнять другие движения. Команды: воздух (руки вверху), вода (руки впереди), огонь (руки крутим перед собой), земля (руки вниз).
Слайд № 9.
Справка: на прошлом и этом уроке дети впервые знакомятся с геометрическим представлением расположения объектов, чтобы найти расстояние. Прием возвращение к ранее решенной задаче – отличительная особенность методики в системе Л. В. Занкова. В данном случае это нужно для поиска нового варианта решения задачи.
Кроме этого, детям предлагается еще один «готовый» ответ задачи, который вносит противоречие в наше решение (одно из свойств системы - коллизии). Эту ситуацию мы рассматриваем и убеждаемся, что условие позволяет получить еще одно решение задачи.
Возвращение к решенной задаче на прошлом уроке.
Учитель: Переходим к решению задач.
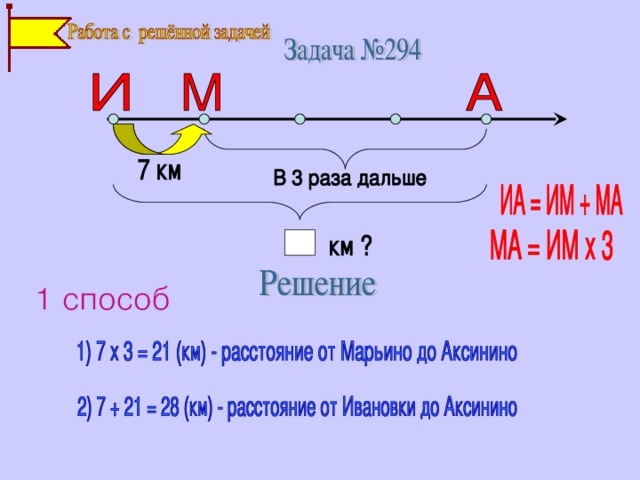
Задача № 294 (текст из учебника)
Деревни Ивановка, Марьино и Аксинино расположены на одной дороге. От Ивановки до Марьино 7 км, а от Марьино до Аксинино в 3 раза дальше. Сколько км от Ивановки до Аксинино?
Учитель Как вы поняли условие задачи, что деревни находятся на одной дороге?
Переведите текстовую информацию в графическую.
Как геометрически представили эту дорогу на чертеже?
Дети (пошаговое восстановление предыдущей работы). Задача решена на предыдущем уроке.
Обозначили буквами И – Ивановку, затем М – Марьино, А – Аксинино по порядку –слева-направо.
Написали данные; 7 км, «в 3 раза дальше»
Объединили скобкой расстояние от Ивановки до Аксинино, которое надо найти.
Учитель Что вы можете сказать о единичном отрезке?
Дети Единичный отрезок – 7 км. Потом он повторяется 3 раза
Учитель Расскажите план решения по буквенным выражениям
Дети Надо найти расстояние ИА которое состоит из ИМ и МА. Это сумма расстояний. Нам известно, что ИМ – 7 км. МА можно найти, т.к. это расстояние в 3 раза дальше, чем ИМ, значит, ИМх3.
(Проверка оформления решения по щелчку мыши).
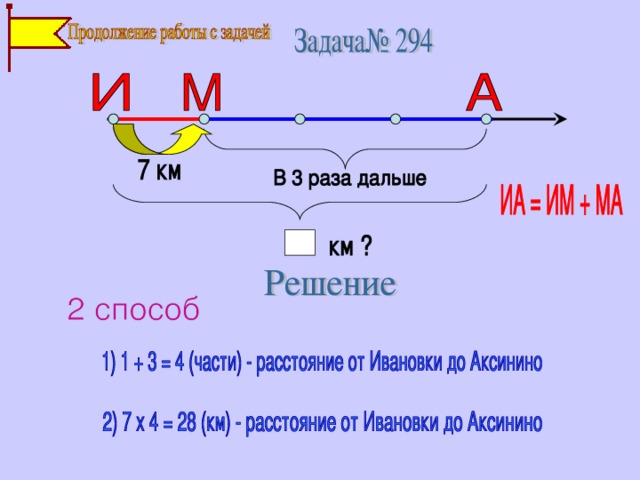
Слайд № 10. « В зоне ближайшего развития» . Повышенный уровень трудности. Это решение спланировано учителем. Такой способ решения в учебниках появится гораздо позже. Но эта пропедевтическая работа поможет решать задачи из следующей темы «Дробные числа».
Учитель А теперь попробуем решить эту задачу другим способом.
Выполните построение числового луча, как мы с вами только что повторили (алгоритм на листе) – комментирование????
Назовите искомое расстояние
Дети От Ивановки до Аксинино (ИА)
Учитель Рассмотрим составляющие это расстояние отрезки.
Дети Единичный отрезок и еще 3 таких же отрезка от Марьино до Аксинино
Учитель Вспомните начало урока, как мы решали задачи про прыжки животных.
Как можно представить это расстояние?
Дети Как 4 прыжка
Как 4 отрезка
1+3 = 4
Учитель Найдите искомое расстояние, используйте знакомый уже способ нахождения расстояния прыжков животных.
Выполните запись решения самостоятельно. Индивидуальная помощь
(Проверка с появлением слайдов по щелчку мыши)
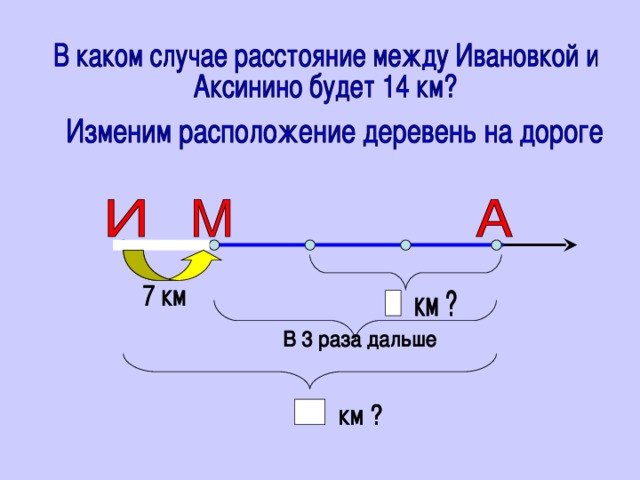
Слайд № 11. (по пункту № 3 этой задачи) Возникновение противоречия
Учитель Внимание на экран. При решении этой задачи Костя получил ответ 28 км, а Вася – 14 км. Что вы скажете об ответах мальчиков?
Дети Ответ Кости – 28 км как у нас, а ответ Васи, наверное, неправильный.
Учитель Кто считает, что ответ Васи неверный?
Учитель Давайте исследуем эту ситуацию и разрешим проблему. Сравните эти расстояния.
Слайд № 12.
Второе решение задачи, связанное с неполным условием о расположении объектов
Дети 14 км в 2 раза меньше, чем 28 км
Учитель Как так может быть? Посмотрите на наш чертеж, может быть можно его изменить?
Дети Надо поставить Ивановку в середину
Поставить Ивановку на расстоянии 2 отрезков от Аксинино
(по щелчку мыши выполняется это действие).
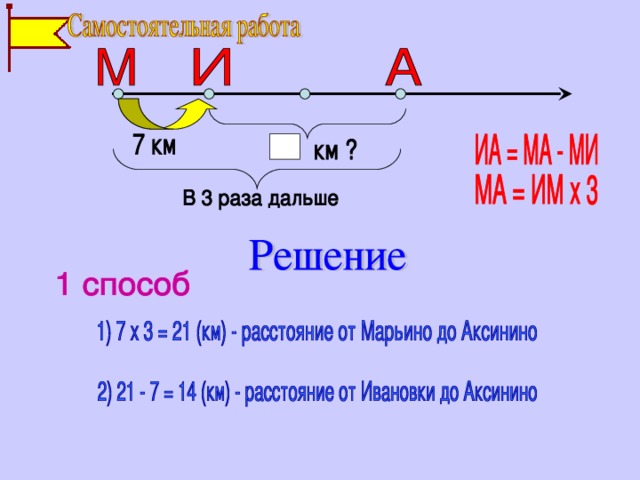
Учитель Назовите искомое расстояние
Дети От Ивановки до Аксинино (ИА).
Учитель Назовите данные
Дети Расстояние от Марьино до Ивановки 7 км
Это единичный отрезок
Расстояние от Марьино до Аксинино – в 3 раза дальше (МИ взять 3 раза)
Учитель Как найти искомое расстояние (ИА)
Дети Надо из всего расстояния вычесть МИ (от Марьино до Аксинино)
Выполнение решения (Появление решения на слайде. «Сильные» учащиеся решали самостоятельно)
Слайд № 13. Самостоятельная работа.
Оказание индивидуальной помощи 5 учащимся. Чертеж для решения показать.
Действие по щелчку мыши для проверки решения
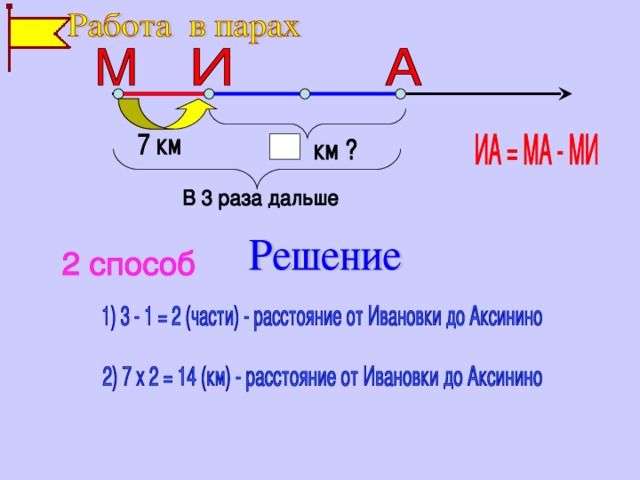
Слайд № 14. (работа в парах)
Учитель Можно ли решить эту задачу, представив расстояние в частях, как мы решили предыдущую вторым способом?
Можно советоваться, решать в парах, обернуться к следующей паре, но помни правила дружной работы:
(проверка решения по щелчку мыши на слайде)
Учитель Все ли убедились в том, что так же верен ответ 14 км?
Дети (Да – ответ жестом согласия - рука).
Д.М. Контроль и самоконтроль
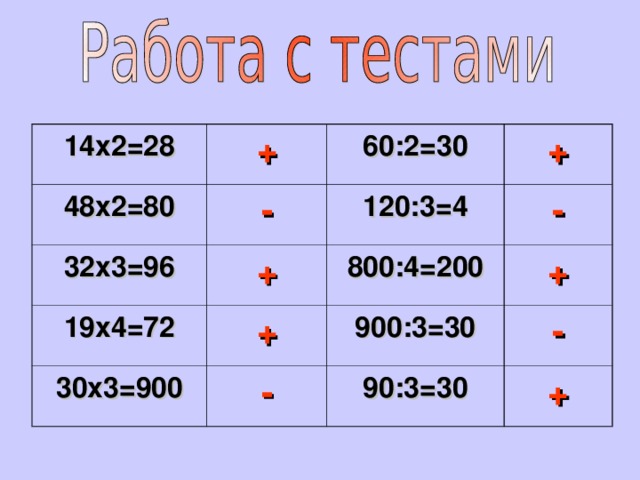
Работа с тестами.
– Ну а теперь пришло время проверить, как вы усвоили тему предыдущих уроков. Перед вами лежат листочки, в которых выполнено внетабличное умножение и деление. Ваша задача, проверить правильность выполненных действий. Если задание выполнено верно, то рядом, в пустой клеточке, вы ставите “+”, а если неверно, то ставите знак “–”.
| 14х2=28 |
| 60:2=30 |
|
| 48х2=80 |
| 120:3=4 |
|
| 32х3=96 |
| 800:4=200 |
|
| 19х4=72 |
| 900:3=30 |
|
| 30х3=900 |
| 90:3=30 |
|
– Вижу, что вы справились с заданием. А сейчас поменяйтесь листочками друг с другом для взаимопроверки. У меня на доске даны ответы. Сверьте их с теми, которые получились у вас и оцените своего товарища.
Подведение итогов:
Итак, урок подошёл к концу.
Слайд № 15 .Применение знаний в окружающем мире
Учитель Где нам пригодятся знания о расположении населенных пунктов, о нахождении расстояния?
Дети Когда едем на машине, надо знать, сколько километров между городами
Надо знать расстояние, чтобы хватило бензина до заправки.
Какая дорога короче, какая длиннее.
Нужно уметь находить расстояния по карте.
Слайд № 16. Домашнее задание
Построй числовой луч. (Помощь в № 293-6).
2. Задача № 294 Выбери вариант выполнения:
А) составь и реши подобную задачу;
Б) составь обратную задачу
В) Какое уточнение нужно внести в задачу, чтобы у неё было только одно решение (№ 294, пункт5)
Учитель:
- Мне сегодня было очень комфортно с вами на уроке. Спасибо вам.
Продолжи фразу:
Я узнал (а) …
Я повторил (а) …
Я научился (лась) …
Рефлексия.
- Ну, а теперь мне хотелось бы узнать, как вы сами оцениваете свою работу на уроке. У каждого из вас, на парте, лежит пассажир, ожидающий поезд. Но это необычный поезд. У него разные вагоны: веселые-красные и грустные-синие. Вы должны посадить своего пассажира в тот вагон, который соответствует вашему настроению от сегодняшнего урока.
7





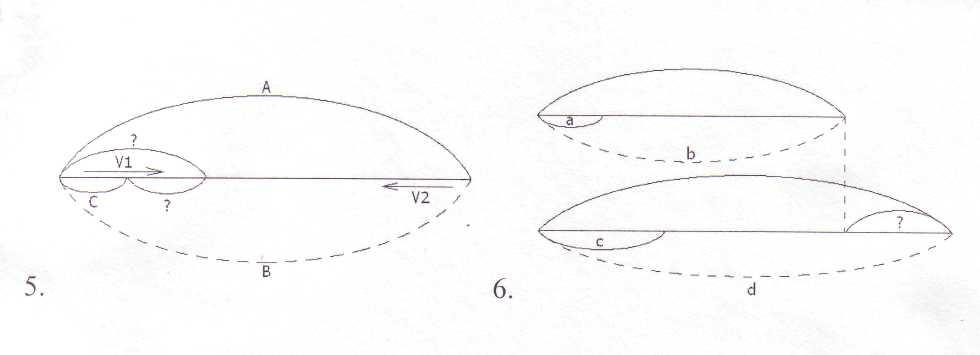 0.В первом гараже было 8 машин. Когда из него во второй гараж переехали две машины, в гаражах стало машин поровну. Сколько машин было во втором гараже?
0.В первом гараже было 8 машин. Когда из него во второй гараж переехали две машины, в гаражах стало машин поровну. Сколько машин было во втором гараже?