Батыс Қазақстан облысы
Теректі ауданы
Подстепный қазақ жалпы орта білім беретін мектептің
Математика -физика пәнінің І санатты мұғалімі
Избасова Мариям Файзуллақызы
Тақырыбы: Бір айнымалысы бар сызықтық тенсіздікті шешу.
Сабақтын мақсаты:
Білімділік: ахв немесе ах
жиының сан аралығымен жазып дағдылану
Дамытушылық: Оқушылардың жана білімді менгеруге,білімін қолданып
ойлау қабілетің,есептеу қабілетінің артуына дағдыландыру
Тәрбиелік: Білімді менгеруде жүйелі түрде жұмыс істеуге ,өз ойын дәл,
нақты айта білуге тәрбиелеу
Сабақтын түрі: Жана білімді менгеру
Әдісі : Сұрақ-жауап (СТО технологиясының элементтері)
Көрнекілікі:Компьютер,видео-проектор,семантикалық карта,слайдпен жұмыс
1.Қызығушылығын ояту

 Санды тенсіздік І
Санды тенсіздік І
С
 анды тенсіздіктерді қосу Санды тенсіздіктерді көбейту
анды тенсіздіктерді қосу Санды тенсіздіктерді көбейту
Санды тенсіздіктерді азайту Санды тенсіздіктерді бөлу
2
Сан аралықтары
.Мағынаны таныту


 а в
а в
1. 3 2. -2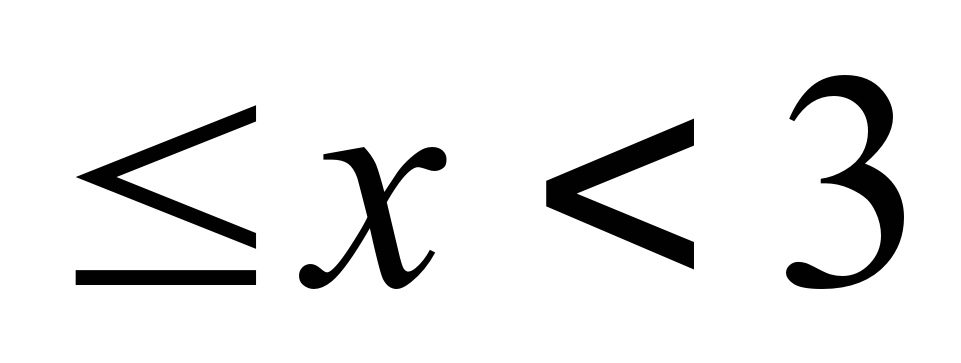 3. х
3. х





 //////////////// ///////////// ////////////////
//////////////// ///////////// ////////////////

 3 8 -2 3 5
3 8 -2 3 5
Интервал Жартылай интервал Ашық сәуле
(3;8) белгіленуі [-2;3) (- ;5)
;5)
Бір айнымалысы бар теңсіздіктер ах в немесе ах в
Бір айнымалысы бар сызықтық теңсіздіктер. Мұндағы а,в – қандай да бір сандар. х-айнымалы, в- бос мүше.
Бір айнымалысы бар теңсіздіктің шешімі деп, айнымалының теңсіздікті тура санды теңсіздікке айналдыратын мәнін айтады.
Теңсіздікті шешу дегеніміз- оның барлық шешімдер жиынын табу немесе шешімдерінің болмайтынын дәлелдеу.
Шешімдері бірдей теңсіздіктер мәндес теңсіздіктер деп аталады. Шешімдері болмайтын теңсіздіктер де мәндес теңсіздіктер болып есептеледі.
Теңсіздіктерді шешуде теңсіздіктерді мәндес теңсіздіктерге түрлендіру пайдаланылады.
Бір айнымалысы бар сызықтық теңсіздікті ахb теңсіздігіндегі:
а0 болса, теңсіздіктің шешімдері х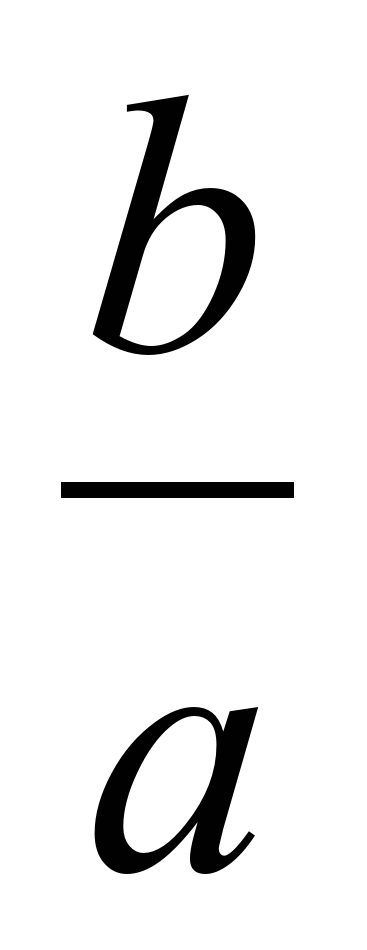 болады.
болады.
Оның сан аралығымен белгіленуі: (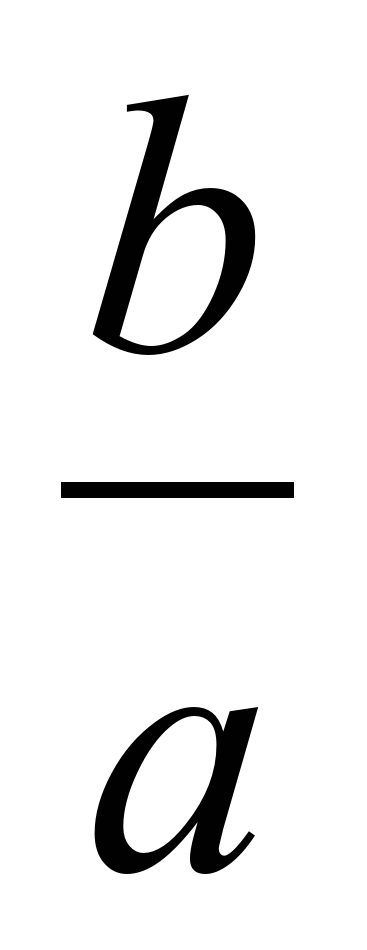 ;+
;+ )
)
1-мысал: 4(х-3)+5х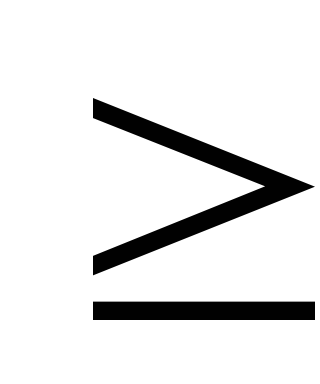 3х
3х
4х-12+5х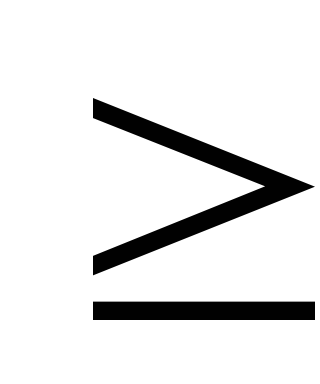 3х
3х
4х+5х-3х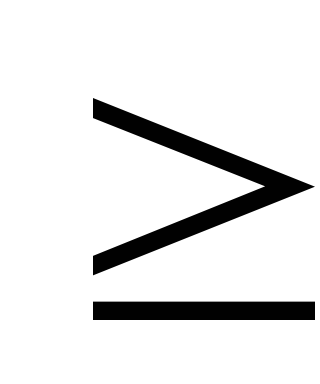 12
12
6х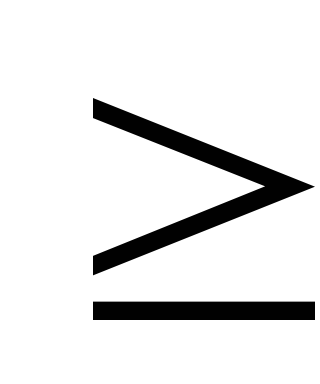 12
12
х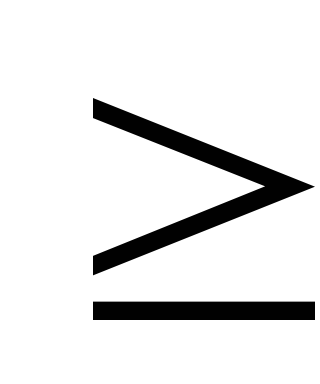 2.
2.
Теңсіздіктің шешімдерінің жиыны 2 саны қоса алынған 2-ден үлкен барлық сандардан құралады.
Теңсіздіктің шешімдер жиыны координаталық түзуде сәуле түрінде кескінделеді.
 //////////////////////////////
//////////////////////////////
 2
2
Жауабын [2; + ) аралығы түрінде немесе х
) аралығы түрінде немесе х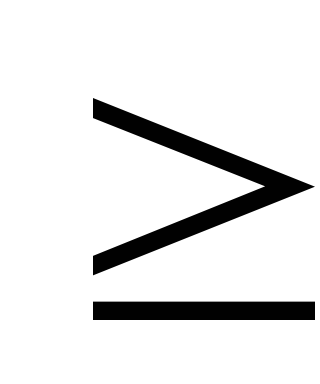 2. теңсіздігі түрінде жазуға болады.
2. теңсіздігі түрінде жазуға болады.
2.аболса, теңсіздіктің шешімдері х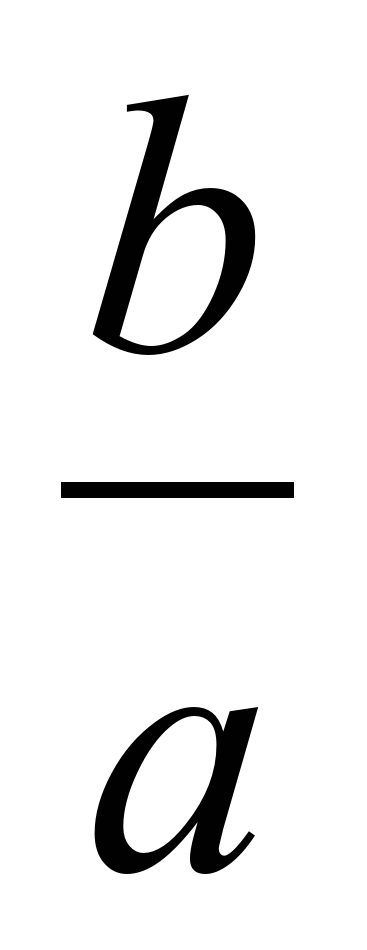 болады.
болады.
Оның сан аралығы мен белгіленуі (- ;
;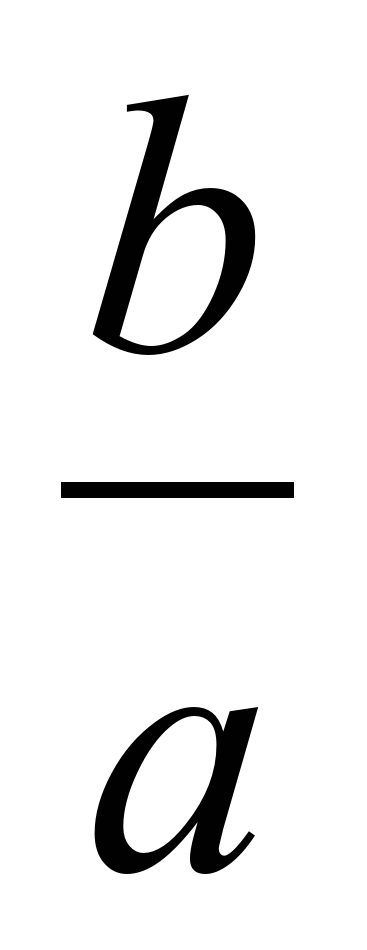 ).
).
а=0 және b0болса,0xb теңсіздігінің шешімдері болмайды. Себебі 0 саны кез келген оң саннан үлкен емес.
3-мысал. 7(х+1)-4х3х+16
7х+7-4х3х+16
3х-3х16-7
0х9
Ж
 ауабы: шешімдері жоқ
ауабы: шешімдері жоқ
а=0 және b0болса,0xb теңсіздігі х-тің кез келген мәнінде тура теңсіздік болады. Себебі нөл саны кез келген теріс саннан (b
үлкен. Сондықтан мұндай теңсіздіктің сансыз көп шешімдері бар.
4-мысал. 6х+17(3х-4)
6х+176х+8
6х-6х8-17
0х-9
Жауабы: сансыз көп шешімдері бар.
3.Толғаныс.
Семантикалық картамен жұмыс
| Атауы
Сан арлықтары |
Интервал |
Кесінді |
Жартылай интервал
|
Сәуле |
Ашық сәуле |
| [-2;4]
(-1;6)
[-4;0]
(0;5)
(- ;4) ;4)
(- ;6) ;6) |
|
|
|
|
|
Белгіленуін пайдаланып жазыңдар.

 ///////////
///////////
- 5 3 х
5 3 х
2

 .
.
-3,7 12 х
3
 . ///////////////
. ///////////////
4 х
4

 . ///////////
. ///////////
-7 3,5 х
Мына теңсіздіктердің шешімдері координаталық түзуде көрсет
х-3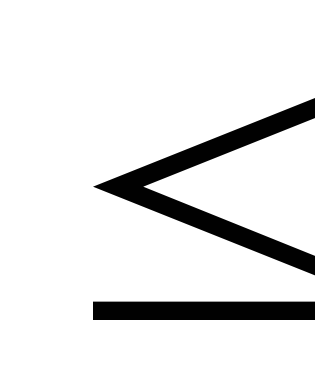 11
11
-3
3x-7
2x+1x+6
Берілген теңсіздіктерді шешіп сан аралықтарын белгілеп, тиісті атауларын
жазып, кестені толтыр.
| № | Теңсіздіктер | Сан аралықтарының белгіленуі | Сан аралықтарының аты |
| 1. | 3х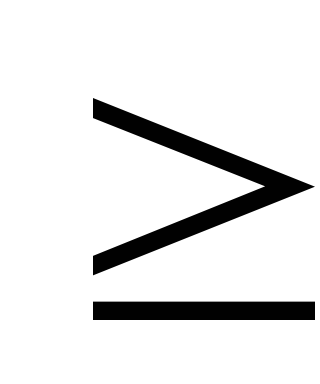 -18 -18 |
|
|
| 2. | -8х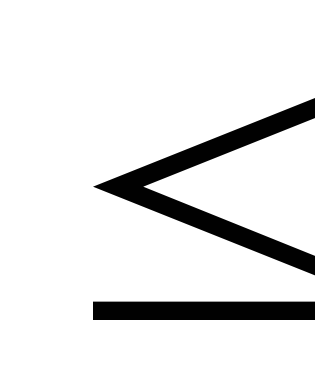 32 32 |
|
|
| 3. | 4х+5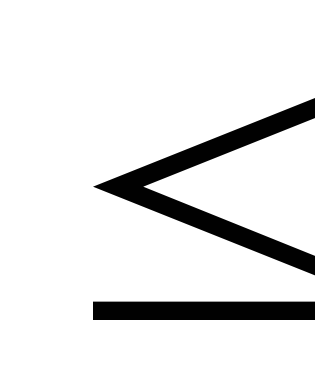 21 21 |
|
|
| 4. | 9х-7-25 |
|
|
Үйге тапсырма: №1011,1012
Бағалау.

 Санды тенсіздік І
Санды тенсіздік І

 а в
а в

 //////////////////////////////
////////////////////////////// 2
2
 ауабы: шешімдері жоқ
ауабы: шешімдері жоқ  .
. 















