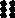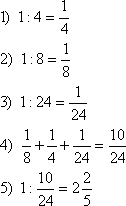Вариант 2
Задача № 1
Незнайка с Гунькой решили сходить в кино и пригласить с собой Кнопочку. Изучи расписание фильмов и планы друзей на эту неделю и определи, на какой фильм они могут пойти все вместе, соблюдая указанные под таблицей условия.
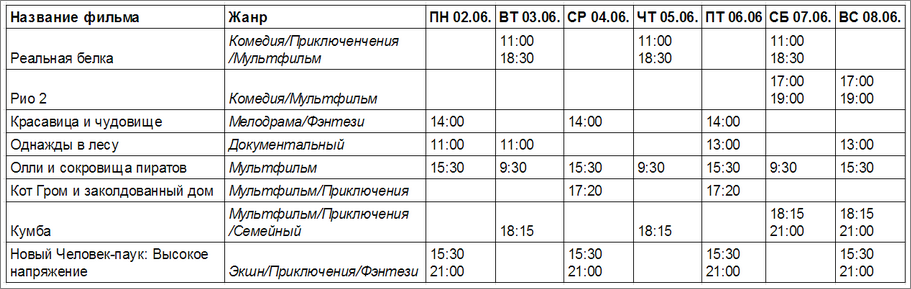

Задача № 2
В овощехранилище привезли 3т картофеля. При сортировке 120 кг составили отходы, а остальной картофель разложили в одинаковые пакеты и отправили в 3 магазина: в первый – 300 пакетов, во второй – 320 пакетов, и в третий – 340 пакетов. Сколько килограммов картофеля было отправлено в каждый магазин?
Задача № 3
На пост мера города претендовало три кандидата: Алексеев, Борисов и Володин. Во время выборов за Володина было отдано в 1,5 раза меньше голосов, чем за Алексеева, а за Борисова – в 4 раза больше, чем за Алексеева и Володина вместе. Сколько процентов избирателей проголосовали за победителя?
Задача № 4
Без подручных средств найдите из представленных ниже примеров тот, итог которого (произведение чисел) отличается от остальных.
А) 2 х 6 х 36
Б) 2 х 15 х 16
В) 12 х 8 х 5
Г) 3 х 32 х 5
Д) 3 х 4 х 40
Задача № 5
Один поезд выехал из города №1 в город №2 со скоростью 40 км/ч. Навстречу ему выехал другой поезд, идущий из города №2 в город №1 со скоростью 60 км/ч. Оба они идут без остановок с постоянной скоростью. На каком расстоянии друг от друга будут эти поезда за 1 час до их встречи?
Задача № 6
Автомобилист посмотрел на счетчик своего автомобиля и увидел симметричное число 15951 км (читается одинаково слева направо или наоборот). Он подумал, что, скорее всего, уже не скоро появится другое симметричное число. Однако уже через 2 часа он обнаружил новое симметричное число. С какой постоянной скоростью автомобилист проехал эти два часа?
Задача № 7
Один господин составил завещание на общую сумму 14000 долларов. Дополнительные условия завещания: если жена родит сына, то сыну достанется вдвое больше, чем матери. Если мать родит дочь, то дочери достанется вдвое меньше, чем матери. В итоге родились близнецы: сын и дочь. Как правильно поделить завещание?
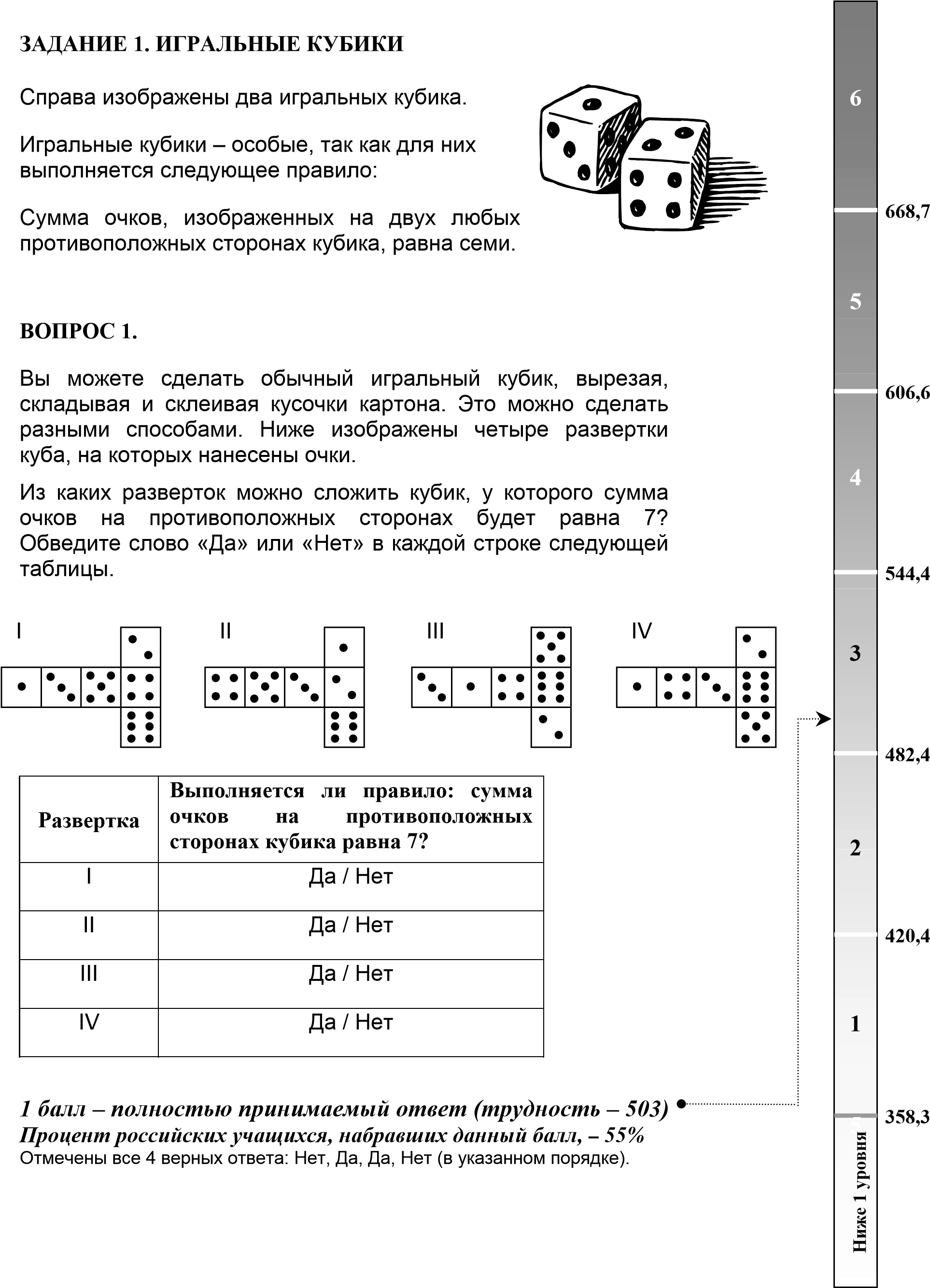
Задача № 8 САДОВНИК
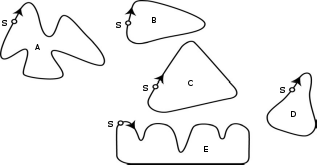
У садовника имеется 32 м провода, которым он хочет обозначить на земле границу клумбы. Форму клумбы ему надо выбрать из следующих вариантов.
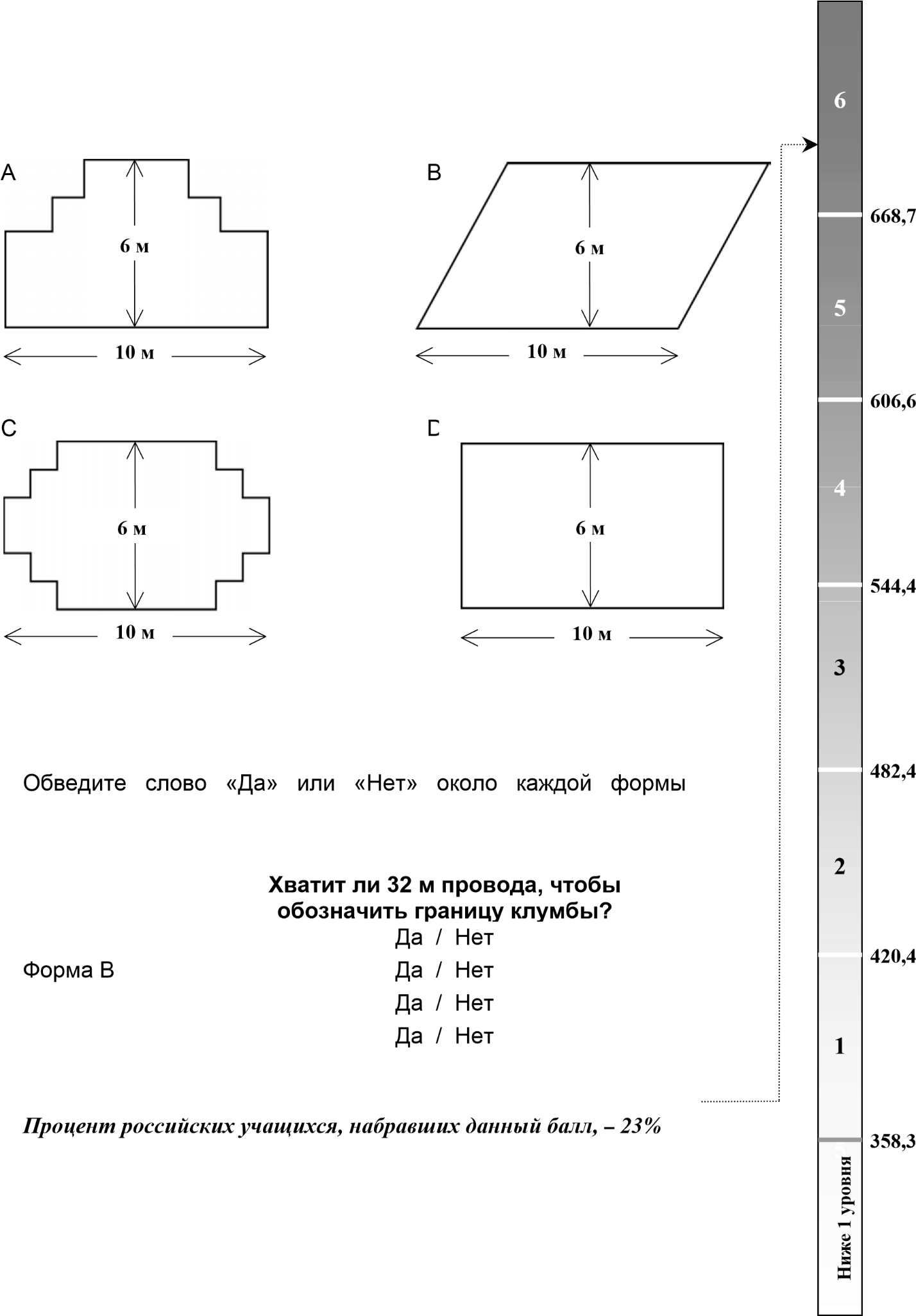
Вопрос. Обведите слово «Да» или «Нет» около каждой формы клумбы в зависимости от того, хватит или не хватит садовнику 32 м провода, чтобы обозначить ее границу.
| Форма клумбы | Хватит ли провода, чтобы обозначить границу клумбы? |
| Форма А | Да/ Нет |
| Форма В | Да/ Нет |
| Форма С | Да/ Нет |
| Форма D | Да/ Нет |
Задача № 9
Задача № 10 Общение в интернете
Марк (из Сиднея в Австралии) и Ганс (из Берлина в Германии) часто общаются друг с другом в Интернете. Им приходится выходить в Интернет в одно и то же время, чтобы они смогли поболтать.
Чтобы определить удобное для общения время, Марк просмотрел таблицы, в которых дано время в различных частях мира, и нашел следующую информацию:
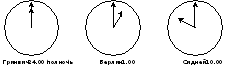
Вопрос 1: ОБЩЕНИЕ В ИНТЕРНЕТЕ
Какое время в Берлине, если в Сиднее 19.00?
Ответ: ....................................................
Вопрос 2: ОБЩЕНИЕ В ИНТЕРНЕТЕ
Марк и Ганс не могут общаться между 9.00 и 16.30 по их местному времени, так как они в это время должны находиться в школе. Они также не могут общаться с 23.00 до 7.00 по их местному времени, так как в это время они будут спать.
Какое время было бы удобно для мальчиков, чтобы они могли поболтать? Укажите в таблице местное время для каждого города.
| Город | Время |
| Сидней | |
| Берлин | |
Задача № 11 Экспорт
На диаграммах представлена информация об экспорте из Зедландии – страны, в которой в качестве денежной единицы используют зед.
Ежегодный экспорт из Зедландии в миллионах зедов, 1996-2000 гг.
Распределение экспорта из Зедландии в 2000 г
![]()
![]()
Вопрос 1:
Какова общая стоимость (в миллионах зедов) экспорта из Зедландии в 1998 г.?
Ответ:.....................................................
Вопрос 2:
Какова стоимость фруктового сока, который экспортировали из Зедландии в 2000 г.?
A 1,8 миллионов зедов B 2,3 миллионов зедов C 2,4 миллионов зедов D 3,4 миллионов зедов E 3,8 миллионов зедов
Задача № 12 Цветные конфеты
Вопрос 1: ЦВЕТНЫЕ КОНФЕТЫ
Мама Роберта разрешила ему вынуть из коробки одну конфету, не заглядывая в коробку.
Число конфет различного цвета в коробке показано на диаграмме.
![]()
Какова вероятность того, что Роберт вынет красную конфету?
Задача №13 Книжные полки
Чтобы собрать один комплект книжных полок, плотнику нужны следующие детали:
4 длинных деревянных панели,
6 коротких деревянных панелей,
12 маленьких скоб,
2 больших скобы и
14 шурупов.
У плотника есть 26 длинных деревянных панелей, 33 коротких панели, 200 маленьких скоб, 20 больших скоб и 510 шурупов.
Вопрос 1: КНИЖНЫЕ ПОЛКИ
Какое наибольшее число комплектов книжных полок может собрать из этих деталей плотник?
Ответ: ....................................................
Задача№ 14 Выбор
В пиццерии всегда можно получить пиццу с двумя обязательными начинками: сыром и помидорами. Но можно заказать пиццу по своему рецепту с дополнительными начинками. Вы можете выбрать из четырех различных дополнительных начинок: оливок, ветчины, грибов и колбасы.
Вера хочет заказать пиццу с двумя дополнительными начинками.
Вопрос:
Сколько у Веры вариантов выбора различных комбинаций из предлагаемых дополнительных начинок?
Ответ: количество вариантов ..............
Задача № 15 Тестовые оценки
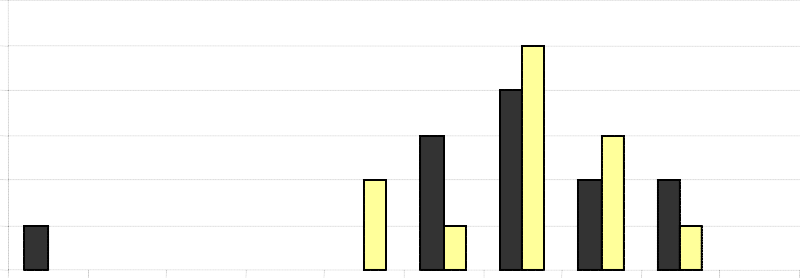
Ниже на столбчатой диаграмме представлены результаты выполнения теста по биологии группами учащихся, обозначенными как Группа А и Группа B.
Средняя оценка группы А равна 62,0 и средняя оценка Группы В равна 64,5.
Считается, что учащийся справился с тестом, если его оценка 50 или более баллов.
Посмотрев на диаграмму, учительница сделала вывод о том, что Группа В выполнила тест лучше, чем Группа А.
Оценки по тесту по биологии
6 Число учащихся
5
4
3
2
1
0 0 - 9
10-19
20-29
30-39
40-49
50-59
60-69
70-79
80-89
90-100
Оценки
![]()
Учащиеся Группы А не согласны с ее мнением. Они стараются убедить учительницу в том, что учащиеся Группы В не обязательно выполнили тест лучше них.
Используя диаграмму, приведите один математический довод, которым могли бы воспользоваться учащиеся Группы А.
Задача № 16 Лестница
На рисунке изображена лестница с 14 ступеньками, высота которой 252 см.
Вопрос:
Какова высота каждой из 14 ступенек?

Длина 400 см
Высота: ................................................. см.
Задача № 17 Последовательность «лесенок»
Роберт рисует последовательность «лесенок», сложенных из квадратов. Ниже показаны этапы построения.


![]()
Этап 1 Этап 2 Этап 3
Видно, что на этапе 1 он использовал один квадрат, на этапе 2 – три квадрата и на этапе 3 – шесть квадратов.
Вопрос 1:
Сколько квадратов он использует на четвертом этапе?
Ответ: количество квадратов...............
Задача № 18 Лучшая машина
Автомобильный журнал использует рейтинговую систему для оценки новых машин и присваивает звание «Машина года» машине, получившей наивысшую общую оценку. Была проведена оценка пяти новых машин, и их рейтинги представлены в таблице.
| Машина | Обеспечение безопасности
(S) | Экономия топлива
(F) | Внешний вид
(E) | Внутренние удобства
(T) |
| Ca | 3 | 1 | 2 | 3 |
| M2 | 2 | 2 | 2 | 2 |
| Sp | 3 | 1 | 3 | 2 |
| N1 | 1 | 3 | 3 | 3 |
| KK | 3 | 2 | 3 | 2 |
Рейтинги означают следующее:
3 очка – Превосходно
2 очка – Хорошо
1 очко – Неплохо
Вопрос:
Для подсчета общей оценки машины журнал использует правило, по которому определяется взвешенная сумма всех очков, полученных машиной:
Общая оценка = 3 · S + F + E + T.
Подсчитайте общую оценку машины «Са». Ответ запишите ниже.
Общая оценка «Ca»: ............................
Задача № 19
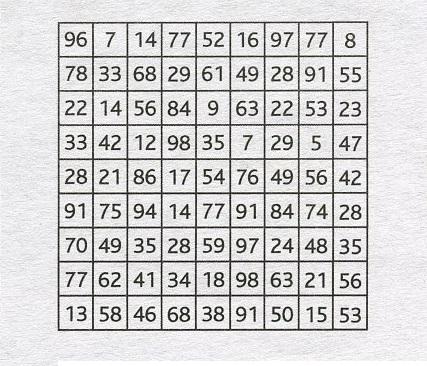
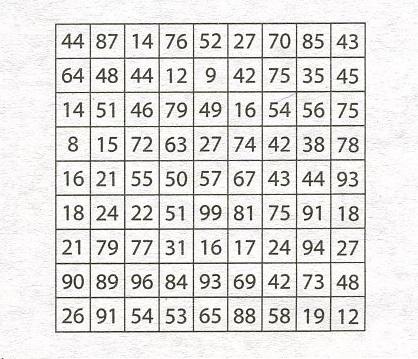
Необходимо найти путь от какого-то квадрата в верхнем ряду сетки до квадрата из нижнего ряда, проходя только через клетки с числами, без остатка делящимися на 3. Нельзя ходить по диагонали.
Задача № 20
При помощи любых арифметических действий составьте число 100 из пяти единиц.
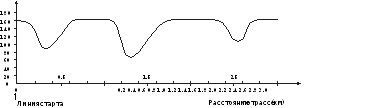
 S - линия старта
S - линия старта