Дисциплина: «Математика»
Для I курса 1, 2 семестр
Контрольно-измерительные материалы(тесты)
Выбрать один правильный ответ:
- Вычислите:
1)20
2)5
3)10
4)8
- Найдите значение выражения: 5 2/7 ·5 5/7
1)5
2)25
3)5 10/49
4)5 ½
- Найдите значение выражения:
2
6 – (0,25)Log 0,25
1) 5, 75
2) 5
3) 4
4) 5,9375
- Найдите область определения функции:
ƒ(х) = Log (х-3)
1)х>9
2)х<3
3)х>3
4)х<9
- Найдите корень уравнения: 23х=8
1)3
2)4
3)1
4)2
- Решите уравнение: Log310 = Log3(х+1) + Log35
1)2
2)1
3)3
4)5
- Найдите корни уравнения: 5х – 25 = 0
1)4
2)3
3)2
4)1
- Решите уравнение: Log53 (х-2) = 0
1)3
2)4
3)5
4)6
- Решите неравенство методом интервалов: х2 – 5х + 6<0
1)(3; 2)
2)(3; 4)
3)(2; 3)
4)(1; 2)
- Найдите значение функции: у=х+?gx в точке х0=10
1)10
2)11
3)12
4)13
- Найдите корень уравнения: 2х=.
1)-2
2)1
3)2
4)3
- Найдите корень уравнения: 512х = 1
1)6
2)3
3)1
4)0
- Упростите выражение: 9 sin2х – 6 + 9 cos2х
1)0
2)3
3)2
4)1
- Найдите значение выражения 8 cos2 - 8 sin2 + 2 sin
1)4
2)3
3)2
4)5
- Переведите из градусной меры в радианную: 180
1)
2)
3)
4)
16. Выразить в градусной мере
1) 100
2) 200
3) 300
4) 400
17. Вычислите arcsin :
1)
2)
3)
4)
18. Найдите корень уравнения 2 sin x =
1) 1
2) 0
3) нет корней
4) (-1)Rarcsin +πR, RЄZ
19. Решите уравнение: 2 cos x – 1 = 0
1)
2)
3)
4)
20. Решите уравнение: 3 sin x · cos x = 0
1) (π; 2 π)
2) (;π)
3) (π+ πR; πR)
4) (πR; + πR)
21. Укажите область значений функции: у = sin x
1) [-1; 1]
2) [0; 1]
3) (-1; 0)
4) (-1; 1)
22. Укажите область определения функции: у = сos x
1) [1; 1]
2) R
3) N
4) (-1; 1)
23. Укажите период функции у = tg x
1) 2 π
2)
3) π
4) 0
24. График какой тригонометрической функции
проходит через точку (0; 1)?
- tg x
- ctg x
- sin x
- cos x
25. Найдите значение выражения: sin22x + (cos2x – sin2x)2
Cos2x + sin2x
- sin x
- cos x
- 1
- 4
26. Решите неравенство методом интервалов: (х-1) (х-2)≤0
1) (1; 2)
2) (-1; 2)
3) (2; 3)
4) (1; 3)
2
27. (2х - 16)х = 0
1) (-1; 0; 1)
2) (0; 1)
3) (0; 2)
4) (-2; 0; 2)
28. Найдите корень уравнения: 2х-1
1) 0
2) 1
3) 2
4) 3
29. График какой тригонометрической функции проходит через точку (0; 0) ?
1) sin x
2) cos x
3) tg x
4) ctg x
30. Укажите область определения функции: у = sin x
1) [-1; 1]
2) (0; 1)
3) (-1; 0)
4) R
Дисциплина: «Математика»
Для I курса 1, 2 семестр
Выбрать один правильный ответ.
ЭТАЛОНЫ ОТВЕТОВ.
1.1
2.1
3.3
4.3
5.3
6.2
7.3
8.1
9.3
10.2
11.1
12.4
13.2
14.3
15.3
16.2
17.4
18.4
19.3
20.4
21.1
22.2
23.3
24.4
25.3
26.1
27.4
28.2
29.1
30.4
Просмотр содержимого документа
«Контрольно-измерительные материалы(тесты) »
Специальность: 060109.51 Сестринское дело, 060108.51 Фармация, 060104.51 Медико-профилактическое дело, 060101.52 Лечебное дело.
Дисциплина: «Математика»
Для I курса 1, 2 семестр
Контрольно-измерительные материалы
Выбрать один правильный ответ:
Вычислите: 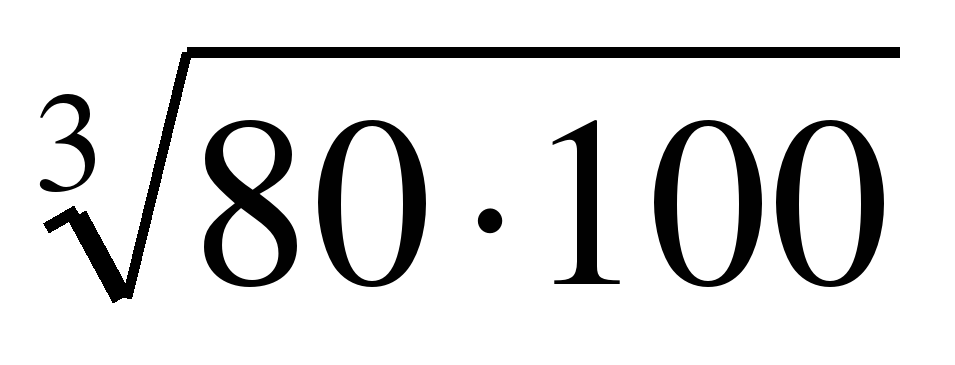
20
5
10
8
Найдите значение выражения: 5 2/7 ·5 5/7
5
25
5 10/49
5 ½
Найдите значение выражения:
2
6 – (0,25)Log 0,25
1) 5, 75
2) 5
3) 4
4) 5,9375
Найдите область определения функции:
ƒ(х) = Log (х-3)
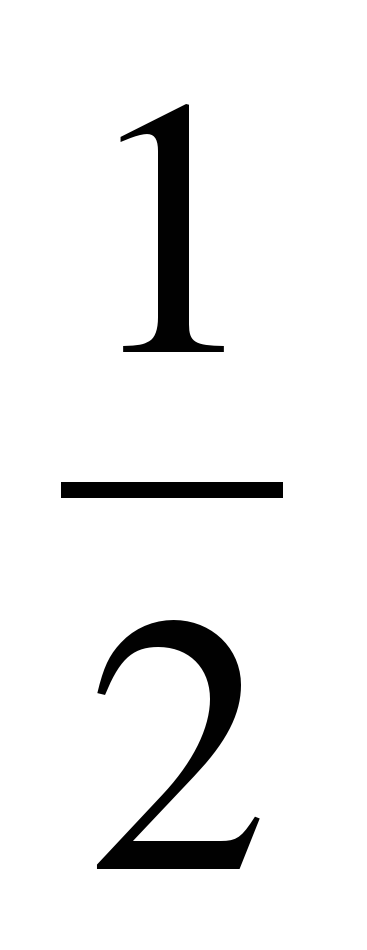
х9
х
х3
х
Найдите корень уравнения: 23х=8
3
4
1
2
Решите уравнение: Log310 = Log3(х+1) + Log35
2
1
3
5
Найдите корни уравнения: 5х – 25 = 0
4
3
2
1
Решите уравнение: Log53 (х-2) = 0
3
4
5
6
Решите неравенство методом интервалов: х2 – 5х + 6
(3; 2)
(3; 4)
(2; 3)
(1; 2)
Найдите значение функции: у=х+ℓgx в точке х0=10
10
11
12
13
Найдите корень уравнения: 2х= .
.
-2
1
2
3
Найдите корень уравнения: 512х = 1
6
3
1
0
Упростите выражение: 9 sin2х – 6 + 9 cos2х
0
3
2
1
Найдите значение выражения 8 cos2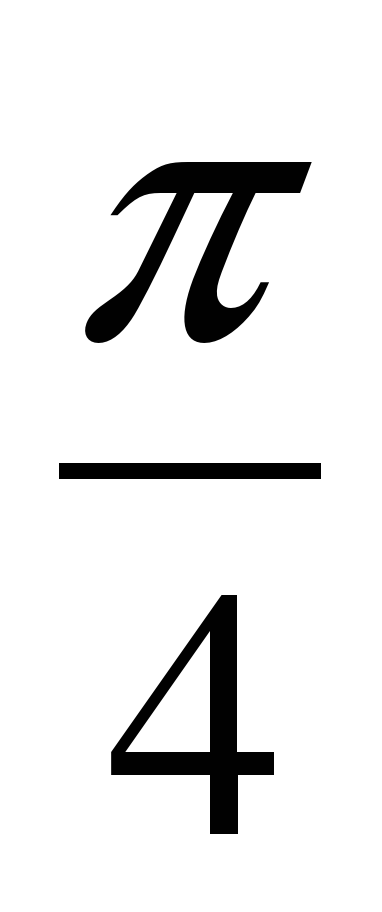 - 8 sin2
- 8 sin2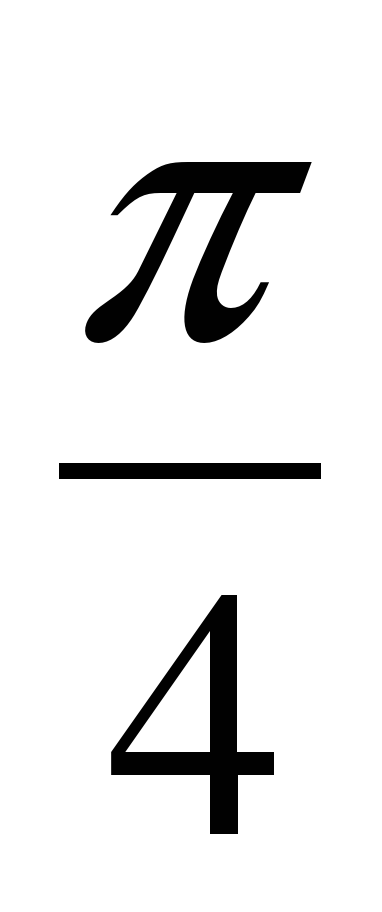 + 2 sin
+ 2 sin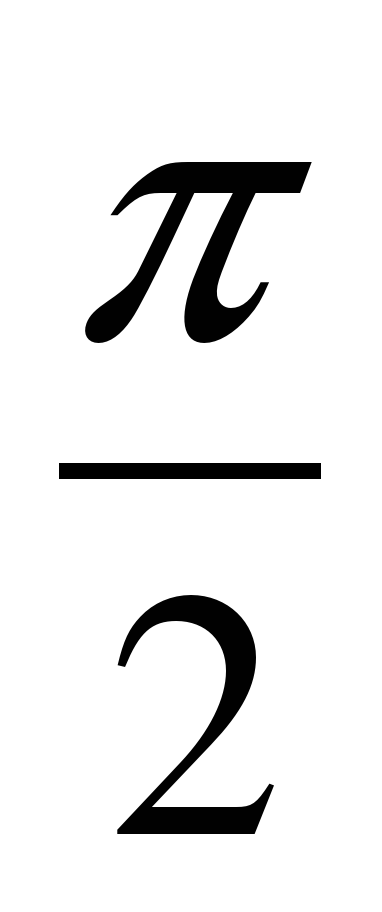
4
3
2
5
Переведите из градусной меры в радианную: 180
1) 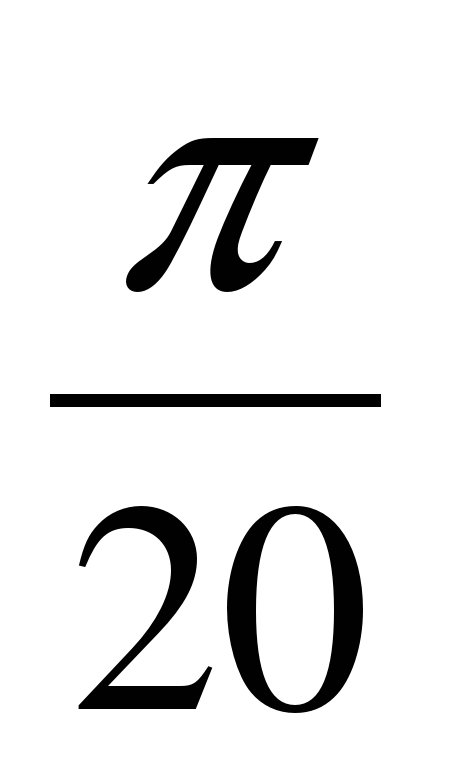
2) 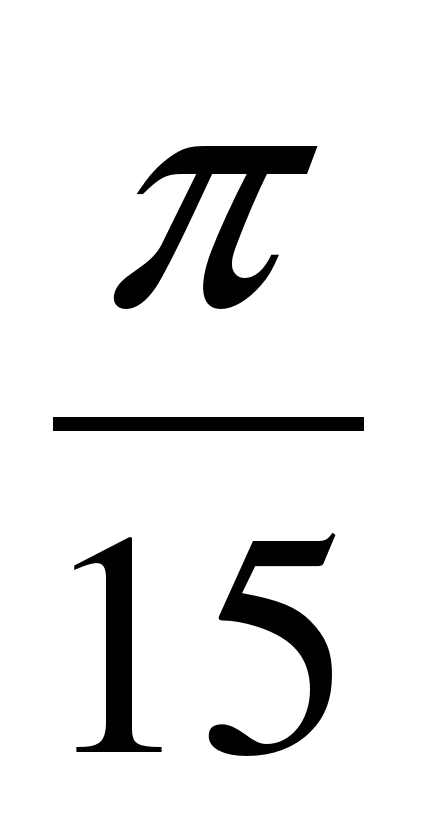
3) 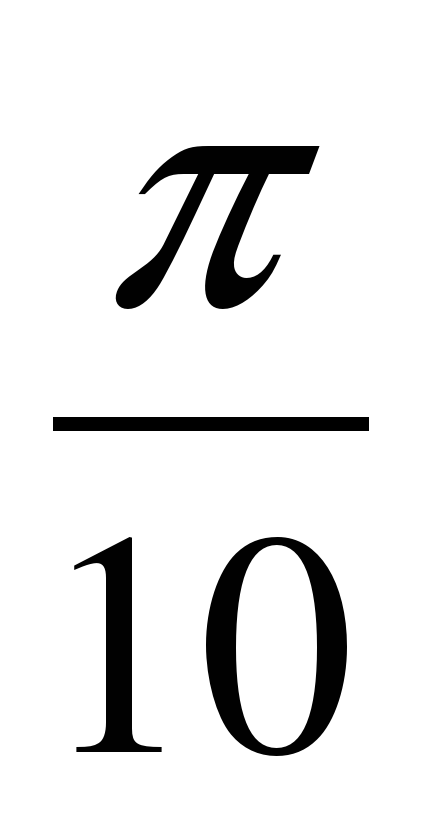
4) 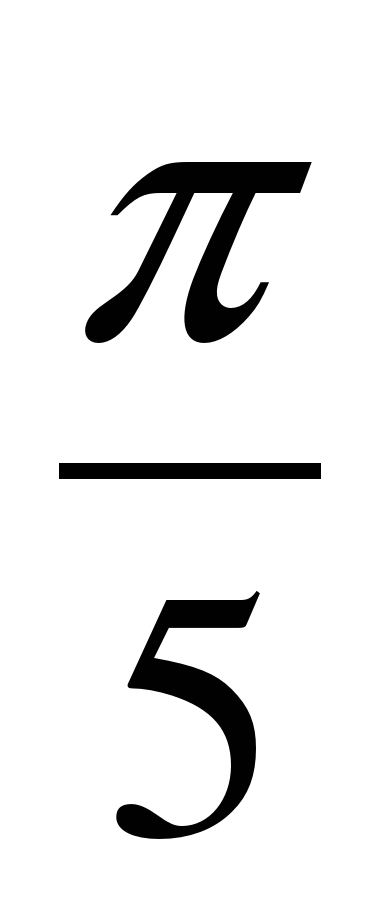
16. Выразить в градусной мере 
1) 100
2) 200
3) 300
4) 400
17. Вычислите arcsin 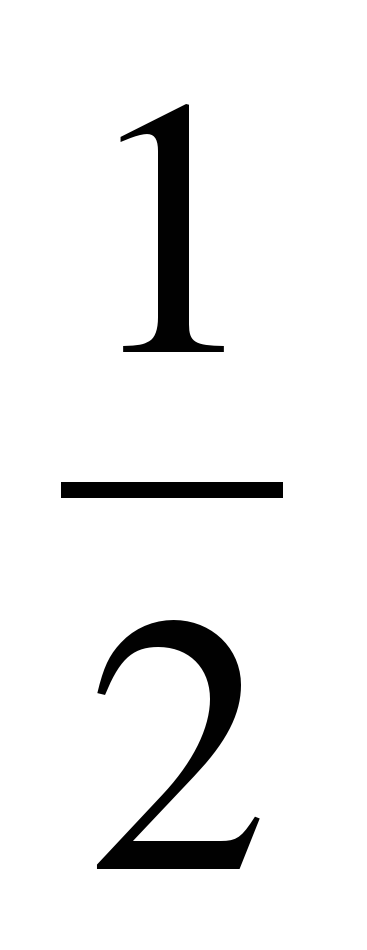 :
:
1) 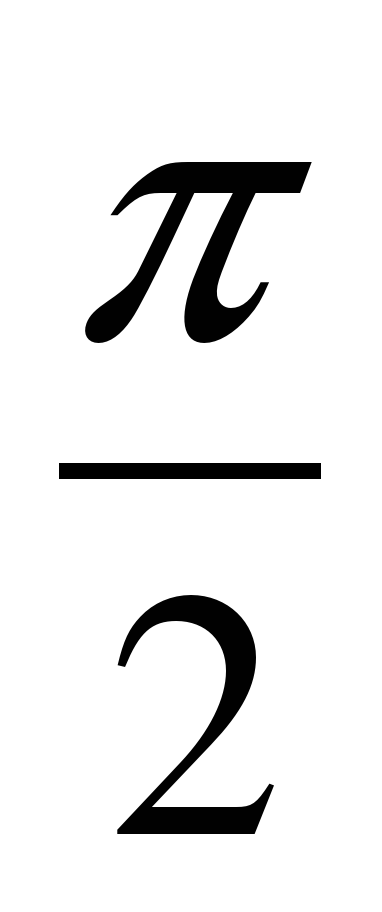
2) 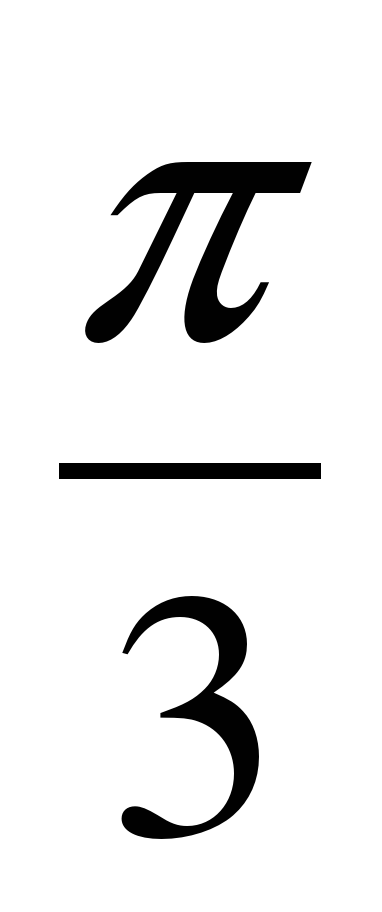
3) 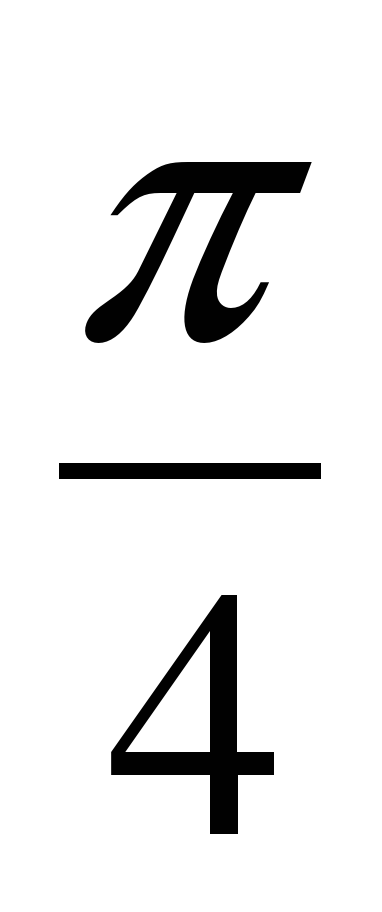
4) 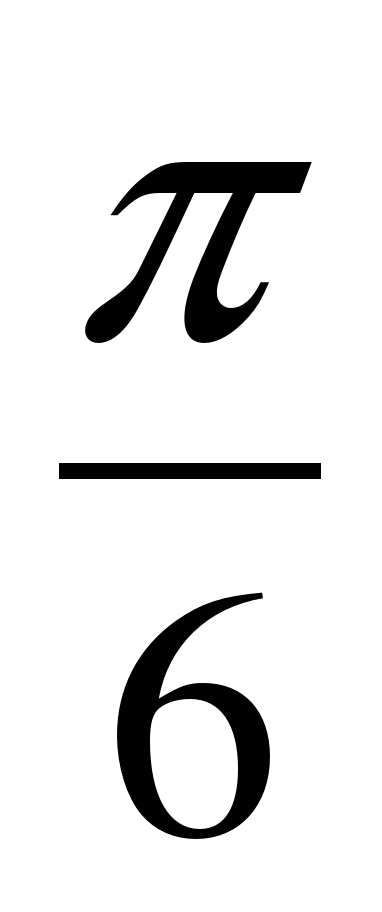
18. Найдите корень уравнения 2 sin x = 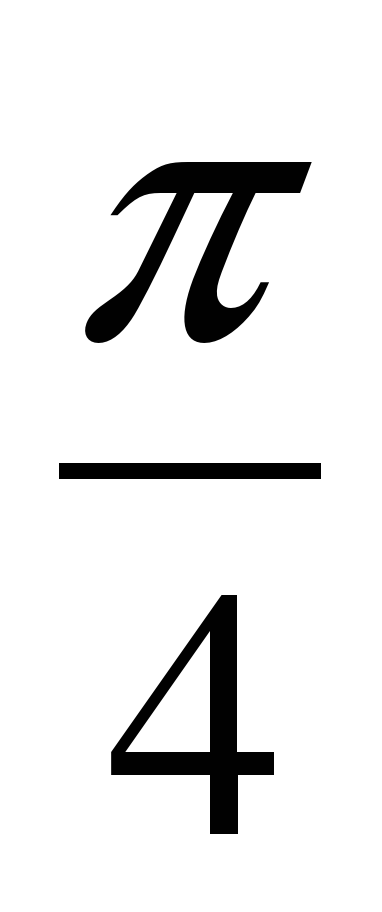
1) 1
2) 0
3) нет корней
4) (-1)Rarcsin 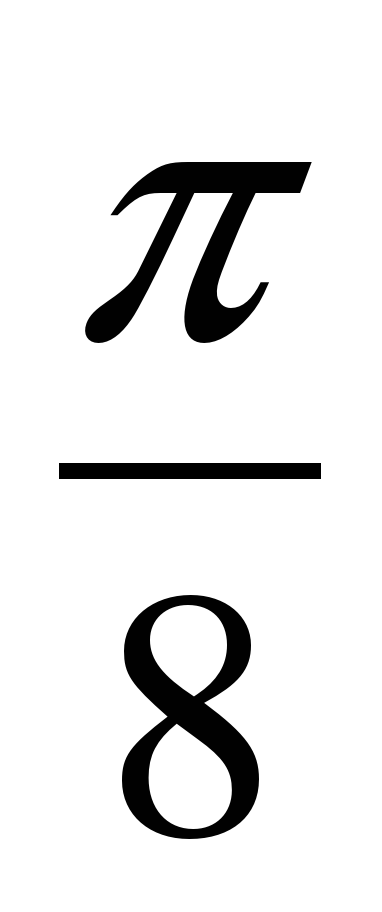 +πR, RЄZ
+πR, RЄZ
19. Решите уравнение: 2 cos x – 1 = 0
1) 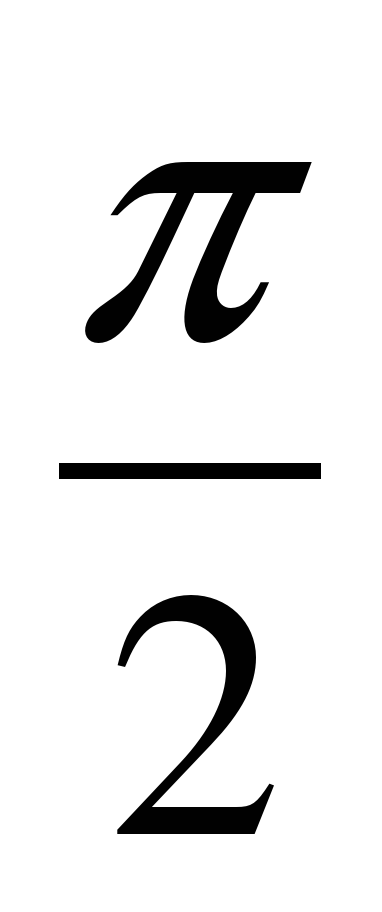
2) 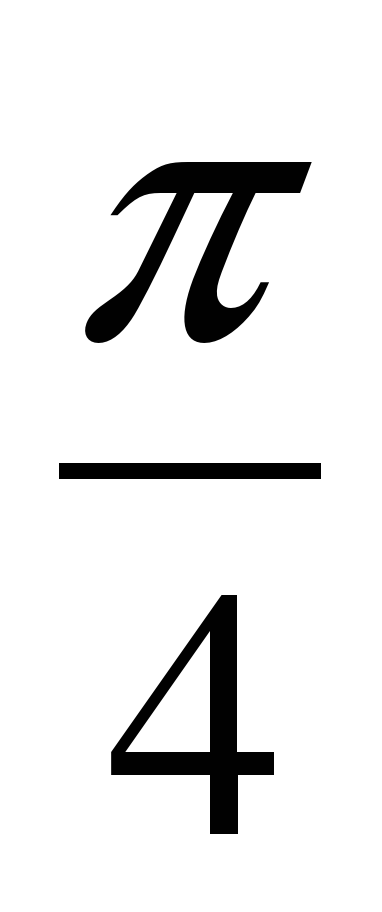
3) 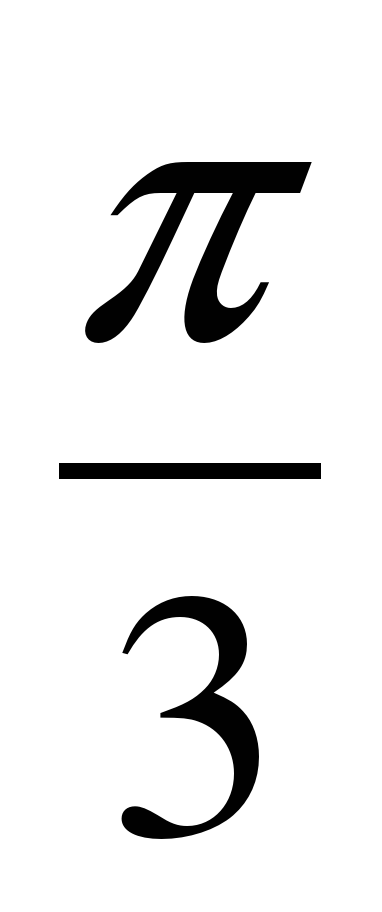
4) 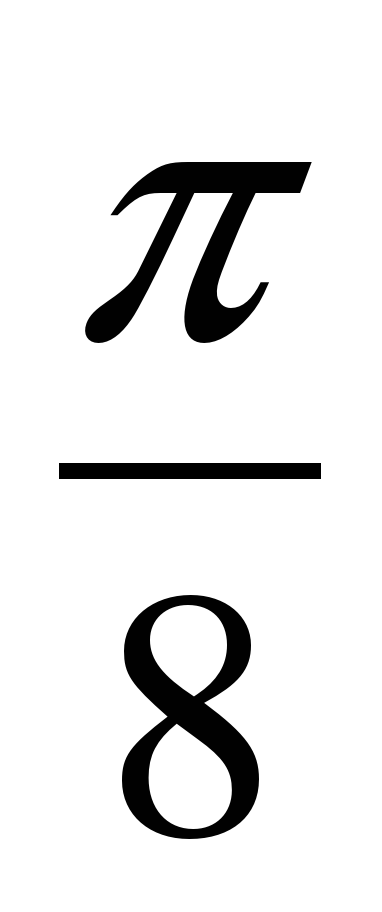
20. Решите уравнение: 3 sin x · cos x = 0
1) (π; 2 π)
2) (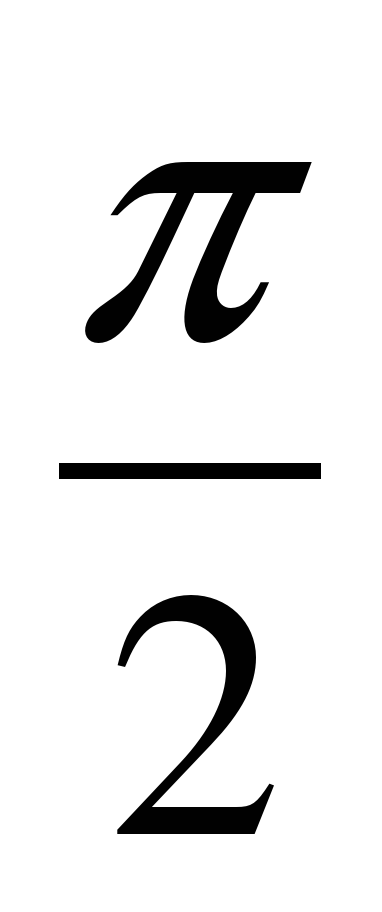 ;π)
;π)
3) (π+ πR; πR)
4) (πR; 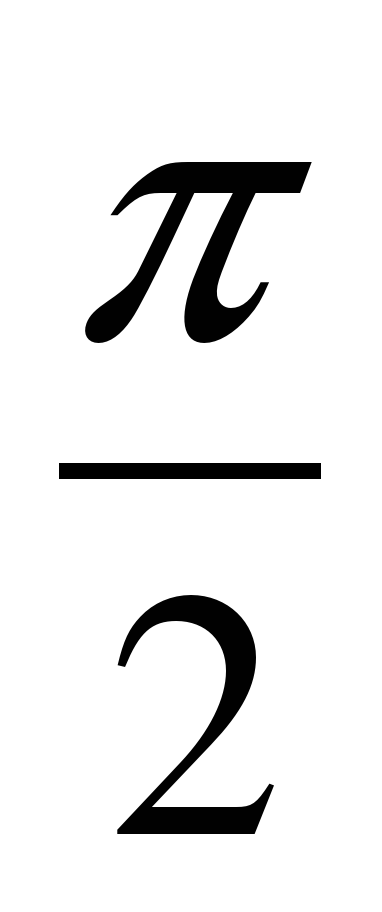 + πR)
+ πR)
21. Укажите область значений функции: у = sin x
1) [-1; 1]
2) [0; 1]
3) (-1; 0)
4) (-1; 1)
22. Укажите область определения функции: у = сos x
1) [1; 1]
2) R
3) N
4) (-1; 1)
23. Укажите период функции у = tg x
1) 2 π
2) 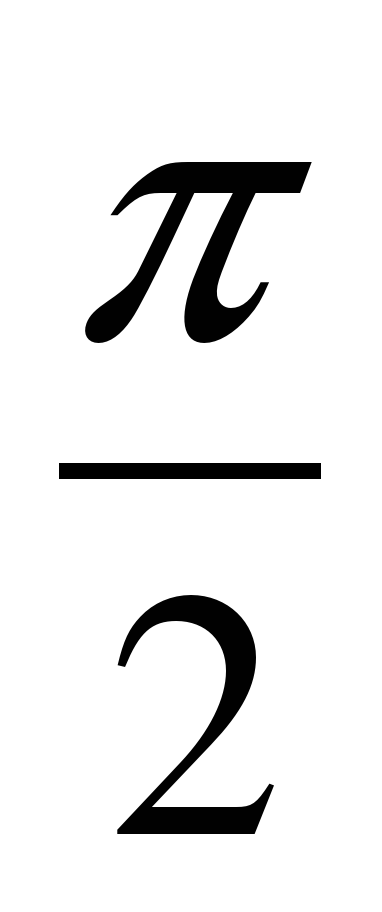
3) π
4) 0
24. График какой тригонометрической функции
проходит через точку (0; 1)?
tg x
ctg x
sin x
cos x
25. Найдите значение выражения: sin22x + (cos2x – sin2x)2
Cos2x + sin2x
sin x
cos x
1
4
26. Решите неравенство методом интервалов: (х-1) (х-2)≤0
1) (1; 2)
2) (-1; 2)
3) (2; 3)
4) (1; 3)
2
27. (2х - 16)х = 0
1) (-1; 0; 1)
2) (0; 1)
3) (0; 2)
4) (-2; 0; 2)
28. Найдите корень уравнения: 2х-1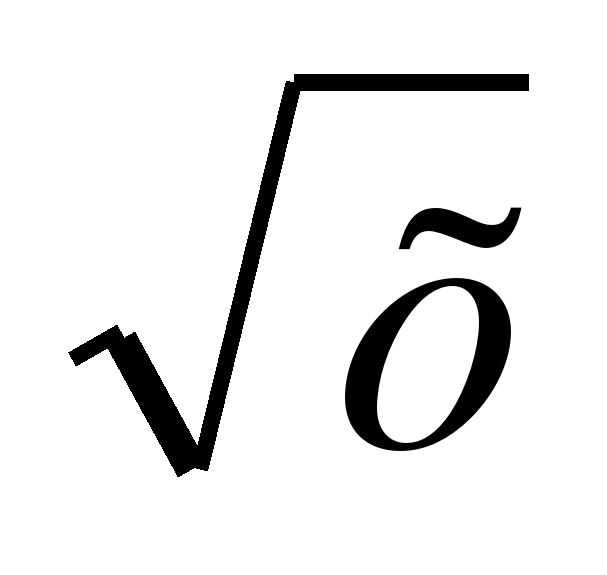
1) 0
2) 1
3) 2
4) 3
29. График какой тригонометрической функции проходит через точку (0; 0) ?
1) sin x
2) cos x
3) tg x
4) ctg x
30. Укажите область определения функции: у = sin x
1) [-1; 1]
2) (0; 1)
3) (-1; 0)
4) R
Дисциплина: «Математика»
Для I курса 1, 2 семестр
Выбрать один правильный ответ.
ЭТАЛОНЫ ОТВЕТОВ.
1
1
3
3
3
2
3
1
3
2
1
4
2
3
3
2
4
4
3
4
1
2
3
4
3
1
4
2
1
4
















