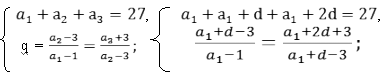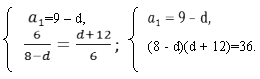МБОУ «Полевской лицей»
Курского района Курской области
Выступление по теме:
Решение и оформление алгебраических задач
второй части государственной итоговой аттестации по математике
Подготовила учитель
математики
Верхне-Гуторовского филиала
МБОУ «Полевской лицей»
Алтухова Лариса
Николаевна
2013-2014 уч.год
Одним из вопросов методики преподавания алгебры является вопрос формирования у учащихся умений и навыков решения текстовых задач. Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.
Широко известны серьезные трудности, которые испытывают учащиеся при решении задач. Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д. Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные. Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся. Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.
Учитывая все выше сказанное, можно считать тему «Методика обучения решению текстовых задач алгебраическим методом» актуальной на сегодняшний день. Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или системы неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным. При решении задач алгебраическим методом основная мыслительная деятельность сосредотачивается на первом этапе решения задачи: на разборе условия задачи и составлении уравнений или неравенств по условию задачи. Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств. Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.
Типичные методические ошибки учителя при работе с текстовыми задачами.
Ошибка 1. Пропуск этапа анализа условия задачи.
«Прочитайте условие задачи. Кто пойдет к доске?» – такое часто можно видеть на уроке. И сразу начинается оформление решения. Этап анализа отсутствует и в некоторых учебниках, и в решебниках. Учителя не всегда сами понимают, зачем нужно проводить этот этап. «Мы уже решали подобные задачи. Зачем проводить этап анализа условия задачи?» На это можно возразить. Может быть, проведение этого этапа обязательно не для всех учащихся. В классе найдутся такие ученики, у которых этап анализа свернут. Они его проходят очень быстро, поэтому сразу видят решение и переходят к его оформлению. Задача педагога – помогать тем, у которых не получается. Решение задачи основывается на тех связях, которые существуют между данными и искомыми величинами. На выделение этих связей и направлен анализ условия задачи. Чтобы помочь учащимся самостоятельно осуществлять анализ условия, преподаватель может предложить им специальные памятки.
Ошибка 2. Пропуск этапа поиска решения.
Пропуск этого этапа ведет к недопониманию учащимися сущности эвристической деятельности, и как результат, к возникновению трудностей при самостоятельном решении задач. В практике обучения традиционной является ситуация, когда учитель вызывает к доске учащегося, который знает, как решить задачу. Однако при личностно ориентированном обучении основная забота учителя должна быть связана с теми, кто испытывает затруднения при самостоятельном решении задач. Тем же учащимся, которые без учителя могут решать задачи, необходимо подбирать задания, усиливающие их умения и способствующие их развитию (составить задачи на основе справочных данных; рассмотреть другие способы решения предложенной задачи; составить граф-схемы других уравнений по задаче и др.)
Ошибка 3. Пропуск этапа исследования решения.
Зачем нужен этот этап? На этапе исследования выясняем, соответствует ли полученный ответ условию задачи (правдоподобность результата); есть ли другие способы решения; что полезного можно извлечь на будущее из решенной задачи. Последний вопрос позволяет рассматривать каждую задачу как звено в общем умении решать задачи, что ведет к накоплению опыта по решению задач.
Ошибка 4. Смешение этапов анализа и поиска решения.
Чтобы этого избежать, надо точно знать, какую цель мы преследуем на каждом этапе. Цель этапа анализа условия – выявить все имеющиеся связи между данными и искомыми величинами, чему помогает составление таблицы (схемы, рисунка). Цель этапа поиска решения – выбрать метод решения (алгебраический или арифметический) и составить план решения. Цели этапов разные, значит, и смешивать эти этапы никак нельзя.
На этапе анализа условия задачи:
разбиваем условие задачи на части;
выясняем, какие величины характеризуют описываемый в условии процесс;
выясняем, какие величины известны, а какие требуется найти;
устанавливаем связи между величинами.
На этапе поиска решения выясняем, что можно найти по данным задачи, и поможет ли это дальнейшему решению. Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:
определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;
составляем схему уравнения, соответствующего выбранному условию;
определяем, какие величины можно обозначить за х; выбираем одну из них;
определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.
Завершается этап поиска составлением плана решения задачи.
Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.
Надо стараться зафиксировать как можно больше таких связей. Почему это важно? Упустив какую-нибудь связь, мы можем потерять:
условие для составления уравнения;
возможность одну величину выразить через другие;
предусмотреть несколько способов решения.
Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.
Обратим внимание на то, что при перечислении этапов, которые мы проходим при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике мы почти везде видим иное: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение. Вот этот момент настолько «закостенел» в нашем сознании, что от него отказаться очень трудно. На самом деле, лучше делать «по-новому». Представьте себя на месте ученика в классе. Рассмотрим ситуацию, когда не были проведены этапы анализа и поиска решения, к доске вызван ученик, который знает, как решить задачу, и он начинает: «За х обозначим…» И что же наш ученик, который затрудняется в самостоятельном решении? Мы из решения сделали тайну непостижимую. «Как он угадал, что обозначить за х?» И когда он будет пробовать дома решать задачу, у него сразу закрадывается сомнение: «А вдруг я не угадаю?» И насколько спокойнее и увереннее чувствует себя наш ученик, если у него есть карточка по проведению анализа и поиска решения задач; он смог составить по условию задачи таблицу; найти несколько условий для составления уравнений; записать схему уравнения для выбранного условия. Ученик знает, что за х можно обозначить любую из неизвестных величин, и, если не получится уравнение по одной схеме, то можно попробовать составить его по другой схеме.
Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.
Очень много зависит от умения ставить (задавать) вопросы учащимся. Вопросы не должны нести в себе подсказку, а подталкивать учащихся к размышлению. Вместо вопросов: «Во сколько туров проходила олимпиада?», «Как распределились посевные площади?», «Какое время находились туристы в пути?», «Какие машины находятся в автопарке?» лучше задавать общие вопросы: «Что происходит по условию задачи?», «Какие объекты участвуют в задаче?», «Какие части можно выделить в задаче?». Вместо вопроса «Можно ли найти такую-то величину?» лучше задать вопрос: «Что можно найти по данным задачи?», поскольку он может вывести на несколько вариантов решения.
Задавая вопросы, учитель не должен вести учащихся к своему решению; нужно рассмотреть все пути решения, выслушать и обсудить все варианты.
Приведу пример решения и оформления некоторых задач.
Рассмотрим задачу 1. Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого.
Решение задачи
Пусть х, км/ч – скорость товарного поезда (х0), у, ч – время движения скорого поезда (у0).
Составляем таблицу.
| Величины Процессы | Расстояние (км) | Скорость (км/ч) | Время (ч) |
| Скорый поезд | (х+50)у | х+50 ? | у |
| Пассажирский поезд | 8/5 х(у+1) | 8/5 х | у+1 |
| Товарный поезд | х(у+4) | х ? | у+4 |
По условию задачи поезда прошли одно и то же расстояние. Получаем систему уравнений
8/5 х(у+1) = х(у+4)
(х+50)у = х(у+4).
По условию задачи х0, тогда
8(у+1) = 5(у+4)
(х+50)у = х(у+4),
3у = 12
(х+50)у = х(у+4),
у = 4
х+50 = 2х,
у = 4
х = 50.
Полученные значения неизвестных удовлетворяют условию х0, у0, значит удовлетворяют условию задачи.
50 км/ч – скорость товарного поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
Ответ: 50 км/ч, 100 км/ч.
Проверка по условию задачи.
50 км/ч – скорость товарного поезда,
4+4 = 8 (ч) – время движения товарного поезда.
50*8 = 400 (км) – расстояние, которое прошёл товарный поезд.
50*8/5 = 80 (км/ч) – скорость пассажирского поезда.
4+1 = 5 (ч) – время движения пассажирского поезда.
80*5 = 400 (км) – расстояние, которое прошёл пассажирский поезд.
4 ч – время движения скорого поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
100*4 = 400 (км) – расстояние, которое прошёл скорый поезд.
Каждый поезд прошёл одно и то же расстояние.
Задача решена верно.
Рассмотрим задачу 2
1. Цена билета на стадион была 150 рублей. После снижения цены билета количество посетителей увеличилось на 50%, а сбор увеличился на 25%. На сколько снизили цену билета?
Решение: Пусть х – первоначальное число посетителей, у – новая цена. После снижения цены, посетителей будет 1,5х, а сбор денег – 1,5ху. Так как первоначально денег собрали 150х, а сбор увеличился на 25%, то получим уравнение: 1,5ху – 150х = 0,25∙150х; у=125.
Ответ: цену снизили на 25 рублей.
Рассмотрим задачу 3
В спортивной секции девочки составляют 60% числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?
Решение: Пусть всего в школе 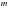 мальчиков и
мальчиков и  девочек. Заметим, что число мальчиков, сидящих с девочками, равно числу девочек, сидящих с мальчиками, т.е. число 0,4
девочек. Заметим, что число мальчиков, сидящих с девочками, равно числу девочек, сидящих с мальчиками, т.е. число 0,4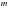 (100% - 60% = 40% от числа
(100% - 60% = 40% от числа 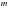 ) равно 0,8
) равно 0,8 (100% - 20% = 80% от
(100% - 20% = 80% от  ). Поэтому
). Поэтому 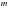 = 2
= 2 , и девочки составляют
, и девочки составляют 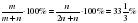 учащихся.
учащихся.
Ответ: 33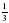 %.
%.
Рассмотрим задачу 4
. Из 40т железной руды выплавляют 20т стали, содержащей 6% примесей. Каков процент примесей в руде?
Решение: 20  100 ∙ 6 = 1,2т – примесей в стали; 20 – 1,2 = 18,8т – чистой стали; 40 – 18,8 = 21,2т – примесей в руде; 21,2
100 ∙ 6 = 1,2т – примесей в стали; 20 – 1,2 = 18,8т – чистой стали; 40 – 18,8 = 21,2т – примесей в руде; 21,2  40 ∙ 100 = 53% - процент примесей в руде. Ответ: 53%.
40 ∙ 100 = 53% - процент примесей в руде. Ответ: 53%.
Рассмотрим задачу 5.
. Арбуз весил 20 кг и содержал 99% воды, когда он немного усох, то стал содержать 98% воды. Сколько теперь весит арбуз?
Решение: Вес «сухого вещества» в арбузе составляет 100 -99 = 1 (%) или 0,01. т. е. 20 · 0,01 = 0,2 (кг). После «усыхания» арбуза вес «сухого вещества» составляет 100 – 98 = 2 (%) или 0,2 : 0,02 = 10 (кг). Ответ: 10 кг.
Рассмотрим задачу 6.
1. Заработок рабочего повысился на 20 %, а цены на продукты и другие товары снизились на 15 %. На сколько процентов рабочий теперь на свой заработок может купить больше товаров, чем прежде?
Решение: Примем прежний заработок рабочего за 10 р. И пусть он покупает только один продукт по 1р. за килограмм, т. е. 10 кг. После повышения на 20 % заработок рабочего стал 12 р, а цена продукта после снижения цены на 15 % - 0,85р. за 1кг. Теперь рабочий может купить 12: 0,85 =14,1 (кг ), т. е. 4,1 : 10 = 0,41, т. е. на 41 5 больше, чем прежде.
Ответ: на 41 % больше.
Рассмотрим задачу 7.
Три числа составляют арифметическую прогрессию. Найдите эти числа, если их сумма равна 27, а при уменьшении первого числа на 1, уменьшении второго на 3 и при увеличении третьего на 3, получили геометрическую прогрессию.
Дано: а1+а2 +а3=27 –сумма трёх членов арифметической прогрессии; а1-1; а2 -3; а3+3– геометрическая прогрессия
Найти: а1; а2; а3.
Решение.
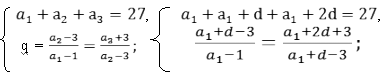
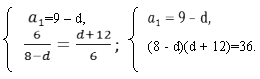
d2 +4d-60=0,
d1=6, d2=-10.
Если d1=6, то 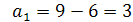 ;
; 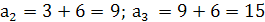 .
.
Если d2=-10, то 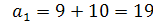 ;
; 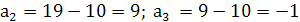 .
.
Ответ: если арифметическая прогрессия 3; 9; 15, то геометрическая прогрессия 2; 6; 18.
Если арифметическая прогрессия 19; 9; -1, то геометрическая прогрессия 18; 6; 2.
Рассмотрим задачу 8.
В каких пропорциях нужно смешать раствор 50 % и 70 % кислоты, чтобы получить раствор 65 % кислоты?
Для решения задачи я предлагаю обучающимся заполнить таблицу, которая находится у них на столе.
| | Концентрация | Масса раствора ( г ) | Масса кислоты ( г ) |
| I раствор | 50 % | х | 0,5х |
| IIраствор | 70 % | у . | 0,7у |
| смесь | 65 % | х + у | 0,65(х + у) |
Заполняем 1-й столбик. Здесь мы указываем концентрацию растворов.
Заполняем 2-й столбик. Здесь мы указываем массу каждого раствора. Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов. Тогда масса смеси будет (х + у) г.
Теперь заполним 3-й столбик. Найдем количество чистой кислоты в 1-ом растворе. Это 0,5х г, во втором растворе 0,7у г, а в смеси будет 0,65(х + у) г кислоты.
По условию задачи составим и решим уравнение.
0,65 (х + у) = 0,5 х + 0,7 у,
65 х – 50 х = 70 у – 65 у,
15 х = 5 у,
3 х = 1 у,
х : у = 1 : 3.
Нужно взять: 1 часть раствора 50% кислоты и 3 части раствора 70% кислоты
Ответ: 50% раствора кислоты -1 часть, 70% раствора кислоты - 3 части.
А также предлагаю обучающимся схему решения этой задачи арифметическим методом, который позволяет решить ее практически устно. Запишем концентрацию каждого раствора кислоты и концентрацию смеси так: 
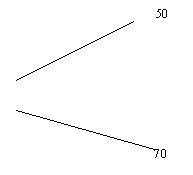
Вычислим, на сколько концентрация первого раствора кислоты меньше, чем концентрация смеси и на сколько концентрация второго раствора кислоты больше, чем концентрация смеси и запишем результат по линиям:
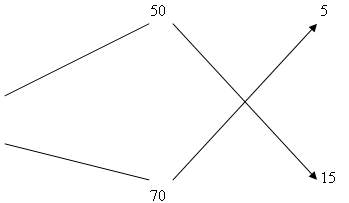
Таким образом, 5 частей нужно взять 50% раствора кислоты и 15 частей 70% раствора кислоты, то есть отношение взятых частей 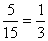 . Окончательно получаем: 50% раствора кислоты-1 часть, 70% раствора кислоты-3 части. Сравните полученные результаты. Делаем вывод: получили один и тот же ответ, но времени затратили гораздо меньше.
. Окончательно получаем: 50% раствора кислоты-1 часть, 70% раствора кислоты-3 части. Сравните полученные результаты. Делаем вывод: получили один и тот же ответ, но времени затратили гораздо меньше.
Вовсе не случайно в старые времена отношение масс смешиваемых вещей находили таким образом.
Проверяя работы ГИА в качестве эксперта, хочется обратить внимание учителей математики на типичные ошибки в оформлении задач обучающимися, за которые снимаются баллы. Обучающиеся:
- «забывают» писать величины в пояснении к составляемому уравнению;
- часто записывают в ответе только найденное число без пояснения;
- делают вычислительные ошибки;
- не делают чертежи к геометрическим задачам.
Использованная литература:
Примерная программа основного общего образования. Математика. / Москва: Просвещение. 2010
Математика. Подготовка к итоговой аттестации. 9 класс / составитель Ф.Ф.Лысенко. Москва. ЛЕГИОН,2013
Подготовка к экзамену по математике ГИА 9 / составитель И.В.Ященко, А.В.Семёнов, П.И.Захаров Москва. МЦНМО. 2014
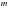 мальчиков и
мальчиков и  девочек. Заметим, что число мальчиков, сидящих с девочками, равно числу девочек, сидящих с мальчиками, т.е. число 0,4
девочек. Заметим, что число мальчиков, сидящих с девочками, равно числу девочек, сидящих с мальчиками, т.е. число 0,4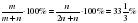 учащихся.
учащихся.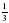 %.
%. 100 ∙ 6 = 1,2т – примесей в стали; 20 – 1,2 = 18,8т – чистой стали; 40 – 18,8 = 21,2т – примесей в руде; 21,2
100 ∙ 6 = 1,2т – примесей в стали; 20 – 1,2 = 18,8т – чистой стали; 40 – 18,8 = 21,2т – примесей в руде; 21,2