Все знают, что извлечь квадратный корень без калькулятора - это очень сложная
задача. Когда нет под рукой калькулятора, то начинаем методом подбора стараться вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. Например, таблица квадратов целых чисел не даёт ответ на такие вопросы, как, например, извлечь корень из 75, 37,885,108,18061 и другие даже приблизительно.
Также часто на экзаменах ОГЭ и ЕГЭ пользование калькулятором запрещено.
Но изучая литературу по данной теме, я узнал, что извлекать корни из таких чисел
люди научились задолго до изобретения микрокалькулятора. Исследуя эту тему, я нашел несколько способов решения данной проблемы.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
«способы извлечения квадратных корней из больших чисел без калькулятора»
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
««способы извлечения квадратных корней из больших чисел без калькулятора»»
Полезное для учителя
Распродажа видеоуроков!
2230 руб.
3190 руб.
2220 руб.
3170 руб.
1970 руб.
2820 руб.
1900 руб.
2710 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



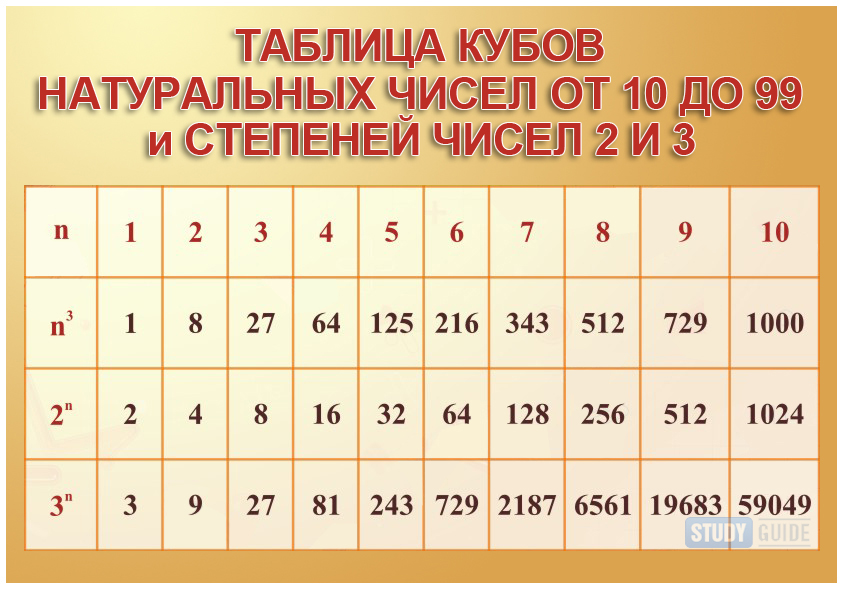
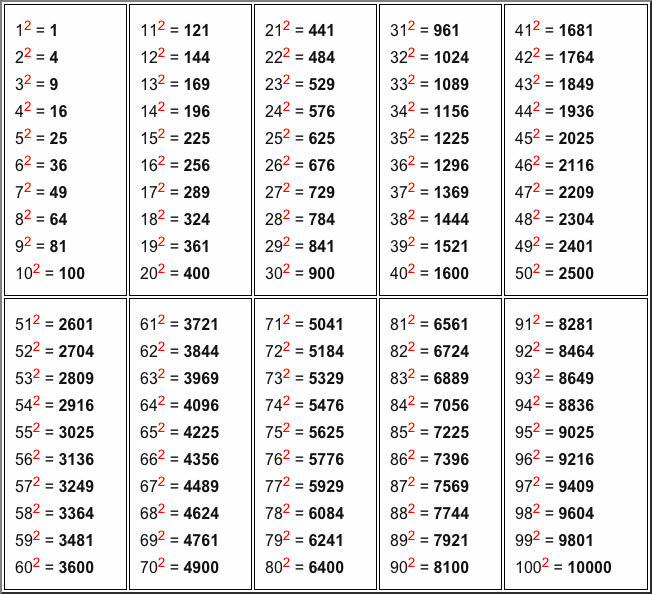 о сразу понятно, что корни, больше 100 уже этим способом извлечь невозможно.
о сразу понятно, что корни, больше 100 уже этим способом извлечь невозможно. остроение графика параболы.
остроение графика параболы.