Реализация требований ФГОС ООО при обучении учащихся 8 класса теме: “Четырёхугольники”

17

ГБОУ ВПО «Академия социального управления»

Дополнительное профессиональное образование

кафедра математических дисциплин

ПРОЕКТ

Реализация требований ФГОС ООО при обучении учащихся 8 класса

теме: “Четырёхугольники”

Выполнил слушатель учебного курса «Актуальные проблемы развития профессиональной компетентности учителя математики (в условиях реализации ФГОС)» учитель математики МБОУ Серковская СОШ д. Серково ЩМР МО

Федорова Ирина Юрьевна

Руководитель курса: кандидат педагогических наук, доцент кафедры математических дисциплин

Фирстова Наталья Игоревна

Москва 2013

Содержание:

Стр.

ВВЕДЕНИЕ ГЛАВА 1. Теоретические основы обучения теме «Четырехугольники» § 1. Концепция духовно-нравственного развития и воспитания личности гражданина России § 2. Логико-дидактический анализ содержания темы «Четырехугольники» § 3. Цели обучения геометрии на разных уровнях конкретизации ГЛАВА 2. Организация обучения теме «Четырехугольники» § 4. Карта изучения темы и её использование § 5. Рабочая программа и тематическое планирование по теме (фрагмент) § 6. Диагностические цели обучения и примеры их реализации ЗАКЛЮЧЕНИЕ Список литературы Приложение

3 5 5 7 14 19 19 23 26 35 36 38

ВВЕДЕНИЕ

Актуальность

Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Изучение темы «Четырехугольники» должно обеспечить:

• осознание значения геометрии в повседневной жизни человека;

• формирование представлений о социальных, культурных и исторических факторах становления науки «геометрии»;

• формирование представлений о геометрии как части общечеловеческой культуры, универсальном языке науки.

В результате изучения темы «Четырехугольники» обучающиеся развивают логическое и математическое мышление, овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты; овладевают умениями решения учебных задач; развивают математическую интуицию.

Результаты изучения темы «Четырехугольники» должны отражать:

1) формирование представлений о математике как о методе познания действительности;

2) развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений;

3) овладение геометрическим языком; развитие умения использовать его для описания предметов окружающего мира; развитие пространственных представлений, изобразительных умений, навыков геометрических построений;

4) формирование систематических знаний о четырехугольниках и их свойствах, развитие умений моделирования реальных ситуаций на языке геометрии, исследования построенной модели с использованием геометрических понятий и теорем, аппарата алгебры, решения геометрических и практических задач;

5) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах;

6) формирование умений формализации и структурирования информации, умения выбирать способ представления данных в соответствии с поставленной задачей — таблицы, схемы.

Цель проекта: Реализация требований ФГОС ООО при изучении темы: «Четырехугольники

Для достижения поставленной цели необходимо решение следующих задач.

Задачи исследования.

1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.

2. Выполнить отбор средств обучения теме «Четырехугольники», в том числе средства ИКТ.

3. Разработать таблицу целей и карту обучения теме «Четырехугольники».

4. Составить учебную рабочую программу, тематическое и почасовое планирование образовательных результатов освоения темы «Четырехугольники».

5. Разработать методические рекомендации обучения теме «Четырехугольники» и применить их в учебном процессе.

Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; беседы с учителями, тестирование учащихся, проведение опытной проверки.

ГЛАВА 1. Теоретические основы обучения теме «Четырехугольники»

§ 1. Концепция духовно-нравственного развития и воспитания личности гражданина России

Ценности личности формируются в семье, сообществах, различных коллективах, в сфере массовой информации, искусства, отдыха и т.д. Но наиболее системно, последовательно и глубоко духовно-нравственное развитие и воспитание личности происходит в сфере общего образования, где развитие и воспитание обеспечено укладом школьной жизни.

Воспитание ориентировано на достижение определенного идеала, т.е. образа человека, имеющего приоритетное значение для общества в сложившихся условиях.

Современный национальный воспитательный идеал - это высоконравственный, творческий, компетентный гражданин России, принимающий судьбу Отечества как свою личную, осознающий ответственность за настоящее и будущее своей страны, укорененный в духовных и культурных традициях многонационального народа Российской Федерации.

Важнейшей целью современного российского образования и одной из приоритетных задач общества и государства является воспитание, социально-педагогическая поддержка становления и развития высоконравственного, ответственного, творческого, инициативного, компетентного гражданина России.

Обеспечение духовно-нравственного развития и воспитания личности гражданина России является ключевой задачей современной государственной политики Российской Федерации. Законопослушность, правопорядок, доверие, развитие экономики и социальной сферы, качество труда и общественных отношений - все это непосредственно зависит от принятия гражданином России общенациональных и общечеловеческих ценностей и следования им в личной и общественной жизни.

Таким образом, духовно-нравственное развитие и воспитание обучающихся является первостепенной задачей современной образовательной системы и представляет собой важный компонент социального заказа для образования.

Содержание духовно-нравственного развития и воспитания личности определяется в соответствии с базовыми национальными ценностями и приобретает определенный характер и направление в зависимости от того, какие ценности общество разделяет, как организована их передача от поколения к поколению.

Духовно-нравственное развитие и воспитание личности в целом является сложным, многоплановым процессом. Оно неотделимо от жизни человека во всей ее полноте и противоречивости, от семьи, общества, культуры, человечества в целом, от страны проживания и культурно-исторической эпохи, формирующей образ жизни народа и сознание человека.

Таким образом, сфера общего образования призвана обеспечивать духовно-нравственное развитие и воспитание личности обучающегося для становления и развития его гражданственности, принятия гражданином России национальных и общечеловеческих ценностей и следования им в личной и общественной жизни.

Программы духовно-нравственного развития и воспитания школьников, разрабатываемые и реализуемые общеобразовательными учреждениями совместно с другими субъектами социализации должны обеспечивать полноценную и последовательную идентификацию обучающегося с семьей, культурно-региональным сообществом, многонациональным народом Российской Федерации, открытым для диалога с мировым сообществом.

Основным содержанием духовно-нравственного развития, воспитания и социализации являются базовые национальные ценности, хранимые в социально-исторических, культурных, семейных традициях многонационального народа России, передаваемые от поколения к поколению и обеспечивающие успешное развитие страны в современных условиях.

Традиционными источниками нравственности являются: Россия, многонациональный народ Российской Федерации, гражданское общество, семья, труд, искусство, наука, религия, природа, человечество.

Базовые национальные ценности лежат в основе целостного пространства духовно-нравственного развития и воспитания школьников, т. е. уклада школьной жизни, определяющего урочную, внеурочную и внешкольную деятельность обучающихся. Для организации такого пространства и его полноценного функционирования требуются согласованные усилия всех социальных субъектов-участников воспитания: семьи, общественных организаций, включая и детско-юношеские движения и организации, учреждений дополнительного образования, культуры и спорта, СМИ, традиционных российских религиозных объединений. Ведущая, содержательно определяющая роль в создании уклада школьной жизни принадлежит субъектам образовательного процесса.

Содержание воспитания группируется вокруг базовых национальных ценностей. В педагогическом плане каждая из них формулируется как вопрос, обращенный человеком к самому себе, как вопрос, поставленный педагогом перед обучающимся. Это воспитательная задача, на решение которой направлена учебно-воспитательная деятельность.

Базовые ценности не локализованы в содержании отдельного учебного предмета, формы или вида образовательной деятельности. Они пронизывают все учебное содержание, весь уклад школьной жизни, всю многоплановую деятельность школьника как человека, личности, гражданина.

Система базовых национальных ценностей создает смысловую основу пространства духовно-нравственного развития личности. В этом пространстве снимаются барьеры между отдельными учебными предметами, между школой и семьей, школой и обществом, школой и жизнью.

Воспитание человека, формирование свойств духовно развитой личности, любви к своей стране, потребности творить и совершенствоваться есть важнейшее условие успешного развития России.

§ 2. Логико-дидактический анализ понятий, теорем темы «Четырехугольники»

Цели

Изучение темы «Четырехугольники направлено на достижение следующих целей:

• овладение системой знаний и умений, необходимых для применения в практической деятельности (например в архитектуре: см. для конструирования готических башен из книги Матхауса Роцирера «О камне»), изучения смежных дисциплин (например в физике: нахождение равнодействующей сил с использование правила «параллелограмма»), продолжения образования (например невозможно изучать тему «Многогранники»);

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, способности к преодолению трудностей;

• формирование представлений об идеях и методах геометрии как универсального языка науки и техники;

• воспитание культуры личности, отношения к геометрии как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Фундаментальное ядро темы «Четырехугольники»

Четырёхугольник: определение (вершины – соседние, противолежащие; стороны – соседние, противолежащие; углы – соседние, противолежащие; диагонали; периметр). Параллелограмм: определение, свойство диагоналей, свойство противолежащих сторон (углов), свойство^* биссектрисы угла и свойство^* биссектрис противолежащих углов, признаки (№1-3). Прямоугольник: определение, свойство диагоналей (№1, 2^*), признаки (№1-4). Ромб: определение, свойства диагоналей (№1-3^*), признаки (№1-3). Квадрат: определения (№1, 2), признаки (№1, 2). Теорема Фалеса. Средняя линия треугольника: определение, свойства (№1, 2). Трапеция: определение, основания, боковые стороны, классификация трапеций (равнобокая трапеция: определение, свойство углов, свойства диагоналей (№1, 2^*), признаки (№1-3); прямоугольная трапеция: определение). Средняя линия трапеции: определение, свойства (№1, 2). Теорема о пропорциональных отрезках.

Учебный материал отмеченный * изучается на III уровне.

Определения понятий

Определение: Четырёхугольником называется фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Определение: Параллелограммом называется четырёхугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых.

Определение: Прямоугольник – это параллелограмм, у которого все углы прямые.

Определение: Ромб – это параллелограмм, у которого все стороны равны.

Определение 1: Квадрат – это прямоугольник, у которого все стороны равны.

Определение 2: Квадрат – это ромб, у которого все углы прямые.

Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Определение: Трапецией называется четырёхугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.

Определение: Трапеция, у которой боковые стороны равны, называется равнобокой. Трапеция, у которой боковая сторона перпендикулярна основаниям, называется прямоугольной.

Определение: Отрезок, соединяющий середины боковых сторон называется средней линией трапеции.

Понятие	Ближайшее родовое понятие	Число видовых отличий
Четырёхугольник	геометрическая фигура
Параллелограмм	четырёхугольник	2
Прямоугольник	параллелограмм	1
Ромб	параллелограмм	1
Квадрат	ромб или прямоугольник	1
Трапеция	четырёхугольник	2
Равнобокая трапеция	трапеция	1
Прямоугольная трапеция	трапеция	1
Средняя линия треугольника	отрезок	2
Средняя линия трапеции	отрезок	2

Теоремы

Признак параллелограмма 1: Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то он является параллелограммом (словесная, условная, метод цепочка треугольников).

Признак параллелограмма 2: Если у четырёхугольника две стороны параллельны и равны, то он является параллелограммом (словесная, условная, метод цепочка треугольников).

Признак параллелограмма 3: Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом (словесная, условная, метод цепочка треугольников).

Свойство диагоналей параллелограмма: Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам (словесная, категоричная, метод от противного).

Свойство противолежащих сторон параллелограмма: Противолежащие стороны параллелограмма равны (словесная, категоричная, метод цепочка треугольников).

Свойство противолежащих углов параллелограмма: Противолежащие углы параллелограмма равны (словесная, категоричная, метод цепочка треугольников).

Свойство биссектрисы угла параллелограмма: Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник (словесная, категоричная, аналитико–синтетический метод).

Свойство биссектрис противолежащих углов параллелограмма: Биссектрисы противолежащих углов параллелограмма параллельны (словесная, категоричная, метод цепочка треугольников).

Признак прямоугольника 1: Если у параллелограмма все углы равны, то он является прямоугольником (словесная, условная, аналитико–синтетический метод).

Признак прямоугольника 2: Если у параллелограмма хотя бы один угол прямой, то он является прямоугольником (словесная, условная, аналитико–синтетический метод).

Признак прямоугольника 3: Если у параллелограмма диагонали равны, то он является прямоугольником (словесная, условная, метод цепочка треугольников).

Признак прямоугольника 4: Если у четырёхугольника три угла прямые, то он является прямоугольником (словесная, условная, аналитико–синтетический метод).

Свойство диагоналей прямоугольника 1: Диагонали прямоугольника равны (словесная, категоричная, метод цепочка треугольников).

Свойство диагоналей прямоугольника 2: Диагонали прямоугольника при пересечении делят его на четыре равнобедренных треугольника (словесная, категоричная, аналитико–синтетический метод).

Признак ромба 1: Если у параллелограмма диагонали равны, то он является ромбом (словесная, условная, метод цепочка треугольников).

Признак ромба 2: Если у параллелограмма диагональ является биссектрисой его углов, то он является ромбом (словесная, условная, аналитико–синтетический метод).

Признак ромба 3: Если у четырёхугольника все стороны равны, то он является ромбом (словесная, условная, метод цепочка треугольников).

Свойства диагоналей ромба 1, 2: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов (словесная, категоричная, аналитико–синтетический метод).

Свойство диагоналей ромба 3: Точка пересечения диагоналей ромба равноудалена от его сторон (словесная, категоричная, метод цепочка треугольников).

Признак квадрата 1: Если у прямоугольника диагонали пересекаются под прямым углом, то он является квадратом (словесная, условная, метод цепочка треугольников).

Признак квадрата 2: Если у ромба один угол прямой, то он является квадратом (словесная, условная, аналитико–синтетический метод).

Теорема Фалеса: Если параллельные прямые, пересекающие стороны угла, отсекает на одной его стороне равные отрезки, они отсекают равные отрезки и на другой его стороне (словесная, условная, метод цепочка треугольников).

Свойство средней линии треугольника: Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине (словесная, категоричная, аналитико–синтетический метод).

Свойство углов равнобокой трапеции: У равнобокой трапеции углы при основании равны (словесная, категоричная, аналитико–синтетический метод).

1 свойство диагоналей равнобокой трапеции: У равнобокой трапеции диагонали равны (словесная, категоричная, метод цепочка треугольников).

2 свойство диагоналей равнобокой трапеции: Если у равнобокой трапеции боковая сторона равна меньшему основанию, то диагонали являются биссектрисами острых углов (словесная, условная, аналитико–синтетический метод).

1 признак равнобокой трапеции: Если у трапеции углы при основании равны, то она является равнобокой (словесная, условная, аналитико–синтетический метод).

2 признак равнобокой трапеции: Если у трапеции диагонали равны, то она является равнобокой (словесная, условная, метод цепочка треугольников).

3 признак равнобокой трапеции: Если у трапеции диагонали являются биссектрисами острых углов, то она является равнобокая (словесная, условная, аналитико–синтетический метод).

Свойство средней линии трапеции: Средняя линия трапеции параллельна основаниям и равна их полусумме (словесная, категоричная, метод цепочка треугольников).

Теорема о пропорциональных отрезках: Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки (словесная, категоричная, аналитико–синтетический метод).

Задачи

Группа	Задачи
Четырёхугольник: определение (п. 50 учебника)	учебник: задачи 1,2 раб.тет.: 1–17
Параллелограмм: определение (п. 51 учебника), признаки (№ 1 – п. 51 учебника; №2 – задача 18; №3)	учебник: задачи 3, 4, 17 раб.тет.: 18–21, 24–27 д/м: ОР–18 задачи 7–12 с/р и к/р: С–1 задание 3 5 задач на карточке
Свойство диагоналей параллелограмма (п. 52 учебника)	учебник: задачи 5–7, 22(2), 23(2) раб.тет.: 28–31, 44 д/м: ОР–18 задачи 5, 6 4 задачи на карточке
Свойство противолежащих сторон параллелограмма (п. 53 учебника)	учебник: задачи 8, 10, 20-21, 22(1), 23(1) раб.тет.: 32–36, 43 д/м: ОР–18 задачи 3, 4 с/р и к/р: С–1 задание 2 4 задач на карточке
Свойство противолежащих углов параллелограмма (п. 53 учебника)	учебник: задачи 9, 11–16 раб.тет.: 37–42 д/м: ОР–18 задачи 1, 2 с/р и к/р: С–1 задание 1 4 задач на карточке
Прямоугольник: определение (п. 54 учебника)	учебник: задачи 27–32 раб.тет.: 47–56 д/м: ОР–19 задачи 1,4(2),6(2),11-12 4 задач на карточке
Признаки (№1 – задача 24; №2 – задача 25; №3 – задача 26; №4) прямоугольника	д/м: ОР–19 задачи 4(1), 5(1) 4 задач на карточке
Свойство диагоналей (№1 - п. 54 учебника, 2*) прямоугольника	д/м:ОР-19 задачи 2,3,4(2),5(2),6-10 с/р и к/р: С–2 задание 2 4 задач на карточке
Ромб: определение (п. 55 учебника), признаки (№1 – задача 33; №2 – задача 34; №3 – задача 36)	учебник: задача 37, 39(1) раб.тет.: 57–59 д/м: ОР–20 задачи 1–3 4 задач на карточке
Свойство диагоналей ромба (п. 55 учебника)	учебник: задача 35, 38, 39(2) раб.тет.: 60–63 д/м: ОР–20 задачи 4–6, 15, 17 с/р и к/р: С–2 задание 1 3 задач на карточке
Квадрат: определение (№1 – п. 56 учебника, №2), признаки (№1– задача 40; №2)	учебник: задача 41–47 раб.тет.: 69–70 д/м: ОР–20 задачи 7–14, 16, 18 с/р и к/р: С–2 задание 3 4 задач на карточке
Теорема Фалеса(п. 57 учебника)	учебник: задача 48, 49 раб.тет.: 77–83 д/м: ОР–21 задачи 1, 2, 9, 10 с/р и к/р: С–3 задание 1 5 задач на карточке
Средняя линия треугольника: определение, свойства (№1, 2) п. 58 учебника	учебник: задача 50–58, 74(1,2) раб.тет.: 84–92 д/м: ОР–21 задачи 3–8, 11–13 с/р и к/р: С–3 задание 2, 3 10 задач на карточке
Трапеция: определение, основания, боковые стороны, типы трапеции (п. 59 учебника)	учебник: задача 60–64, 71, 72 раб.тет.: 93–98 д/м: ОР–22 задачи 1–5, 6(1), 7(1,2), 8, 9, 12–14 с/р и к/р: С–4 задание 1, 3 9 задач на карточке
Средняя линия трапеции: определение, свойства (№1, 2) п. 59 учебника	учебник: задача 59, 65–70 раб.тет.: 99–101 д/м: ОР–22 задачи 6(2,3), 7(3), 11 с/р и к/р: С–4 задание 2 6 задач на карточке
Теорема о пропорциональных отрезках (п. 60 учебника)	раб.тет.: 102–107 5 задач на карточке
Построение четвертого пропорционального отрезка (п. 61 учебника)	раб.тет.: 108–110

Необходимо обратить внимание на задачи учебника №18, 24 – 26, 33, 34, 36, 40, 60, так как это теоретический материал, который вынесен за рамки параграфа. Так же особого внимания требуют задачи № 54, 55, 74, так как рассмотренный материал обогащает знания учащихся и часто используется в задачах ГИА и ЕГЭ. Обратить внимание учащихся на историческую задачу из 6-й книги «Начал» Евклида (п.61 учебника).

С целью развития интереса у учащихся к предмету можно предложить им прочитать рассказ Л.Н.Толстого «Много ли человеку земли нужно». После прочтения дать задание построить чертёж по условию задачи Л.Н.Толстого и записать условие на основе прочитанного; пообещать решить задачу при прохождении темы «Площадь трапеции» и проанализировать полученный результат с точки зрения «геометрической экономии».

В результате реализации данной программы учащиеся должны

знать: что такое параллелограмм, его свойства и признаки; прямоугольник, квадрат, ромб, их свойства и признаки; трапеция, виды трапеции, средняя линия трапеции; теорему Фалеса;

уметь:

• определять вид четырехугольника;

• изображать требуемый четырехугольник, выполнять чертежи по условию задачи, проводить элементарные дополнительные построения в результате поиска решения;

• вычислять значения геометрических величин (длин сторон, градусные меры углов);

• осуществлять доказательства при решении задач;

• использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для описания реальных ситуаций на языке геометрии и расчетов.

Учебные задачи:

• учащиеся должны знать и уметь формулировать определения понятий всех видов изученных четырехугольников, использовать данные знания при решении геометрических и прикладных задач;

• учащиеся должны быть знакомы с систематизационной схемой «Виды четырехугольников» и информационной схемой «Условия метрической определённости» (см. приложение № I, II) и уметь их использовать при решении задач;

• учащиеся должны знать свойства (прямые теоремы) и признаки (обратные теоремы) изучаемых четырехугольников, уметь доказывать их и использовать при решении задач.

Типология задач:

1. на вычисление (арифметический способ, алгебраический способ, комбинированный способ);

2. на доказательство (цепочка треугольников, аналитико – синтетический метод, метод от противного);

3. на построение (элементарные построения, цепочка треугольников, метод геометрического места точек).

Средства обучения:

средства наглядности (чертежи, рисунки, схемы, таблицы); учебные компьютерные программы по теме урока; учебник и учебные пособия, дидактические материалы, методические разработки (рекомендации по предмету), рабочие тетради на печатной основе; отдельные тексты, задания, упражнения и задачи для решения учащимися из других учебных пособий.

Методы обучения:

• методы организации и осуществления учебно-познавательной деятельности (объяснение, лекция, беседа, работа с книгой),

• наглядные методы (наблюдение и демонстрация),

• методы стимулирования и мотивации учения (познавательные игры, ситуация успеха),

• методы контроля и самоконтроля в обучение (фронтальный опрос, письменная проверка, графические методы контроля, программированные методы проверки).

Формы контроля и самоконтроля:

использую:

• устный опрос (индивидуальный или фронтальный) на каждом уроке;

• самостоятельные работы по отдельным темам: «Параллелограмм», «Прямоугольник. Ромб. Квадрат», «Теорема Фалеса. Средняя линия треугольника», «Трапеция. Средняя линия трапеции»;

• разноуровневые тесты по темам: «Многоугольники», «Параллелограмм и его свойства», «Ромб. Прямоугольник. Квадрат», «Трапеция»;

• тест с использование программы «Редактор тестов» (Mental Control);

• письменный зачёт по теории;

• контрольные работы по темам: «Параллелограмм», «Трапеция».

§ 3. Цели обучения математике на разных уровнях конкретизации

Цель 1: приобретение учебной информации и развитие интеллектуальных умений при изучении: а) понятий четырехугольник, параллелограмм, прямоугольник, ромб, квадрат, трапеция, прямоугольная трапеция, равнобокая трапеция, средняя линия треугольника и трапеции; б) теоремы Фалеса и теоремы о пропорциональных отрезках, свойств параллелограмма, прямоугольника, ромба, равнобокой трапеции, средней линии треугольника и трапеции, а так же признаков параллелограмма, прямоугольника, ромба, квадрата, равнобокой трапеции; в) решении типовых задач.

Используются и формируются познавательные УУД и действия постановки и решения проблем.

Познавательные логические действия	Познавательные общеучебные действия	Учебные модели
Для освоения понятий
сравнение, анализ, синтез подведение под понятие	составление схемы определения понятия составление набора объектов для подведения под понятие составление классификационной (систематизационной) схемы	схема определения понятия набор объектов для подведения под понятие классификационные и систематизационные схемы
Для освоения теорем, для решения задач
действия, связанные с осмыслением формулировки теоремы (текста задачи распознавание способа записи формулировки краткая запись формулировки вычленение структуры построение чертежа действия, осуществляемые при поиске доказательства: выведение следствий из условия теоремы (задачи) выведение следствий из требования теоремы (задачи) выведение следствий из требования и условия теоремы (задачи) «челнок»	составление схемы поиска доказательства теоремы(решения задачи) выполнение записи доказательства теоремы (решения задачи) составление поисковой области понятий, связанных отношением составление информационной схемы составление предписания для решения типов задач	схема поиска доказательства (решения) знаковая запись доказательства (решения) поисковая область понятий, связанных отношением информационные схемы предписания для решения классов задач

Цель 2: контроль усвоения теоретических знаний: а) понятий четырехугольник, параллелограмм, прямоугольник, ромб, квадрат, трапеция, прямоугольная трапеция, равнобокая трапеция, средняя линия треугольника и трапеции; б) теоремы Фалеса и теоремы о пропорциональных отрезках, свойств параллелограмма, прямоугольника, ромба, равнобокой трапеции, средней линии треугольника и трапеции, а так же признаков параллелограмма, прямоугольника, ромба, квадрата, равнобокой трапеции; в) навыков решения типовых задач.

Используются и формируются познавательные общеучебные и регулятивные УУД.

Познавательные общеучебные действия

• рефлексия способов и условий действия;

• самоконтроль и самооценка процесса и результатов деятельности.

Регулятивные УУД

• контроль усвоения учебной информации;

• оценивания результатов выполненной деятельности;

• самодиагностика и коррекция собственных учебных действий.

Цель 3: применение знаний и интеллектуальных умений при решении геометрических и учебных задач.

Используются и формируются познавательные, коммуникативные и регулятивные УУД.

Этапы решения	УУД
работа с текстом задачи выполнить анализ текста задачи; выполнить при необходимости чертёж; раскрыть термины понятий, данных в условии; записать данные и требование: «Дана» («Найти», «Доказать»).	выполнение знаково-символических действий; формулирование проблемы; выявление необходимой учебной информации.
поиск решения и составление плана вывести следствие из условия задачи; вывести следствие из требования задачи; вывести следствие из требования и условия (если необходимо); если поиск решения закончен, то составить план решения; если поиск решения не закончен – выбрать способ помощи и уровень помощи.	анализ объектов; синтез; выдвижение и обоснование гипотез; выбор способов решения; составление плана деятельности; принятие решения о помощи.
реализация плана ученик выбирает способ записи решения и оформляет его.	стремление к обоснованию каждого шага умение отличать достоверные результаты от правдоподобных умение действовать в соответствие с планом
«взгляд назад» фиксируется конечный результат проводится его критический анализ проводится поиск путей рационализации решения исследуются особые и частные случаи и т.д.	умение оценить правильность решения задачи умение исследовать различные варианты постановки задачи в зависимости от изменения условий умение обобщить или конкретизировать задачу

Цель 4: развитие коммуникативных умений через: включение обучающихся в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах учебно – познавательной деятельности.

Используются и формируются коммуникативные УУД.

Группа коммуникативных учебных действий включает:

1. планирование учебного сотрудничества с учителем и с сверстниками;

2. инициативное сотрудничество в поиске и сборе информации

3. разрешение конфликтов – выявление проблемы конфликта, поиск способов устранения, принятие решения и его реализация;

4. управление поведением партнёра – контроль, коррекция, оценка действий партнёра;

5. умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владение монологической и диалогической формами речи в соответствии с нормами родного языка.

Цель 5: развитие организационных умений.

Используются и формируются регулятивные и познавательные общеучебные УУД.

Познавательные общеучебные действия

• самостоятельное выделение и формулирование познавательной цели (учебной задачи);

• структурирование и моделирование;

• выбор способов решения;

• рефлексия способов и условий действия;

• самоконтроль и самооценка процесса и результатов деятельности.

Регулятивные УУД

• постановка учебной цели;

• составление и реализация плана деятельности;

• контроль усвоения учебной информации;

• оценивания результатов выполненной деятельности4

• самодиагностика и коррекция собственных учебных действий.

Карта обобщенных целей и учебных задач

Формулировки обобщенных целей	Формулировка учебных задач, с помощью которых достигается обобщенная цель			Опознаваемость целей
	Цель считается достигнутой, если ученик:
	I уровень:	II уровень:	III уровень:
Ц 1: приобретение учебной информации и развитие интеллектуальных знаний и умений при изучении: а) понятий четырехугольник, параллелограмм и его частные случаи, трапеция, средняя линия треугольника и трапеции; б) теоремы Фалеса и теоремы о пропорциональных отрезках, свойств параллелограмма, прямоугольника, ромба, равнобокой трапеции, средней линии треугольника и трапеции, а так же признаков параллелограмма, прямоугольника, ромба, квадрата, равнобокой трапеции; в) решении задач.	а) используя определение понятия в учебнике и данный набор объектов, составляет схему определения; формулирует «своими словами» определение понятия, используя составленную схему. б) по развёрнутому плану формулирует утверждение – гипотезу; сверив полученное утверждением с формулировкой теоремы в учебнике, анализирует формулировку теоремы; записывает доказательство теоремы, используя учебник и готовую схему. в) знакомится с решением основных типов задач по готовому предписанию.	а) используя данный набор объектов(возможно, неполный), составляет схему определения изучаемого понятия; формулирует определение понятия, используя составленную схему; составляет схему взаимосвязи понятия с ранее изученными понятиями. б) формулирует по краткому плану утверждение – гипотезу; сверив полученное утверждением с формулировкой теоремы в учебнике, анализирует формулировку теоремы; записывает доказательство теоремы, используя частично заполненную схему и план указанный в схеме поиска; формулирует и обосновывает обратное утверждение. в) знакомится с решением основных типов задач и с помощью учителя разрабатывает предписания по их решению.	а) используя и исследуя указанные объекты, группирует их, составляет схемы определений понятий, формулирует определения понятий; составляет классификационную схему, родословную понятия. б) формулирует самостоятельно высказывание – гипотезу; выполнив анализ заключения и условия, составляет схему поиска и план доказательства и записывает его; сравнив свою запись доказательства и доказательство в учебнике, формулирует идею доказательства, пытается найти другие способы и методы доказательства. в) знакомится с решением основных типов задач и самостоятельно разрабатывает предписания по их решению	а) наличие схемы определения понятий; набора объектов для подведения под понятие; систематизационной и классификационной схемы. б) наличие формулировки теоремы, схемы поиска доказательства, знаковая модель записи доказательства, пошаговый ход доказательства. в) наличие знаковой модели записи решения задачи, предписания для решения типичных задач; информационной схемы.
Ц 2: контроль усвоения теоретических знаний	а) знает формулировки и схемы определений понятий; строит изображение объекта; использует определение понятий при доказательстве теорем б) знает формулировки свойств и признаков объекта; использует их при доказательстве теорем в) решает задачи арифметическим (в 1-3 действия) и алгебраическим способом с использованием свойств четырехугольников; решает задачи на доказательство в 3-5 шагов с использованием определений, свойств и признаков четырехугольников; делит отрезок на n равных частей.		решает задачи комбинированным способом с использованием свойств четырехугольников; решает задачи на доказательство более 6 шагов с использованием определений, свойств и признаков четырехугольников; выполняет построения четырехугольников с помощью циркуля и линейки.	Опыт переработки и использования учебной информации
Ц 3: применение знаний и умений при решении геометрических задач.	Решает простейшие задачи, составляет задачи по готовому чертежу и требованию, аналогичные задачи, использует образцы решения (доказательства) в учебнике или тетради.	Решает задачи 2 уровня сложности, составляет задачи по готовому чертежу без требования, по условию без требования, использует схемы предписания решения (доказательства).	Решает задачи 3 уровня сложности, составляет задачи по неполному условию и без требования, обратные задачи, составляет самостоятельно и использует схемы предписания	Карточки - информаторы; схемы предписания решения всех типов; образцы записей решения.
Ц 4: развитие коммуникативных умений.	Работая в группе рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; организует взаимоконтроль и взаимопроверку; оказывает помощь работающим на предыдущих уровнях; составляет контрольную работу в соответствии со своим уровнем освоения темы, предлагает её решить и проверяет решение; осуществляет поиск информации для подготовки письменного сообщения и устного выступления в соответствии с изучаемой темой.			Приемы контроля, рецензирования и оценки.
Ц 5: развитие организационных умений	Формулирует цели УД; выбирает задачи и решает их; осуществляет самопроверку с использованием образцов, приемов; составляет контрольную работу для своего уровня усвоения; оценивает свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; делает выводы о дальнейших действиях, планирует коррекцию УПД.			Приемы выбора и рефлексии достижения целей; диагностики и коррекции собственной УПД.

ГЛАВА 2. Организация обучения теме «Четырехугольники»

§ 4. Карта изучения темы и её использование

В ходе работы над проектом в рамках ФГОС ООО я разработала карту изучения темы «Четырёхугольники» в курсе геометрии 8 класса. Эта карта вывешивается на стенде для знакомства учащихся с этапами ознакомления темы, где указаны уровни обучения теме, с которыми ребёнок вправе сам определиться, спланировать свои действия при обучении.

Карта включает в себя 8 блоков: I – логическая структура и цели изучения темы; II – блок актуализации знаний учащихся; III – основные понятия, методы, изучаемые в теме; IV – примеры заданий контрольных работ; V –средства обучения теме; VI –задания для внеурочной самостоятельной работы; VII – темы индивидуальных заданий; VIII – перечень УУД для освоения темы.

Карта составляется учителем перед изучением темы, планируя каждый урок, особенно деятельность учащегося во время формирования знаний и дальнейшего изучения темы.

В первом блоке учитель указывает количество часов с указанием целей (ссылка на таблицу целей темы); показывается разбивка темы по часам с указанием пункта учебника; планируются самостоятельные и контрольные работы. Во втором блоке перечисляются знания и умения необходимые ученику для успешного усвоения темы. В третьем блоке указываются основные понятия, теоремы, встречающиеся при изучении темы «Четырёхугольники». С чем должен учащийся познакомиться, какими навыками овладеть. Доступность данной информации позволяет ребятам самостоятельно нацелить себя на изучение темы, спланировать свою деятельность, контролировать успешность изучения и подготовиться к промежуточному и итоговому контролю.

С самостоятельными и контрольными работами (С-1, С-2, С-3, С-4, К-1, К-2) учащиеся могут ознакомится в пособии А.П.Ершовой. Также в открытом доступе должны быть обучающие работы из пособия Н.Б.Мельниковой. Ребёнок в праве поменять уровень усвоения темы, если считает, что один их них усвоен или не усвоен, переходя на уровень выше или ниже соответственно.

Здесь же приведены темы для индивидуальных заданий, что позволит ученику подготовить сообщение, презентацию, развивая интерес к теме и предмету в общем. Данный вид работы предлагается с целью формирования коммуникативных и организационных умений.

Заканчивается карта перечнем УУД, которыми должен овладеть учащийся и на развитие которых нацелена деятельность учителя.

Технологическая карта изучения темы «Четырёхугольники»

Погорелов А.В.. Геометрия: Учеб. для 7–9 кл. общеобразоват. учреждений. – 10-е изд. – М.:Просвещение, 2013. – 224 с.

I.(1) Логическая структура и цели изучения темы «Параллелограмм и его частные случаи»

§6; п.50

§6; п.51; №18

§6; п.52

§6; п.53

§6; п.53

§6; п.54; №24-26

§6; п.54

Решение задач. С-1

§6; п.55; №33, 34, 36

§6; п.55

§6; п.56; №40

Решение задач. С-2

к/р №1

Ц1, Ц4

Ц1, Ц2, Ц4

Ц1, Ц3, Ц5

Ц1, Ц3, Ц4

Ц1, Ц3, Ц4

Ц1, Ц2, Ц4

Ц1, Ц2, Ц4

Ц2, Ц3, Ц4, Ц5

Ц1, Ц2, Ц4

Ц2, Ц3, Ц4, Ц5

Ц1, Ц2, Ц4

Ц2, Ц3, Ц4, Ц5

Ц2, Ц5

II.(1) Блок актуализации знаний учащихся

Знать: существо понятия доказательства; признаки равенства треугольников; теорему о вертикальных углах; свойства углов при параллельных прямых. Уметь: распознавать внутренние накрест лежащие и соответственные углы при параллельных прямых; выполнять чертежи по условию; решать геометрические задачи, опираясь на изученные свойства фигур и отношения между ними, применяя алгебраический аппарат; проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования.

III.(1) Предметные результаты (Ц 2, 3)

Знать: формулировки и схемы понятий четырёхугольника, параллелограмма и его частных случаев; формулировки свойств и признаков параллелограмма и его частных случаев. Уметь: использовать определения понятий, свойства и признаки параллелограмма и его частных случаев при доказательстве теорем и решении практических задач.

IV.(1) Образцы заданий контрольной работы (Ц 5)

V.(1) Средства обучения

1 уровень

Вариант А1, А2 (К-1)

Схема понятий: параллелограмм и его частные случаи. Схемы предписания. Классификационная, информационная, систематизационная схемы.

2 уровень

Вариант Б1, Б2 (К-1)

3 уровень

Вариант В1, В2 (К-1)

VI.(1) Задания для внеаудиторной самостоятельной работы (Ц 2, 3, 5)

1 – 2 уровень

До черты: ОР-18; ОР-19; ОР-20. (Дидактические материалы: Н.Б. Мельникова и др. «Геометрия 7-9»)

3 уровень

После черты: ОР-18; ОР-19; ОР-20. (Дидактические материалы: Н.Б. Мельникова и др. «Геометрия 7-9»)

I.(2) Логическая структура и цели изучения темы «Трапеция. Средняя линия треугольника и трапеции»

§6; п.57

§6; п.58

§6; п.58 С-3

§6; п.59

§6; п.59

§6; п.59 С-4

§6; п.60

§6; п.61

к/р №2

Коррекция

Ц1, Ц3, Ц5

Ц2, Ц3, Ц4, Ц5

Ц2, Ц3, Ц4, Ц5

Ц1, Ц2, Ц4

Ц1, Ц2, Ц4

Ц2, Ц3, Ц4, Ц5

Ц1, Ц3, Ц5

Ц1, Ц3, Ц5

Ц2, Ц5

Ц2, Ц4, Ц5

II.(2) Блок актуализации знаний учащихся

Знать: существо понятия доказательства; признаки равенства треугольников; теорему о вертикальных углах; свойства углов при параллельных прямых; определение, свойства и признаки параллелограмма. Уметь: распознавать внутренние накрест лежащие углы при параллельных прямых; выполнять чертежи по условию и дополнительные построения после анализа условия и требования; решать геометрические задачи, опираясь на изученные свойства фигур и отношения между ними, применяя алгебраический аппарат; проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования.

III.(2) Предметные результаты (Ц 2, 3)

Знать: формулировки и схемы понятий трапеции и её видов, средней линии треугольника и трапеции; формулировки свойств средней линии треугольника и трапеции; формулировки теоремы Фалеса и теоремы о пропорциональных отрезках. Уметь: использовать определения понятий трапеции и средней линии, свойства средней линии, теоремы Фалеса и теоремы о пропорциональных отрезках при решении практических задач.

IV.(2) Образцы заданий контрольной работы (Ц 5)

V.(2) Средства обучения

1 уровень

Вариант А1, А2 (К-2)

Схема понятий: параллелограмм и его частные случаи. Схемы предписания. Классификационная, информационная, систематизационная схемы.

2 уровень

Вариант Б1, Б2 (К-2)

3 уровень

Вариант В1, В2 (К-2)

VI.(2) Задания для внеаудиторной самостоятельной работы (Ц 2, 3, 5)

1 – 2 уровень

До черты: ОР-21; ОР-22. (Дидактические материалы: Н.Б. Мельникова и др. «Геометрия 7-9»)

3 уровень

После черты: ОР-21; ОР-22. (Дидактические материалы: Н.Б. Мельникова и др. «Геометрия 7-9»)

VII. Темы для индивидуальных заданий (Ц 5)

Математики Древней Греции. Фалес Милетский – математик Древней Греции. Два Фалеса – поэт и математик. Шарнирный механизм Джеймса Уатта. Параллелограмм Чебышева. Четырёхугольники вокруг нас. В мире четырёхугольников. Четырёхугольники в природе, архитектуре, быту, технике. «Мир четырёхугольников – это интересно!»

VIII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы (Ц 1-5)

Познавательные УУД

Регулятивные УУД

Коммуникативные УУД

Личностные УУД

Сравнение; Подведение под понятие; Анализ и синтез; Выведение следствий Установление причинно-следственных связей; Построение логической цепи рассуждения, доказательство.

Целеполагание; Прогнозирование; Планирование; Контроль; Оценка; Коррекция; Волевая саморегуляция.

Планирование учебного сотрудничества с учителем и сверстниками; Инициативное сотрудничество в поиске и сборе информации; Разрешение конфликтов – выявление проблемы конфликта, поиск способов устранения, принятие решения и его реализация; Управление поведением партнёра – контроль, коррекция, оценка действий партнёра; Умение выражать свои мысли; владение монологической и диалогической формами речи.

Смысло – образование; Нравственно - эстетическое оценивание; Самопознание; самоопределение; Рефлексия собственной деятельности.

Рабочая учебная программа по геометрии (фрагмент)

Утверждаю Согласовано Рассмотрено на заседании ШМО

Директор МБОУ Серковская СОШ ЩМР Зам. директора по УВР протокол № 1 от 28.08.2013г.

Мирошникова Н.Г. Пичкалёва Т.А. Руководитель ШМО

Фёдорова И.Ю.

Тематическое и почасовое планирование образовательных результатов освоения геометрии

на 2013/2014 учебный год (фрагмент)

Класс: 8 «А»

Учитель: Фёдорова Ирина Юрьевна

Количество часов: 23 часа (2 часа в неделю)

Плановых контрольных уроков: I ч. – контрольная работа №1; II ч. – контрольная работа №2.

Планирование составлено на основе источников:

1. Программы общеобразовательных учреждений. Геометрия. 7–9 классы. Составитель Бурмистрова Т.А.– М.: Просвещение, 2009;

2. Погорелов А.В.. Геометрия: Учеб. для 7–9 кл. общеобразоват. учреждений. – 10-е изд. – М.:Просвещение, 2009;

3. Березина Л.Ю. и др.. Преподавание курса геометрии по учебнику А.В. Погорелова «Геометрия 7 – 9» – М.: Экзамен, 2008;

4. Жохов В.И. и др.. Геометрия. Поурочные разработки. 7 – 9 классы: Кн. для учителя. – М.: Просвещение, 2010;

5. Мельникова Н.Б. и др.. Геометрия. Дидакт. Материалы для 7–9 кл. общеобразовательных учреждений. – М.: Мнемозина, 1998;

6. Гусев В.А., Медяник А.И.. Геометрия. Дидактические материалы 8 класс. –М.: Просвещение, 2010;

7. Ершова А.П. и др.. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. – 7-е изд. – М.: Илекса, 2008;

8. Дудницин Ю.П.. Геометрия. Рабочая тетрадь для 8 класса общеобразовательных учреждений. – М.: Просвещение, 2011;

9. Дудницин Ю.П., Кронгауз В.Л.. Контрольные работы по геометрии 8 класс. – М.: НПО «Образование», 1998;

10. Пирютко О.Н., Рачковский Н.Н., Гуреев Е.М.. Разноуровневые тесты. Геометрия. 8 класс: Справочное пособие. – Мн.: Книжный дом, 2004;

11. Зив Б.Г., Мейлер В.М., Баханский А.Г.. Задачи по геометрии. Пособие для 7-11 классов. 5-е изд. - М.: Просвещение. 2003;

12. Рабинович Е.М.. Задачи и упражнения на готовых чертежах. Геометрия. – М.: ИЛЕКСА, 2007.

Средства обучения: 1) информационная схема «Условия метрической определённости четырёхугольников», систематизационная схема «Виды четырёхугольников»; 2) предписания для деления отрезка на n равных частей, построения четвертого пропорционального отрезка; 3) карточки с приёмами составления задач, составления систематизационной схемы взаимосвязи понятий, доказательства от противного; 4) подсказки к поиску решения задач; 5) Карта изучения темы.

Тематическое планирование составила: Фёдорова Ирина Юрьевна Дата август 2013 Подпись _____________

Условные обозначения: Ц1 – Ц 5 – цель 1 – 5; ДЗ – домашнее задание; УПД – учебно-познавательная деятельность.

Тематическое планирование

№	Название темы урока	Форма урока	Форма обучения	Достижение метапредметных результатов
	Определение четырёхугольников, п. 50	беседа	индивидуальная	Ц 1, Ц 4
	Параллелограмм. Признаки параллелограмма, п. 51	практикум	групповая	Ц 1, Ц 2, Ц 4
	Параллелограмм. Свойство диагоналей параллелограмма, п. 52	урок смешанного типа	фронтальная	Ц 1, Ц 3, Ц 5
	Параллелограмм. Свойство противолежащих сторон параллелограмма, п. 53	урок смешанного типа	сочетание фронтальной и групповой	Ц 1, Ц 3, Ц 4
	Параллелограмм. Свойство противолежащих углов параллелограмма, п. 53	урок смешанного типа	сочетание фронтальной и групповой	Ц 1, Ц 3, Ц 4
	Прямоугольник. Признаки прямоугольника, п. 54	практикум	групповая	Ц 1, Ц 2, Ц 4
	Прямоугольник. Свойства диагоналей прямоугольника, п. 54	практикум	групповая	Ц 1, Ц 2, Ц 4
	Решение задач	практикум	сочетание фронтальной и групповой	Ц 2, Ц 3, Ц 4, Ц 5
	Ромб. Признаки ромба, п. 55	практикум	групповая	Ц 1, Ц 2, Ц 4
	Ромб. Свойства диагоналей ромба, п. 55	урок смешанного типа	сочетание фронтальной и групповой	Ц 2, Ц 3, Ц 4, Ц 5
	Квадрат. Признаки квадрата, п. 56	практикум	групповая	Ц 1, Ц 2, Ц 4
	Решение задач	практикум	сочетание фронтальной и групповой	Ц 2, Ц 3, Ц 4, Ц 5
	Контрольная работа №1	контрольная работа	индивидуальная	Ц 2, Ц 5
	Теорема Фалеса, п. 57	урок смешанного типа	фронтальная	Ц 1, Ц 3, Ц 5
	Средняя линия треугольника, п. 58	урок смешанного типа	сочетание фронтальной и групповой	Ц 2, Ц 3, Ц 4, Ц 5
	Средняя линия треугольника, п. 58	практикум	сочетание фронтальной и групповой	Ц 2, Ц 3, Ц 4, Ц 5
	Трапеция, п. 59	урок смешанного типа	групповая	Ц 1, Ц 2, Ц 4
	Трапеция, п. 59	практикум	групповая	Ц 1, Ц 2, Ц 4
	Средняя линия трапеции, п. 59	урок смешанного типа	сочетание фронтальной и групповой	Ц 2, Ц 3, Ц 4, Ц 5
	Теорема о пропорциональных отрезках, п. 60	урок смешанного типа	фронтальная	Ц 1, Ц 3, Ц 5
	Построение четвертого пропорционального отрезка, п. 61	урок смешанного типа	фронтальная	Ц 1, Ц 3, Ц 5
	Контрольная работа №1	контрольная работа	индивидуальная	Ц 2, Ц 5
	Урок коррекции и рефлексии	зачёт	сочетание индивидуальной и групповой	Ц 2, Ц 4, Ц 5

Внеурочная самостоятельная деятельность:

1. Темы рефератов, выступлений на конференции, математическом вечере, декаде математики и др. (по итогам изучения курса)

1. Математики Древней Греции

2. Фалес Милетский – математик Древней Греции

3. Два Фалеса – поэт и математик

4. Игра: «Что? Где? Когда?» на тему: «Математика в Древней Греции» http://festival.1september.ru/articles/417059/

5. Игра «Счастливый случай» по теме: «Четырёхугольники» http://ru.convdocs.org/docs/index-255.html

6. Игра "Русское лото" по теме "Четырехугольники". http://festival.1september.ru/articles/607202/

1. Тематика долгосрочных проектов по разделу

1. Шарнирный механизм Джеймса Уатта.

2. Параллелограмм Чебышева.

3. Четырёхугольники вокруг нас

4. В мире четырёхугольников

5. Четырёхугольники в природе, архитектуре, быту, технике.

6. «Мир четырёхугольников – это интересно!»

Технологическая карта урока

Предмет, класс	Геометрия, 8 класс	Авторы УМК	А.В.Погорелов
ФИО учителя, школа	Фёдорова Ирина Юрьевна, МБОУ Серковская СОШ ЩМР
Тема урока	Прямоугольник – решение задач. (§6, п.54 учебника)
Тип урока	Урок применения учебной информации (урок – практикум)
Цель урока:	Применение знаний и умений при решении практических задач, контроль усвоения теоретических знаний.

Структура и ход урока

№	Этап урока	Деятельность учителя	Деятельность ученика	УУД	время
	Организационный момент.	Проверяет домашнее задание. Объявляет тему урока.	Сообщают о готовности к уроку и наличии домашнего задания.	Умение осознанно и произвольно строить речевое высказывание в устной форме	2 мин
	Повторение.	Задаёт вопросы, комментирует и корректирует ответы. Сформулируйте определение прямоугольника. Перечислите свойства прямоугольника. Перечислите свойства параллелограмма. Сформулируйте теорему о сумме углов треугольника; теорему о смежных углах; аксиомы измерения углов. Сформулируйте определение периметра.	Отвечают на вопросы учителя.	Анализ, построение логической цепи рассуждений	3 мин
	Включение изученной учебной информации в систему известных знаний.	Помогает назвать нужные теоретические факты, правильно сформулировать отдельные шаги решения, предлагает ребятам оценить товарища.	Учащиеся решают задачи: Диагонали прямоугольника ABCD пересекаются в точке O. Найдите ABD и DBC, если AOB  BOC на 28º. Диагонали прямоугольника ABCD пересекаются в точке O. Найдите AOB и BOC, если ABD  DBC в 2 раза. (ЕГЭ 2010) Биссектрисы AE и DF, прилежащих к большей стороне прямоугольника AD, делят противолежащую сторону BC на три части в отношении 3:1:3. Найдите длины сторон прямоугольника ABCD, если периметр равен 44 см. (Сколько решений имеет задача?)	Составление и реализация плана, установление причинно - следственных связей, построение логической цепи рассуждений, оценка и коррекция собственной деятельности.	25 мин
	Самостоятельная работа.	Консультирует учащихся при выполнении работы, проверяет правильность выполнения.	Самостоятельно решают №2 из С-2 (Ершова А.П. и др. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса.), выбрав уровень сложности. (см. приложение №13)	Самодиагностика и коррекция собственных учебных действий, контроль усвоения УИ.	12 мин
	Итог урока. Рефлексия. Домашнее задание.	Предлагает оценить свою работу на уроке. Дает и поясняет домашнее задание. ДЗ: №49, 54 (Дудницин Ю.П. Геометрия. Рабочая тетрадь для 8 класса)	Проводят самооценку, рефлексию. Записывают домашнее задание.	Анализ и синтез, рефлексия способов и условий действия, взаимоконтроль и взаимооценка УПД.	3 мин

Саморегуляция учащимися УПД при решении задач

Деятельность учащихся в соответствии с компонентами саморегуляции	Помощь учителя
Постановка учебной цели в процессе решения задач: найти способ решения данной задачи
Выявление объективной информации, необходимой для решения задач	Помогает назвать нужные теоретические факты и этапы решения задачи
Соотнесение выявленных средств выполнения УПД с собственными знаниями и умениями	Предлагает кратко повторить
Деятельность в соответствии с этапами решения задачи
Работа с текстом и поиск решения задачи №1: изображение фигуры в соответствии с условием, запись «Дано», «Найти»; задача решается с помощью уравнения (AOB и BOC – смежные углы) следствия из условия: диагонали прямоугольника равны; точкой пересечения делятся пополам; ABO – равнобедренный, у которого углы при основании равны следствия из требования: сумма ABD и DBC равна 90°, так как прямоугольник – это параллелограмм, у которого все углы прямые.	Предлагает вспомнить свойства смежных углов, теорему о сумме углов треугольника, аксиому измерения углов и использовать данные факты при решении задачи
Составление плана решения задачи используя свойства смежных углов с помощью уравнения найти AOB и BOC; используя теорему о сумме углов треугольника найти углы при основании равнобедренного ABO: ABO и OAB (ABD и CAB); используя аксиому измерения отрезков найти DBC.	Предлагает одному из учащихся записать решение задачи на доске и остальным проверить решение и оценить товарища
Реализация плана решения: выполняется запись решение в тетрадях	Проверяет записи в тетрадях
«Взгляд назад» первичное обобщение решения задачи:	Предлагает в общем виде записать решение
Решение задачи №2	Предлагает решить обратную задачу
Обобщение решения обеих задач	Помогает правильно оформить обобщенную схему решения задач
Работа с текстом и поиск решения задачи №3: изображение фигуры в соответствии с условием, запись «Дано», «Найти»; задача решается с помощью уравнения (х – одна часть) следствия из условия: биссектриса AE угла параллелограмма (прямоугольник – это параллелограмм) отсекает равнобедренный треугольник ABE; боковые стороны равнобедренного треугольника равны; отрезок равен сумме частей, из которых состоит; формула периметра прямоугольника Р=2(a+b) следствия из требования: противолежащие стороны параллелограмма равны	Помогает учащимся с построением чертежа
Составление плана решения задачи если х одна часть, то BE=3х, EF=х, FC=3х; отсюда BC=BE+EF+FC=7х так как АВЕ – равнобедренный, то АВ=ВЕ=3х зная формулу периметра прямоугольника, составляем уравнение решив уравнение находим АВ и ВС	Предлагает одному из учащихся записать решение задачи на доске и остальным проверить решение и оценить товарища
Реализация плана решения: выполняется запись решение в тетрадях	Проверяет записи в тетрадях
«Взгляд назад» первичное обобщение решения задачи:	Предлагает рассмотреть другой случай
Составление плана решения задачи если х одна часть, то BF=3х, EF=х, EC=3х; отсюда BC=BF+EF+EC=7х по аксиоме измерения отрезков ВЕ=BF+EF=4х так как АВЕ – равнобедренный, то АВ=ВЕ=4х зная формулу периметра прямоугольника, составляем уравнение решив уравнение находим АВ и ВС	Предлагает одному из учащихся записать решение задачи на доске и остальным проверить решение и оценить товарища
Реализация плана решения: выполняется запись решение в тетрадях	Проверяет записи в тетрадях

Технологическая карта урока

Предмет, класс	Геометрия, 8 класс	Авторы УМК	А.В.Погорелов
ФИО учителя, школа	Фёдорова Ирина Юрьевна, МБОУ Серковская СОШ ЩМР
Тема урока	Средняя линия треугольника. (§6, п.58 учебника)
Тип урока	Урок освоения новой учебной информации (урок – смешанного типа)
Цель урока:	Познакомиться с новым понятием, изучить свойства этого понятия, попытаться применить изученный материал на практике при решении задач.

Структура и ход урока

№	Этап урока	Деятельность учителя	Деятельность ученика	УУД	время
	Организационный момент.	Проверяет домашнее задание. Объявляет и записывает на доске тему урока.	Сообщают о готовности к уроку и наличии домашнего задания.	Умение осознанно и произвольно строить речевое высказывание в устной форме	2 мин
	Повторение.	Задаёт вопросы, комментирует и корректирует ответы. Сформулируйте определение параллелограмма. Сформулируйте свойства противолежащих сторон параллелограмма. Сформулируйте теорему Фалеса.	Отвечают на вопросы учителя.	Анализ, построение логической цепи рассуждений	2 мин
	Создание проблемной ситуации и формулирование проблемы.	Предлагает прочитать тему урока, познакомиться с опорным конспектом урока (ОКУ) и на основе полученной информации сформулировать возможную цель урока.	Записывают тему урока в тетради, знакомятся с опорным конспектом (см. приложение XIV), формулируют цель урока	Целеполагание, действия постановки и решения проблемы	3 мин
	Изучение нового материала.	Предлагает учащимся изучить схему понятия и на её основе сформулировать определение средней линии треугольника, сравнить свое определение с определением в учебнике и записать его в тетрадь.	Изучают схему определения понятия, формулируют определение средней линии треугольника, сравнивают свое определение с определением учебника и записывают его в тетради.	Анализ учебной информации, выдвижение гипотез	7 мин
	Первичное закрепление.	Предлагает учащимся познакомиться с теоремой 6.7 и прочитать доказательство в учебнике; рассмотреть схему доказательства, предложенную учителем (см. ОКУ); вспомнить нужные теоретические факты, используемые при доказательстве; записать доказательство, используя учебник и ОКУ.	записывают в тетрадь формулировку теоремы 6.7, данные, требование; выполняют чертёж и дополнительные построения; составляют план доказательства, используя учебник и ОКУ; записывают доказательство теоремы, используя прием и план, указанный в учебнике и ОКУ.	Составление и реализация плана, установление причинно – следственных связей, построение логической цепи рассуждений, доказательство.	20 мин
	Включение изученной учебной информации в систему известных знаний.	Наблюдает за работой учащихся. Помогает, при необходимости проверяет ответы. Комментирует ход решения	Решают у доски задачу № 55 учебника, используя учебник и ОКУ: «Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма».	Контроль и оценка процесса и результатов деятельности, построение логической цепи рассуждений, выбор эффективных способов решения.	8 мин
	Итог урока. Рефлексия. Домашнее задание.	Предлагает оценить свою работу на уроке. Задает и комментирует домашнее задание. ДЗ: №50 – 52(учебник)	Проводят самооценку, рефлексию. Записывают домашнее задание.	Анализ и синтез, рефлексия способов и условий действия, взаимоконтроль и взаимооценка УПД.	3 мин

Технологическая карта урока

Предмет, класс	Геометрия, 8 класс	Авторы УМК	А.В.Погорелов
ФИО учителя, школа	Фёдорова Ирина Юрьевна, МБОУ Серковская СОШ ЩМР
Тема урока	Трапеция. Признаки равнобокой трапеции (§6, п.59 учебника)
Тип урока	Урок освоения новой учебной информации (урок – практикум)
Цель урока:	Установление истинности утверждений, обратных свойствам равнобокой трапеции

Структура и ход урока

№	Этап урока	Деятельность учителя	Деятельность ученика	УУД	время
	Организационный момент.	Проверяет домашнее задание. Объявляет тему урока.	Сообщают о готовности к уроку и наличии домашнего задания.	Умение осознанно и произвольно строить речевое высказывание в устной форме	2 мин
	Повторение.	Задаёт вопросы, комментирует и корректирует ответы. Сформулируйте определение трапеция. Какие виды трапеции вы знаете? Сформулируйте определения названных понятий. Перечислите свойства равнобокой трапеции.	Отвечают на вопросы учителя по материалу прошлого урока.	Анализ, построение логической цепи рассуждений	3 мин
	Создание проблемной ситуации и формулирование проблемы.	Предлагает сформулировать утверждения, обратные свойствам равнобокой трапеции и сравнить полученные утверждения с ОКУ (см. приложение XIV). Помогает учащимся сформулировать цель урока.	Под руководством учителя формулируют утверждения, обратные свойствам равнобокой трапеции и цель урока.	Целеполагание, действия постановки и решения проблемы. Анализ учебной информации, выдвижение гипотез.	3 мин

	Изучение нового материала.	Делит учащихся на группы по рядам, распределяет признаки по группам. Предлагает учащимся: раскрыть термины понятий, данных в условии; вывести следствия из условия и заключения теоремы; попытаться осуществить поиск решения и сравнить его с планом доказательства теоремы (см. ОКУ); составить план доказательства.	Работают в группе: выполняют анализ формулировки: «Дано», «Доказать»; раскрывают термины понятий; выводят следствия из условия и требования теоремы; проводят поиск и составляют план доказательства; перечисляют обоснования для каждого шага.	Структурирование, анализ и поиск учебной информации, установление причинно – следственных связей, выдвижение гипотез и их обоснование.	10 мин
	Первичное закрепление.	Предлагает учащимся записать доказательство полученных утверждений по вариантам (ряд – вариант), проверяет правильность выполнения задания.	6 учащихся у доски парами по вариантам записывают доказательство полученных утверждений; остальные работают на карточке ОКУ, контролируют и рецензируют ответы у доски (свой вариант).	Построение речевых высказываний, построение логической цепи рассуждений, доказательство, управление поведением партнёра (контроль, коррекция, оценка действий партнёра)	7 мин

	Включение изученной учебной информации в систему известных знаний.	Наблюдает за работой учащихся. Помогает, при необходимости проверяет ответы. Комментирует ход решения	Решают у доски задачи по готовым чертежам: «Определите вид трапеции»		Контроль и оценка процесса и результатов деятельности, построение логической цепи рассуждений	15 мин
			1. ABCE	2.
			3.	4.
			5.	6.
	Итог урока. Рефлексия. Домашнее задание.	Предлагает оценить свою работу на уроке. Дает и поясняет домашнее задание. ДЗ: №97, 9810, заполнить пропуски в карточке ОКУ и выучить теорию.	Проводят самооценку, рефлексию. Записывают домашнее задание.		Анализ и синтез, рефлексия способов и условий действия, взаимоконтроль и взаимооценка УПД.	5 мин

ЗАКЛЮЧЕНИЕ

Социальный заказ школе представлен в «Концепции духовно-нравственного развития и воспитания личности гражданина России». Эта концепция является методологической основой ФГОС ООО второго поколения. В стандарте сформированы требования к предметным, личностным и метапредметным результатам обучения, которые должны быть достигнуты в процессе обучения каждой учебной дисциплине. К метапредметным результатам относятся, в частности, универсальные учебные действия, для формирования которых разработана специальная программа. УУД – это система действий учащегося, обеспечивающая социальную компетентность, способность к самостоятельному усвоению новых знаний и умений, включая организацию самостоятельной учебной деятельности, способность учащегося к саморазвитию посредством сознательного и активного присвоения нового социального опыта.

Организация процесса формирования УУД при обучении математике требует их систематизации, дифференциации, составления ориентировочной основы отобранных действий, включения их в процесс обучения, в неразрывной связи с усвоением учебной информации.

В данном процессе представлен один из возможных вариантов организации процесса формирования УУД при обучении геометрии. При работе над проектом выявлены теоретические основы обучения теме «Четырёхугольники», выполнен отбор средств обучения. Разработана карта целей, карта изучения темы «Четырёхугольники», включающая в себя разноуровневую работу. Была составлена классификационная, информационная и систематизационная схемы, а также схемы основных понятий темы. Разработаны предписания доказательства основных теорем темы. Я предложила фрагмент тематического планирования и фрагменты трёх уроков, где продемонстрировала реализацию требований ФГОС ООО.

Таким образом, цель поставленная в начале работы над проектом полностью достигнута посредством разработки рекомендаций обучения теме «Четырёхугольники», направленных на реализацию требований ФГОС ООО.

СПИСОК ЛИТЕРАТУРЫ:

1. Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя – М.: Просвещение, 2010. – 159 с.

2. Асмолов А.Г. Системно-деятельностный подход к разработке стандартов нового поколения. // Педагогика. – 2009. – № 4. – с. 18-22.

3. Асмолов А.Г., Бурменская Г.В., Володарская И.А., Карабанова О.А., Салмина Н.Г.. Культурно историческая, системно-деятельностная парадигма проектирования стандартов школьного образования // Вопросы психологии – 2007. – № 4 – с. 16-23

4. Березина Л.Ю. и др.. Преподавание курса геометрии по учебнику Погорелова А.В. «Геометрия 7 – 9» – М.: Экзамен, 2008.

5. Боженкова Л.И.. Методика формирования универсальных учебных действий при обучении геометрии. – М.: Бином. Лаборатория знаний, 2013. 205 с.

6. Волошинов А.В.. Математика и искусство. – М.: Просвещение, 1992. – 335с.

7. Глейзер Г.И.. История математики в школе. – М.: Просвещение, 1964. — 376 с.

8. Гусев В.А., Медяник А.И.. Геометрия. Дидактические материалы 8 класс. –М.: Просвещение, 2010. – 96 с.

9. Данилюк А.Я., Кондаков А.М., Тишков В.А.. Концепция духовно-нравственного развития и воспитания личности гражданина России. – М.: Просвещение, 2009. – 24 с.

10. Дудницин Ю.П.. Геометрия. Рабочая тетрадь для 8 класса общеобразовательных учреждений. – М.: Просвещение, 2011. – 136 с.

11. Дудницин Ю.П., Кронгауз В.Л.. Контрольные работы по геометрии 8 класс. – М.: НПО «Образование», 1998. – 56 с.

12. Ершова А.П. и др.. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. – 7-е изд. – М.: Илекса, 2008. – 208 с.

13. Жохов В.И. и др.. Геометрия. Поурочные разработки. 7 – 9 классы: Кн. для учителя. – М.: Просвещение, 2010

14. Зенкевич И.Г.. Эстетика урока математики: Пособие для учителей. – М.: Просвещение. 1981. – 79 с.

15. Зив Б.Г., Мейлер В.М., Баханский А.Г.. Задачи по геометрии. Пособие для 7-11 классов. 5-е изд. - М.: Просвещение. 2003. – 271 с.

16. Коваленко В.Г.. Дидактические игры на уроках математики: Кн. Для учителя. – М.: Просвещение. 1990. – 96 с.

17. Козлова С.А., Рубин А.Г., Гусев В.А.. Геометрия. 7-9 кл.: учеб. Для общеобразоват. учреждений – М.: Баланс, 2014. 320с.

18. Кочетова Л.Ф., Козлова Л.Г. и др.. Геометрия 7–11 классы Развернутое тематическое планирование по программе А.В.Погорелова. – Волгоград: «Учитель», 2009. –92 с.

19. Мельникова Н.Б. и др.. Геометрия. Дидакт. Материалы для 7–9 кл. общеобразовательных учреждений. – М.: Мнемозина, 1998. – 272 с.

20. Перельман Я.И.. Занимательная геометрия. –М.: Гос.изд. технико-теоретической литературы, 1950. – 296 с.

21. Пирютко О.Н., Рачковский Н.Н., Гуреев Е.М.. Разноуровневые тесты. Геометрия. 8 класс: Справочное пособие. – Мн.: Книжный дом, 2004. – 192 с.

22. Погорелов А.В.. Геометрия: Учеб. для 7–9 кл. общеобразоват. учреждений. – 10-е изд. – М.:Просвещение, 2009. – 224 с.

23. Примерные программы по математике. – М.: Просвещение, 2010. – 67 с.

24. Рабинович Е.М.. Задачи и упражнения на готовых чертежах. Геометрия. – М.: ИЛЕКСА, 2007.

25. Семёнов Е.Е.. За страницами учебника геометрии. Пособие для учащихся 7—9 кл. общеобразоват. учреждений. — 2-е изд. перераб. – М.: Просвещение, 1999. – 286 с.

26. Федеральный государственный образовательный стандарт общего основного образования / М-во образования и науки Рос. Федерации. – М.: Просвещение, 2011. – 48 с.

ПРИЛОЖЕНИЕ

1. Систематизационная схема «Виды четырёхугольников»^5

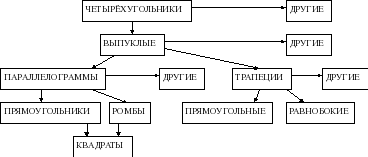
1. Информационная схема «Условия метрической определённости четырёхугольников»^5

Вид четырехугольника	Ближайшее родовое понятие	Число видовых отличий	Число элементов для построения	Некоторые варианты наборов элементов для построения многоугольника
Выпуклый четырёхугольник	Многоугольник		5	Любые пять элементов, из которых хотя бы один линейный
Трапеция	Четырёхугольник	1	4	Любые четыре элемента, из которых хотя бы один линейный
Равнобокая трапеция	Трапеция	1	3	Любые три элементов, из которых хотя бы один линейный
Параллелограмм	Четырёхугольник	2	3	Любые три элементов, из которых хотя бы один линейный
Ромб	Параллелограмм	1	2	Любые два элементов, из которых хотя бы один линейный
Прямоугольник	Параллелограмм	1	2	Любые два элементов, из которых хотя бы один линейный
Квадрат	Квадрат или ромб	1	1	Любой линейный элемент

1. Предписания для деления отрезка АВ на n равных частей

Строим:

1. луч АС;

2. окр.(А;R)АС=С₁; окр.(С₁;R)АС=С₂; …; окр.(С_n-1;R)АС=С_n;

3. А₁С₁А₂С₂…А_n-1C_n-1BC_n;

4. А₁С₁АВ=А₁; А₂С₂АВ=А₂; …; А_n-1C_n-1АВ=А_n-1;

5. А₁; А₂; …; А_n-1 – искомые.

1. Предписания для построения четвертого пропорционального отрезка

Строим:

1. EOF;

2. окр.(O;a)OF=A; окр.(O;b)OF=B; окр.(O;c)OE=C;

3. АСBD;

4. BDOE=D;

5. OD – искомый.

1. Приёмы составления задач^5

   1. составление задачи на вычисление по неполному условию и требованию;

   2. составление задачи на доказательство по данному требованию;

   3. составление задачи на вычисление по данному требованию;

   4. составление задачи на построение по данному требованию;

   5. составление задачи по полному условию без требования;

   6. составление задачи по готовому чертежу и требованию;

   7. составление задачи на доказательство по неполному условию и требованию;

   8. составление обратных задач для данной задачи;

   9. составление задачи посредством конкретизации данной задачи;

   10. составление задачи посредством обобщения данной задачи.

2. Приём доказательства от противного

   1. Делается предположение, противоположное, тому, что требуется доказать.

   2. Выясняется, что получается из сделанного предположения на основании известных теорем и аксиом.

   3. Устанавливается противоречие между тем, что получилось, и тем, что известно из условия, аксиомы или ранее изученных теорем.

   4. Делается вывод: предположение неверно, а верно то, что требуется доказать.

3. Приём составления систематизационной схемы взаимосвязи понятий^5

   1. выделить систематизируемое понятие (определённое через ближайший род и видовые отличия);

   2. выяснить, можно ли разбить объекты, относящиеся к данному понятию, на группы;

а) выявить объем понятия;

б) выяснить, существуют ли объекты, входящие в объем понятия, имеющие видовые отличия;

если да, то к п. 3; если нет, то к п. 5.

1. выбрать основание для разбиения (один из признаков);

2. разбить объекты на группы по выбранному основанию, используя какой-либо способ фиксации связей между объектами;

3. систематизация не выполнена.

1. Структура саморегуляции УПД при освоении математических понятий^5

   Постановка учебной цели в процессе освоения математических понятий, выбор уровня достижения цели
   Репродуктивно - вариативный уровень (I)	Вариативно - эвристический уровень (II)	Эвристический уровень (III)
   Выявление объективной учебной информации, нужной для освоения понятий
   Соотнесение выявленной учебной информации с собственными знаниями и умениями; принятие решения об использовании помощи
   План деятельности при освоении понятий
   1) рассмотреть данный набор объектов; 2) используя определение понятия в учебнике и данный набор объектов, составить схему определения понятия и сверить с эталоном; 3) подвести данные объекты под изучаемое понятие; выделить в наборе те объекты, которые есть в учебнике; 4) сформулировать «своими словами» определение понятия, используя составленную схему	1) используя данный набор объектов (возможно, неполный), разбить их постепенно на две группы, выявляя свойства объектов «главной группы»; 2) составить схему определения изучаемого понятия; 3) сформулировать определение понятия, используя составленную схему, и сравнить с определением в учебнике; 4) составить схему взаимосвязи «открытого» понятия с ранее изученными понятиями	1) используя указанные объекты, исследовать их всевозможные взаимные расположения, зафиксировать каждую группу расположений, выявить свойства и признаки объектов каждой группы; 2) найти в учебнике аналоги выявленных объектов и термины для их определения; 3) составить схемы определений; составить набор объектов для подведения под понятие; 4) сформулировать определения «открытых» понятий и сверить их с определениями в учебнике; 5) составить классификационную схему, родословную понятия
   Записать схему определения понятия в тетрадь, построить изображение объекта и его частных случаев (при необходимости)
   Контроль усвоения математического понятия: 1) Правильно ли названо имя понятия (термин)? 2) Правильно ли указан род понятия, является ли он ближайшим? 3) Остальные признаки понятия являются его существенными свойствами? 4) Не является ли число признаков избыточным? 5) Правильно ли построено предложение?
   Оценивание результатов выполненной деятельности: 1) Достигли ли вы поставленных целей УПД? 2) Какова была ваша активность на уроках? 3) Как вы оцениваете свою самостоятельность на уроках? 4) Что помогает вам быть самостоятельным? 5) Обращались ли вы за помощью к кому – либо? Почему? 6) Были ли вы внимательными на уроках? Что помогает вам быть внимательным? 7) Как вы осуществляете контроль своей учебной деятельности? 8) Что вы не усвоили? Почему? 9) Как бы вы хотели изменить свою учебную деятельность в будущем?
   Самодиагностика и коррекция собственных действий: 1) Зафиксировать своё внимание на ошибке и установить её характер; 2) Выполнить диагностику её причин – прежде всего в умственных действиях по применению теоретических положений; 3) Определить необходимость коррекционной меры; 4) Использовать откорректированные знания и действия в процессе решения аналогичных задач.

2. Структура саморегуляции УПД при освоении теорем^5

   Постановка учебной цели в процессе освоения теорем, выбор уровня достижения цели
   Репродуктивно - вариативный уровень (I)	Вариативно - эвристический уровень (II)	Эвристический уровень (III)
   Выявление объективной учебной информации, нужной для освоения теорем
   Соотнесение выявленной учебной информации с собственными знаниями и умениями; принятие решения об использовании помощи
   План деятельности при освоении теорем
   0) выполнить практическую работу по данному развёрнутому плану; попытаться сформулировать утверждение – гипотезу; 1) ознакомиться с формулировкой теоремы в учебнике; сверить формулировку со своим утверждением, если оно получено; выполнить анализ формулировки; 2) раскрыть термины понятий, данных в условии; 3) попытаться вывести следствия из условия теоремы; 4) вспомнить формулировки теорем, указанные в столбце «обоснования» данной таблицы; 5) попытаться вывести следствия из заключения теоремы; 6) рассмотреть готовую схему поиска доказательства теоремы и указать номера соответствующих обоснований, актуализированных в пункте 4; 7) прочитать доказательство теоремы в учебнике; 8) записать доказательство теоремы, используя приём и данную таблицу	0) выполнить практическую работу по данному краткому плану; попытаться сформулировать утверждение – гипотезу; 1) сверить своё утверждение с формулировкой теоремы в учебнике; выполнить анализ формулировки; 2) раскрыть термины понятий, данных в условии; 3) вывести следствия из условия теоремы; 4) вывести следствия из заключения теоремы; 5) попытаться заполнить пропуски в схеме поиска доказательства теоремы; 6) составить план доказательства, используя частично заполненную схему; 7) перечислить обоснования для каждого шага; 8) записать доказательство теоремы, используя приём и план, указанный в схеме поиска; 9) сравнить обоснования, указанные в доказательстве учебника и в своей записи доказательства; 10) сформулировать обратное утверждение, установить его истинность	0) используя определение данного понятия, зрительные впечатления, практические действия и др., сформулировать условное высказывание – гипотезу; 1) раскрыть термины понятий, данных в условии; 2) вывести следствия из условия высказывания; 3) вывести следствия из требования высказывания; 4) выполнить последовательный анализ заключения и условия, составляя схему поиска (при необходимости воспользоваться каркасом схемы поиска); 5) составить план доказательства и записать его; 6) сравнить число шагов в своей записи доказательства, с числом шагов, которые можно выделить в доказательстве учебника; 7) попытаться сформулировать идею доказательства; 8) сформулировать все виды утверждений и установить их истинность; 9) попытаться найти другие способы и методы доказательства
   Контроль усвоения теоремы: 1) Проверить правильность записи условия и требования теоремы; 2) Проверить правильность выполнения чертежа; 3) Проверить ход доказательства, правильно ли использован приём доказательства; 4) Проверить правильность и полноту обоснований; 5) Сформулировать идею доказательства теоремы; 6) Перечислить теоретические положения, которые использовались при доказательстве теоремы; 7) Рассказать план доказательства теоремы.
   Оценивание результатов выполненной деятельности: 1) Достигли ли вы поставленных целей УПД? 2) Какова была ваша активность на уроках? 3) Как вы оцениваете свою самостоятельность на уроках? 4) Что помогает вам быть самостоятельным? 5) Обращались ли вы за помощью к кому – либо? Почему? 6) Были ли вы внимательными на уроках? Что помогает вам быть внимательным? 7) Как вы осуществляете контроль своей учебной деятельности? 8) Что вы не усвоили? Почему? 9) Как бы вы хотели изменить свою учебную деятельность в будущем?
   Самодиагностика и коррекция собственных действий: 1) Зафиксировать своё внимание на ошибке и установить её характер; 2) Выполнить диагностику её причин – прежде всего в умственных действиях по применению теоретических положений; 3) Определить необходимость коррекционной меры; 4) Использовать откорректированные знания и действия в процессе решения аналогичных задач.

3. Структура саморегуляции УПД при решении задач^5

Постановка учебной цели в процессе решении задачи, выбор уровня достижения цели
Репродуктивно - вариативный уровень (I)	Вариативно - эвристический уровень (II)	Эвристический уровень (III)
Выявление объективной учебной информации, нужной для решения задачи
Соотнесение выявленной учебной информации с собственными знаниями и умениями; принятие решения об использовании помощи
План деятельности при решении задач выбранного уровня сложности
I. Работа с текстом задачи: выполнить анализ текста задачи; выполнить при необходимости чертёж; раскрыть термины понятий, данных в условии; записать данные и требование: «Дано»(«Найти», «Доказать»)
II. Поиск решения задачи: вывести следствия из условия задачи; вывести следствия из требования задачи; вывести следствия из условия и требования.
1) вспомнить формулировки теорем, указанные в столбце «обоснования» данной таблицы; 2) рассмотреть готовую схему поиска решения задачи и указать номера соответствующих обоснований, актуализированных в предыдущем пункте; 3) разобрать данное решение задачи и провести все рассуждения на аналогичной задаче	1) воспользоваться данным перечнем обоснований, необходимых для решения задачи; 2) заполнить пропуски в схеме поиска решения задачи; 3) если поиск решения задачи не закончен, то перейти на первый уровень самостоятельности	1) воспользоваться готовой идеей метода решения; 2) если поиск решения задачи не закончен, то перейти на второй уровень самостоятельности
III. Реализация плана решения:
1) выбрать способ записи решения; 2) выполнить правильную запись решения задачи, используя карточку информатор	1) выполнить полную правильную запись решения задачи своего уровня; 2) использовать сознательно способы неполной записи решения
IV. «Взгляд назад»:
Составить для своего уровня сложности задачи: по готовому чертежу и требованию, аналогичные, обратные задачи и решить их.	1) обобщить решение задачи одного типа; 2) составить задачи: по готовому чертежу без требования, аналогичные, обратные задачи и решить их	1) найти другие способы и методы решения; 2) составить задачи, используя все приёмы, и решить их; 3) составить приёмы решения задач одного типа
Контроль процесса решения задачи: объяснить решение задачи своего уровня сложности; 1) Проверить правильность записи условия и требования задачи; 2) Проверить правильность выполнения чертежа; 3) Проверить ход решения, правильно ли использован приём решения; 4) Проверить вычисления (если они есть); 5) Проверить правильность и полноту обоснований; 6) Проверить, рассмотрены ли частные случаи; 7) Проверить, проведено ли исследование (если необходимо); 8) Сформулировать идею решения; 9) Перечислить теоретические положения, которые использовались при решении задачи; 10) Рассказать план решения задачи.
Оценивание результатов выполненной деятельности: 1) Достигли ли вы поставленных целей УПД? 2) Какова была ваша активность на уроках? 3) Как вы оцениваете свою самостоятельность на уроках? 4) Что помогает вам быть самостоятельным? 5) Обращались ли вы за помощью к кому – либо? Почему? 6) Были ли вы внимательными на уроках? Что помогает вам быть внимательным? 7) Как вы осуществляете контроль своей учебной деятельности? 8) Что вы не усвоили? Почему? 9) Как бы вы хотели изменить свою учебную деятельность в будущем?
Самодиагностика и коррекция собственных действий: 1) Зафиксировать своё внимание на ошибке и установить её характер; 2) Выполнить диагностику её причин – прежде всего в умственных действиях по применению теоретических положений; 3) Определить необходимость коррекционной меры; 4) Использовать откорректированные знания и действия в процессе решения аналогичных задач.

1. Контрольные работы^11

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №1

Вариант 1

1. В ромбе ABCD угол между диагональю AC и стороной CD равен 35. Вычислите градусные меры углов ромба.

2. Периметр параллелограмма равен 30см. Одна из его сторон больше другой на 3 см. Вычислите длины сторон параллелограмма.

3. На диагонали MT прямоугольника KMPT отложены равные отрезки MA и TB. Докажите, что:

а) треугольники KMA и PTB равны;

б) четырехугольник KAPB является параллелограммом.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №1

Вариант 2

1. В ромбе MNPQ угол между диагональю MP и стороной PQ равен 55. Вычислите градусные меры углов ромба.

2. Периметр прямоугольника равен 36см. Одна из его сторон меньше другой на 8 см. Вычислите длины сторон прямоугольника.

3. Биссектрисы углов A и C параллелограмма ABCD пересекают его стороны BC и AD соответственно в точках E и F.

а) Докажите, что треугольники ABE и CDF равны;

б) Найдите длину отрезка EF, если AF=FD и периметр параллелограмма равен 48 см.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №1

Вариант 3

1. В ромбе KMPT угол между диагональю MT и стороной KM равен 25. Вычислите градусные меры углов ромба.

2. Периметр параллелограмма равен 48см. Одна из его сторон меньше другой в два раза. Вычислите длины сторон параллелограмма.

3. На продолжении диагонали AC прямоугольника ABCD отложены равные отрезки AM и CK. Докажите, что:

а) треугольники AMD и CKB равны;

б) четырехугольник MDKB является параллелограммом.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №1

Вариант 4

1. В ромбе ABCD угол между диагональю BD и стороной AD равен 75. Вычислите градусные меры углов ромба.

2. Периметр прямоугольника равен 72см. Одна из его сторон больше другой в три раза. Вычислите длины сторон прямоугольника.

3. Биссектрисы углов M и P параллелограмма MNPQ пересекают его стороны NP и MQ соответственно в точках A и B.

а) Докажите, что отрезки MA и PB равны;

б) Вычислите периметр параллелограмма MNPQ, если NA=AP и AB=12см.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №2

Вариант 1

1. Дано: NEPF.

Вычислите длину отрезка ME.

1. Диагонали параллелограмма равны 8см и 10см. Середины его сторон последовательно соединены отрезками.

а) Вычислите периметр образовавшегося четырёхугольника.

б) Определите вид образовавшегося четырехугольника. (Ответ поясните.)

1. Средняя линия равнобокой трапеции делится её диагоналями на отрезки, длины которых равны 7см, 4см и 7см. Диагональ трапеции делит её острый угол пополам. Вычислите:

а) длины оснований трапеции;

б) периметр трапеции.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №2

Вариант 2

1. Дано: MPNT.

Вычислите длину отрезка KM.

1. Диагональ прямоугольника равна 26см. Середины его сторон последовательно соединены отрезками.

а) Вычислите периметр образовавшегося четырёхугольника.

б) Определите вид образовавшегося четырехугольника. (Ответ поясните.)

1. Через вершину тупого угла С трапеции ABCD проведена прямая, параллельная боковой стороне AB. Эта прямая пересекает большее основание AD в точке К. Периметр трапеции равен 37см, DK=6см, AK=9см. Вычислите:

а) длину средней линии трапеции;

б) периметр треугольника KCD.

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №2

Вариант 3

1. Дано: AEBD.

Вычислите длину отрезка AB.

1. Диагональ квадрата равна 14дм. Середины его сторон последовательно соединены отрезками.

а) Вычислите периметр образовавшегося четырёхугольника.

б) Определите вид образовавшегося четырехугольника. (Ответ поясните.)

1. Средняя линия равнобокой трапеции равна 28см, а одно её основание – 24см. Диагональ трапеции делит её острый угол пополам.

Вычислите:

а) длину второго основания трапеции;

б) периметр трапеции.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Геометрия 8

КОНТРОЛЬНАЯ РАБОТА №2

Вариант 4

1. Д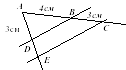ано: BDCE.

Вычислите длину отрезка DE.

1. Диагонали ромба равны 12см и 18см. Середины его сторон последовательно соединены отрезками.

а) Вычислите периметр образовавшегося четырёхугольника.

б) Определите вид образовавшегося четырехугольника. (Ответ поясните.)

1. Через вершину М трапеции KMPT (большее основание – KT) проведена прямая, параллельная боковой стороне PT. Эта прямая и основание KT пересекаются в точке Е. Периметр KME равен 17см, MP=7см, KE=4см. Вычислите:

а) длину средней линии трапеции;

б) периметр трапеции.

1. Глосаррий

Параллелограмм

Определение: Параллелограммом называется ____________________

____________, у которого ____________________________________

стороны ___________________________________, т.е. _____________

_________ на ___________________________________ прямых.

Признак параллелограмма 1: Если диагонали четырёхугольника ____

______________________ и точкой ______________________ делятся __________________________, то он является ___________________.

Признак параллелограмма 2: Если у четырёхугольника две стороны _

______________________________ и ______________________, то он является __________________________________.

Признак параллелограмма 3: Если у четырёхугольника противолежащие стороны _______________________________ , то он является

__________________________________.

Свойство диагоналей параллелограмма: Диагонали параллелограмма

________________________ и точкой ___________________________ делятся __________________________.

Свойство противолежащих сторон параллелограмма: Противолежащие стороны параллелограмма ___________________.

Свойство противолежащих углов параллелограмма: Противолежащие углы параллелограмма ________________________.

Свойство биссектрисы угла параллелограмма: Биссектриса угла параллелограмма отсекает от него ______________________________

_____________ треугольник.

Свойство биссектрис противолежащих углов параллелограмма: Биссектрисы противолежащих углов параллелограмма ____________

__________________________.

Прямоугольник

Определение: Прямоугольник – это _____________________________

____________, у которого _____________ углы __________________.

Признак прямоугольника 1: Если у параллелограмма ______________ углы ________________, то он является ________________________.

Признак прямоугольника 2: Если у параллелограмма _____________

________________ угол ________________________, то он является

______________________________.

Признак прямоугольника 3: Если у параллелограмма диагонали_____

_________________, то он является ____________________________.

Признак прямоугольника 4: Если у четырёхугольника _____________ угла ________________________, то он является _________________

__________________.

Свойство диагоналей прямоугольника 1: Диагонали прямоугольника _____________________.

Свойство диагоналей прямоугольника 2: Диагонали прямоугольника при _______________________________ делят его на ______________

__________________________________ треугольника.

Ромб

Определение: Ромб – это ___________________________________, у которого __________________ стороны ________________________.

Признак ромба 1: Если у параллелограмма диагонали _____________

_____________________, то он является ________________________

Признак ромба 2: Если у параллелограмма диагональ является _____

___________________________ его углов, то он является __________.

Признак ромба 3: Если у четырёхугольника все стороны __________, то он является ______________________________________________.

Свойства диагоналей ромба 1, 2: Диагонали ромба _________________

________________________________________. Диагонали ромба являются ________________________________ его _________________.

Свойство диагоналей ромба 3: Точка пересечения диагоналей ромба

равноудалена от его _______________.

Квадрат

Определение 1: Квадрат – это прямоугольник, у которого __________

____________________________________________________________

Определение 2: Квадрат – это ромб, у которого ___________________

____________________________________________________________

Признак квадрата 1: Если у прямоугольника диагонали ___________

__________________ под ________________________________углом, то он является _______________________________________________

Признак квадрата 2: Если у ромба _____________ угол ___________

_______, то он является ______________________________________.

Теорема Фалеса: Если _____________________________ прямые, пересекающие ___________________ угла, отсекает на ___________ его стороне ________________ отрезки, они отсекают ________________ отрезки и на _____________ его стороне.

Средняя линия треугольника

Определение: Средней линией треугольника называется ___________ ___________________________________________________________.

Свойство средней линии треугольника: Средняя линия треугольника, соединяющая середины ___________ данных ___________________, __________________________ третьей ________________________ и _____________________ её ________________________.

Трапеция

Определение: Трапецией называется четырёхугольник, у которого __ _______________________ две _________________________________ стороны ____________________________________. Эти ___________ ____________________________ стороны называются ___________ ________________. Две другие стороны называются ______________ _________________ сторонами.

Равнобокая трапеция

Определение: Трапеция, у которой ___________________________ стороны ____________________ называется _____________________ ______________. Трапеция, у которой ___________________________ стороны __________________________________ называется _______ ________________________.

Свойство углов равнобокой трапеции: У равнобокой трапеции углы при _________________________________________.

1 свойство диагоналей равнобокой трапеции: У равнобокой трапеции диагонали ________________________.

2 свойство диагоналей равнобокой трапеции: Если у равнобокой трапеции боковая сторона равна меньшему ______________________ ________, то диагонали являются ______________________________ ___________________ острых углов.

1 признак равнобокой трапеции: Если у трапеции углы при основании ___________, то она является _____________________________.

2 признак равнобокой трапеции: Если у трапеции диагонали _______ ____________, то она является _____________________________.

3 признак равнобокой трапеции: Если у трапеции диагонали являются ________________________________ острых _______________, то она является _____________________________.

Средняя линия трапеции

Определение: Отрезок, _______________________________ середины __________________________ сторон называется средней линией трапеции.

Свойство средней линии трапеции: Средняя линия трапеции _______ _______________________________ основаниям и ________________ их _____________________________.

Теорема о пропорциональных отрезках: _________________________ _______ прямые, пересекающие ___________________ угла, отсекают от ___________________ угла __________________________________ отрезки.

Построение четвертого пропорционального отрезка

Дано: b

c

d

Построить:

Построение:

1. Самостоятельная работа №2^12

ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Вариант А1

1. Диагональ ромба образует с одной из его сторон угол 20°. Найдите углы ромба.

2. Диагонали прямоугольника пересекаются под углом 20°. Найдите углы, которые образует диагональ со сторонами прямоугольника.

3. Докажите, что если диагонали ромба равны, то он является квадратом.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Вариант А2

1. Сторона ромба образует с одной из диагоналей угол 50°. Найдите углы ромба.

2. Диагональ прямоугольника образует с одной из его сторон угол 40°. Найдите острый угол, образующийся при пересечении диагоналей данного прямоугольника.

3. Докажите, что если диагонали прямоугольника перпендикулярны, то он является квадратом.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Вариант Б1

1. Сторона ромба образует с его диагоналями углы, один из которых в 4 раза больше другого. Найдите углы ромба.

2. Диагональ делит угол прямоугольника в отношении 2:7. Найдите углы между диагоналями данного прямоугольника.

3. На диагонали AC квадрата ABCD отложены отрезки AM и CN. Докажите, что BNDM – ромб.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Вариант Б2

1. Диагонали ромба образуют с его сторонами углы, один из которых на 50° меньше другого. Найдите углы ромба.

2. Углы, образовавшиеся при пересечении диагоналей прямоугольника, относятся как 2:7. Найдите углы, которые образует диагональ со сторонами данного прямоугольника.

3. На продолжении диагонали AC квадрата ABCD отложены отрезки AM и CN. Докажите, что BNDM – ромб.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Вариант В1

1. Высота ромба, проведенная из вершины тупого угла, делит сторону ромба пополам. Найдите углы ромба.

2. В прямоугольнике ABCD биссектриса угла А образует с диагональю BD углы, один из которых равен 105°. Найдите острый угол между диагоналями прямоугольника.

3. Докажите, что середины сторон квадрата являются вершинами другого квадрата.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Вариант В2

1. В ромбе ABCD биссектриса угла АBD проходит через середину стороны AD. Найдите углы ромба.

2. В прямоугольнике ABCD биссектриса угла А образует с диагональю АС угол 20°. Найдите тупой угол между диагоналями прямоугольника.

3. На сторонах квадрата ABCD от вершин B и D отложены равные отрезки BK, BM, DN и DP. Докажите, что точки K, M, N и P являются вершинами прямоугольника.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Опорные конспекты

Геометрия 8

Средняя линия треугольника (теория)

Определение: Средней линией треугольника называется ___________

___________________________________________________________.

Средняя линия треугольника отрезок EF; E – середина AB; F – середина BC.

Свойство средней линии треугольника: Средняя линия треугольника, соединяющая середины ___________ данных ___________________, __________________________ третьей ________________________ и _____________________ её ________________________.

Д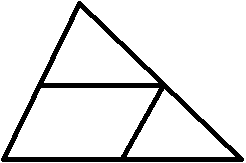ано: PAC, NCD,

PN – _______________________________ACD.

Доказать: PN  _____, PN = AD : 2.

Доказательство:

дополнительное построение: RN  _____, RN∩AC=R;

NK – _______________________________ACD, KAD.

Утверждение

Обоснование

1. N – ___________________ CD 2. CN = _____ 3. RN  _____ 4. R – ___________________ AC 5. P – ___________________ AC 6. P и R совпадают 7. PN  _____ 8. NK  ____ 9. APNK – ___________________ 10. PN = _____ 11. K – __________________ AD 12. AK =_____ = _______ : 2 13. PN = AD : 2

по _________________________ средней линии треугольника N – ___________________ CD по _________________________ по теореме __________________ по _________________________ средней линии треугольника по пунктам ___ и ___ по пункту ___ и построению по доказанному по _________________________ параллелограмма по свойству _________________ ____________параллелограмма по _________________________ средней линии треугольника K – __________________ AD по пунктам ___ и ___

ч.т.д.

Задача №55: Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма.

Дано: _________ – четырёхугольник;

__, __, __, __ – середины ____, ____, ____, ____.

Доказать: ____________ – параллелограмм.

Доказательство:

1) _____ – средняя линия _______ (по _________________________)

_____ – средняя линия _______ (по _________________________)

2) ____  ____ _____ и ______ = _______ = _______ : 2 ( по ________

_____________ средней линии треугольника)

3) ____________ – параллелограмм (по _______________________)

ч.т.д.

Геометрия 8

Признаки равнобокой трапеции (теория)

Определение: Трапеция, у которой _________________________ стороны _________________ называется _______________________________.

1 признак равнобокой трапеции: Если у трапеции углы при основании ___________, то она является _____________________________.

Дано: MNEF – _______________________; M =  ___;

MF и _____ – __________________.

Доказать: MNEF – _______________________ трапеция

Доказательство:

дополнительное построение: NH  _____, NH∩____ = ___.

Утверждение

Обоснование

1. NH  _____ 2. F =  ______ 3. M =  ___ 4. M =  ______ 5. MNH – ___________________ 6. MN = _____ 7. MF  _____ 8. NHFE – __________________ 9. EF =______ 10. ______ = _____ 11. MNEF – __________________ трапеция

по _________________________ по свойству _____________ при ____________________ прямых по _________________________ по пунктам ___ и ___ по _________________________ равнобедренного треугольника по _________________________ равнобедренного треугольника по _________________________ трапеции по _________________________ по свойству _________________ ____________параллелограмма по пунктам ___ и ___ по _________________________ ____________________трапеции

ч.т.д.

2 признак равнобокой трапеции: Если у трапеции диагонали ____________, то она является _____________________________.

Дано: HKPS – _______________________; HP = _____;

HS и _____ – __________________.

Доказать: HKPS – _______________________ трапеция.

Доказательство: дополнительное построение: KMHS, PNHS.

Утверждение	Обоснование
1. HS  ____	по __________________________ трапеции
2. KM  PN 3. MKPN – ___________________ 4. KM = _____ 5. HP = _____ 6. HPN =  _______ 7. PHN = _____ 8. HS – _______________________ 9. PHS =  _______ 10. PS = ____ 11. HKPS – ____________________ трапеция	по __________________________ параллельности по __________________________ по свойству __________________ _____________________________ по __________________________ по катету и гипотенузе у равных _____________________ _______________________ равны по __________________________ по ___ признаку у равных _____________________ _______________________ равны по ___________________________ _____________________ трапеции

ч.т.д.

3 признак равнобокой трапеции: Если у трапеции диагонали являются _______ ______________ острых _______________, то она является _________________.

Дано: EFPS – _______________________;

ES и _____ – ____________________;

EP – ________________________  _______;

___ – ________________________  _______.

Доказать: EFPS – _______________________ трапеция.

Доказательство:

Утверждение	Обоснование
1. ES  _____ 2. FPE = _______ PFS = _______ 3. FEP = _______ PSF = _______ 4. _______ = _______ _______ = _______ 5. EFP – ____________________ FPS – ____________________ 6. ______ = FP = ______ 7. EFPS – _____________________ трапеция	по ___________________________ трапеции по свойству _______________ при ______________________ прямых по __________________________ _____________________________ по пунктам ___ и ___ по __________________________ _________________ треугольника по __________________________ равнобедренного треугольника по ___________________________ _____________________ трапеции

ч.т.д.