Разработка элективного занятия по теме " Элементарные функции: свойства и графики"

Муниципальное бюджетное общеобразовательное учреждение –

Средняя общеобразовательная школа р. п. Пушкино

Советского района Саратовской области

Интегрированное элективное занятие

«Элементарные функции: свойства и графики»

(математика и информатика)

Для учащихся 10 – 11 классов.

Выполнили: Беляева Н. В.

учитель математики и информатики

Исингалиева М. К.

учитель математики

Интегрированное элективное занятие

«Элементарные функции: свойства и графики»

(математика и информатика)

Величие человека - в его способности мыслить.

(Б. Паскаль)

Используемые формы педагогической деятельности:

активизация знаний и внимания, беседа, деятельность в группе, создание учебных познавательных и коммуникативных ситуаций.

Используемые педагогические технологии:

технология критического мышления, технология проектной деятельности.

Тема занятия: Построение и преобразование графиков элементарных функций.

Тип занятия: обобщение и систематизация знаний по теме «Элементарные функции и их графики».

Формы работы на уроке: фронтальная, групповая, индивидуальная

Цели:

Образовательные:

Повторение теоретического материала и построение графиков элементарных функций с использованием программ «Advanced Grapher 2.2» и «Master Function 2.0»

Продолжать внедрение компьютерных технологий в процесс обучения математике, показать интеграцию двух предметов: математики и информатики.

Формировать навыки использования компьютерных технологий на уроках математики

Развивающие:

Развивать познавательный интерес учащихся

Развивать умения анализировать, сравнивать, выделять главное, приводить примеры

Воспитательные: Способствовать выработке у школьников умения обобщать изучаемые факты; развивать самостоятельность путем выполнения компьютерного эксперимента.

Техническое обеспечение:

ПК с программным обеспечением «Advanced Grapher 2.2», «Master Function 2.0»

Мультимедиа проектор

Презентации по теме «Элементарные функции, преобразование графиков»

Структура занятия.

Ход занятия:

1. Организационный момент. Приветствие.

Здравствуйте, ребята! Мы рады сотрудничать с вами.

Настроены ли Вы на работу? Тогда в добрый путь! Улыбнемся друг другу!

Вы любите слушать музыку? А какую музыку вы предпочитаете? Мы предлагаем вам послушать классическую музыку и просмотреть слайды. (фрагмент в исполнении Ванессы Мэй)

Вы уже догадались, какова тема сегодняшнего элективного занятия?

Мы предлагаем провести с вами занятие математики и информатики по теме «Элементарные функции: свойства и графики».

Перед нами стоит цель: повторить свойства элементарных функций и способы преобразования их графиков.

1. Актуализация знаний.

Фронтальный опрос

Просмотр презентации по теме с комментариями и устными заданиями

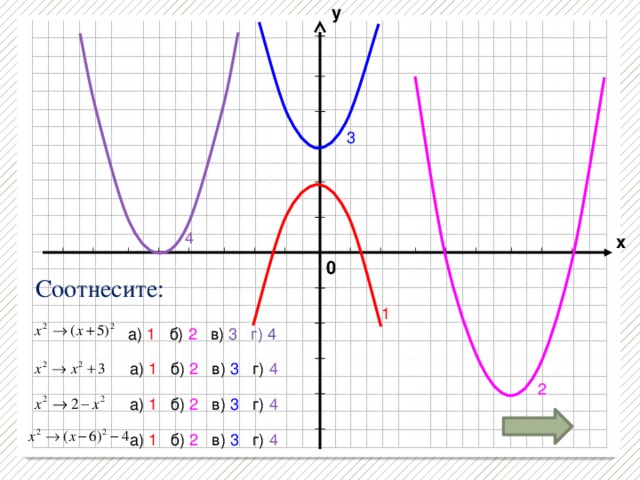
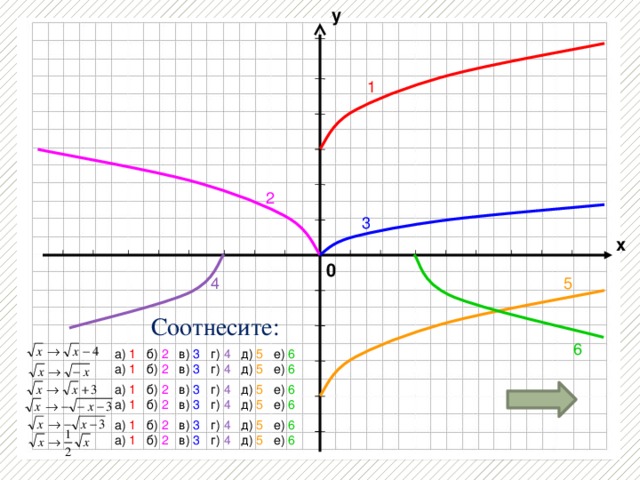
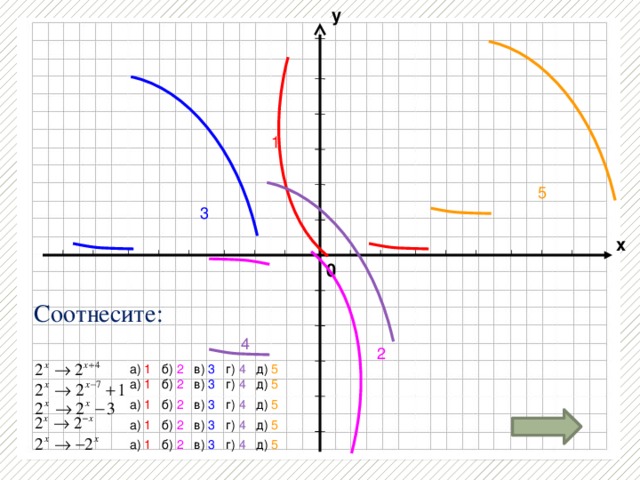
1. Творческое задание по группам:

Каждая группа получает на карточке задание и демонстрирует ответ у доски

1группа - Распознать и построить график функции по описанию

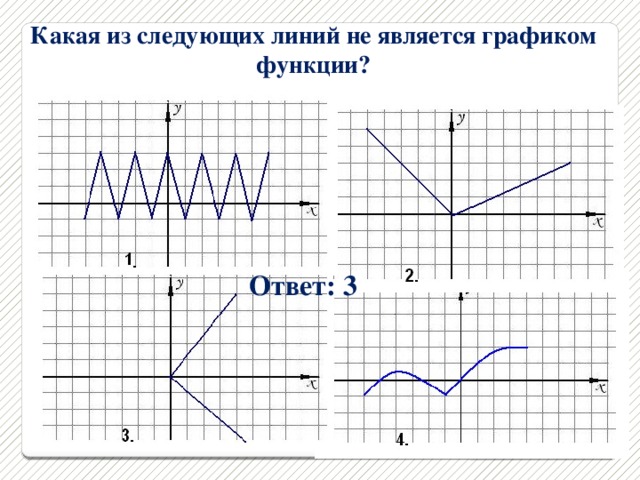
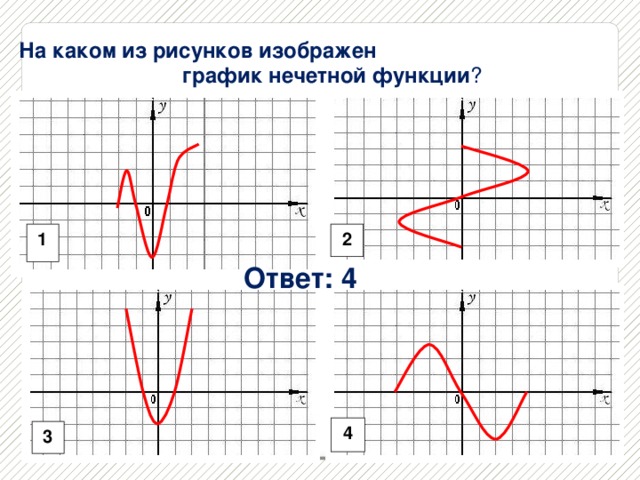
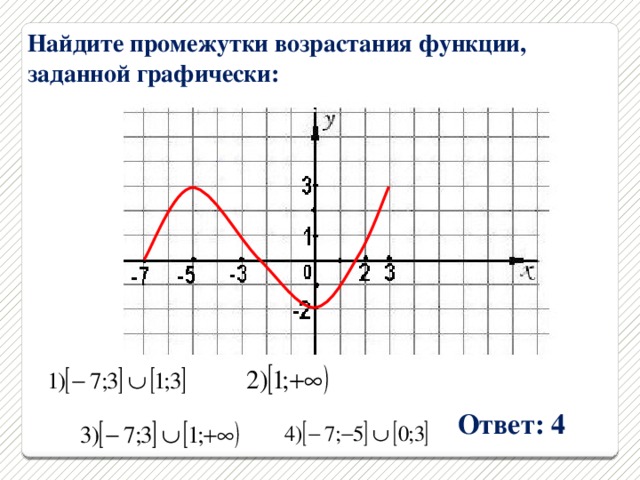
2 группа - По графику функции составить её словесное описание.

4. Конструктивный тест

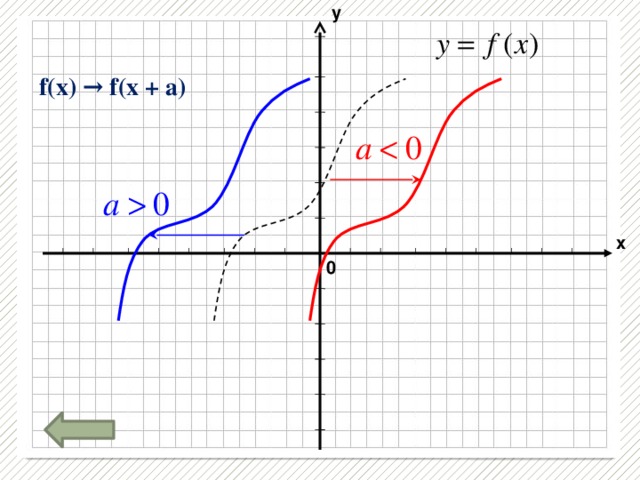
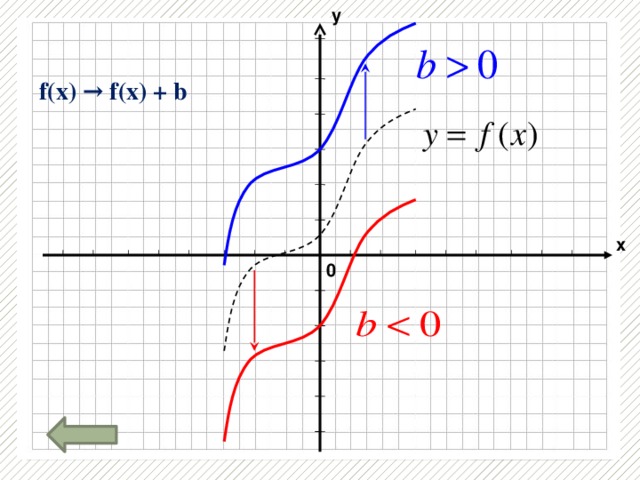
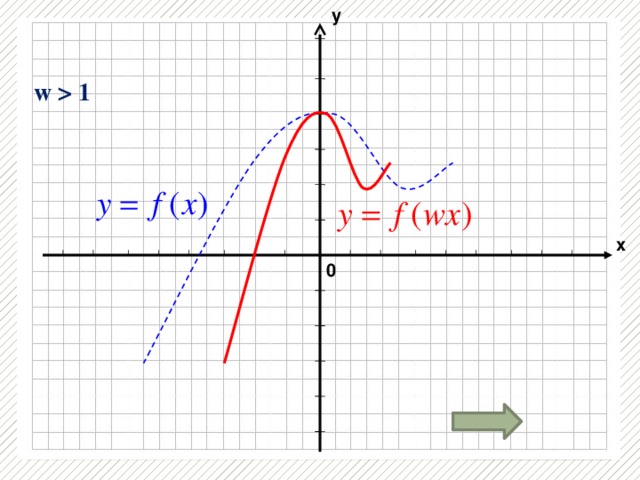
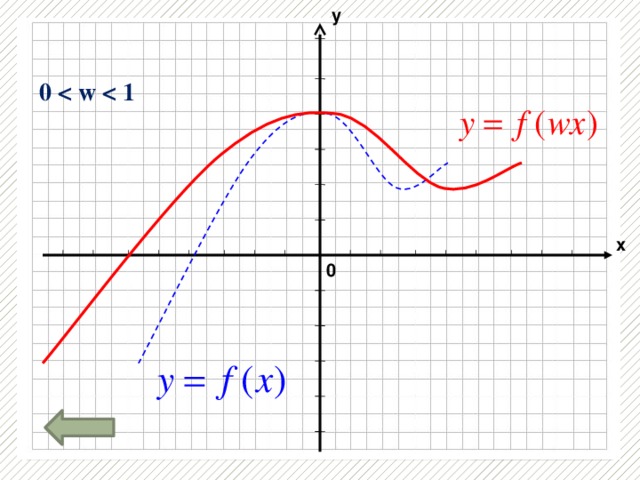
Презентация «Преобразование графиков функции »

Повторить виды преобразований графиков функций и выполнить тест.

Проверить результаты теста и поставить себе оценку. (Ответы на интерактивной доске.)

5. Знакомство с возможностями программ «Advanced Grapher 2.2» и «Master Function 2.0»

Н. Е. Жуковский сказал: “В математике есть своя красота, как в живописи и поэзии”. Сегодня на элективном занятии мы научимся простому и красивому методу построения графиков элементарных функции.

Практические работы можно поставить иначе: не от математической модели, созданной учителем, к результату, а, наоборот, от поставленной задачи - к созданию учеником математической модели.

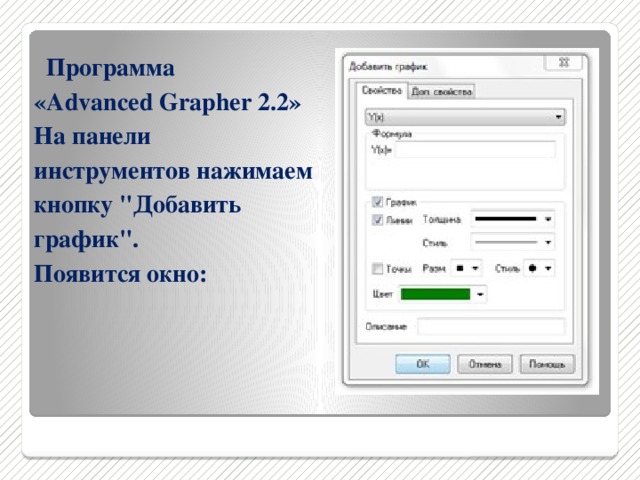
Построить график практически любой функции по формуле в этих программах несложно. Программа «Advanced Grapher 2.2» С помощью программы «Advanced Grapher 2.2» можно строить графики функций, уравнений и неравенств по формулам и с помощью таблицы. Выбор осуществляется кнопками на панели инструментов: добавить график или добавить график таблицы. На панели инструментов нажимаем кнопку "Добавить график". Появится окно:

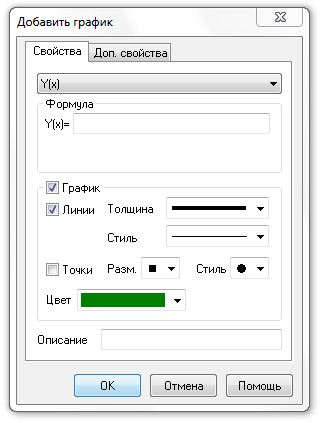
Первая строка определяет зависимость одной неизвестной в формуле от другой. По умолчанию это зависимость у=у(х), поэтому ничего не изменяем.

Во второй строке записывается формула. Некоторые правила записи:

1. Записи выполняются в английской раскладке клавиатуры.

2. Степень записывается знаком ^2. Двойка означает, что вторая степень.

3. Умножение можно записывать без какого-либо знака или знаком *, деление - знаком / .

4. Аргумент у функций, которые записываются в буквенном виде, записывается в скобках.

5. В десятичных дробях вместо запятой пишется точка.

Если формула будет записана с ошибкой, программа сразу предупредит об этом. Полный список функций, которые поддерживает «Advanced Grapher2.2» можно увидеть в руководстве пользователя, открыв в программе вкладку "Помощь".

Сохранение построенных графиков.

Сохранить построенные графики можно в виде рисунков и в виде файлов графика формата AGR. Графики (изображения координатной плоскости) можно сохранять в виде рисунков - в файлы в форматах GIF, BMP и EMF, а также копировать в буфер обмена в форматах EMF и BMP. Формат EMF является векторным, поэтому он является предпочтительным для обмена с теми программами, которые в дальнейшем будут масштабировать рисунок (например, Microsoft Word).

1. «Master Function 2.0»

Программа для построения графиков и анализа функций. Автор Гришин Александр. Сайт автора: http://masterfunction.narod.ru/.

Интерфейс программы интуитивно-понятный.

В версии 2.0 реализованы следующие возможности:

Построение графиков функций любой сложности.

Возможность отыскания производной в текстовом виде.

Построение касательных.

Построение касательных и нормалей.

Вычисление значения определенного интеграла.

Таблица значений функции в разных точках.

Построение графика линейной функции по двум точкам.

Построение графика параболы по известным точкам.

Решение квадратных уравнений.

Программа позволяет одновременную работу с 16 функциями. Возможны различные преобразования координатной плоскости.

Цель обучения состоит в том, чтобы сделать ученика способным развиваться дальше без помощи учителя. Э. Хаббард

6. Исследовательская работа на компьютерах.

Класс делится на несколько групп для исследовательской работы.

Каждой группе выдается карточка с заданием, учащиеся работают над поставленной проблемой, строят графики и проводят их преобразование с помощью программы «Advanced Grapher2.2» и готовятся к устному выступлению.

7. Физминутка

8. Задания для самостоятельной исследовательской работы:

1 группа

Постройте графики функций данного вида и проследите, как изменяется вид графика в системе координат:

1. y=lnx, y=lnx+5, y=ln(x+3), y=|ln(x+3)-7|, y=ln(x+5);

2. y=x², y=x²-6, y=x²-3x+2, y=|x²-3x+2|, y=2|x²-11|;

3. y=3^x, y=3^x+3, y=|3^x-15|, y=3^x-|5+x|.

На основе полученных результатов сделать соответствующие выводы о преобразованиях графиков данных функций.

2 группа

Постройте графики функций данного вида и проследите, как изменяется вид графика в системе координат:

a) y=lgx, y=lgx+3, y=lg(x+5), y=|lg(x+3)-6|, y=|lg(x+3)|;

b) y=x³, y=x³-6, y=x³-3x²+2x-1, y=|x³-3x²+2x|-1, y=3|x³-5|;

c) y=2^x, y=2^x+3, y=|2^x-5|, y=2^x-|7+x|.

На основе полученных результатов сделать соответствующие выводы о преобразованиях графиков данных функций.

3 группа

Постройте графики функций данного вида и проследите, как изменяется вид графика в системе координат:

1. y=lgx, y=lg(x+2), y=lg(3x-7), y=|lg(x+2)|-7, y=|lg(3x-7)|;

2. y=x²+4x-5, y=x ^|2+4x|-6, y=|x²+4x|-5, y=|x^2+4x-6|, y=|x²+4x-5|;

3. y=5^x, y=5^x+3, y=|5^x-11|, y=5^x-|5+x|.

На основе полученных результатов сделать соответствующие выводы о преобразованиях графиков данных функций.

4 группа

Постройте графики функций данного вида и проследите, как изменяется вид графика в системе координат:

1. y=lnx, y=lnx-7, y=ln(x+4), y=|ln(x+4)-7|, y=|ln(x+4)|;

2. y=x², y=|x²-6|, y=x²-3x+2, y=|x²-3x+2|, y= |x²-3x|+2;

3. y=3^x, y=3^x+2, y=|3^x-6|, y=3^x-|5+x|, y=3^x-6.

На основе полученных результатов сделать соответствующие выводы о преобразованиях графиков данных функций.

2.Демонстрация результатов

С помощью локальной сети и мультимедийного проектора группы демонстрируют результаты своей работы, делают выводы.

Другие учащиеся записывают результаты исследований и выводы в тетрадь.

9. Рефлексия (цветовая) и итоги занятия

Постройте график функции у=2x² одним из следующих цветов, которые на ваш взгляд соответствуют вашему настроению от проделанной работы:

Красный – отличное;

Зеленый – хорошее;

Синий – удовлетворительное.

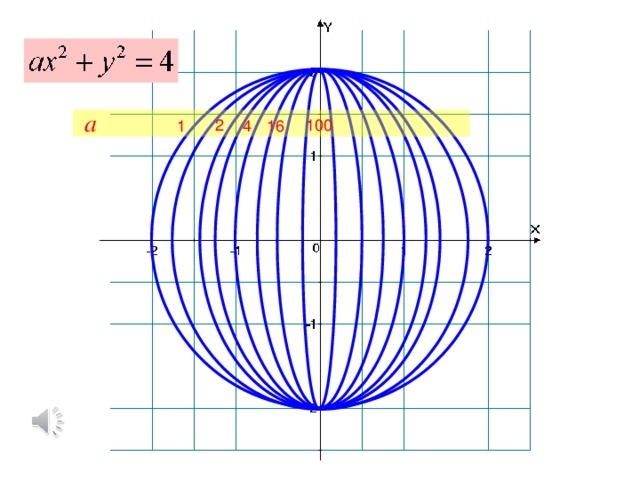
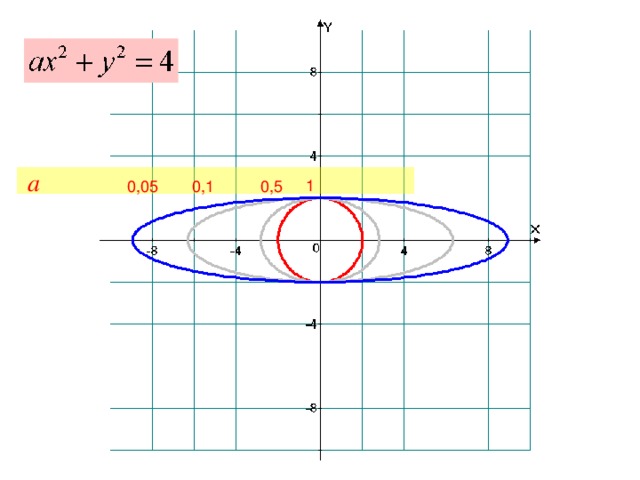
Сегодня на уроке вы исследовали математические модели графиков функций с помощью компьютерных программ «Advanced Grapher 2.2» и «Master Function 2.0».

Муниципальное бюджетное общеобразовательное учреждение –

Средняя общеобразовательная школа р. п. Пушкино

Советского района Саратовской области

Интегрированное занятие

«Элементарные функции:

свойства и графики»

(математика и информатика)

Выполнили: Беляева Н. В.

учитель математики и информатики

Исингалиева М. К.

учитель математики

а

100

2

1

16

4

а

1

0,05

0,5

0,1

а

= 0

b

10

0,6

-0,5

-50

1

0,4

0,02

0,8

0,06

0,08

-10

-0,2

-0,1

5

2

-100

0,1

-5

-1

0,04

-0,05

20

0

-2

Величие человека –

в его способности мыслить.

(Б. Паскаль)

Цель занятия:

• Повторение свойств элементарных функций и способов преобразований их графиков;
• знакомство с возможностями программного обеспечения «Advanced Grapher 2.2» и «Master Function 2.0»;
• Компьютерный эксперимент: «Построение и преобразование графиков элементарных функций с помощью данной программы.

2.Что называется графиком функции?

1. Что такое функция?

3. Какая функция называется возрастающей (убывающей)?

4 . Какая функция называется четной (нечетной)?

5. Каким свойством обладает график четной (нечетной) функции? последний вопрос)

Графики элементарных функций школьного курса

Линейная функция

Квадратичная функция

Степенная функция

Дробно-линейная функция

Функция , где

Показательная функция

Логарифмическая функция

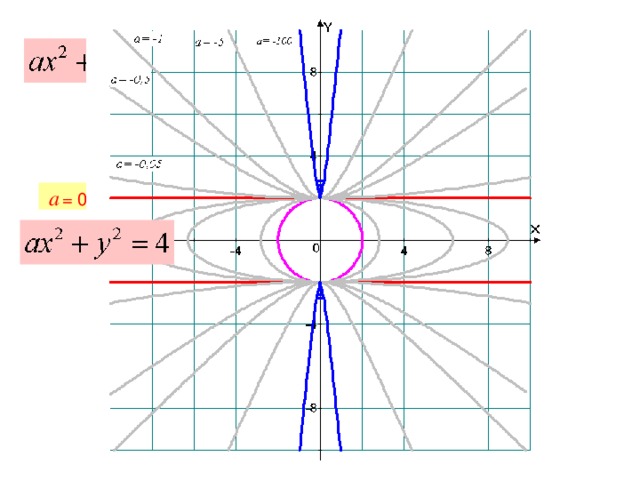
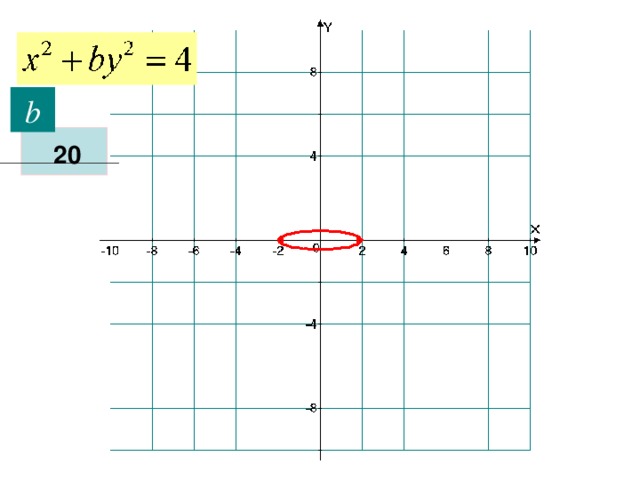
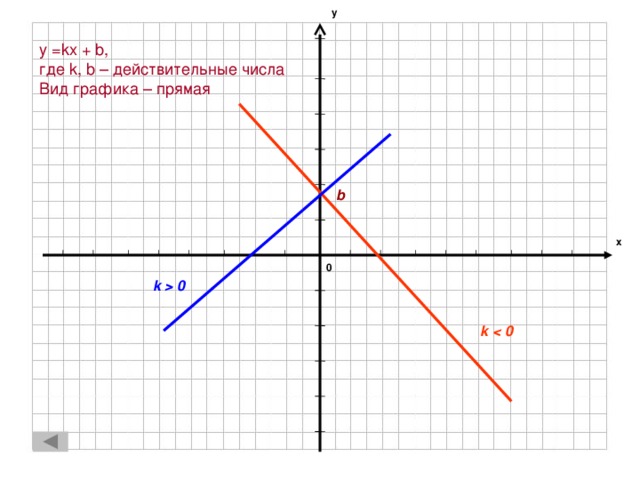0 k" width="640"

у

y =kx + b, где k, b – действительные числа Вид графика – прямая

b

х

0

k 0

k

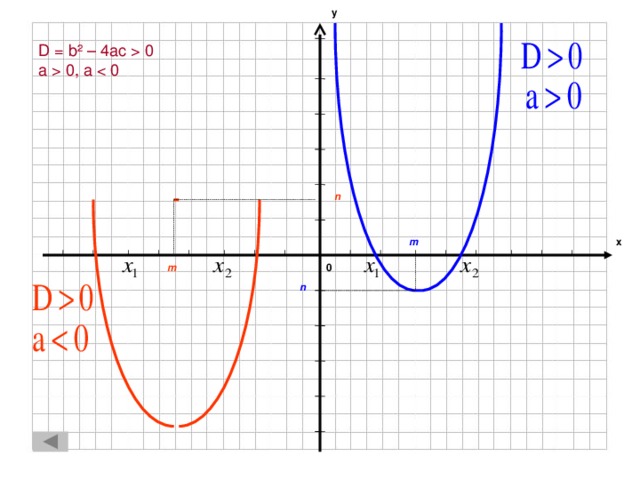0 a 0, a n х m m 0 n" width="640"

у

D = b² – 4ac 0 a 0, a

n

х

m

m

0

n

у

n – чётное

1

х

-1

0

1

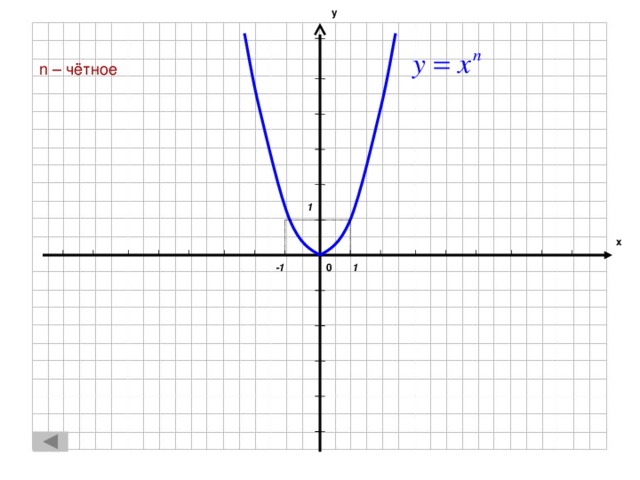
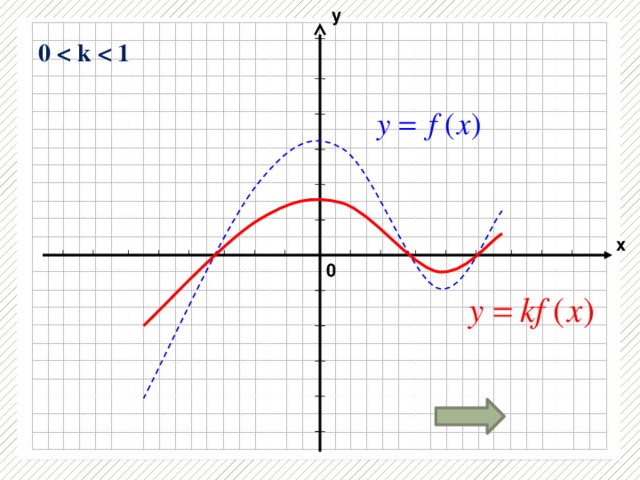
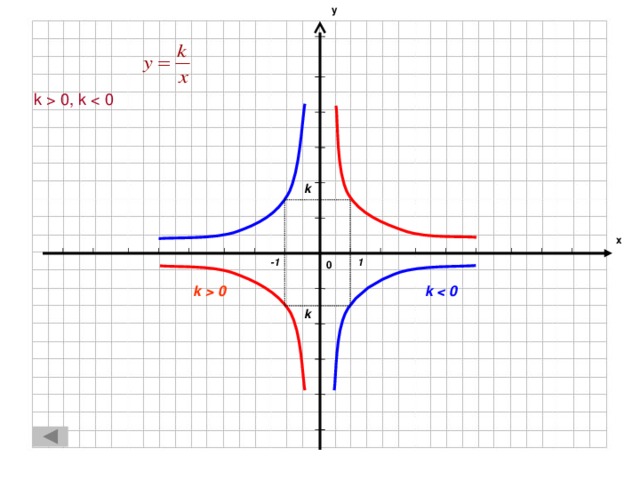0, k k х -1 1 0 k k 0 k" width="640"

у

k 0, k

k

х

-1

1

0

k

k 0

k

у

n – чётное

1

х

1

0

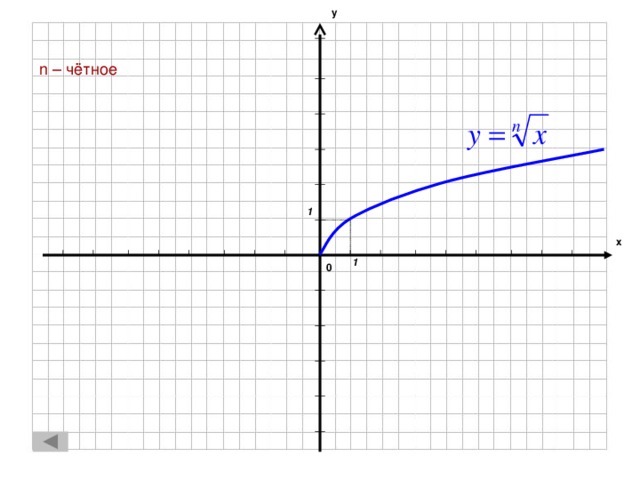
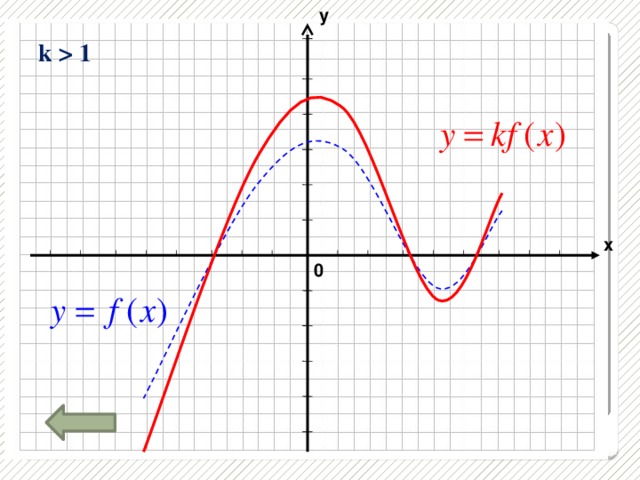
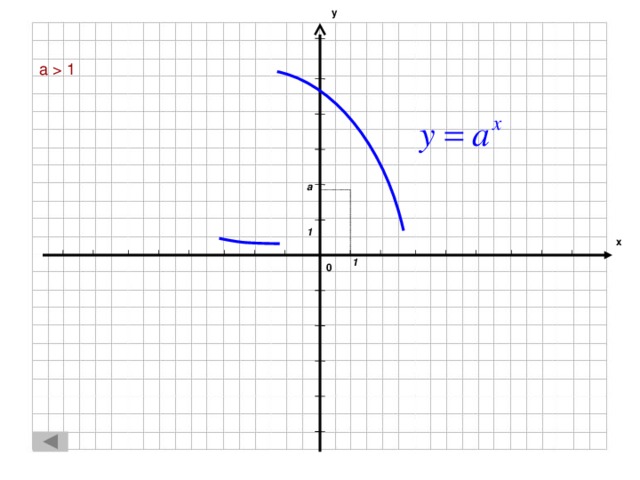1 a 1 х 1 0" width="640"

у

a 1

a

1

х

1

0

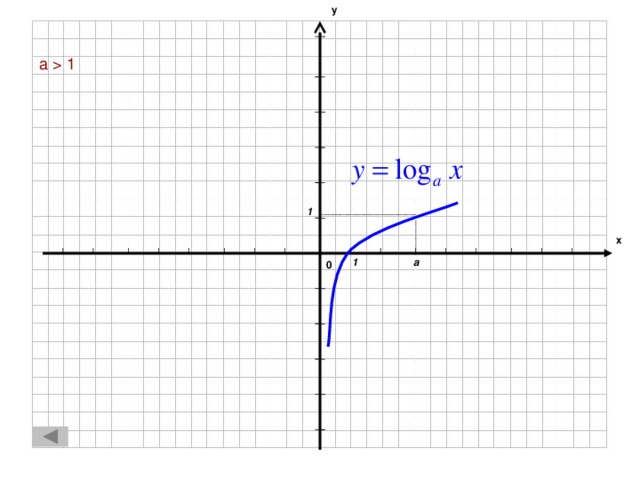1 1 х a 1 0" width="640"

у

a 1

1

х

a

1

0

Какая из следующих линий не является графиком функции?

Ответ: 3

График какой функции изображен

на рисунке?

Ответ: 2

Укажите все нули функции, график которой изображен на рисунке?

Ответ: 3

На каком из рисунков изображен график нечетной функции ?

1

2

Ответ: 4

4

3

Множество значений функции, изображенной

на рисунке, есть промежуток ….

Ответ: 2

Укажите график четной функции

Ответ: 4

Сколько точек минимума имеет функция,

заданная графиком на отрезке

Ответ: 2

Найдите промежутки возрастания функции,

заданной графически:

Ответ: 4

Изобразите «портрет» функции

по заданным свойствам :

1.Это четная функция

2.Ее область определения

3.Ее область значений

4. У нее 2 точки минимума и 1 точка максимума

5. На промежутке

она имеет 4 нуля,

среди которых 1 и 5.

6.

7.Один из промежутков возрастания

на промежутках

8.

Основные приёмы преобразования графиков

Преобразование симметрии относительно оси абсцисс

Преобразование симметрии относительно оси ординат

Параллельный перенос вдоль оси абсцисс

Параллельный перенос вдоль оси ординат

Растяжение и сжатие вдоль оси абсцисс

Растяжение и сжатие вдоль оси ординат

Построение графика функции у =│f(x)│

Построение графика функции у = f(│x│)

Построение графика функции у = │f(│x│)│

у

f(x) → – f (x)

х

0

у

f(x) → f(– x)

х

0

у

f(x) → f(x + а)

х

0

у

f(x) → f(x) + b

х

0

1 х 0" width="640"

у

w 1

х

0

у

0

х

0

у

0

х

0

1 х 0" width="640"

у

k 1

х

0

у

f(x) → │f(x)│

х

0

у

f(x) → f(│x│)

х

0

у

f(x) →│f(│x│)│

х

0

Несколько последовательных преобразований графика функции

f(x) → f(│x│) →│f(│x│)│

• f(x) = x² – 6x + 8 = (x – 3)² – 1
• f(│x│) = (│x│– 3)² – 1
• │ f(│x│)│=│(│x│– 3)² – 1│

у

f(x) → f(│x│) →│f(│x│)│

х

-2

-3

3

-4

2

4

0

-1

f(x) = x² – 6x + 8 = (x – 3)² – 1

f(│x│) = (│x│– 3)² – 1

│ f(│x│)│=│(│x│– 3 )² – 1│

Проверь себя.

у

3

4

х

0

Соотнесите:

1

а) 1 б) 2 в) 3 г) 4

а) 1 б) 2 в) 3 г) 4

2

а) 1 б) 2 в) 3 г) 4

а) 1 б) 2 в) 3 г) 4

у

1

2

3

х

0

4

5

Соотнесите:

6

а) 1 б) 2 в) 3 г) 4 д) 5 е) 6

а) 1 б) 2 в) 3 г) 4 д) 5 е) 6

а) 1 б) 2 в) 3 г) 4 д) 5 е) 6

а) 1 б) 2 в) 3 г) 4 д) 5 е) 6

а) 1 б) 2 в) 3 г) 4 д) 5 е) 6

а) 1 б) 2 в) 3 г) 4 д) 5 е) 6

у

1

5

3

х

0

Соотнесите:

4

2

а) 1 б) 2 в) 3 г) 4 д) 5

а) 1 б) 2 в) 3 г) 4 д) 5

а) 1 б) 2 в) 3 г) 4 д) 5

а) 1 б) 2 в) 3 г) 4 д) 5

а) 1 б) 2 в) 3 г) 4 д) 5

Молодец!

Молодец!

Молодец!

Не огорчайся. Попробуй ещё раз!

Не огорчайся. Попробуй ещё раз!

Не огорчайся. Попробуй ещё раз!

Н. Е. Жуковский говорил:

«В математике есть своя красота, как в живописи и поэзии»

Программа «Advanced Grapher 2.2» На панели инструментов нажимаем кнопку "Добавить график". Появится окно:

Некоторые правила записи: 1. Записи выполняются в английской раскладке клавиатуры. 2. Степень записывается знаком ^2. Двойка означает, что вторая степень. 3. Умножение можно записывать без какого-либо знака или знаком *, деление - знаком / . 4. Аргумент у функций, которые записываются в буквенном виде, записывается в скобках. 5. В десятичных дробях вместо запятой пишется точка.

Пример записи

Алгебраическое выражение

Пример записи для ввода в программу

 

2х+3

2х+3

x 2 -5х+6

x^2-5*x+6

X 5

X^5

2:x

2/x

2 x

℮ x

2^x

lnx

еxp(x)

ln(x)

lgx

lg(x)

√ x

sgrt(x)

|x|

abs(x)

³√x

x^ 1/3

Программа «Master_function 2.0»

Интерфейс программы интуитивно-понятный.

Панель инструментов:

В версии 2.0 реализованы следующие возможности:

Построение графиков функций любой сложности.

Возможность отыскания производной в текстовом виде.

Построение касательных.

Построение касательных и нормалей.

Вычисление значения определенного интеграла.

Таблица значений функции в разных точках.

Построение графика прямой по двум точкам.

Построение графика параболы по известным точкам.

Решение квадратных уравнений.

Цель обучения состоит в том, чтобы сделать ученика способным развиваться дальше без помощи учителя. Э. Хаббард

Используемые источники:

• [email protected]
• http:// www.valeryzykin.ru/view_journal.php?id=11
• http:// www.valeryzykin.ru/view_page.php?id=1
• http:// www.valeryzykin.ru/view_journal.php?id=18
• http:// www.valeryzykin.ru/view_journal.php?id=16