Рабочая программана год кружка по математике для 5 класса. Конспекты занятий и презентации к ним на 1 четверть.

МБОУСОШ станицы Терской Моздокского района РСО-Алания

Рабочая программа

кружка

" Гимнастика ума"

для учащихся 5 классов

Учитель Яшина Н.П.

2015-2016учебный год

Пояснительная записка.

Основная задача обучения математике в школе - обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества.

Для активизации познавательной деятельности учащихся, развития прочных вычислительных навыков и поддержания интереса к математике вводится курс «Гимнастика ума», способствующий развитию навыков устного счёта с использованием рациональных приёмов, математического мышления, а также эстетическому воспитанию ученика, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм.

В детстве ребенок открыт и восприимчив к чудесам познания, к богатству и красоте окружающего мира. У каждого из них есть способности и таланты, надо в это верить, и развивать их.

Актуальность программы определена тем, что школьники должны иметь мотивацию к обучению математике, стремиться развивать свои интеллектуальные возможности.

Данная программа позволяет учащимся ознакомиться со многими интересными вопросами математики на данном этапе обучения, выходящими за рамки школьной программы, расширить целостное представление об этой науке.

Решение математических задач, связанных с логическим мышлением, изучение рациональных приёмов устного счёта закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию.

Не менее важным фактором реализации данной программы является и стремление развить у учащихся умений самостоятельно работать, думать, решать творческие задачи, а также совершенствовать навыки аргументации собственной позиции по определенному вопросу.

Занятия математического кружка должны содействовать развитию у детей математического образа мышления: краткости речи, умелому использованию символики, правильному применению математической терминологии и т.д.

Творческие работы, проектная деятельность и другие технологии, используемые в системе работы кружка, должны быть основаны на любознательности детей, которую следует поддерживать и направлять.

Кружок создается на добровольных началах с учетом склонностей ребят, их возможностей и интересов.

Срок реализации данной программы кружка – 1 учебный год. Занятия 1 раз в неделю. Продолжительность каждого занятия не должна превышать 40 минут.

Принципы программы:

Актуальность

Создание условий для повышения мотивации к обучению математики, стремление развивать интеллектуальные возможности учащихся.

Научность

Математика – учебная дисциплина, развивающая умения логически мыслить, видеть количественную сторону предметов и явлений, делать выводы, обобщения.

Системность

Курс строится на переходе от частных примеров (особенности решения отдельных заданий) к общим (решение математических задач).

Практическая направленность.

Решение задач, встречающихся в реальной жизни.

Цели обучения.

• Развитие логического и алгоритмического мышления.

• Знакомство с приёмами рационального счёта и доведение их до автоматизма.

• Создание ситуации « погружения» в нетрадиционные задачи.

• Выработка навыков устной монологической речи.

• Создание дидактических материалов для устной работы на уроке.

• Создание условий для эффективной групповой и индивидуальной учебной деятельности, способствующей наиболее полной реализации потенциальных познавательных возможностей всех детей в целом и каждого ребенка в отдельности, принимая во внимание особенности их развития.

Ожидаемые результаты.

Личностными результатами изучения курса

является формирование следующих умений:

• определять и высказывать под руководством педагога самые простые общие для всех людей правила поведения при сотрудничестве (этические нормы).

• знать приёмы быстрого устного счёта и пользоваться ими на практике

• уметь самостоятельно составлять дидактические карточки по изучаемой теме, составлять магические квадраты, ребусы, кроссворды.

Для оценки формирования и развития личностных характеристик учащихся используется:

• наблюдение,

• математические игры,

• опросники,

• анкетирование

Метапредметными результатами изучения курса является

формирование универсальных учебных действий (УУД).

Для отслеживания уровня усвоения программы и своевременного внесения коррекции использовать следующие формы контроля:

• занятия-конкурсы на повторение практических умений,

• занятия на повторение и обобщение (после прохождения основных разделов программы),

• самопрезентация (просмотр работ с их одновременной защитой ребенком),

• участие в математических олимпиадах и конкурсах различного уровня.

Кроме того, необходимо систематически отмечать:

• результативность и степень самостоятельности деятельности ребенка,

• активность при создании творческих работ (карточки, ребусы, кроссворды, презентации)

Содержание программы.

Тематическое планирование занятий

Рациональные приёмы

1. *Умножение на 9 на пальцах

2. *Использование переместительного и сочетательного свойств сложения и умножения.

3. * Сложение и вычитание суммы и разности двух одинаковых чисел.

4. *Использование распределительного свойства умножения относительно сложения и вычитания

1. *Умножение на11, 111, ….

2. *Умножение на 22, 33, 44 и т.д.

3. *Умножение на 101, 1001, 10001…

4. Умножение на 5, 50, 25, 75, 125

5. Умножение двузначных чисел от10 до 20: (14*19=(19+4)*10+4*9=230+36=266

6. Возведение в квадрат двузначных чисел, оканчивающихся на 5.

7. Возведение в квадрат двузначных чисел, имеющих 5 десятков (53²=2809, к 25+3=28, приписать квадрат числа единиц, чтобы получилось четырёхзначное число)

8. Умножение чисел, количество десятков которых одинаково, а сумма единиц равна 10 (24*26; 37*33)

9. Умножение двузначных чисел, близких к 100 (с недостатком)

10. Умножение чисел, близких к 100 (с избытком)

11. Умножение крестом.

12. Умножение на 37 и деление на 37.

13. Возведение в квадрат чисел 11, 111, 1111 и т.д.

14. Способ округления при сложении, вычитании и умножении.

15. Способ изменения множителей в одно и то же число раз или изменение делимого и делителя

16. Умножение чётных чисел на числа, оканчивающиеся цифрой 5 (чётный множитель разделить на 2, а другой умножить на 2)

1.Числа и вычисления (11 ч.).

Римская и древнерусская системы исчисления. Правила быстрого счета. Числовые ребусы. Магические квадраты.

2.Геометрические фигуры (3 ч.)

Треугольник. Четырехугольники. Геометрические задачи. Пространственные фигуры.

3.Ребусы. Кроссворды (5 ч.)

Знакомство с ребусами и их составление. Кроссворды.

4.Логические задачи (7 ч.)

Числовые мозаики. Задачи со спичками.Судоку.

5.Решение задач (8 ч.)

Занимательные и шутливые задачи. Задачи на доказательство от противного. Задачи на движение.

Тематическое планирование.

Номер занятий Содержание занятий Количество часов

I. Числа и вычисления. 11 часов

1-2. Римская нумерация. 2 часа

3. Древнерусская система счисления. 1 час

4-5. Правила и приемы быстрого счета. 2 часа

6. Конкурс «Кто быстрее сосчитает». 1 час

7-8. Знакомство с числовыми ребусами. 2 часа

9. Решение и составление числовых ребусов. 1 час

10. Магические квадраты 1 час

11. Заключительное занятие «Путешествие в страну чисел». 1 час

II.Геометрические фигуры. 3 часа

12. Треугольник, задачи с треугольниками. 1 час

13. Четырехугольники. Геометрические головоломки. 1 час

14. Заключительное занятие «Занимательная геометрия». 1 час

III.Ребусы. Кроссворды. 5 часов

15. Знакомство с принципами их составления. 1 час

16. Решение и составление ребусов. 1 час

17. Знакомство с кроссвордами. 1 час

18. Составление и решение кроссвордов. 1 час

19. Конкурс на лучший ребус и кроссворд. 1 час

IV.Логические задачи. 7 часов

20. Знакомство с числовыми мозаиками. 1 час

21. Составление и решение числовых мозаик. 1 час

22. Решение и составление задач со спичками. 1 час

23. Головоломки со спичками. 1 час

24. Задачи на переливание жидкостей. 1 час

25. Знакомство с судоку. Решение судоку . 1час

26. Заключительное занятие «Математический КВН». 1 час

V.Решение задач. 8 часов

27. Решение занимательных задач. 1 час

28. Решение шутливых задач. 1 час

29. Задачи на доказательство от противного. 1 час

30. Задачи на движение. 1 час

31-32. Приключения на тропинках математики 2 час

33. Старинные задачи. 1 час

34. Вечер «Занимательная математика». 1 час

Литература.

1. Галкин Е.В. Нестандартные задачи по математике: Задачи логического характера: Кн. для учащихся 5-11 кл. М.: Просвещение; Учебная литература, 1996 г.

1. Свечников А.А., Сорокин П.И. Числа, фигуры, задачи по внеклассной работе. Пособие для учителей. М.: Просвещение, 1999 г.

1. Белоусов В.М. Занимательная стандартизация. Очерки. С.-П.: Детская литература, 1998

1. Коваленко В.Г. Дидактические игры на уроках математики: Кн. для учителя. – М.: Просвещение, 2000 г.

1. Игнатьев Е.И. В царстве смекалки. – М.: Наука. Главная редакция физико-математической литературы, 1979 г.

1. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4-8 кл. сред.шк. – 5е изд. – М.: Просвещение, 1998 г.

1. Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и контрольных работ по математике для 6 класса. – М.: Илекса, Харьков: Гимназия, 1998 г.

1. Перельман И. «Живая математика». М. Изд. «Наука», 1974г.

2. Штейнгауз Г. Сто задач: Пер. с пол. – 4-е изд. – М.: Наука. Гл.ред. физ.-мат.лит.,1996г.

Кружок «Гимнастика ума» для учащихся 5 класса

МБОУСОШ станицы Терской

Моздокского района РСО-Алания

Учитель Яшина Н.П.

2015-2016 учебный год, I четверть

Первое занятие

• Вводное занятие. Цели и задачи кружка.
• Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Освоение вычислительных навыков развивает память и помогает усваивать предметы математического цикла. Существует много приемов упрощения арифметических действий. Знание упрощенных приемов вычисления особенно важно в тех случаях, когда ученик не имеет в своем распоряжении таблиц и калькулятора.
• Правила и приёмы вычислений не зависят от того, выполняются они письменно или устно. Однако, владение навыками устных вычислений представляет большую ценность не потому, что в быту ими пользуются чаще, чем письменными выкладками. Это важно ещё и потому, что они ускоряют письменные вычисления, приобретают опыт рациональных вычислений, дают выигрыш в вычислительной работе, развивают память, гибкость ума, смекалку.

Картина Николая Петровича Богданова-Бельского

«Устный счёт»

(1895 год)

Учитель народной школы Сергей Александрович Рачинский

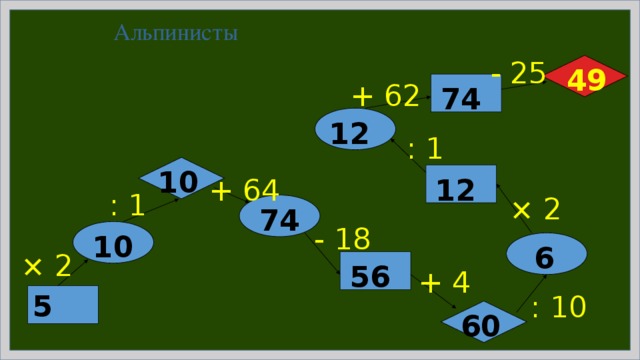
Альпинисты

- 25

49

+ 62

74

12

: 1

10

12

+ 64

: 1

× 2

74

- 18

10

6

× 2

56

+ 4

: 10

5

60

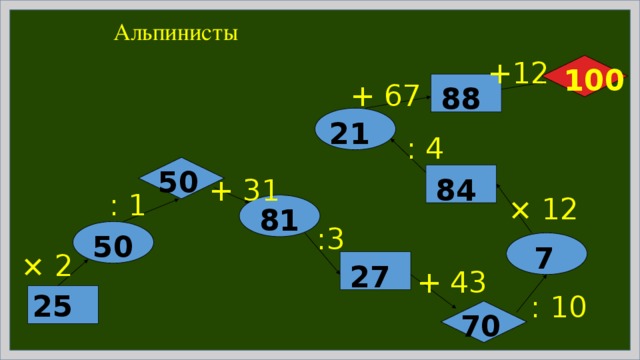
Альпинисты

+12

100

+ 67

88

21

: 4

50

84

+ 31

: 1

× 12

81

:3

50

7

× 2

27

+ 43

: 10

25

70

Математические цепочки

360

640

+ 280

: 4

160

× 18

20

245

10

- 55

- 370

× 2

190

380

Математические цепочки

640

810

+ 170

: 90

9

× 16

40

298

90

- 68

- 370

× 2

230

460

Викторина «О математике с улыбкой»

Что является «нулем» на карте железных дорог России?

Н.Н.Коломина

Москва: по железным дорогам России все расстояния считаются от Москвы, кроме Октябрьской железной дороги, где отсчет идет от Санкт-Петербурга.

Н.Н.Коломина

Чтобы научиться быстро считать, надо обязательно знать:

• Таблицу

сложения и вычитания

в пределе 20.

• Таблицу

умножения и деления в пределе 100

Занятие второе

Счёт на пальцах

Способ быстрого умножения чисел в пределах первого десятка на 9.   Допустим, нам нужно умножить 7 на 9.

Повернём руки ладонями к себе и загнём седьмой палец (начиная считать от большого пальца слева).

Число пальцев слева от загнутого будет равно десяткам, а справа - единицам искомого произведения.

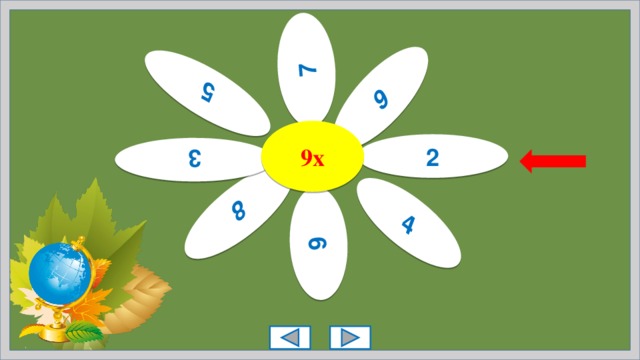
9

7

5

8

4

3

6

9х

2

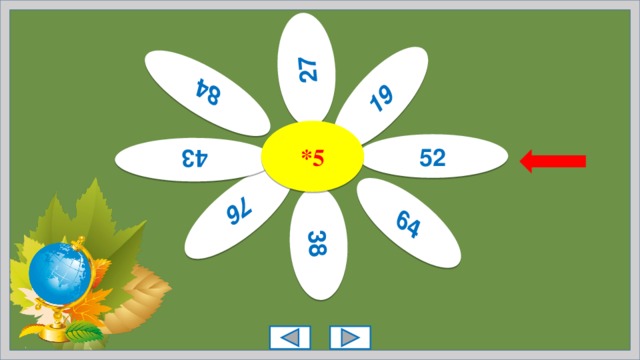
19

27

84

76

64

43

38

*5

52

Викторина «О математике с улыбкой»

Названия многих русских городов произошли от числительных: Семипалатинск, Семилуки, Пятигорск. А какой город был назван в честь числа 10000?

Н.Н.Коломина

Тюмень, от тюркского слова

«тумен» – 10 000.

В старину на Руси число 10000 называли «тьма». Военачальника, который командовал войском в 10000 воинов, называли темником.

Н.Н.Коломина

Рациональные приёмы устных вычислений

Способ группировки слагаемых так, чтобы получить круглое число

Третье занятие

Способ группировки

• Этот способ применяют в тех случаях, когда слагаемые при их группировке дают в сумме круглые числа, полученные результаты потом складывают.
• Например:
• 74+32+67+48+33+26=(74+26)+(32+48)+(67+33)=
• =100+80+100=280

Вычислить, используя способ группировки

• а) 229+148+286+352+471+114=
• =(229+471)+(148+352)+(286+114)=
• =700+500+400=1600.

• б) 1208+34+31+792+166+19=
• =(1208+792)+(34+166)+(31+19)=
• =2000+200+50=2250.

• в) 171+825+354+175+246+229=
• =(171+229)+(825+175)+(354+246)=
• =400+1000+600=2000

Способ перестановки множителей и их группировка.

• Этот способ применяют тогда, когда произведение двух множителей является круглым числом.

• Важно помнить!

Замечательные пары чисел:

• 100 – это:

10*10; 20*5; 25*4; 50*2.

• 1000 – это:

500 *2; 250*4; 125*8; 200*5

• Вычислить:

• а) 250*168*4; 362*20*5;
• б) 125*25*8*4; 200*472*5;
• в) 4*8*75*125; 25*8+125*16;
• г) 25*16-125*3; 125*24-1998;
• д) 1000-125*32; 500*79*2-399.

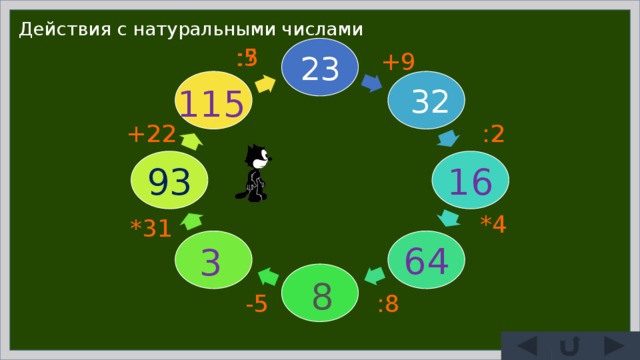
Действия с натуральными числами

:5

:?

+9

23

32

115

:2

+22

93

16

*4

*31

64

3

8

-5

:8

Действия с натуральными числами

:3

:?

*2

16

32

48

*3

-52

100

96

:8

*25

12

4

84

:21

*7

Математическая викторина

Назовите «математические» растения, в названии которых

есть число.

Н.Н.Коломина

Тысячелистник, столетник, золототысячник.

Н.Н.Коломина

Вычитание суммы из числа и числа из суммы

Четвёртое занятие

Объяснение

• а) Чтобы из числа вычесть сумму,

можно поочерёдно (удобным способом)

вычесть каждое слагаемое:

96-(49+26)=96-26-49=70-49=21.

• б) Чтобы из суммы вычесть число,

можно это число вычесть из одного (удобного)

слагаемого, а к полученному результату

добавить второе слагаемое:

(72+87)-52=72-52+87=20+87=107.

Вычитание суммы из числа и числа из суммы

*а) 198-(79+88)=

=198-88-79=

=110-79=31

*б) 472-(152+297)=

=472-152-297=

=320-297=23

*в) (324+286)-196=

=324+(286-196)=

=324+90=414

* г) (721+525)-680=

= (721-680)+525=

=41+525=566

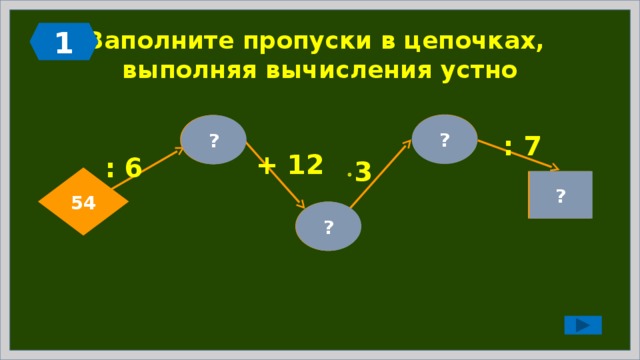
1

Заполните пропуски в цепочках, выполняя вычисления устно

63

?

9

?

: 7

+ 12

: 6

 3

54

?

9

21

?

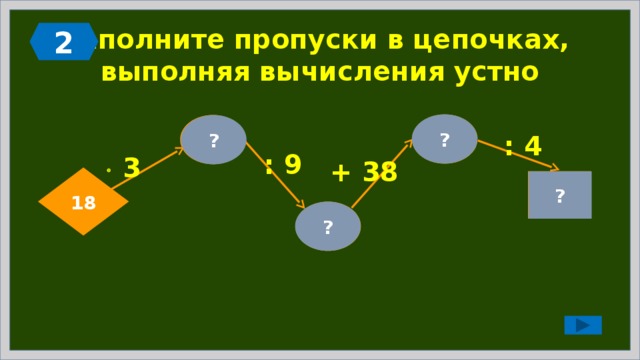
2

Заполните пропуски в цепочках, выполняя вычисления устно

?

44

54

?

: 4

: 9

 3

+ 38

18

11

?

6

?

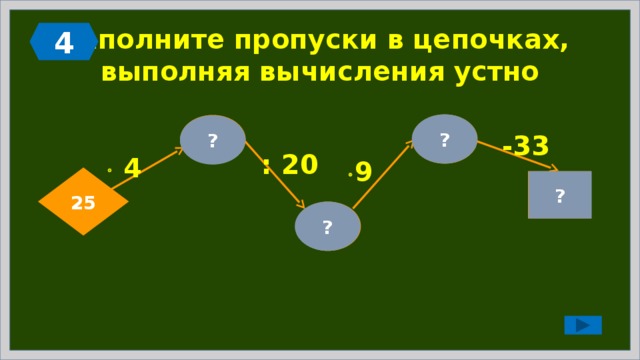
4

Заполните пропуски в цепочках, выполняя вычисления устно

?

45

100

?

-33

: 20

 4

 9

25

?

12

5

?

5

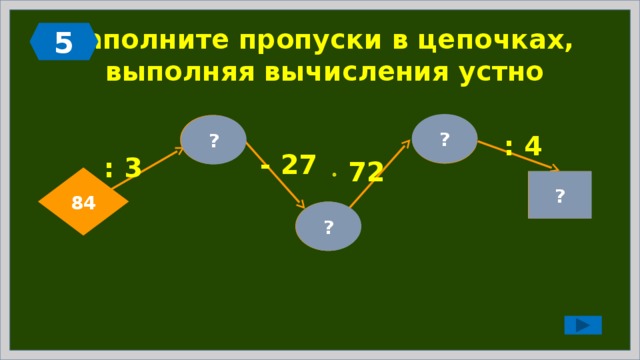
Заполните пропуски в цепочках, выполняя вычисления устно

?

72

28

?

: 4

- 27

: 3

 72

84

?

18

1

?

6

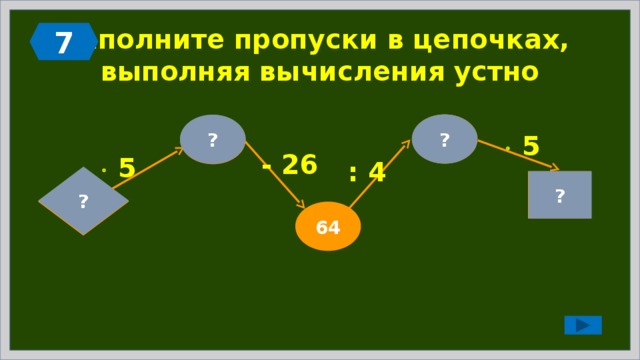
Заполните пропуски в цепочках, выполняя вычисления устно

?

16

?

100

- 16

- 4

+ 18

: 6

?

82

0

?

96

7

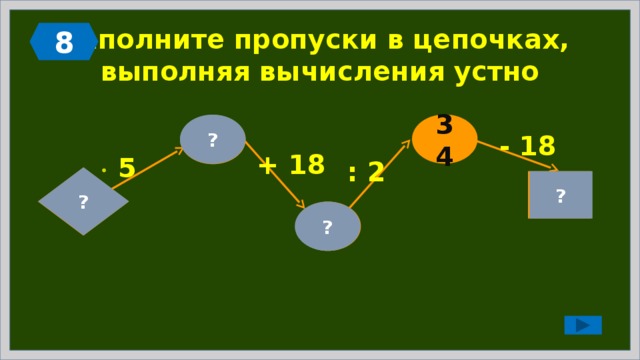
Заполните пропуски в цепочках, выполняя вычисления устно

?

16

?

90

 5

- 26

 5

: 4

?

18

?

80

64

8

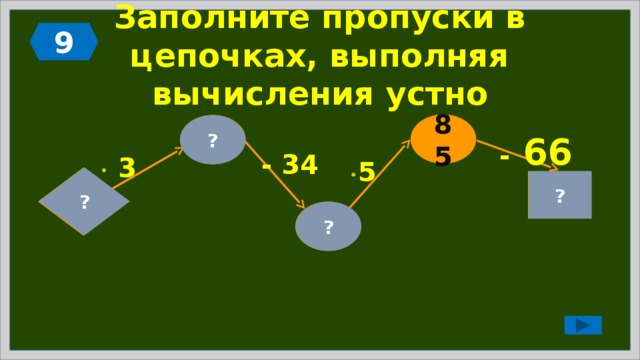
Заполните пропуски в цепочках, выполняя вычисления устно

34

?

50

- 18

+ 18

 5

: 2

?

10

?

16

68

?

9

Заполните пропуски в цепочках, выполняя вычисления устно

85

51

?

- 66

- 34

 3

 5

?

17

?

19

17

?

10

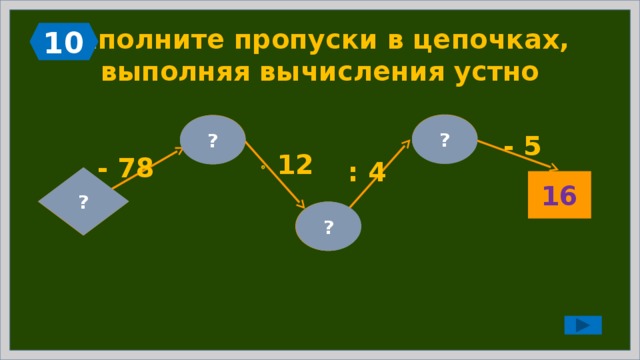
Заполните пропуски в цепочках, выполняя вычисления устно

21

?

7

?

- 5

 12

- 78

: 4

?

85

16

84

?

11

Заполните пропуски в цепочках, выполняя вычисления устно

?

3

54

?

 11

- 12

 2

: 14

?

27

33

42

?

12

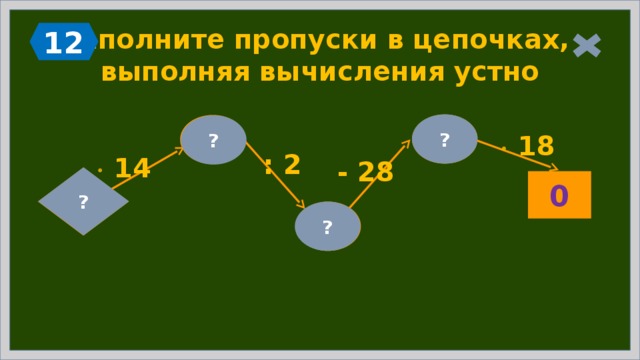
Заполните пропуски в цепочках, выполняя вычисления устно

?

0

56

?

 18

: 2

 14

- 28

?

4

0

28

?

Рациональный приём сложения и вычитания суммы и разности двух одинаковых чисел

Пятое занятие

(a+b)+(a-b); (a+b)-(a-b)

• Объяснение

• Пусть надо вычислить:
• а) (8+5)+(8-5)=13+3=16 (это 2*8 )
• (14+9)+(14-9)=23+5=28 (это2*14)

• Вывод: Если к сумме двух чисел прибавить разность этих же чисел, то в результате получится удвоенное большее число.

• Объяснение

• Пусть надо вычислить:
• б) (8+5)-(8-5)=13-3=10 (это2*5)
• (14+9)-(14-9)=23-5=18 (это 2*9)

• Вывод : Если из суммы двух чисел вычесть разность этих же чисел, то в результате получится удвоенное меньшее число.

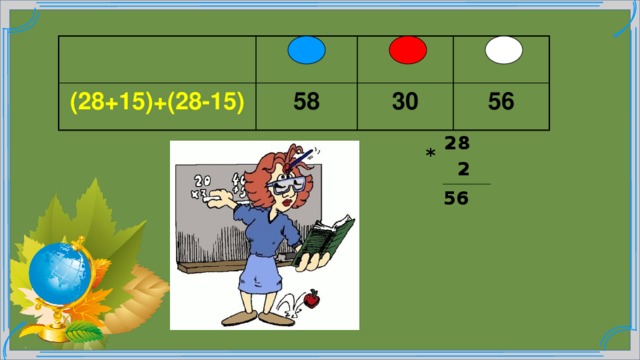
(28+15)+(28-15)

58

30

56

28

2

*

56

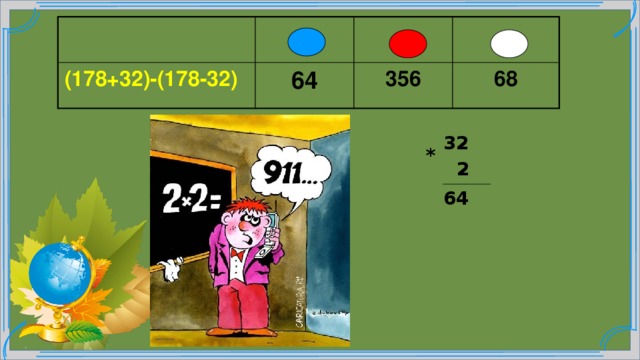
(178+32)-(178-32)

64

356

68

32

2

*

64

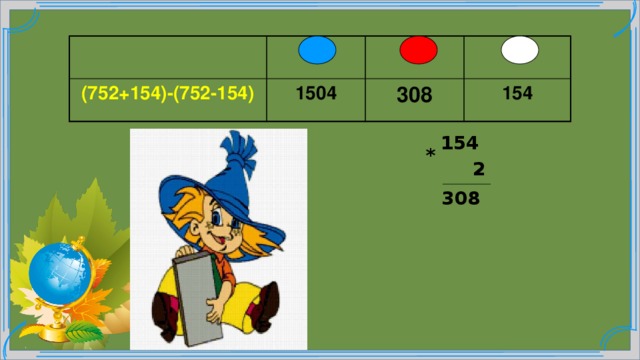
(752+154)-(752-154)

1504

308

154

154

2

*

308

(298-179)+(298+179)

596

358

298

298

2

*

596

(452-268)+(268+452)

336

1004

904

452

2

*

904

(378-209)-(209+378)

438

356

418

209

2

*

418

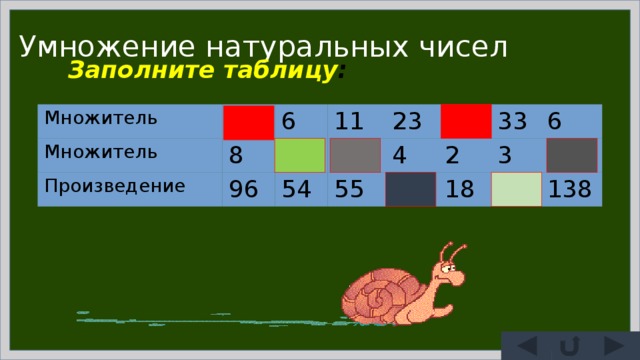
Умножение натуральных чисел

Заполните таблицу :

Множитель

12

Множитель

8

6

Произведение

9

96

11

5

54

23

4

9

55

2

33

52

6

3

18

23

99

138

Рациональный приём умножения чисел

на 11, 111 , 1111…

а) Умножение на 11 двузначных чисел, сумма разрядных единиц которых меньше 10.

б) Умножение на 11 двузначных чисел, сумма разрядных единиц которых равна или больше 10.

в) Умножение на 11 многозначных чисел

Занятие шестое

Объяснение рационального приёма умножения двузначных чисел на 11

• а) Чтобы умножить на 11 двузначное число, надо сложить количество единиц и десятков и полученный результат вставить между единицами и десятками:

Пусть надо 35*11.

Сложим 3+5=8; число 8 вставим между 3 и 5.

Значит, 35*11=385

• б) Если сумма разрядных единиц числа равна 10 – 18, надо количество единиц этого числа вставить между разрядными единицами, а 1 добавить к следующей разрядной единице.

• Пусть надо 49*11.

Сложим 4+9=13; число 3 вставим между 4 и 9, а 1 добавим к 4.

• Значит, 49*11=539

25

36

72

61

Тренировочные упражнения Цветик - семицветик

45

53

*11

81

57

77

64

Тренировочные упражнения Цветик - семицветик

39

48

95

*11

86

Умножение многозначных чисел на 11, 111…

• Пусть надо 352*11 .

1) Сложим 5+2=7; число 7 вставим между 5 и 2.

2) Сложим 3+5=8; число 8 вставим между 3 и 5.

• Значит, 352*11= 3872

• Пусть надо 35*111 .

Число единиц – 5.

Число десятков – 3+5= 8

Число сотен – 3+5= 8

• Значит:

35*111=3885

27*1111=29997

76*111=8436

Это полезно запомнить!

• 1*1= 1
• 11*11=1 2 1
• 111*111=12 3 21
• 1111*1111=123 4 321
• 11111*11111=1234 5 4321

• Запишите ответ:

• 111111*111111=
• 1111111*1111111=
• 11111111*11111111=
• 111111111*111111111=

Умножение чисел на 22, 33, 44 и т.д.

22 – это 2*11

33 – это 3*11

44 – это 4*11

Сделайте вывод самостоятельно

Занятие седьмое

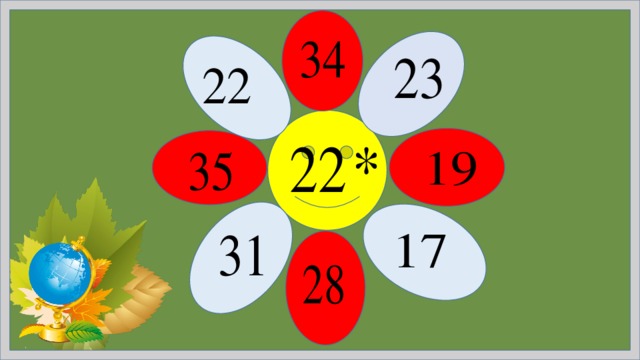
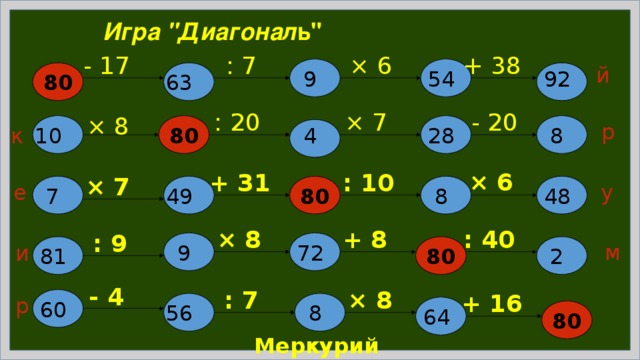
Игра "Диагонал ь"

- 17

× 6

+ 38

: 7

й

54

92

80

9

63

- 20

× 7

: 20

× 8

р

80

к

10

8

4

28

× 6

+ 31

: 10

× 7

е

80

у

48

49

7

8

+ 8

: 40

× 8

: 9

м

72

9

80

и

2

81

- 4

: 7

× 8

+ 16

р

60

8

56

64

80

Меркурий

Умножение двузначных чисел на 101, 1001, 10001…

Занятие восьмое

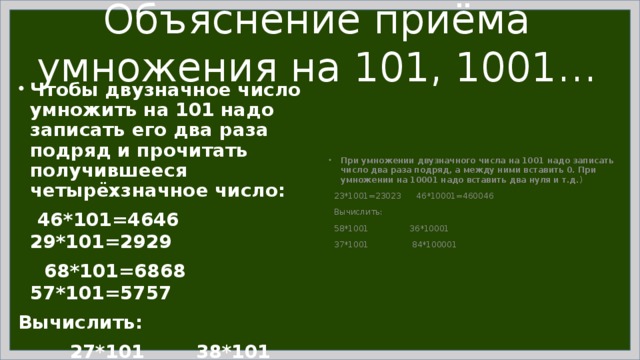
Объяснение приёма умножения на 101, 1001…

• Чтобы двузначное число умножить на 101 надо записать его два раза подряд и прочитать получившееся четырёхзначное число:

46*101=4646 29*101=2929

68*101=6868 57*101=5757

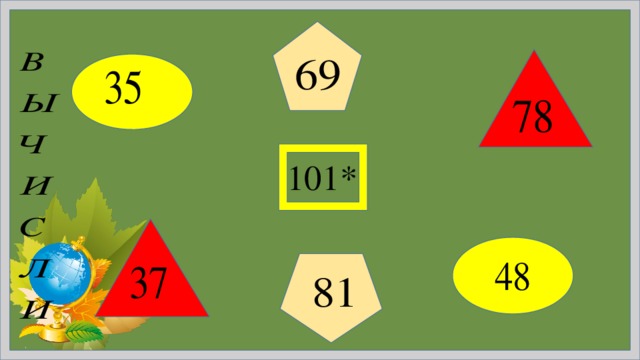
Вычислить:

27*101 38*101 25*101

76*101 95*101 87*101

• При умножении двузначного числа на 1001 надо записать число два раза подряд, а между ними вставить 0. При умножении на 10001 надо вставить два нуля и т.д. )

23*1001=23023 46*10001=460046

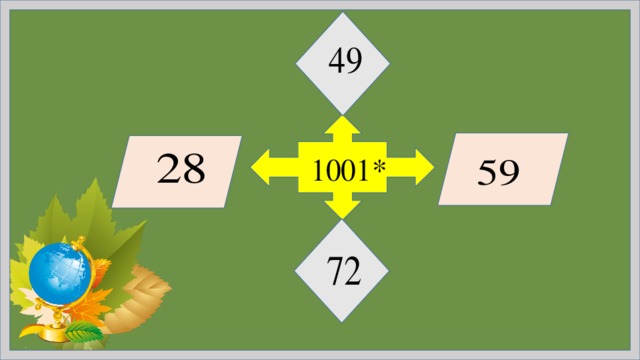
Вычислить:

58*1001 36*10001

37*1001 84*100001

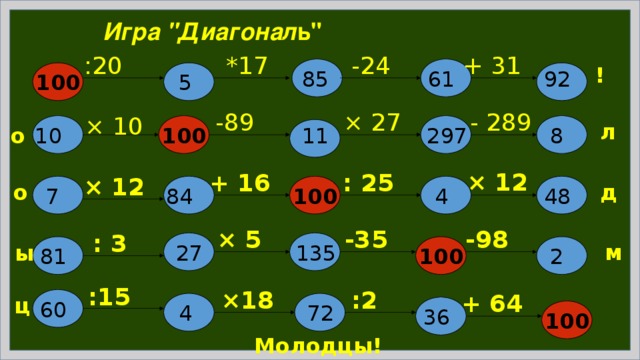
Игра "Диагонал ь"

:20

-24

+ 31

*17

!

61

92

100

85

5

- 289

× 27

-89

× 10

л

100

о

10

8

11

297

× 12

+ 16

: 25

× 12

о

100

д

48

84

7

4

-35

-98

× 5

: 3

м

135

27

100

ы

2

81

:15

×18

:2

+ 64

ц

60

72

4

36

100

Молодцы!

Ну-ка, в сторону карандаши!

Ни тетради, ни ручек, ни мела!

Устный счёт! Мы творим это дело только силой ума и души!

ИТОГОВОЕ ЗАНЯТИЕ I четверти

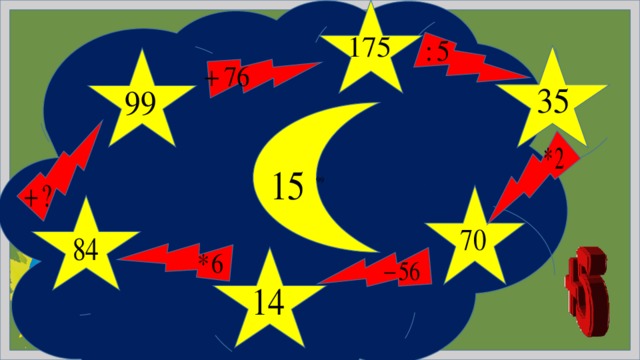
8

4

8

22

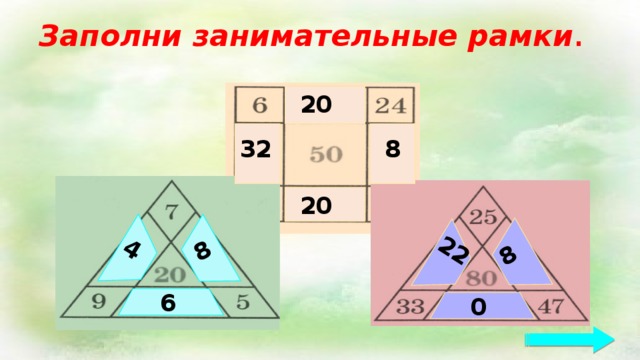
Заполни занимательные рамки .

20

8

32

20

6

0

Какой из результатов самый маленький?

11

1) (100 – 1) : 9 =

110

2) (1000 – 10) : 9 =

111

3) (1000 – 1) : 9 =

100

4) (1000 – 100) : 9 =

5) (100 – 10) : 9 =

10

19

27

84

56

72

92

38

Умножь на 25:

• Раздели число на 4.
• Если остаток 0 – припиши 2нуля.
• Если остаток 1 – припиши 25.
• Если остаток 2 – припиши 50.

Если остаток 3 – припиши 75.

48

Паша бросает дротики в мишень, изображённую справа. Сколько очков он не мог набрать за два броска?

60

80

100

90

120