Организация учебного процесса на уроках математики на основе компетентностно-контекстной модели обучения и воспитания

Малашко Е.И. – учитель математики ГБОУ СОШ пос.Октябрьский г.о.Похвистнево

Министерство образования и науки Самарской области

Государственное автономное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов

Самарский областной институт повышения квалификации и переподготовки работников образования

Итоговая работа

по модулю инвариантной части курсов повышения квалификации ИОЧ

«Основные направления региональной образовательной

политики в контексте модернизации российского образования»

по теме:

«Организация учебно-воспитательного процесса на уроках математики на основе компетентностно-контекстной модели обучения »

СРОКИ ОБУЧЕНИЯ: 1 сессия: с 28.10 по 01.11.2013 года

2 сессия: с 11.11 по 13.11. 2013 года

с 15.11. по 16.11.2013 года

Выполнила: Малашко Елена Ивановна, учитель математики

высшей квалификационной категории

ГБОУ СОШ пос.Октябрьский г.о.Похвистнево

Самара 2013

СОДЕРЖАНИЕ.

№п/п	Наименование раздела, пункта	Стр.
I	ВВЕДЕНИЕ
1.1.	Актуальность исследовательской работы	3-5
1.2.	Цель и задачи исследовательской работы.	5-6
1.3.	Ожидаемые результаты.	6-7
II	ОСНОВНАЯ ЧАСТЬ.
2.1.	Теоретическое описание модели.	7-10
2.1.2.	Описание изменений в образовательном процессе: Содержательно-технологический блок.	11-14
2.2.	Контрольно-оценочный блок .
2.2.1.	Методы исследования.	14-15
2.2.2.	Структура инструментария для оценки сформированности компетенции в компетентностно-контекстной модели обучения и воспитания.	15-17
2.2.2.1.	Диагностический инструментарий	17-18
2.3.	Ресурсный блок (условия)	19
III.	ЗАКЛЮЧЕНИЕ (выводы)	19-21
IV.	ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ	21-24
V.	ПРИЛОЖЕНИЯ.
5.1.	Приложение №1.Демоверсии проверочных работ по математике в 5 классе.	25-29
5.2.	Приложение №2.Проблемное обучение при достижении планируемых результатов на уроках математики.	29-35

I. ВВЕДЕНИЕ

В данной работе представлена система деятельности педагога на уроках математики на примере темы «Решение уравнений»

Целевая аудитория: обучающиеся 5 класса.

Соавторы в организации и осуществлении ИР- администрация школы.

Система деятельности выстраивается с детьми без разделения по половому признаку или в разновозрастных классах.

Работа над внедрением системы будет длиться в течение 3 лет (этап ИР –подготовительный)

1.1.Актуальность исследовательской работы.

Основная стратегическая цель образования в постиндустриальном обществе – переход от парадигмы преподавания (передачи информации) к парадигме учения (овладения компетенцией – потенциалом действия). Принятие и реализация в России новых стандартов общего образования призвано обеспечить достижение этой цели. Основным принципом, лежащим в основе организации процесса обучения и воспитания во всей системе непрерывного образования, является ориентация на результаты обучения, которые определены в рамках ФГОС нового поколения в виде компетенций как способностей целостного использования в деятельности освоенных знаний, умений, навыков, опыта и личностных качеств выпускника школы. Результаты общего образования определяются как единство предметного, метапредметного и личностного результатов при условии сохранения здоровья учащихся. Компетентностный подход рассматривается государством как один из главных путей достижения нового качества образования, как ключевая методология его модернизации, поэтому изучение вопросов проектирования и реализации компетентностностных моделей обучения в условиях внедрения ФГОС ООО имеет научную и практическую актуальность. Рассмотрим отличие по ряду показателей в традиционной модели обучения и в компетентностно-контекстной:

Показатели	Традиционная модель обучения	Компетентностно-контекстная модель обучения и воспитания
Обеспечивает развитие личности как..	субъекта отдельных действий (деятельности)	субъекта целостной деятельности
Освоение социального опыта происходит..	путем передачи учащемуся информации	в процессе организации учебно-познавательной деятельности контекстного типа, обеспечивающей триединство ее предметного, социального и рефлексивного компонентов
Освоение учеником принципов и способов построения целостной деятельности на компетентной основе осуществляется в результате	включение обучающегося в организацию учебно-познавательной деятельности разных отличных друг от друга (в зависимости от предмета) типа	включение обучающегося в организацию учебно-познавательной деятельности контекстного типа
Содержание усваиваемых школьниками научных знаний выстраивается	линейно, малыми дозами в логике его изложения в традиционном учебнике ЗУНы	упаковано в гипертексты – формы организации материала, при которых он предстает как многомерная сеть, как система конкретно указанных возможных переходов, связей между структурными единицами, составляя целостную, понятную учащимся ориентировочную основу деятельности, средство ее компетентного осуществления формирование предметных результатов образования
Цель использования проблемного обучения	Проблемные ситуации выступают как способ мотивация к получению знаний.	разрешение проблемной ситуации, в которой проблематизируются не знания, а способы их использования в контексте социального компонента учебной деятельности контекстного типа. Это обеспечивает формирование метапредметных результатов образования
		проблемные ситуации составляют единицу содержания обучения, а поступок выступает в качестве единицы деятельности обучающегося. Это обеспечивает формирование личностных результатов образования как ценностных ориентиров деятельности.

На данном этапе проведения исследовательской работы, в результате обобщения опыта ряда школ Самарской области была выявлено более высокая эффективность организации учебно-воспитательного процесса в образовательных областях русский язык и математика на основе компетентностно-контекстной модели по сравнению с традиционной по уровню сформированности компетентности учащихся. Однако широкое внедрение компетентностно-контекстной модели обучения и воспитания в практику работы образовательных учреждений ограничено в силу неразработанности дидактического обеспечения организации учебно-воспитательного процесса на основе компетентностно-контекстной модели: отсутствуют обстоятельные методические разработки и рекомендации по организации деятельности учителя и обучающихся на различных этапах организации компетентностно-контекстной модели. Требуется адаптация основных положений организации образовательного процесса на основе компетентностно-контекстной модели к конкретным учебным предметам.

1.2.Цель и задачи исследовательской работы.

Потребность найти способы дидактического обеспечения организации учебно-воспитательного процесса на уроках математики на основе компетентностно-контекстной модели обучения и воспитания определяют актуальность исследования и его проблему - определение системы дидактических средств, обеспечивающих реализацию компетентностно-контекстной модели обучения и воспитания в общеобразовательной школе на уроке математики.

Объект исследования – контекстно-компетентностная модель организации процесса обучения на уроке математики в общеобразовательной школе.

Предмет исследования – дидактические характеристики компетентностно-контекстной модели обучения, средства и способы ее реализации на уроке математики.

Цель исследования - разработка системы дидактического обеспечения организации учебно-воспитательного процесса в общеобразовательной школе на основе компетентностно-контекстной модели обучения и воспитания на уроке математики.

Задачи исследования:

• выявить и обосновать систему дидактического обеспечения организации учебно-воспитательного процесса на уроке математики в общеобразовательной школе на основе компетентностно-контекстной модели обучения и воспитания;

• спроектировать и описать модельные характеристики деятельности учителя и обучающихся на уроке, методов обучения как способов взаимодействия субъектов процесса обучения в компетентностно-контекстной модели обучения и воспитания;

• спроектировать и описать требования к организации содержания обучения в компетентностно-контекстной модели обучения и воспитания;

• экспериментально проверить эффективность разработанной системы дидактического обеспечения организации учебно-воспитательного процесса в общеобразовательной школе на основе компетентностно-контекстной модели обучения и воспитания;

• на основе результатов теоретического и эмпирического исследования разработать методические рекомендации для педагогов по организации учебно-воспитательного процесса в общеобразовательной школе на основе компетентностно-контекстной модели обучения и воспитания.

1.3.Ожидаемые результаты.

• Теоретическая значимость исследования.

Результаты исследовательской работы позволят осуществить выход за рамки традиционной одномерной модели обучения, расширят научные представления о способах дидактического обеспечения учебно-воспитательного процесса на уроке математики в общеобразовательной школе на основе компетентностно-контекстной модели обучения и воспитания. Обоснование сущности, содержания и методов обучения составит основу для научных представлений о реальных механизмах организации учебно-воспитательного процесса в общеобразовательной школе адекватного идеям компетентностного подхода и стандартов второго поколения.

• Практическая значимость исследования.

Результаты будут способствовать совершенствованию педагогической деятельности в аспекте организации процесса обучения и воспитания на уроке математики в общеобразовательной школе на основе компетентностно-контекстной модели. Разработка и апробация методических рекомендаций по организации учебно-воспитательного процесса на уроках математики на основе компетентностно-контекстной модели обучения и воспитания может стать реальной предпосылкой повышения качества образования и компетентности педагога в области организации инновационного процесса обучения адекватного идеям компетентностного подхода как конструктивного отрицания традиционной модели обучения.

II. ОСНОВНАЯ ЧАСТЬ.

2.1. Теоретическое описание модели.

В рамках опытно-экспериментальной работы СИПКРО по проблеме «Проектирование компетентностно-ориентированной образовательной среды», наша школа являлась экспериментальной площадкой института для апробации и внедрения новых педагогических технологий с 1 сентября 2008 года по 1 сентября 2012 года. В результате эксперимента было сформулировано определение компетенции как качества личности, представляющего собой интегральную совокупность, по сути, систему когнитивного, социального и рефлексивного опыта, обеспечивающую способность человека к сознательному преобразованию действительности на основе умения устанавливать связь между знаниями и ситуациями его практического действия и поступка.

Когнитивный опыт обеспечивает усвоение, хранение, упорядочение и использование наличной и поступающей информации, способствует воспроизведению в психике познающего субъекта устойчивых закономерностей окружающей действительности.

Социальный опыт обеспечивает продуктивность совместной деятельности и общения, способность понимать себя и других в условиях динамики психических состояний, межличностных отношений и условий социальной среды.

Рефлексивный опыт обеспечивает способность быть субъектом деятельности и успешно управлять ею «на основе анализа и осознания уже выполненных ранее деятельностей и полученных в них продуктов» (Г.П.Щедровицкий).

Формирование компетенции как интегральной совокупности трех указанных видов опыта, определяющей новый результативно-целевой ориентир развития общего среднего образования невозможно обеспечить в рамках традиционных моделей, методологически и технологически обеспечивающих усвоение в основном предметных знаний. Основой проектирования модели обучения, обеспечивающей формирование компетенции, на научно-теоретическом и конструктивно-технологическом уровнях может стать теория контекстного обучения (образования), разрабатываемая в научно-педагогической школе А.А. Вербицкого.

На научно-теоретическом уровне теория контекстного подхода как методологический инструмент педагогического исследования позволила в процессе опытно-экспериментальной работы спроектировать модель учебно-познавательной деятельности школьника, обеспечивающую формирование компетенции как интегральной совокупности трех видов опыта через рассмотрение их «внутри контекста, в котором они происходят» (А.А. Вербицкий). Так как опыт есть результат деятельности, то приобрести его можно только в контексте той деятельности, результатом которой он является. Виды деятельности, в контексте которых формируются соответствующие виды опыта, в свою очередь, можно рассматривать в качестве структурных компонентов моделирования нового вида учебно-познавательной деятельности школьников, адекватной идеям компетентностного подхода (рис.1). Когнитивный опыт формируется в процессе предметной деятельности и предполагает структурную организацию знаний, позволяющую учащимся оперировать признаками объекта, правилами их комбинации, сравнения, интерпретации.

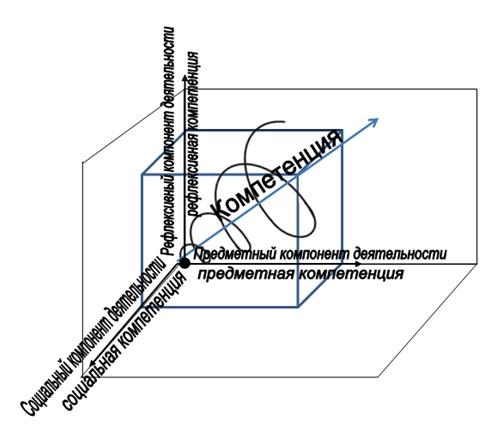
Рис. 1. Трехмерная модель учебно-познавательной деятельности контекстного типа

Когнитивный опыт позволяет человеку понять значение изучаемого явления. Процесс осмысления значений осуществляется в контексте социального компонента познавательной деятельности, где когнитивный опыт используется для решения различных учебных и практико-ориентированных задач и проблем. Предметом этого компонента деятельности обучающегося выступает не содержание обучения, а способы организации продуктивной совместной деятельности и общения, составляющие содержание социального опыта.

Рефлексивный опыт формируется в процессе реализации рефлексивного компонента деятельности обучающегося, позволяющей ему осуществлять

переход «от одного объекта деятельности индивида, принимающего сообщение к другому объекту – самой деятельности индивида – объекту, объемлющему первый» (Г.П. Щедровицкий). Возможность осуществления данного перехода обеспечивается наличием когнитивного и социального видов опыта.

Предметный, социальный и рефлексивный компоненты учебно-познавательной деятельности составляют образовательное пространство контекстного типа, выводящее деятельность школьников за рамки предметной одномерности.

Трехмерная модель учебно-познавательной деятельности школьников контекстного типа обеспечивает развитие личности как субъекта целостной деятельности. Кольцевая структура деятельности, модель которой разработана в рамках теории контекстного обучения А.А.Вербицким, не изменяется, а с изменением и усложнением предмета деятельности происходят соответствующие изменения во всех ее компонентах (мотивах, поступках, средствах и т.д.), то есть развитие субъекта деятельности осуществляется по спирали.

2.1.2.Описание изменений в образовательном процессе:

Содержательно-технологический блок.

В процессе проводимой экспериментальной работы была спроектирована и апробирована компетентностно-контекстная модель образовательного процесса на уроке, характерными особенностями которой являются следующие позиции :

1. Освоение социального опыта осуществляется не просто путем передачи учащемуся информации, а в процессе организации учебно-познавательной деятельности контекстного типа, обеспечивающей триединство ее предметного, социального и рефлексивного компонентов.

2. Включение обучающегося в организацию учебно-познавательной деятельности контекстного типа, обеспечивает в рамках общего образования освоение им принципов и способов построения целостной деятельности на компетентной основе.

3. Содержание усваиваемых школьниками научных знаний выстраивается не линейно, малыми дозами в логике его изложения в традиционном учебнике, а упаковано в гипертексты – формы организации материала, при которых он предстает как многомерная сеть, как система конкретно указанных возможных переходов, связей между структурными единицами, составляя целостную, понятную учащимся ориентировочную основу деятельности, средство ее компетентного осуществления. Это обеспечивает формирование предметных результатов образования.

4. В качестве основного механизма, позволяющего обучающемуся освоить способы компетентного действия на основе знания, выступает разрешение проблемной ситуации, в которой проблематизируются не знания, а способы их использования в контексте социального компонента учебной деятельности контекстного типа. Это обеспечивает формирование метапредметных результатов образования.

5. В компетентностно-контекстной модели обучения проблемные ситуации составляют единицу содержания обучения, а поступок выступает в качестве единицы деятельности обучающегося. Это обеспечивает формирование личностных результатов образования как ценностных ориентиров деятельности.

Проведенный эксперимент подтвердил более высокую эффективность организации учебно-воспитательного процесса на основе компетентностно-контекстной модели по сравнению с традиционной по уровню сформированности компетентности учащихся в образовательной области математика.

В компетентностно-контекстной модели процесс обучения изучение любой темы математики происходит в 4 этапа:

1 этап – осознание структуры изучаемого явления, задачей которого является формирование у учащихся когнитивной схемы изучаемого явления. Для этого, как было показано выше, изучаемый материал сжимается и представляет собой не столько содержательную, сколько функциональную сущность изучаемого явления, позволяющую использовать его как инструмент решения большого класса задач. Сформированная когнитивная схема выступает в качестве основы формирования предметных, метапредметных и личностных результатов образования.

2 этап - осознание генезиса способов деятельности, где и формируются познавательные универсальные учебные действия, связанные с содержание учебного материала, такие как моделирование, структурирование, анализ, сравнение, классификация, оценка, и т.д. Для этого учитель представляет учащимся ряд задач, выстроенных по принципу «от простого к сложному» и организует деятельность учащихся «во внешней речи»: объяснение способа решения задачи на основе когнитивной схемы.

3 этап – самореализация. На данном этапе формируются универсальные учебные действия, не связанные с содержание образования: регулятивные, коммуникативные, познавательные (постановка и решение проблем). Для этого учитель организует коллективную деятельность, в процессе которой учащиеся определяют уровень достижений, темп и объем работы и работают по индивидуальным траекториям.

4 этап – рефлексия уровня достижений. На данном этапе осуществляется формирование рефлексивного мышления. Элементы рефлексии (контроля) осуществляются на протяжении всего времени изучения темы в виде небольших тестов, самостоятельных работ. В частности обязательными являются проверочные работы в завершении этапа осознания генезиса способов деятельности, в процессе этапа самореализации. Если изучается достаточно объемный теоретический материал, то, как правило, в завершении этапа осознания структуры изучаемого явления проводится устный опрос.

Формирование регулятивных, коммуникативных и личностных универсальных учебных действий заложено в самой компетентностно-контекстной модели процесса обучения и отрабатывается в процессе изучения каждой темы на третьем и четвертом этапах. Предметные результаты и познавательные универсальные учебные действия, которые непосредственно связаны с содержанием образования, конкретизируются в каждой изучаемой теме по каждому предмету в учебно-тематическом плане учителя. Для этого в учебно-тематическом плане по каждой теме учителем формулируются результаты обучения в деятельной форме, то есть определяется, что будет уметь делать учащийся с помощью нового знания и конкретизируются познавательные универсальные учебные действия. На основании заявленных результатов учитель строит сценарий изучения темы в четыре выше указанных этапа, время на прохождение каждого их которых примерно распределяется следующим образом: 1 этап – 20%, 2 этап – 10%, 3 этап – 40%, 4 этап – 30% (указан % времени на каждый этап от общего количества времени, отведенного на изучение темы).

Каждому этапу изучения темы соответствует определенная форма организации учебных занятий:

1 этап – проблемное изложение материала;

2 этап – семинар, в процессе которого организована деятельность по объяснению выбора основ решения широкого класса задач (генезис способов деятельности);

3 этап – практикум по решению задач, в процессе которого каждый учащийся в коллективной деятельности строит свою работу по достижению личностно-значимых целей обучения (на этом же этапе могут проводиться лабораторные и практические работы, если это предусмотрено учебным планом);

4 этап – двухфазная рефлексия, состоящая, как правило, из трех уроков: предытоговая работа, рефлексия уровня достижений (обобщаюший урок), итоговая работа. Особенность этапа заключается в том, что две проверочные работы данного этапа проводятся по одному классификатору. Эти же работы задают уровень сложности освоения материала. В рамках заявленной темы он может быть различным в зависимости от уровня подготовки учащихся, но не может быть ниже уровня «учащийся научиться», заданного примерной образовательной программой основного общего образования. На этом же этапе проводятся уроки защиты проекта, если это предусмотрено учебным планом.

Особенности изучения темы «Решение уравнений в 5 классе» в данной модели представлен в Приложении №2.

2.2. Контрольно-оценочный блок

2.2.1.Методы исследования.

Для решения поставленных задач и проверки исходных предположений будет использован комплекс взаимодополняющих методов исследования, адекватных его предмету: анализ педагогической, психологической литературы; психологические методы (анкетирование, опросники); педагогические (оценка результатов учебной деятельности); наблюдение (прямое, косвенное, включенное); экспериментальные методы (формирующий эксперимент); изучение и обобщение педагогической деятельности; математико-статистические методы (средние значения, ассоциативный анализ).

2.2.2. Структура инструментария для оценки сформированности компетенции в компетентностно-контекстной модели обучения и воспитания.

В последнее время активно разрабатывается концепция гуманитарной экспертизы образования (С.Л.Братченко). Основные ее идеи и конкретная модель такого типа экспертизы (М.И.Лукьянова) были нами использованы как теоретические основы оценки сформированности компетенции в компетентностно-контекстной модели обучения и воспитания.

При разработке инструментария мы исходили из того, что не существует прямых способов измерения уровня сформированности компетенции. Поэтому для измерения уровня ее сформированности были использованы методики измерения уровня сформированности составляющих компетенции как качества личности, представляющего собой интегральную совокупность, по сути, систему когнитивного, социального и рефлексивного опыта, обеспечивающую способность человека к сознательному преобразованию действительности на основе умения устанавливать связь между знаниями и ситуациями его практического действия и поступка (рис. 1).

КОМПЕТЕНЦИЯ

КОГНИТИВНЫЙ ОПЫТ

СОЦИАЛЬНЫЙ ОПЫТ

РЕФЛЕКСИВНЫЙ ОПЫТ

Рис. 1. Трехкомпонентная модель компетенции

Когнитивный опыт обеспечивает усвоение, хранение, упорядочение и использование наличной и поступающей информации, способствует воспроизведению в психике познающего субъекта устойчивых закономерностей окружающей действительности. Социальный опыт обеспечивает продуктивность совместной деятельности и общения, способность понимать себя и других в условиях динамики психических состояний, межличностных отношений и условий социальной среды. Рефлексивный опыт обеспечивает способность быть субъектом деятельности и успешно управлять ею «на основе анализа и осознания уже выполненных ранее деятельностей и полученных в них продуктов» (Г.П.Щедровицкий).

В соответствии с представленной трехкомпонентной моделью компетенции нами была определена структура инструментария оценки уровня сформированности компетенции в компетеностно-контекстной модели обучения, позволяющая изучить качественные и количественные изменения, происходящие:

- в когнитивном опыте (предметная компетенция);

- в социальном опыте (социальная компетенция);

- в рефлексивном опыте (рефлексивная компетенция).

В качестве критерия сформированности компетенции в компетентностно-контекстной модели обучения и воспитания рассматривается высокий уровень сформированности всех трех аспектов, выступающих в качестве основных диагностируемых показателей. Диагностический маршрут оценки сформированности компетенции и используемый диагностический инструментарий представлены на схеме 1.

Диагностический маршрут оценки сформированности компетенции в компетентностно-контекстной модели обучения и воспитания

КОМПЕТЕНЦИЯ

Диагностические параметры

Диагностический инструментарий

Социальная компетенция

Рефлексивная компетенция

Когнитивная компетенция

Контрольные работы по предметам школьного курса

Методика Л.М.Фридмана «Что нам интересно?», опросник для измерения потребности в достижениях Ю.М.Орлова

Высокий уровень и положительная динамика результатов двух предыдущих исследований

2.2.2.1.Диагностический инструментарий:

• предметная компетенция

Уровень сформированности предметной компетенции выявляется на содержательном материале математики. Для этого нужна педагогическая диагностика посредством самостоятельных работ учащихся, выявляющая уровень владения фактическим материалом математики (от стандартного до повышенного уровня сложности, требующего комбинации различных способов действий). Другими словами, работы учащихся, отражающие те параметры, которые составляют сущность когнитивного опыта учащихся. Образец проверочных работ представлен в Приложение №1. Очень важно, что учитель разрабатывает демоверсии проверочных работ, текст которых находится в свободном доступе для учащихся (сайт школы и стенд в кабинете).

• социальная компетенция

Уровень сформированности социальной компетенции выявляется на основе двух исследований: изучения уровня сформированности познавательных интересов и мотивов и мотивации достижения, составляющих сущность социального опыта учащихся.

Выявление характера учебной мотивации и познавательных интересов учащихся с помощью Методики Л.М.Фридмана «Что нам интересно?», позволяет объяснить направленность действий учащихся, организованность и устойчивость целостной деятельности как социального навыка.

Потребность в достижениях (опросник Ю.М.Орлова. Учащиеся 5-11 классов.) выступает источником активности личности. Она определяется уровнем самооценки человека. При адекватной самооценке, чем выше уровень потребности в достижениях, тем активнее и целенаправленнее человек.

• рефлексивная компетенция

Уровень сформированности рефлексивной компетенции выявляется на основе высокого уровня и положительной динамики результатов двух предыдущих исследований. Это объясняется тем, что основой рефлексивного опыта выступает индивидуальная способность человека устанавливать границы собственных возможностей, знать, что он знает и чего не знает. Что и позволяют выяснить исследования предметной компетенции и изучения познавательных мотивов и интересов. Основной формой отношений в рамках рефлексивного опыта выступает отношение учащегося с самим собой: «Я неумелый, незнающий – Я умелый, знающий». Учебно-воспитательный процесс, приводящий к построению таких отношений, обеспечивает самоопределение и самоизменение учащегося, способность к которым фиксируются методикой изучения потребности в достижениях.

2.3. Ресурсный блок (условия)

1. Методическое обеспечение. Организация учебного процесса на уроках математики на основе компетентностно-контекстной модели обучения и воспитания выполнима лишь при условии безусловного следования 4 этапам организации учебного процесса (п.2.2.1.).

2. Кадровые условия. Повышение квалификации педагогов через участие в системе постоянно действующих практико-ориентированных семинаров (посещение и демонстрация уроков и мастер-классов на уровне всех школ, участвующих в эксперименте), что позволит им разработать систему дидактического обеспечения организации учебно-воспитательного процесса в общеобразовательной школе на основе компетентностно-контекстной модели обучения и воспитания на уроке математики.

3. Информационные и материально-технические условия. В ОУ должна быть организована возможность свободного доступа школьников и педагога к информационным сервисам, позволяющим пользоваться ресурсами сети Интернет для реализации индивидуальных и групповых образовательных проектов. В ОУ необходим дидактический материал последнего поколения с заданиями уровня А, В, С в количестве достаточном для каждого ученика.

4. Финансово-экономические условия реализации программы. В ОУ необходимо разработать и применять систему поощрения педагогов, участвующих в эксперименте.

III. ЗАКЛЮЧЕНИЕ (выводы)

Модель компетентностно-контекстногопроцесса обученияи воспитания предполагает включение учащихся в учебную деятельность контекстного типа, интегрирующую предметную, социальную и рефлексивную виды деятельности, совокупность которых обеспечивает формирование и развитие у обучающихся навыков осуществления целостной деятельности.

Мы исходим из того, что успешная реализация и распространение данной модели обучения и воспитания на уроках математики возможна, если она будет обеспечена дидактическими средствами, позволяющими учителю без больших затруднений и энергетических затрат воспроизводить компетентностно-контекстную модель обучения и воспитания в процессе изучения математики. Это становится реальностью, если для компетентностно-контекстной модели обучения:

- разработана модельная характеристика деятельности учителя, позволяющая ему изменить стиль преподавания (от монологического изложения учебного материала, доминирования на каждом этапе урока - к диалогу учителя и обучающихся, к системе тьюторского сопровождения самореализации обучающегося);

- разработана модельная характеристика деятельности обучающихся на различных этапах обучения, обеспечивающая им переход от репродуктивной, «ответной» позиции, пассивного приема и запоминания учебной информации – к созиданию образа мира в себе самом посредством активного полагания себя в мир предметной, социальной и рефлексивной деятельности;

- разработана характеристика методов обучения, как способов взаимодействия учителя и обучающихся на различных этапах обучения, задающих вектор изменения организации процесса обучения от традиционных «сообщающих» методов – к инновационным педагогическим технологиям, реализующим принципы совместной деятельности и творческого взаимодействия педагога и обучающихся, единства познавательной, социальной и рефлексивной деятельности;

- определены требования к гипертекстовой форме организации учебной информации, как системной ориентировочной основе компетентных практических действий и поступков, служащей механизмом запуска копетентностно-контекстной модели обучения и воспитания;

- определены требования к системе учебных задач и проблемных ситуаций на каждом этапе обучения, обеспечивающей самореализацию учащихся в учебной деятельности контекстного типа. Построение изучаемого материала в данной модели предполагает наращивание (приращивание) знаний к уже имеющимся, а не изучение всего заново, только в большем объёме.

Эффекты. Будут готовы образцы методических разработок организации процесса обучения и воспитания на уроках математики на основе компетентностно-контекстной модели.

Риски. Обобщение результатов теоретического и эмпирического исследования производиться научным руководителем в научно-педагогической школе А.А. Вербицкого. В случае потери связи с научным консультантом и руководителем (форс-мажорные обстоятельства) школа будет иметь лишь собственный опыт и не сможет объективно представить методические рекомендации для педагогов других школ по организации учебно-воспитательного процесса на основе компетентностно-контекстной модели обучения и воспитания.

IV. Информационные источники:

Основные источники

1. Асмолов А. Г. Психология личности: культурно-историческое понимание развития человека. – М., 2007.

2. Баева И.А. Психологическая безопасность в образовании. Спб.: Издательство «Союз», 2002, 271 с.

3. Баева И.А. И др. Психология безопасности как теоретическая основа гуманитарных технологий в социальном взаимодействии / Под ред. И.А. Баевой. СПБ.: Изд-во РГПУ им. А.И. Герцена. 2007. 289 с.

4. Болотова Е. Нормативно-правовая база современного урока // Народное образование. – 2009. – № 9. – С. 118.

5. Жильцова О. А. Организация исследовательской и проектной деятельности школьников // Дистанционная поддержка педагогических инноваций при подготовке школьников к деятельности в сфере науки и высоких технологий. – М., 2007.

6. Касицина Н.В., Михайлова Н.Н., Юсфин С.М. Четыре тактики педагогики поддержки. Эффективные способы взаимодействия учителя и ученика. Спб.: Агенство образовательного сотрудничества. Образовательные проекты. Речь. М.: Сфера, 2010, 188с.

7. Рыбакина Н.А. и др. Проектирование компетентностно-ориентированной образовательной среды.-Самара: ГОУ СИПКРО, 2010-259с.

Нормативные документы

1. Закон РФ об образовании

2. Конституция Российской Федерации. М., 1996. - 80 с.

3. Концепция федеральных государственных образовательных стандартов общего образования: проект / Рос. акад. образования; под ред. А. М. Кондакова, А. А. Кузнецова. – М.: Просвещение, 2008.

4. Национальная образовательная инициатива «Наша новая школа»: утв. Президентом Российской Федерации 4 февраля 2010 г. № Пр-271.

5. План действий по модернизации общего образования на 2011-2015 годы : утв. распоряжением Правительства Российской Федерации от 7 сентября 2010 г. № 1507-р.

6. План действий по модернизации общего образования, направленных на реализацию национальной образовательной инициативы «Наша новая школа» на период 2011-2015 годов (утвержден постановлением Правительства Самарской области от 21.10.2010 года № 507)

7. ФГОС основного общего образования утвержден приказом от 17 декабря 2010 года №1897 (зарегистрирован Минюстом России 01.02.2011 г. №19644)

8. Федеральная целевая программа развития образования на 2011-2015 годы : утв. постановлением Правительства Российской Федерации от 7 февраля 2011 г.

9. Федеральные требования к образовательным учреждениям в части минимальной оснащенности учебного процесса и оборудования учебных помещений: утв. приказом Минобрнауки России от 4 октября 2010 г. № 986.

10. Федеральные требования к образовательным учреждениям в части охраны здоровья обучающихся (приказ Минобрнауки России от 28.12. 2010г. № 2106)

Интернет ресурсы:

1. http://www.mon.gov.ru – cайт Министерства образования и науки РФ

2. http://samregion.edu.ru - cайт Министерства образования и науки Самарской области

Дополнительные источники

1. Болотов В., Г. Ковалева Опыт России в области оценки образовательных достижений школьников. Каковы современные пути и способы совершенствования управления качеством образования? // Инновационные проекты и программы в образовании. – 2010. – №5. – С.3-10.

2. Выбор в современной школе: книга для учителя. СПб.: «Водолей», 2002

3. Граничина О.А. Статистические методы психолого-педагогических исследований (Учебное пособие) - Санкт- Петербург: Издательство РГПУ им.А.И.Герцена, 2002.

4. Дронов В. П., Кондаков А. М. Новый стандарт общего образования – идеологический фундамент российской школы // Педагогика. – 2009. – № 4. – С. 22-Компетентностный подход в педагогическом образовании: Коллективная монография/ под ред. проф. В.А.Козырева и проф. Н.Ф. Родионовой. СПб.: РГПУ. 2004.

5. Образовательные технологии: достижение прогнозируемых результатов. – М. : Про-Пресс, 2009. – 56 с. – (Библиотечка журнала «Вестник образования России»).

6. Чернобай Е. В. Методика конструирования урока с использованием электронных образовательных ресурсов // Стандарты и мониторинг в образовании. – 2010. – № 1. – С . 11-14

7. Шмелькова Л. В. Требования к образовательным учреждениям в части охраны здоровья обучающихся вопросах и ответах // Администратор образования. – 2011. – № 10. – С. 79-82.

8. Хуторской А. В. Технология проектирования ключевых и предметных компетенций.- М.,2005.

V. ПРИЛОЖЕНИЯ.

Приложение №1.

ДЕМОверсии проверочных работ по математике

5 класс. Диагностическая работа №1.

«Натуральные числа. Арифметические действия с натуральными числами.»

№ задания	Элементы содержания	Формируемые умения	Уровень сложности	Максим. балл за выполнение
1	Десятичная система счисления. Запись и чтение многозначных чисел.	Читать и записывать многозначные числа. Владеть понятиями «класс», «разряд», «разрядное слагаемое».	Б	1
2	Буквенные выражения. Значения буквенного выражения.	Составлять буквенные выражения. Находить значение буквенного выражения при определенных значениях входящих в него букв	Б	1
3	Применение свойств арифметических действий при нахождении значения числового выражения	Знать и применять свойства арифметических действий при нахождении значения числового выражения	Б	1
4	Упрощение буквенных выражений	Упрощать буквенные выражения и выполнять числовые подстановки	Б	1
5	Решение текстовых задач арифметическими приёмами	Составлять математическую модель текстовой задачи. Осуществлять переход от словесной формулировки соотношений между величинами к алгебраической	П	2
6	Решение уравнений	Знать и находить компоненты арифметических действий	а,б – Б В -П	1 2
7	Решение текстовых задач алгебраическим способом	Закрепить решение задач на «уравнение»	П	2

Вариант работы

1. Какая цифра стоит в разряде сотен миллиардов числа 382 754 200 000?

2. Купили a кг конфет по цене 75 рублей за килограмм и 2 кг печенья по цене 104 рубля за килограмм. Сколько рублей стоит вся покупка?

3. Выражение 2•17•5•3 Саша упростил так: 2•17•5•3=(17•3)•(2•5)=510. Какие свойства арифметических действий применил Саша?

4. Найдите значение выражения 232a•25+200 при a=1.

5. За пять журналов и три газеты заплатили 616 рублей, а за 2 журнала и три газеты заплатили 277 рублей. Сколько рублей стоит один журнал и одна газета?

6. Решите уравнения

А)(у-263) -97 = 538 б) (9 + 7х) •6=288 в)(17х-8х+3) :7 =12

7. Реши задачу с помощью уравнения:

Три фермера закупили для посева 1957 кг ячменя. Второму фермеру нужно в 5 раз меньше ячменя, чем первому , а третьему- в 3 раза меньше, чем второму. Сколько кг ячменя нужно каждому фермеру?

5 класс. Диагностическая работа №2.

«Десятичные дроби. Арифметические действия с десятичными дробями.»

№ задания	Элементы содержания	Формируемые умения	Уровень сложности	Максим балл за выполнение
1	Понятие десятичной дроби. Записи и чтение десятичных дробей	Формировать представление о десятичной дроби. Читать и записывать десятичные дроби	Б	1
2	Сравнение десятичных дробей	Понимать отношение «больше», «меньше», «равно».	Б	1
3	Приближенное значение чисел. Округление чисел	Знать и применять правила округления чисел	Б	1
4	Сложение и вычитание десятичных дробей	Владеть алгоритмами письменного сложения и вычитания десятичных дробей. Применять свойства арифметических действий при упрощении выражений	Б	1
5	Умножение и деление десятичных дробей	Владеть алгоритмами письменного умножения и деления десятичных дробей	Б	1
6	Среднее арифметическое нескольких чисел	Находить среднее арифметическое нескольких чисел	Б	1
7	Решение уравнений	Знать и находить компоненты арифметических действий	Б	1
8	Решение текстовой задачи арифметическим способом	Составлять математическую модель текстовой задачи. Решать задачу арифметическим способом	П	2

Вариант

1. Запишите число 17,0201 в виде обыкновенной дроби.

2. Вставьте пропущенную цифру, чтобы выполнилось неравенство 3,1

3. Округлите число 28,475 до разряда десятых долей.

4. Найдите сумму числа 2,57 и разности 18,23-7,3.

5. Упростите выражение 7,35x-5,8x-5,8:y.Найдите его значение при x=3,6,y=10.

6. Запишите выражение для вычисления среднего арифметического трех чисел, еслиформировать представление о десятичной дроби. Читать и записывать десятичные дроби первое число у и она в 4,5 раза меньше второго и в 2 раза больше третьего числа.

7. Решите уравнение 8,3а+2а-60,5=320,6.

8. Моторная лодка проплыла против течения реки 15,6 км за 1,3 часа, а по течению 37,4 км за 2,2 часа. За сколько часов плот проплывет 7,5 км по этой реке?

5 класс. Диагностическая работа №3. Текстовые задачи.

№ задания	Элементы содержания	Формируемые умения	Уровень сложности	Максим балл за выполнение
1	Задачи на разностное и кратное сравнение	Применять смысл отношений «больше (меньше) на (в) …» при решении задач	Б	1
2	Задачи на части	Закрепить решение задач на части	Б	1
3	Решение задач на «уравнивание»	Закрепить решение задач на «уравнивание»	Б	1
4	Задачи на движение	Понимать взаимосвязь величин: скорость, время, расстояние. Уметь находить скорость «удаление», скорость «сближения»	Б	1
5	Задачи на движение по реке	Различать скорости движения: собственную, по течению, против течения	Б	1
6	Задачи на совместную работу	Отработать общие подходы при решении задач на совместную работу	Б	1
7	Комбинаторные задачи	Познакомить с комбинаторными задачами со способами из решения	Б	1
8	Работа с текстовыми задачами	Интегрировать знания при решении задач	П	2

Вариант

1. Саша прыгнул в длину на 286 см. Это на t см меньше, чем Вова. Длина прыжка Васи в 2 короче прыжка Вовы. Составьте выражение для нахождения длины прыжка Васи.

2. Брат с сестрой собрали вместе 54 ореха. Брат собрал в 2 раза больше орехов, чем сестра. Сколько орехов собрал брат?

3. В двух пачках 63 тетради, причем в первой пачке на 7 тетрадей больше, чем второй. Сколько тетрадей в каждой пачке?

4. Два мотоциклиста движутся на встречу друг к другу. Скорость первого мотоциклиста 80 км/ч, второго – 90 км/ч. Через, сколько часов они встретятся, если сейчас между ними 340 км?

5. Катер плывет от одной пристани до другой против течения реки 4 часа. Собственная скорость катера 14 км/ч, скорость течения реки 2 км/ ч. За какое время катер проплывет обратный путь?

6. Ткацкой фабрике надо наткать 800 м ситца. Первая бригада может выполнить всю работу за 8 дней, а вторая – за 16 дней. За сколько дней выполнят эту работу бригады, если будут работать вместе?

7. Иван Петрович забыл код замка при входе в подъезд. Но он помнил, что код состоит из двух цифр: или 3,или 4, или 5, причем цифры не повторялись. Найдите наибольшее число возможных кодов, которые надо перебрать Ивану Петровичу, чтобы войти в подъезд.

8. В автобусе ехали 132 пассажира. На первой остановке вышли 27 пассажиров и вошли 15 человек. На второй остановки вышла 1/6 часть пассажиров, ехавших в автобусе, а вошли 10 человек. Сколько пассажиров ехало в автобусе после второй остановки

Итоговый тест за курс математики 5 класса

№ задания	Элементы содержания	Формируемые умения	Уровень сложности	Максим балл за выполнение
1	Натуральные числа	Выполнение арифметических действий с натуральными числами: вычисление квадрата и куба числа	Б	1
2	Элементы алгебры	Составление буквенного выражения по условию задачи: нахождение числового значения буквенного выражения	Б	1
3	Дроби	Нахождение части целого и целого по части	Б	1
4	Дроби	Преобразование обыкновенных дробей: сравнение и упорядочивание обыкновенных дробей	Б	1
5	Элементы алгебры	Решение уравнений; нахождение неизвестных компонентов арифметических действий	Б	1
6	Дроби	Решение простейших задач на процентов	Б	1
7	Измерения, приближения, оценки. Зависимость между величинами	Выражение одних величин через другие; округление натуральных чисел	Б	1
8	Работа с текстовыми задачами	Решение текстовых задач арифметическим способом	Б	1
9	Наглядная геометрия	Нахождение площади поверхности и объёма прямоугольного параллелепипеда	Б	1
10	Дроби	Выполнение арифметических действий с десятичными дробями	Б	1
11	Описательная статистика .Комбинаторика.	Извлечение информации из таблицы, диаграммы; выполнение вычислений по табличным данным; выполнение перебора различных вариантов для пересчёта объектов или комбинаций	П	2
12	Работа с текстовыми задачами.	Переход от словесной формулировки соотношений между величинами к алгебраической. Решение текстовых задач алгебраическим способом.	П	2

Вариант

1. Найдите квадрат суммы чисел 154 и 246.

2. На рынке купили 3 кг клубники по ценеа рублей за килограмм, bкг черешни по цене 85 рублей за килограмм и овощей на 147 рублей. Составьте выражение для вычисления стоимости покупки и найдите его значение приа=70, b=2

3. Сколько минут гулял Петя, если от 25 минут составляет 1/6 продолжительности его прогулки?

4. Из дробей ;;; выберите дроби, равные 7.

5. На какое число надо умножить разность чисел 6 и , чтобы получить тот же результат, что и при делении числа 2088 и 12?

6. В квартире, площадь которой равна 80 м², на гостиную приходится 35%, а на кухню – 15% всей площади. На сколько квадратных метров площадь кухни меньше, чем площадь гостиной?

7. Найдите значение выражения 53 кг 410 г – 8 кг 15 г + 120 г – 33 г. Ответ выразите в килограммах и округлите до целых.

8. Туристическая группа за 6 часов преодолела маршрут протяженностью 184 км. Первые 2 часа туристы передвигались на велосипедах со скоростью 18 км/ч. Следующие 2 часа они ехали в автобусе, скорость которого была 68 км/ч. Оставшийся путь туристы прошли пешком. С какой скоростью туристы шли пешком?

9. В ванной комнате пол и стены необходимо покрыть квадратный кафельной плиткой со стороной 15 см. Комната имеет форму прямоугольного параллелепипеда длиной 3 м, шириной 3 м и высотой 2м 70 см. площадь дверного проема равна 18 000 см². Сколько плиток понадобится?

10. Найдите значение выражения (7,6-2,16) • 3,5 : 0,04.

11. У переводчика на столе лежат 4 разных словаря. Сколькими способами эти словари можно сложить в стопку?

12. В трех ящиках 161 кг яблок. В первом ящике в 3 раза больше яблок, чем во втором, а в третьем – на 46 кг больше, чем во втором . Сколько килограммов яблок в каждом ящике?

Приложение №2.

Проблемное обучение при достижении планируемых результатов на уроке математики в 5 классе.

Наша школа является экспериментальной площадкой Московского государственного гуманитарного университета им. М.А. Шолохова по проблеме «Организация учебно-воспитательного процесса в общеобразовательной школе на основе компетентностно-контекстной модели обучения и воспитания», поэтому представим особенности проблемного обучения в рамках данной модели.

Особенности реализации принципа проблемности в компетентностно-контекстной модели образовательного процесса:

1) Цели проблемного обучения (достигаются совместными усилиями обучающего и обучающихся):

- овладение обучающимися знанием, как ориентировочной основой деятельности;

- развитие теоретического мышления;

- формирование познавательной мотивации;

- создание возможностей исследовательского отношения к научному знанию и способам использования его в контексте своего практического действия и поступка.

2) Основная задача обучающего: приобщение обучающихся к противоречиям научного знания, способам их разрешения и использования знания для решения проблем.

3) Основная задача обучаемого: в диалоге (внутреннем и внешнем) с обучающим «открыть» для себя знания как способ полагания себя в будущем (это не одно и тоже, что открыть «ставшие» знания: законы, правила, алгоритмы и т.д., которые являются прошлым чужим опытом).

Организация проблемного обучения в рамках модели компетентностно-контекстного образовательного процесса предполагает реализацию принципа проблемности в содержании обучения и в процессе его развертывания в диалогическом общении обучающего и обучаемого.

4) Содержание проблемного обучения:

- наиболее важное и сложное для понимания и усвоения в контексте его использования;

- отражающие объективные и субъективные противоречия на пути их практической реализации;

- раскрывающие логику появления и суть научной идеи, теории и способов ее использования для решения проблем;

- учитывающие познавательные возможности обучающихся;

- доступное по уровню трудности для понимания обучающимися;

- представленное как основная и соподчиненные ей проблемы и задачи.

5) Способы личностного, диалогического включения обучающего в общение с обучающимися:

- обучающий не «законодатель», а собеседник;

- делится своим личностным и интеллектуальным достоянием, а не «передает» информацию;

- заинтересован в суждениях обучающихся;

- истинность информации демонстрирует посредством доказательства;

- обсуждает разные точки зрения на проблему и ее разрешение;

- подводит обучающихся к самостоятельным выводам, делает их соучастниками поиска разрешения противоречий;

- использует информационные и проблемные вопросы;

- стимулирует поиск обучающимися собственных ответов;

- добивается совместного думания с обучающимися;

- задает проблемные вопросы для обсуждения на последующих занятиях и самостоятельной проработки.

Т.о. в компетентностно-контекстной модели обучения осуществляется внутренний (мысленный) и/или внешний диалог обучающего и обучающихся на проблемно представленном содержании.

Покажем, как реализуется принцип проблемности в содержании обучения и диалогическом общении обучающегося и обучаемого на примере темы «Решение уравнений» в 5 классе.

На доске (плакате или экране) представляется таблица до начала урока. Дети с ней могут познакомиться еще до начала урока. В таблице содержатся все основные понятия об уравнении из начальной школы, которые пока не несут признаков проблемности.

Решение уравнений

x + a = b x - a = b a - x = b x • a = b x : a = b a : x = b

x = b – a x = b + a x = a-b x = b:a x = a•b x = a:b

Учитель начинает урок, с объявления темы. Например, так: тема сегодняшнего урока «Решение уравнений».

А затем с помощью методических приемов строит работу по управлению процессом мышления. К таким приемам относятся:

- постановка проблемных и информационных вопросов;

- выдвижение гипотез, их подтверждение или опровержение;

- побуждение обучающихся к совместному размышлению;

- обращение к обучающимся за помощью;

- ведение минидискуссии с обучающимися.

Прежде, чем представлять дальнейший ход урока определим, что мы понимаем под проблемными и информационными вопросами как средством управления мыслительной деятельностью обучающихся:

- информационные вопросы - направлены в «прошлое», к усвоенному на предшествующих занятиях материалу;

- проблемные вопросы – направлены в будущее, к тому неизвестному (обучающемуся), новому (для обучающегося) знанию, как средству собственного действия и поступка.

Вернемся к уроку. После объявления темы учитель обращает внимание учащихся на другую запись на доске (или экране). Причем таблица с видами уравнений так же находится перед учащимися.

х+15 = 75; y – 15 = 75; h -15:3; (27 + 35) – 15; k+2•18

60 – z = 15; а+34+23; b • 15 = 45; c : 15 = 3; 60 : d = 15; 2(5x + 3) = 26

Учитель обращает внимание учащихся на ряд указанных выражений и предлагает в совместной деятельности выполнить следующее задание: Среди указанных выражений найдите уравнения и решите их.

Выполнение этого задания организуется в форме фронтальной работы с использованием информационных вопросов (тех, на которые учащиеся могут ответить на основе уже имеющихся знаний). Так как на данном этапе организуется свободный диалог, то его трудно запротоколировать. Можно только описать примерный ход варианта одной из минидискуссий:

Учитель: Что вы можете сказать по поводу первого выражения в свете решаемой задачи: х+15 = 75?

Примерный вариант разворачивания минидискуссии:

Ученик: это уравнение.

Учитель: как Вы можете доказать свою точку зрения?

Ученик: Уравнение – это равенство, содержащее переменную.

Учитель: Можете ли Вы решить данное уравнение?

Ученик: Да. Х = 60

Учитель: Объясните, как вы нашли данный ответ, и как его можно назвать.

Ученик: В данном уравнении неизвестным является слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Найденное число, называется корнем уравнения.

Приведенный диалог разворачивается на информационных вопросах. В нем участвуют все учащиеся. Вполне возможно, что на некоторые вопросы отвечают хором. Если затрудняются при ответе, учитель напоминает необходимые правила. Поправляет некорректные ответы и речевые ошибки. Диалог как правило проходит динамично, все вовлечены в разговор, так как понимаю о чем речь, им нравится показать свои знания и быть успешными.

По такому же сценарию разворачивается беседа по каждому выражению. Только уже в сжатой форме. Например,

Учитель: что Вы можете сказать по поводу второго выражения: y – 15 = 75?

Ученик: это уравнение, так как содержит равенство с переменной. Неизвестным является уменьшаемое. Чтобы его найти, нужно к разности прибавить вычитаемое. Корень уравнения: 90.

Или

Ученик: h -15:3 – не является уравнением, так как содержит переменную, но нет равенства. Это буквенное выражение.

При анализе последнего выражения 2(5x + 3) = 26 учащиеся делают вывод, что перед ними уравнение. Но вопрос, как его решить. Неважно поставлен ли он учителем или самим учащимся, является проблемным, так как у них нет знаний по способам решения данных уравнений.

Учитель побуждает учащихся к совместному поиску метода решения данного уравнения и предлагает высказать гипотезы.

Каковы бы не были гипотезы детей. Учитель обсуждает их с одной точки зрения: никаких других правил решения уравнений у нас, кроме записанных на доске нет. Проанализируй (или докажи), что предложенный вариант строится на данных правилах.

Задача диалога на данном этапе урока: раскрыть перед учащимися логику и суть научной идеи (решения уравнений с помощью использования связи между компонентами действий) и способов ее использования для решения проблем (в данном случае нового вида уравнений). То есть с данного момента урока привычное содержание стало для обучающихся проблемным. Диалог на данном этапе протоколировать практически невозможно, он развивается в указанной выше логике, но результат его следующий.

Учитель резюмирует результат дискуссии в виде следующего алгоритма.

1. Убедиться, что решаемое уравнение имеет вид:

x + a = b, x - a = b, a - x = b, x • a = b, x : a = b, a : x = b, где в качестве неизвестного может выступать выражение, содержащее переменную.

2. Применить соответствующее правило нахождения неизвестного компонента действия.

3. Применить п.п.1 и 2 до тех пор, пока не будет найдено значение неизвестной переменной.

4. Записать ответ.

Дальнейшее продолжение урока строится на основе проблемного содержания, так как сам обобщенный алгоритм содержит в себе проблемность: как его применять? К какому классу задач? Как определить, что в данной ситуации применим именно данный алгоритм действия?

Учитель предлагает учащимся еще ряд выражений:

1) х + (1200-900) = 1500

2) (50 • 30) : y = 15

3) 432:36 – n = 11

4) m • (16 + 32) = 1920

5) 27х -14х + 38 +15х = 990

6) 1620 : (19 – х : 36) = 10

7) (16х – 10х + 3) = 132

8) (346 – (х : 16 - 398)) : 7 = 42

9) (7z – 93) : 48 : 8 = 24:12

А задание решить данные уравнения создает проблемную ситуацию –состояние мыслительного взаимодействия человека с предметом познания, направленного на поиск, «открытие» и овладение новым знанием относительно научных фактов, принципов, закономерностей и условий собственного действия и поступка.

Субъективными признаками проблемной ситуации являются:

- переживание интеллектуального затруднения в условиях собственного действия и поступка;

- вопрос к себе о неизвестном знании, способе или условии действия или поступка.

Учащиеся оказываются в проблемной ситуации при решении указанных уравнений в процессе фронтальной работы.

Учитель также как и в начале урока предлагает решить учащимся уравнения. Однако в данном случае вопрос относительно каждого уравнения «Как решить это уравнение?» носит не информационный, а проблемный характер. Несмотря на то, что алгоритм решения и основные правила нахождения неизвестного компонента действия известны, решение каждого из предложенных уравнений переводит проблемную ситуацию

в результате анализа ее условий в проблему, которая фиксирует противоречивость теоретической или практической ситуации, ее компонентов и условий. Проблема и является основной единицей содержания компетентностно-контекстной модели обучения.

В рассматриваемом случае, при решении каждого из предложенных уравнений, основной проблемой является поиск способа применения известного алгоритма и правил в конкретной ситуации.

Приведем пример возможной минидискуссии обучающего и обучающихся:

Учитель: Как будем решать уравнение 27х -14х + 38 +15х = 990?

Ученик: данное уравнение не является уравнением одного из искомых видов.

Учитель: ваши предложения по сведению его к искомому виду.

Ученик: можно попробовать упростить левую часть уравнения, тогда мы получим уравнение вида: 28х + 38 = 990. Данное уравнение является уравнением вида: x + a = b, где в качестве неизвестного слагаемого выступает выражение 28х.

Тогда 28х = 990 – 38; 28х = 952.

Мы получили уравнение вида: x • a = b.

х = 952 : 28; х = 34.

На этом совместная деятельность обучающего и обучающих завершается.

Необходимо только отметить формы активности субъектов деятельности:

- обучающий с помощью выше указанных педагогических средств (проблемного содержания, информационных и проблемных вопросов и т.д.) управлял мышлением обучающихся;

- обучающийся проявлял такие формы активности как:

- активное слушание и понимание;

- ведение записей;

- постановка вопросов обучающему или другому обчающемуся, или самому себе для последующего поиска ответов.

После того, как все уравнения решены в совместной деятельности обучающего и обучающихся, учитель предлагает выполнить следующие задания:

1) с : (1200 : 2) = 3

2) z + 42 • 9 = 630

3) (524 - m) – 133 = 207

4) 927 - (627 + n) = 349

5) 2(6х + 8) – 3х = 3

6) 630 : (63х - 42х) + 53 = 68

7) 78 + (84 - m) – 13 = 92

8) 69 – (97 - (28 +n)) = 45

9) Числа x и y связаны формулой y = 3(7x +6) найдите х, если y = 122

10) Какие из чисел 2, 4, 6 являются корнями уравнения х + 8 : х = 6

11) Задумали некоторое число. Разность задуманного числа и 56 больше суммы 45 и 32 на 17. Найдите задуманное число.

12) Каким числом необходимо заменить а, чтобы корнем уравнения 35 – (а + 12) = х + 12 было число 7?

13) Известно, что y =(2x – a):b выразите a, в и х из этой формулы.

14) При каком значении переменой 35 и 7х меньше 23х на 29?

15) Какими натуральными числами необходимо заменить a и b, чтобы корнем уравнения (х - а) + (12 - b) = 18 было число 8?

Данное задание выполняется обучаюшимися самостоятельно в коллективной деятельности. Повторимся и акцентируем внимание на том факте, что содержание несет в себе проблемность относительно способов использования знания в конкретной ситуации и выполняется вновь в диалоге, только на уровне ученик-ученик. Обучающий выступает на данном этапе тьютором, сопровождающим процесс самореализации обучающихся.

В заключении отметим, что эффективность проблемного обучения в компетентностно-контекстной модели обучения определяется:

- педагогическим мастерством обучающего;

- методически грамотной реализацией принципа проблемности в содержании;

- личностным, пристрастным отношением обучающеего к содержанию;

- организацией продуктивного диалога с обучающимися;

- отражением в содержании предметного и инструментального контекста деятельности;

- обеспечением условий, порождающих личностно-смысловое отношение обучающихся к содержанию усваиваемого материала в противовес пассивному слушанию.

И подчеркнем закономерность: чем выше диалогичность (внутренняя и /или внешняя) обучения, тем выше его эффективность

20