6
Муниципальное автономное общеобразовательное учреждение
«Лицей № 78 имени А.С.Пушкина»
III ОТКРЫТАЯ НАУЧНО-ПРАКТИЧЕСКАЯ
КОНФЕРЕНЦИЯ «ЭВРИКА»
Направление (секция): Математика
Проектная работа :
Теория округленной степени натурального числа
Гилязиев Наиль , Сидоров Артур, Редько Артемий
МАОУ «Лицей №78 им. А.С.Пушкина», 5 класс
город Набережные Челны Республики Татарстан
Научный руководитель: Бубнова Елена Витальевна
Учитель высшей квалификационной категории
г. Набережные Челны
2014
Оглавление
Введение 3
Что такое округлённая степень натурального числа? 4
Опыт 1 4
Опыт 2 4
Опыт 3 5
Заключение 5
Введение
Актуальность темы:
Ускорение процесса подсчета на крупных предприятиях, в торговле, в образовании, что поможет повысить качество работы.
Цель работы:
Объяснить и показать, как можно облегчить подсчет при работе с круглыми числами на предприятиях и в школах.
Задачи работы:
1. Доказать, что теория округленных степеней натурального числа верна.
2. Облегчить математический счет.
Практическая значимость:
Округленная степень натурального числа может быть использована в сфере деятельности человека.
Научная новизна:
Используя таблицу степеней натурального числа, мы внесли дополнительный фактор, с помощью которого результаты табличных значений привели к круглым числам.
Объект и предмет исследования:
Математические выражения и округлённые степени натурального числа.
Методы исследования:
1.Проведение опытов;
2.Анализ полученных результатов;
Гипотеза:
Знание округлённой степени натурального числа поможет ускорить процесс подсчета на крупных предприятиях, в торговле, в образовании, что поможет повысить качество работы.
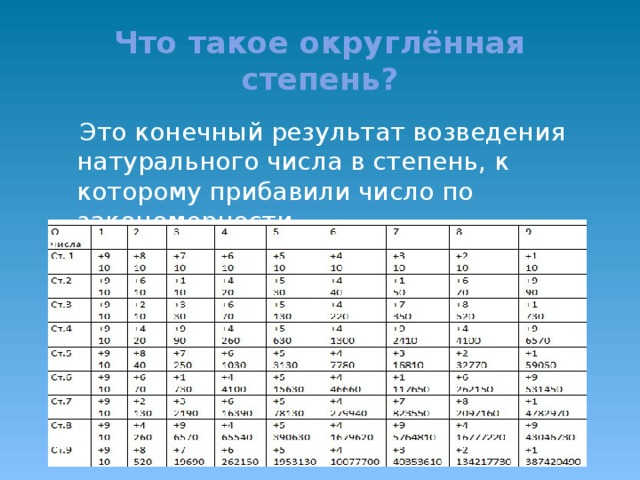
Что такое округлённая степень натурального числа?
Округленная степень натурального числа - это конечный результат возведения натурального числа в степень, к которому прибавили число по закономерности .
У округлённой степени натурального числа есть две закономерности: числовая и со степенями.
Ход работы.
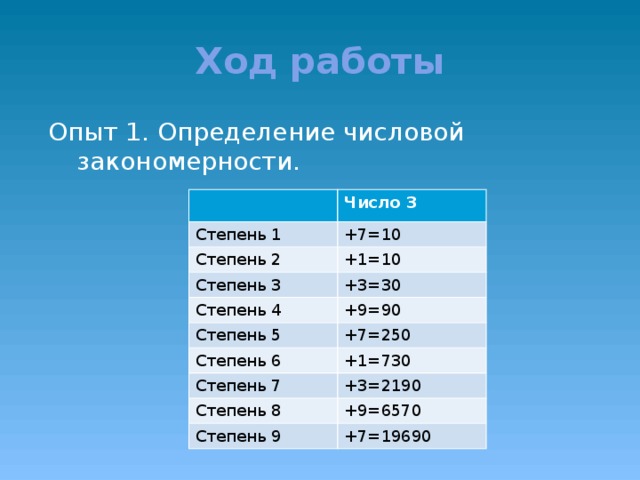
Опыт 1. Числовая закономерность.
Когда мы решали примеры, то увидели, что числа повторяются в определённой последовательности. Мы заинтересовались и решили проверить, действует ли эта закономерность на других числах.
У каждого числа своя последовательность,
У числа 1 закономерность +9+9+9+9…
У числа 2 закономерность +8+6+2+4…
У числа 3 закономерность +7+1+3+9…
У числа 4 закономерность +6+4+6+4…
У числа 5 закономерность +5+5+5+5…
У числа 6 закономерность +4+4+4+4…
У числа 7 закономерность +3+1+7+9…
У числа 8 закономерность +2+6+8+4…
У числа 9 закономерность +1+9+1+9…
(Приложение. Презентация. Слайд 11)
Вывод. Группа чисел повторяется через каждые 4 числа, т.е. действует числовая закономерность.
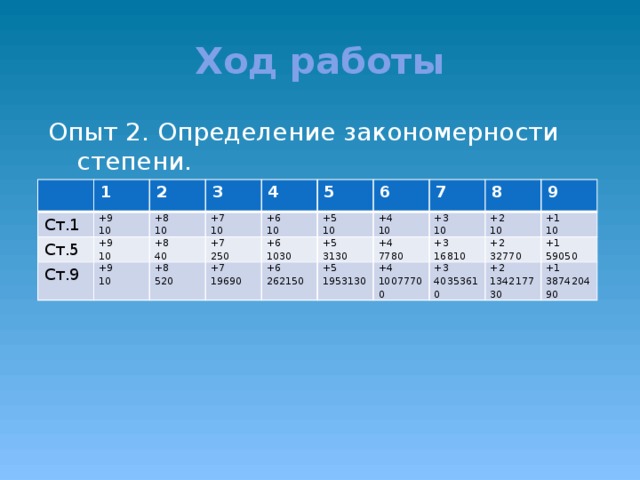
Опыт 2. Закономерность со степенями.
Когда мы рассматривали таблицу степеней натуральных чисел , то заметили, что некоторые ряды совпадают по последовательности чисел.
У степени 1,5,9 ряд +9+8+7+6+5+4+3+2+1
У степени 4,8 ряд +9+4+9+4+5+9+4+9+4
У степени 3,7 ряд +9+2+3+6+5+4+7+8+1
(Приложение. Презентация. Слайд 12)
Вывод. В определённых рядах повторяется последовательность чисел, то есть действует закономерность со степенями.
Опыт 3.Анкетирование.
Мы провели анкетирование среди учащихся 5»В» класса. Был предложен пример и 3 вопроса к нему.
Решите пример:
(3+4) в степени 7, результат нужно округлить.
1.Какое число вы прибавили, чтобы округлить полученный результат?
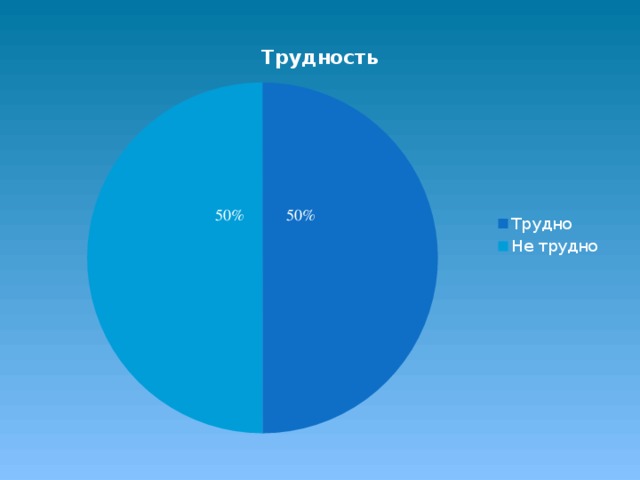
2.Было ли вам трудно решать пример?
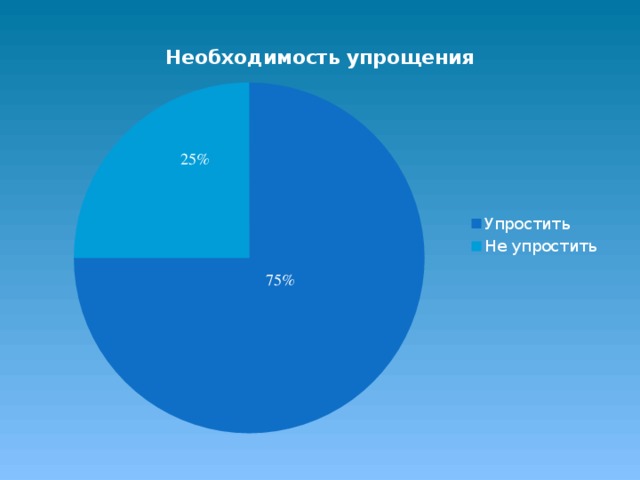
3.Хотели бы вы это упростить?
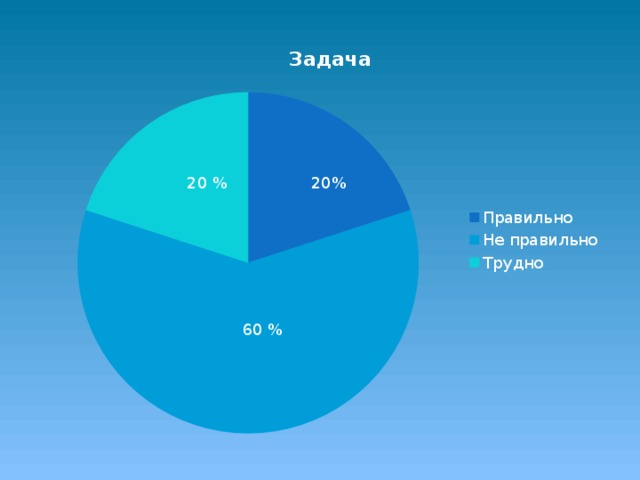
По результатам 1 вопроса мы выяснили, что 20% учащихся ответили верно, 60% ответили неверно и 20% ответили, что не могут решить.
По результатам 2 вопроса выяснилось, что 50% было трудно решать пример, а остальные 50% ответили, что им было легко.
На третий вопрос 25% ответили, что не хотели бы упростить пример, а 75% хотели бы упростить пример.
(Приложение. Презентация. Слайд 13,14,15,16)
Вывод: Большинству учащихся было сложно решить эту задачу, то есть нужно упростить задачу.
Заключение
Знание округлённой степени натурального числа поможет облегчить математический счет на предприятиях, в торговле, в образовании и в других сферах деятельности человека.
