Наглядные материалы содержат презентацию и опорный конспект по теме "Квадратичная функция". В презентации представлены:
- Построение графиков квадратичной функции у = kx2;
- Наглядно показана зависимость параболы от коэффициента k;
- Свойства квадратичной функции (область определения, непрерывность, монотонность, ограниченность, наибольшие и наименьшие значения, область значений, выпуклость функции)
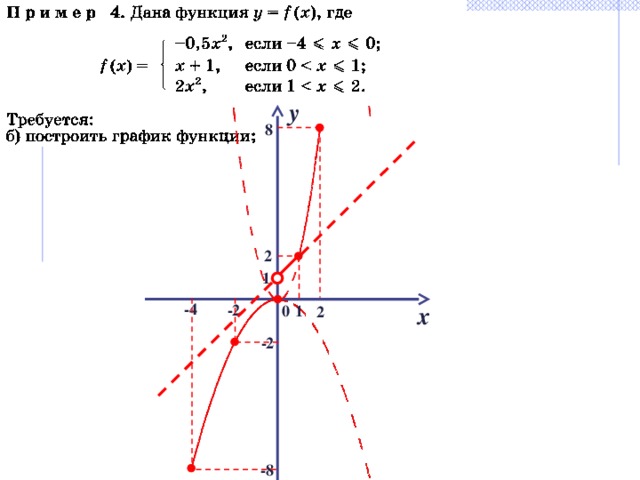
- Пример построения и описания свойств кусочной функции
Опорный конспект содержит описание свойств квадратичной функции
Просмотр содержимого документа
«опорный конспект»
Просмотр содержимого презентации
«Квадратичная функция»

Квадратичная функция y = kx 2 , её свойства и график
Автор: учитель математики Д.И. Мотырев
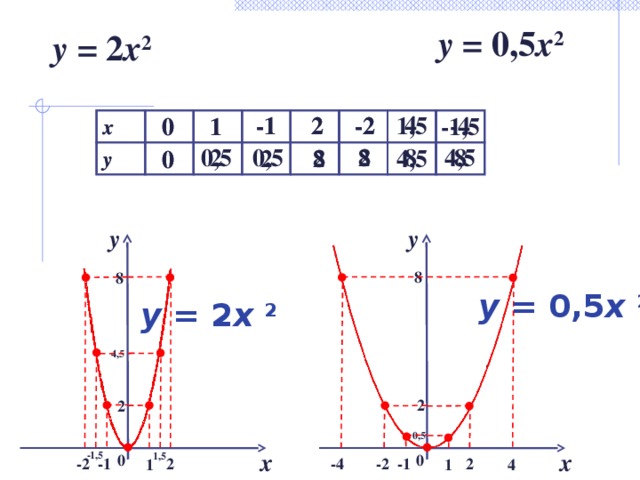
y = 0,5 x 2
y = 2 x 2
4
-4
2
2
-1
-1
1,5
-2
-2
1
1
-1,5
0
0
x
x
y
y
8
2
8
2
0,5
0,5
8
4,5
2
8
2
4,5
0
0
y
y
8
8
y = 0,5 x 2
y = 2 x 2
4,5
2
2
0,5
x
x
-1,5
1,5
0
0
2
2
-2
-2
-1
-4
-1
1
1
4
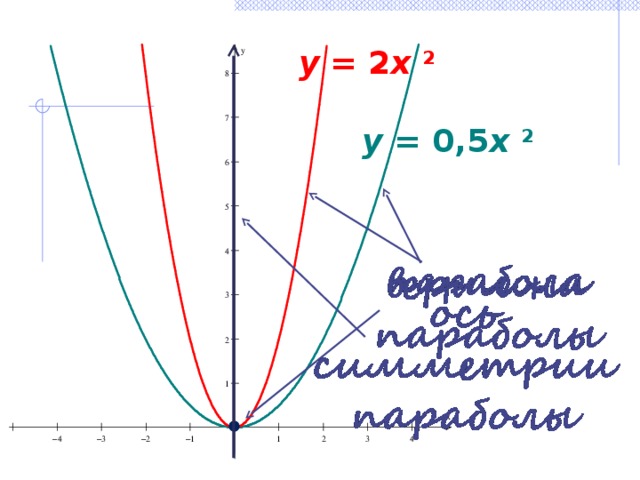
y = 2 x 2
y = 0,5 x 2
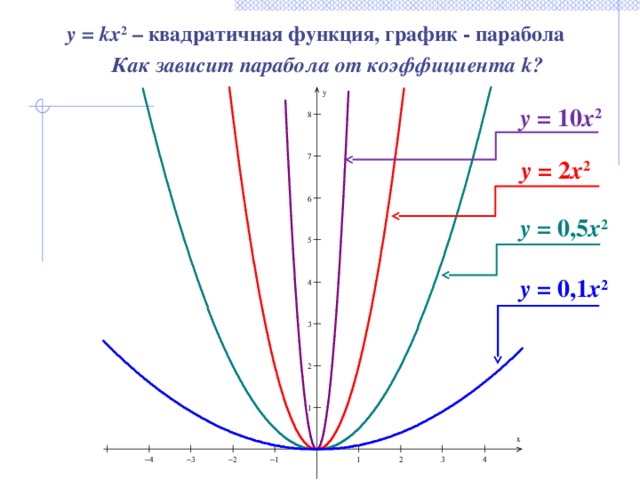
у = kx 2 – квадратичная функция, график - парабола
Как зависит парабола от коэффициента k?
y = 10 x 2
y = 2 x 2
y = 0,5 x 2
y = 0,1 x 2
2
2
-1
-1
1,5
-2
-2
1
1
-1,5
0
0
x
y
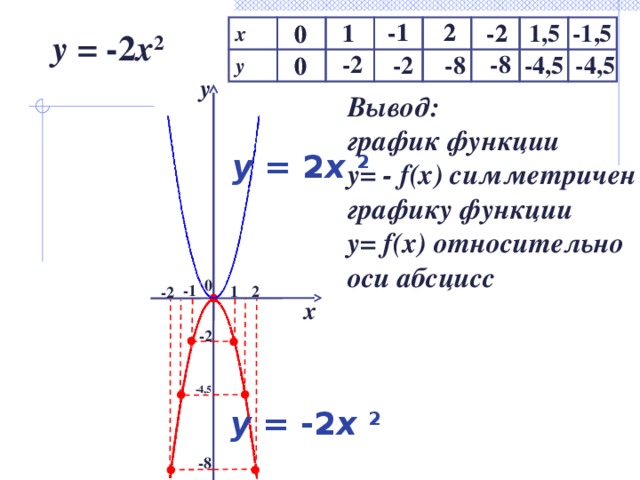
y = -2 x 2
-8
-2
-4,5
-8
-2
-4,5
0
0
y
Вывод:
график функции
y= - f(x) симметричен
графику функции
y= f(x) относительно
оси абсцисс
y = 2 x 2
0
-1
1
2
-2
x
-2
-4,5
y = -2 x 2
-8
 0 ⇒ ветви параболы направлены вверх x y k ⇒ ветви параболы направлены вниз x" width="640"
0 ⇒ ветви параболы направлены вверх x y k ⇒ ветви параболы направлены вниз x" width="640"
y
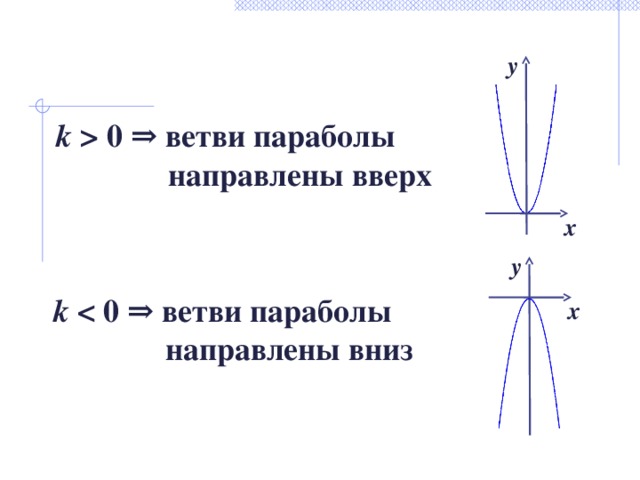
k 0 ⇒ ветви параболы
направлены вверх
x
y
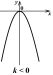
k ⇒ ветви параболы
направлены вниз
x
 0 y y x x D(y) = ( - ∞; +∞ )" width="640"
0 y y x x D(y) = ( - ∞; +∞ )" width="640"
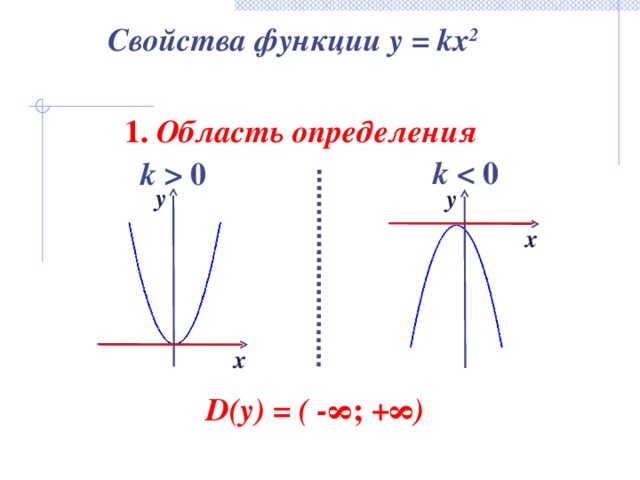
Свойства функции y = kx 2
1. Область определения
k 0
k 0
y
y
x
x
D(y) = ( - ∞; +∞ )
 0 y y x x Функция непрерывна" width="640"
0 y y x x Функция непрерывна" width="640"
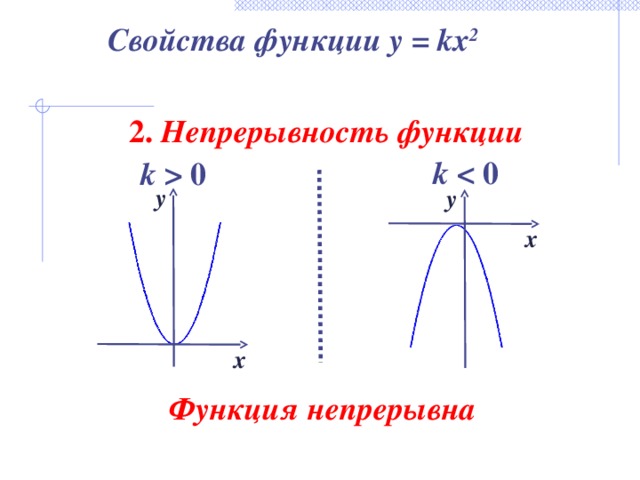
Свойства функции y = kx 2
2. Непрерывность функции
k 0
k 0
y
y
x
x
Функция непрерывна
 0 y y 0 x 0 x Функция убывает при х 0 Функция возрастает при х 0 Функция возрастает при х 0 Функция убывает при х 0" width="640"
0 y y 0 x 0 x Функция убывает при х 0 Функция возрастает при х 0 Функция возрастает при х 0 Функция убывает при х 0" width="640"
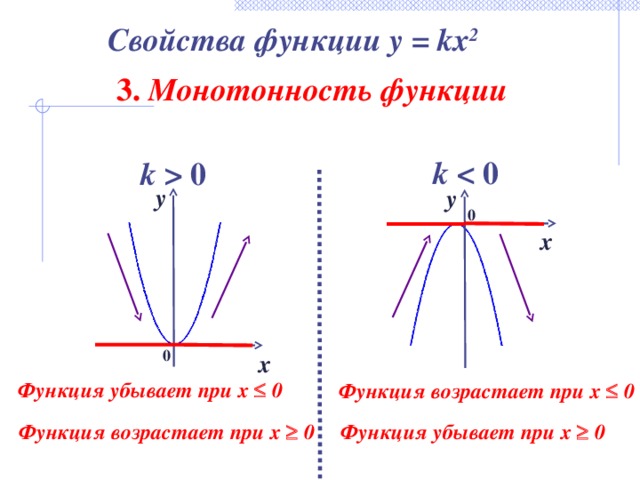
Свойства функции y = kx 2
3. Монотонность функции
k 0
k 0
y
y
0
x
0
x
Функция убывает при х 0
Функция возрастает при х 0
Функция возрастает при х 0
Функция убывает при х 0
 0 y y x x Функция ограничена снизу Функция не ограничена снизу и не ограничена сверху и ограничена сверху" width="640"
0 y y x x Функция ограничена снизу Функция не ограничена снизу и не ограничена сверху и ограничена сверху" width="640"
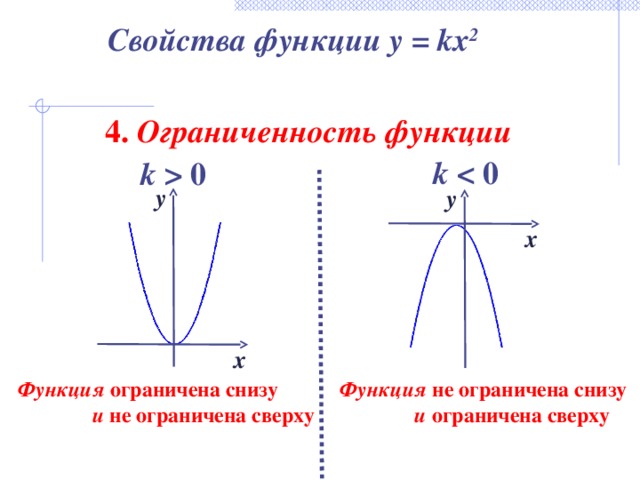
Свойства функции y = kx 2
4. Ограниченность функции
k 0
k 0
y
y
x
x
Функция ограничена снизу
Функция не ограничена снизу
и не ограничена сверху
и ограничена сверху
 0 y y x x у наиб не существует у наиб = 0 у наим = 0 у наим не существует" width="640"
0 y y x x у наиб не существует у наиб = 0 у наим = 0 у наим не существует" width="640"
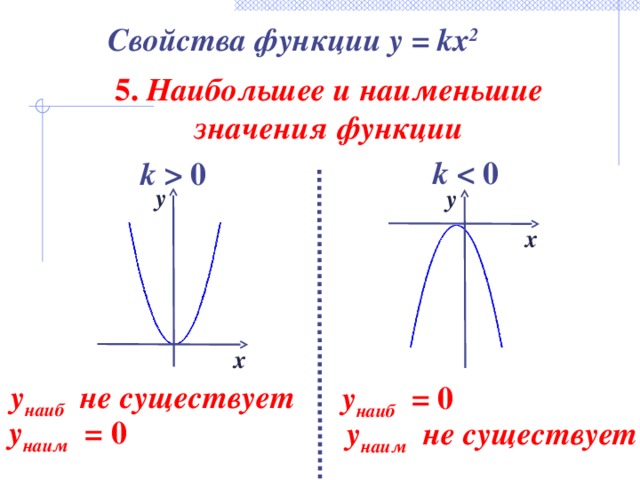
Свойства функции y = kx 2
5. Наибольшее и наименьшие
значения функции
k 0
k 0
y
y
x
x
у наиб не существует
у наиб = 0
у наим = 0
у наим не существует
 0 y y 0 x x 0 Е(y) = ( -∞; 0] Е(y) = [ 0; +∞)" width="640"
0 y y 0 x x 0 Е(y) = ( -∞; 0] Е(y) = [ 0; +∞)" width="640"
Свойства функции y = kx 2
6. Область значений функции
k 0
k 0
y
y
0
x
x
0
Е(y) = ( -∞; 0]
Е(y) = [ 0; +∞)
 0 y y 0 x график выше отрезка график выше отрезка график ниже отрезка график ниже отрезка x 0 Функция выпукла вверх Функция выпукла вниз" width="640"
0 y y 0 x график выше отрезка график выше отрезка график ниже отрезка график ниже отрезка x 0 Функция выпукла вверх Функция выпукла вниз" width="640"
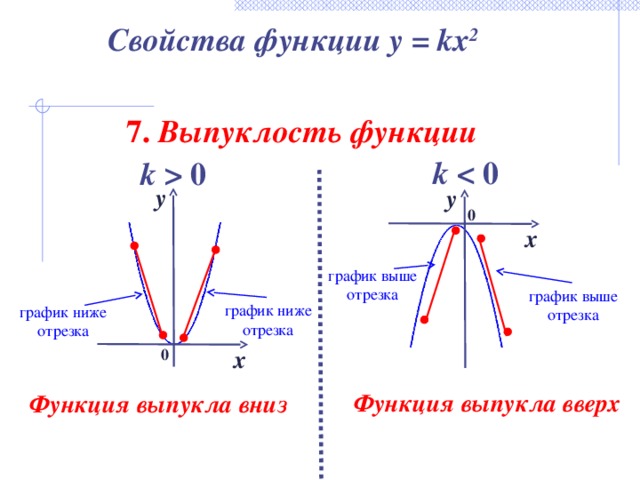
Свойства функции y = kx 2
7. Выпуклость функции
k 0
k 0
y
y
0
x
график выше
отрезка
график выше
отрезка
график ниже
отрезка
график ниже
отрезка
x
0
Функция выпукла вверх
Функция выпукла вниз

![Решение: -4 [ -4 ; 0 ] ⇒ f (-4) = -0,5 ∙ (-4) 2 = -0,5 ∙ 16 = - 8 -2 [ -4 ; 0 ] ⇒ f (-2) = -0,5 ∙ (-2) 2 = -0,5 ∙ 4 = - 2 0 [ -4 ; 0 ] ⇒ f (0) = -0,5 ∙ 0 2 = -0,5 ∙ 0 = 0 ( 0 ; 1 ] ⇒ f ( ) = + 1 = 1,5 ( 1 ; 2 ] ⇒ f ( ) = 2 ∙ = 2 ∙ 2 = 4 2 ( 1 ; 2 ] ⇒ f (2) = 2 ∙ 2 2 = 2 ∙ 4 = 8 3 D ( f ) ⇒ f (3) нельзя вычислить (задание некорректно)](https://fsd.kopilkaurokov.ru/uploads/user_file_5617371c46a6c/img_user_file_5617371c46a6c_0_14.jpg)
Решение:
-4 [ -4 ; 0 ] ⇒ f (-4) = -0,5 ∙ (-4) 2 = -0,5 ∙ 16 = - 8
-2 [ -4 ; 0 ] ⇒ f (-2) = -0,5 ∙ (-2) 2 = -0,5 ∙ 4 = - 2
0 [ -4 ; 0 ] ⇒ f (0) = -0,5 ∙ 0 2 = -0,5 ∙ 0 = 0
( 0 ; 1 ] ⇒ f ( ) = + 1 = 1,5
( 1 ; 2 ] ⇒ f ( ) = 2 ∙ = 2 ∙ 2 = 4
2 ( 1 ; 2 ] ⇒ f (2) = 2 ∙ 2 2 = 2 ∙ 4 = 8
3 D ( f ) ⇒ f (3) нельзя вычислить (задание некорректно)
y
8
2
1
-4
-2
x
0
1
2
-2
-8
![Свойства функции: y 1. Область определения 7. Выпуклость функции 8 D( f ) = [ - 4 ; 2 ] При х [ - 4 ; 0 ] функция выпукла вверх 2. Непрерывность функции При х ( 0 ; 1 ] функция не выпукла Функция имеет разрыв при х = 0 3. Монотонность функции 2 При х [ 1 ; 2 ] функция выпукла вниз Функция возрастает на D( f ) 1 4. Ограниченность функции x -4 0 1 2 Функция ограничена снизу и сверху 5. Наибольшее и наименьшее значения функции = - 8 у min = у(-4) у max = у(2) = 8 6. Область значений функции E( f ) = [ - 8 ; 0 ] ( 1 ; 8 ] -8](https://fsd.kopilkaurokov.ru/uploads/user_file_5617371c46a6c/img_user_file_5617371c46a6c_0_16.jpg)
Свойства функции:
y
1. Область определения
7. Выпуклость функции
8
D( f ) = [ - 4 ; 2 ]
При х [ - 4 ; 0 ] функция
выпукла вверх
2. Непрерывность функции
При х ( 0 ; 1 ] функция
не выпукла
Функция имеет разрыв при х = 0
3. Монотонность функции
2
При х [ 1 ; 2 ] функция
выпукла вниз
Функция возрастает на D( f )
1
4. Ограниченность функции
x
-4
0
1
2
Функция ограничена снизу и сверху
5. Наибольшее и наименьшее
значения функции
= - 8
у min = у(-4)
у max = у(2)
= 8
6. Область значений функции
E( f ) = [ - 8 ; 0 ] ( 1 ; 8 ]
-8
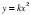 , её свойства и график
, её свойства и график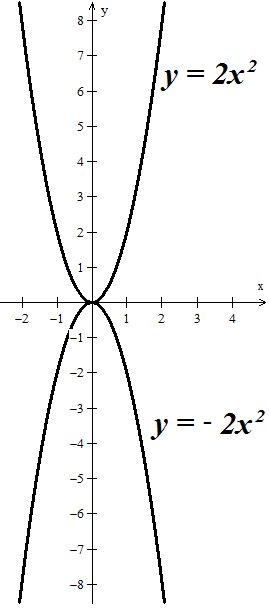
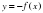 симметричен графику функции
симметричен графику функции 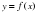 относительно оси абсцисс (оси Ох)
относительно оси абсцисс (оси Ох)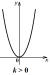
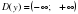
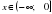
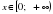
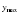 не существует
не существует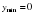
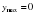
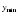 не существует
не существует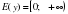
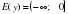





 0 ⇒ ветви параболы направлены вверх x y k ⇒ ветви параболы направлены вниз x" width="640"
0 ⇒ ветви параболы направлены вверх x y k ⇒ ветви параболы направлены вниз x" width="640"
 0 y y x x D(y) = ( - ∞; +∞ )" width="640"
0 y y x x D(y) = ( - ∞; +∞ )" width="640"
 0 y y x x Функция непрерывна" width="640"
0 y y x x Функция непрерывна" width="640"
 0 y y 0 x 0 x Функция убывает при х 0 Функция возрастает при х 0 Функция возрастает при х 0 Функция убывает при х 0" width="640"
0 y y 0 x 0 x Функция убывает при х 0 Функция возрастает при х 0 Функция возрастает при х 0 Функция убывает при х 0" width="640"
 0 y y x x Функция ограничена снизу Функция не ограничена снизу и не ограничена сверху и ограничена сверху" width="640"
0 y y x x Функция ограничена снизу Функция не ограничена снизу и не ограничена сверху и ограничена сверху" width="640"
 0 y y x x у наиб не существует у наиб = 0 у наим = 0 у наим не существует" width="640"
0 y y x x у наиб не существует у наиб = 0 у наим = 0 у наим не существует" width="640"
 0 y y 0 x x 0 Е(y) = ( -∞; 0] Е(y) = [ 0; +∞)" width="640"
0 y y 0 x x 0 Е(y) = ( -∞; 0] Е(y) = [ 0; +∞)" width="640"
 0 y y 0 x график выше отрезка график выше отрезка график ниже отрезка график ниже отрезка x 0 Функция выпукла вверх Функция выпукла вниз" width="640"
0 y y 0 x график выше отрезка график выше отрезка график ниже отрезка график ниже отрезка x 0 Функция выпукла вверх Функция выпукла вниз" width="640"

![Решение: -4 [ -4 ; 0 ] ⇒ f (-4) = -0,5 ∙ (-4) 2 = -0,5 ∙ 16 = - 8 -2 [ -4 ; 0 ] ⇒ f (-2) = -0,5 ∙ (-2) 2 = -0,5 ∙ 4 = - 2 0 [ -4 ; 0 ] ⇒ f (0) = -0,5 ∙ 0 2 = -0,5 ∙ 0 = 0 ( 0 ; 1 ] ⇒ f ( ) = + 1 = 1,5 ( 1 ; 2 ] ⇒ f ( ) = 2 ∙ = 2 ∙ 2 = 4 2 ( 1 ; 2 ] ⇒ f (2) = 2 ∙ 2 2 = 2 ∙ 4 = 8 3 D ( f ) ⇒ f (3) нельзя вычислить (задание некорректно)](https://fsd.kopilkaurokov.ru/uploads/user_file_5617371c46a6c/img_user_file_5617371c46a6c_0_14.jpg)

![Свойства функции: y 1. Область определения 7. Выпуклость функции 8 D( f ) = [ - 4 ; 2 ] При х [ - 4 ; 0 ] функция выпукла вверх 2. Непрерывность функции При х ( 0 ; 1 ] функция не выпукла Функция имеет разрыв при х = 0 3. Монотонность функции 2 При х [ 1 ; 2 ] функция выпукла вниз Функция возрастает на D( f ) 1 4. Ограниченность функции x -4 0 1 2 Функция ограничена снизу и сверху 5. Наибольшее и наименьшее значения функции = - 8 у min = у(-4) у max = у(2) = 8 6. Область значений функции E( f ) = [ - 8 ; 0 ] ( 1 ; 8 ] -8](https://fsd.kopilkaurokov.ru/uploads/user_file_5617371c46a6c/img_user_file_5617371c46a6c_0_16.jpg)
















