Содержание:
Информация об опыте…………2
Технология опыта………………2-4
Результативность опыта……… 4
Библиографический список…...5
Рецензия на опыт работы…… 6
Приложения к опыту ………….. 7-15
Приложение №1 – Принцип составления заданий
Приложение №2 – Мониторинг
Приложение №3 – Комплект зачётов для 6 класса (система зачётов).
Приложение №4 – Индивидуальная карта «проблемных» заданий
Иванушкина Ирина Геннадьевна, учитель математики МБОУ ООШ №7 МО Абинский район.
Тема опыта: «Мониторинг зачетов в системе дифференцированного обучения математике».
Важным звеном процесса обучения математике является контроль знаний и умений школьников. От того, как он организован, на что нацелен, существенно зависит эффективность учебной работы. Именно поэтому я на практике уделяю серьезное внимание способам организации контроля, его содержанию и мониторингу. Моя работа всегда связана со стремлением более полно реализовать цели и задачи школьного математического образования, она отражает те или иные изменения, которые происходят в системе обучения математике. Я работаю в сельской малокомплектной школе, где обучаются дети из трёх маленьких населённых пунктов, т.е. время пребывания многих из них в школе ограничено, так как 80% детей приезжают в школу на автобусе. Поэтому нет возможности заниматься математикой дополнительно больше времени, всё приходится делать в основном на уроках. Поэтому возникла идея, так, сказать держать знания учащихся под контролем.
В настоящее время принципиальные изменения в школе связаны в первую очередь с введением дифференцированного обучения. Важнейшим видом дифференциации при обучении во всех классах становится уровневая дифференциация. Ее основная особенность состоит в дифференциации требований к знаниям и умениям учащихся: явно выделяется уровень обязательной подготовки, который задает достаточную нижнюю границу усвоения материала. Этот уровень, безусловно, доступен и посилен всем школьникам. На его основе я формирую повышенные уровни овладения курсом. Мои учащиеся получают право и возможность, обучаясь в одном классе и по одной программе, выбирать тот уровень усвоения, который соответствует их потребностям, интересам, способностям.
При создании системы зачётов необходимо признать, что каждый ученик имеет право сам, добровольно выбирать для себя уровень усвоения и отчетности в результатах своего учебного труда. Я убеждена, что такой подход способствует психологическому комфорту ученика в школе, формирует у него чувство уважения к себе и к окружающим, вырабатывает ответственность и способность к принятию решений.
Традиционно контрольные работы я составляла таким образом, что все задания в них были ориентированы на «пятерочный» уровень и каждое проверяло применение целой совокупности умений. Задачи, непосредственно направленные на проверку овладения опорными умениями, в них, как правило, отсутствовали.
Например, умение решать квадратные уравнения проверялось через задачу типа: «При каких значениях к уравнение кх2- 6х + к = 0 имеет два корня?»
Результаты такого контроля могли дать позитивную информацию только о подготовке учащихся, полностью справившихся с предложенными заданиями. В отношении же тех, которые не могут их выполнить, можно сказать лишь то, что они чего-то не знают и не умеют; судить же об истинном содержании и уровне их знаний трудно. Например, если ученик не сумел решить приведенную выше задачу, то я могла так и не выяснить, умеет ли он решать стандартные квадратные уравнения.
Альтернативой традиционной форме контроля для меня является оценка методом «сложения», в основу которой кладется минимальный уровень общеобразовательной подготовки. Достижение этого уровня требуется от каждого учащегося в обязательном порядке. Критерии оценок более высоких уровней формируются на базе минимального посредством содержательного приращения по глубине или объему усвоения.
Цели уровневой дифференциации состоят в обеспечении достижения всеми школьниками базового уровня подготовки, представляющего собой государственный стандарт образования, и одновременном создании условий для развития учащихся, проявляющих интерес и способности к математике. В соответствии с этим и контроль должен иметь двухступенчатую структуру. А именно в контроле необходимо выделять два принципиальных этапа: проверку достижения уровня обязательной подготовки и проверку на повышенном уровне (Приложение 1, принцип составления зачетной (проверочной) работы). В обязательную часть включаются задачи из списка обязанных результатов обучения или аналогичные им. Понятно, что в один вариант невозможно включить все задачи списка. Однако я того, чтобы обеспечить как можно большую полноту проверки, надо шире охватить все группы умений, представленных на уровне обязательной подготовки. В приведенной работе присутствуют все основные умения по проверяемой теме: решение линейных неравенств (причем предусмотрены случаи деления обеих частей неравенства как на положительное, так и на отрицательное числа, а также необходимость выполнения некоторых тождественных преобразований), решение систем линейных неравенств одной переменной, решение систем, записанных в виде двойного неравенства. Поэтому если ученик справился со всеми задачами первой части работы, то можно с уверенностью сказать, что он овладел материалом на уровне обязательной подготовки.
Учащимся предлагается единая проверочная работа, состоящая из двух дополняющих друг друга частей: одна из них содержит задачи, соответствующие обязательным результатам обучения, другая — задачи повышенного уровня сложности. Важным в выделенном положении является не организационная форма, а то, чтобы каждый ученик прошел через проверку достижения обязательных результатов обучения и имел возможность проявить себя на повышенном уровне (система зачетов для 6 класса, приложение 3).
Именно такой подход обеспечивает замену оценивания методом «вычитания» оцениванием методом «сложения».
Достоинство оценки «сложением» вытекает из ее сути. Главное, пожалуй, заключается в том, что в школу возвращается мотивация учебного успеха. Не менее важна возможность гарантированной опоры на достигнутый базовый уровень подготовки. Посильность этого уровня для всех учащихся делает ненужной «выводиловку», а возможность последовательного приращения сложности задач позволяет обеспечить значительный разрыв в их уровне и существенно усилить дифференцирующую возможность контроля.
Следующее требование, выполнение которого я считаю необходимым при разработке содержания контроля, состоит в том, что в целом контроль должен обеспечивать возможно большую полноту проверки на обязательном уровне. Именно полная информация об овладении обязательными результатами обучения дает возможность судить о готовности или неготовности ученика к продвижению по курсу, о выполнении или невыполнении им программных требований. В течение учебного года это поможет выявить затруднения учащихся, предупредить устойчивые пробелы в знаниях, в конце года позволит дать объективную оценку прочности знаний и умений школьников в соответствии с программными требованиями.
Важной частью работы предметника является умение вести мониторинговые исследования обязательного уровня усвоения тем учащимися. Так, в своей работе я придумала и использую мониторинг, который так и назвала, начинаю его использовать уже в 5 классе. Мониторинг №1 «Преемственность в 5 классе» (Приложение №2).
Мониторинг обязательного уровня усвоения содержания
обучения при переходе в 5 класс
| № п/п |  Тема Тема
| Нумерация | Арифметические действия | Величины | Геометрические фигуры |
| натуральные числа | названия и послед классов | читать, запис, срав числа | сумма разряд слагаемых | табл слож и умнож | порядок действий | связь между компон действ | свойства арифм действ | уравнения | единицы длины, пощади, массы, врем | связь м-ду: цена, кол-во, стоим | связь м-ду: скор, врем, растояние | периметр, дл отрезка, площ | действия с величинами | виды углов | виды треугольников | прямоуг-к квадрат | свойство стор прямоуг-ка | строить прям-к и отрезок |
| 1 | | | | | | | | | | | | | | | | | | | | |
| 2 | | | | | | | | | | | | | | | | | | | | |
| 3 | | | | | | | | | | | | | | | | | | | | |
В 2014 году учащиеся 9 класса, которых я обучала, успешно сдали ОГЭ по математике. Именно мониторинг помог мне постепенно в течение года вывести одного из учащихся на уровень, когда он преодолел порог успешности (приложение №4)
Библиографический список
Л. А. Александрова, Алгебра 7 класс. Самостоятельные работы. М.: Мнемозина 2009 г.
А. Г. Мордкович Алгебра . 7 класс. Учебник - М.: Мнемозина 2011 г.;
А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчинская Алгебра . 7 класс. Задачник – М: Мнемозина 2007 г.;
А. Г. Мордкович Алгебра 7-9 класс. Пособие для учителей М.: Мнемозина 2009 г.;
Настольная книга учителя математики М.: ООО «Издательство АСТ»:
ООО «Издательство Астрель» 2004 г.;
Зубарева И.И., Мордкович А.Г., «Математика, 6», 2005.
Зубарева И.И. Методическое пособие для учителя, 2003;
Самостоятельные работы в V-VI классах. // «Математика в школе», 2005. № 4, 6, 9, 19. 2006. № 1, 2;
Виленкин Н.Я. и др. «Математика», 6 класс. М.: «Мнемозина», 1998-2006. А. Г. Мордкович, Е. Е. Тульчинская Алгебра 7 класс. Контрольные работы - М.: Мнемозина 2009 г.
Тематическое приложение к вестнику образования № 4 2005 г.
Рецензия на целостное описания опыта
Иванушкиной Ирины Геннадьевны учителя математики МБОУ ООШ №7
муниципального образования Абинский район на тему «Мониторинг зачетов в системе дифференцированного обучения математике»
Важным элементом процесса обучения математике является контроль знаний и умений школьников. От того, как он организован, на что нацелен, существенно зависит эффективность учебной работы. Поэтому Ирина Геннадьевна на практике уделяет серьезное внимание способам организации контроля, его содержанию и мониторингу. Опыт работы Ирины Геннадьевны связан со стремлением более полно реализовать цели и задачи школьного математического образования. Содержание контроля выражено системой зачётов для всех классов с 5 по 11 (включая преемственность в 5 классе).
Учащиеся Ирины Геннадьевны получают право и возможность, обучаясь в одном классе и по одной программе, выбирать тот уровень усвоения, который соответствует их потребностям, интересам, способностям.
При создании системы зачётов учитель позволяет добровольно выбирать для себя уровень усвоения и отчетности в результатах своего учебного труда. Такой подход способствует психологическому комфорту ученика в школе, формирует у него чувство уважения к себе и к окружающим, вырабатывает ответственность и способность к принятию решений.
Ценность работы состоит в ее целостности, т. к. для каждого класса имеются система зачетов и механизм отслеживания результатов – мониторинг обязательного уровня усвоения учебного материала.
Зам директора по УВР Н.И. Еремеева
6
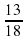 и
и 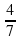
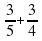 ; б)
; б) 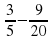
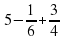 б)
б) 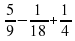
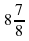 в виде неправильной дроби.
в виде неправильной дроби.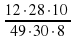 .
.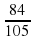 .
.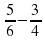 ; б)
; б) 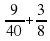
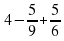 ; б)
; б) 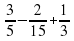
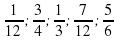
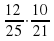 ; б)
; б) 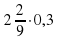 ; в)
; в) 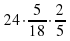 ;
; 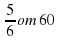 ; б) 0,7 от 40.
; б) 0,7 от 40.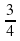 суток; за
суток; за 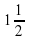 суток?
суток?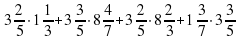
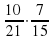 ; б)
; б) 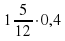 ; в)
; в) 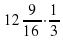 .
.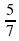 от 70; б) 0,6 от 50.
от 70; б) 0,6 от 50.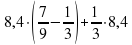
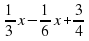 , при
, при 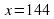 .
. 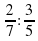 ; б)
; б) 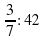 ; в)
; в) 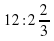 .
. ч. Зимой расход увеличился на 30%, а весной уменьшился па 50%. Как изменился расход электроэнергии?
ч. Зимой расход увеличился на 30%, а весной уменьшился па 50%. Как изменился расход электроэнергии?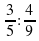 ; б)
; б) 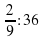 ; в)
; в) 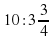 .
. 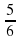 суток?
суток?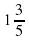 раза?
раза?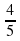 .
.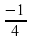 .
.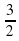 ; –7; 0;
; –7; 0; 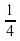 ; – 11; 6.
; – 11; 6.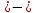 6; б) а2 при а= – 5.
6; б) а2 при а= – 5.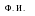 Тема
Тема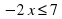 ; б)
; б) 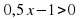 ; в)
; в) 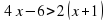 .
.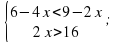 б)
б) 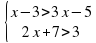 .
.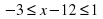
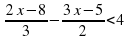 .
.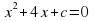 не имеет корней?
не имеет корней?















