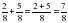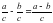Уроки математики позволяют сделать доступным для усвоения числовой материал краеведения. Решение задач, включающих данные краеведческого характера, способствует развитию творческого, логического, критического мышления и эрудиции; умению классифицировать и обобщать, расширяет кругозор. Материал для составления задач может быть получен не только из краеведческой литературы, но и самими учащимися при изучении объектов природы во время экскурсий. От учителя, его умения и мастерства подобрать примеры из окружающей действительности зависит качество усвоения материала детьми.
- Меню
- Главная
- Дошкольное образование
- Начальные классы
- Астрономия
- Биология
- География
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Естествознание
- Всемирная история
- Всеобщая история
- История России
- Право
- Окружающий мир
- Обществознание
- Экология
- Искусство
- Литература
- Музыка
- Технология (мальчики)
- Технология (девочки)
- Труд (технология)
- Физкультура
- ИЗО
- МХК
- ОБЗР (ОБЖ)
- Внеурочная работа
- ОРК
- Директору
- Завучу
- Классному руководителю
- Экономика
- Финансовая грамотность
- Психологу
- ОРКиСЭ
- Школьному библиотекарю
- Логопедия
- Коррекционная школа
- Всем учителям
- Прочее
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
- Главная
- Математика
- Прочее
- Методическая разработка на тему: «МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ КРАЕВЕДЧЕСКИХ МАТЕМАТИЧЕСКИХ ЗАДАЧ ПРИ ИЗУЧЕНИИ ДРОБЕЙ УЧАЩИМИСЯ 5-6 КЛАССОВ».
Методическая разработка на тему: «МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ КРАЕВЕДЧЕСКИХ МАТЕМАТИЧЕСКИХ ЗАДАЧ ПРИ ИЗУЧЕНИИ ДРОБЕЙ УЧАЩИМИСЯ 5-6 КЛАССОВ».
Просмотр содержимого документа
«Методическая разработка на тему: «МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ КРАЕВЕДЧЕСКИХ МАТЕМАТИЧЕСКИХ ЗАДАЧ ПРИ ИЗУЧЕНИИ ДРОБЕЙ УЧАЩИМИСЯ 5-6 КЛАССОВ».»
Государственное Бюджетное Профессиональное
Образовательное Учреждение
«Себряковский технологический техникум».
Методическая разработка на тему:
«МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ КРАЕВЕДЧЕСКИХ МАТЕМАТИЧЕСКИХ ЗАДАЧ ПРИ ИЗУЧЕНИИ ДРОБЕЙ УЧАЩИМИСЯ 5-6 КЛАССОВ».
Преподаватель математики:
Кузнецова А.И
г. Михайловка
2016 г.
Содержание
ВВЕДЕНИЕ…………………………………………………………………3-5
ГЛАВА 1. Теоретические основы использования краеведческих математических задач при изучении дробей
Элементы краеведения на уроках математики………………6-10
Понятие краеведческой задачи и этапы ее решения……………………………………………………………………….11-18
Выводы по 1 главе……………………………………………………….19
ГЛАВА 2. Практическая реализация методики формирования понятия дроби в 5-6 классах с использованием краеведческого материала
2.1. Введение понятия «обыкновенная дробь» с использованием краеведческого материала…………………………………………………..20-25
2.2. Введение понятия «десятичная дробь» с использованием краеведческого материала…………………………………………………26-29
2.3 Конспект урока по теме «Бородино»…………………………………………………………………30-43
Выводы по 2 главе ……………………………………………………..44-45
ЗАКЛЮЧЕНИЕ…………………………………………………………46
ЛИТЕРАТУРА………………………..……………………………........47
ВВЕДЕНИЕ
В последнее время в российском образовании заметно проявляется интерес к школьному краеведению, так как оно имеет большое значение для развития личности каждого ребенка. Краеведение является эффективным средством, способствующим формированию знаний учащихся, основанных на восприятии окружающего мира, развития и укрепления у детей чувства любви к родному краю; формирования нравственной личности гражданина и патриота России. Через краеведческую направленность происходит расширение и углубление содержания образования и воспитания школьников, границ их познавательной и исследовательской активности.
Трудно переоценить значимость для познавательного развития и воспитания человека изучения малой родины: ее природы, истории, культурных памятников, духовных ценностей, биографий достойных и уважаемых земляков. «Где родился, там и пригодился», - гласит пословица. Пригодиться своей родине может только тот человек, которого учили любить ее с детства и, конечно же, невозможно любить то, чего не знаешь.
Современный мир существенно раздвигает рамки образовательного процесса. Традиционный урок перестает быть для ребенка основным и единственным источником информации. Вместе с тем изучение родного края дает учителю надежный инструмент для реализации государственного образовательного стандарта. Краеведение позволяет успешно развивать, прежде всего, метапредметные умения. На близком и родном окружении доступно и понятно организовывать исследовательскую и проектную деятельность, видеть свои проектные преобразования.
Метапредметная интеграция – проявляется в интегрировании краеведческого материала в различные темы предметов; спровоцированное (созданное) учителем состояние интеллектуального затруднения ученика, когда он обнаруживает, что для решения поставленной перед ним задачи ему недостаточно имеющихся предметных знаний и умений.
Интегрированные уроки математики и краеведения особенно актуальны, поскольку обладают ярко выраженной прикладной направленностью и вызывают неизменный познавательный интерес у обучающихся. При интеграции этих уроков происходит использование потенциала нескольких учебных дисциплин, открываются дополнительные возможности для решения учебных и воспитательных задач, уплотнение количества информации на уроке и мыслительной деятельности учеников по усвоению этой информации. На интегрированных уроках здание математики создаётся на глазах детей и с их посильным участием, отчётливо выявляются связи математических понятий с практической деятельностью человека. Эмоциональный настрой учителя, неординарность ситуации на интегрированном уроке передаётся обучающимся.
Уроки математики позволяют сделать доступным для усвоения числовой материал краеведения. Решение задач, включающих данные краеведческого характера, способствует развитию творческого, логического, критического мышления и эрудиции; умению классифицировать и обобщать, расширяет кругозор. Материал для составления задач может быть получен не только из краеведческой литературы, но и самими учащимися при изучении объектов природы во время экскурсий. От учителя, его умения и мастерства подобрать примеры из окружающей действительности зависит качество усвоения материала детьми. Примеров много: это задачи-расчеты, информация о животном и растительном мире, протяженность территориальных границ, площади территорий, протяженность рек местного характера и т.п. – вот неполный перечень краеведческого материала для составления текстов задач.
Таким образом, целью курсовой работы является обоснование возможности и целесообразности использования краеведческого материала в математике при изучении дробей школьниками 5-6 классов.
Чтобы достичь цели, нам потребуется решить следующие задачи:
Выявить сущность понятий «краеведение» и «краеведческая деятельность» на уроках математики.
Выявить содержание понятия «краеведческая задача» и этапы ее решения.
Выявить методические особенности использования краеведческого материала при изучении дробей в 5-6 классах.
Разработать уроки по использованию краеведческих задач при изучении дробей в 5-6 классах.
Объект исследования – процесс изучения дробей в 5-6 классах
Предмет исследования – методические особенности использования краеведческих задач при изучении дробей в 5-6 классах.
Обратимся к материалам исследования.
Глава 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИСПОЛЬЗОВАНИЯ КРАЕВЕДЧЕСКИХ МАТЕМАТИЧЕСКИХ ЗАДАЧ ПРИ ИЗУЧЕНИИ ДРОБЕЙ
1.1 ЭЛЕМЕНТЫ КРАЕВЕДЕНИЯ НА УРОКАХ МАТЕМАТИКИ
В настоящее время краеведение стало очень острой и актуальной темой в образовании. В век высоких технологий теряется нить, которая связывает нас с прошлым, настоящим и будущим. Современный человек должен восстановить и сохранить ту хрупкую нить, что и предполагает краеведение. Использование краеведческого материала на уроках несет очень большой объем знаний по различной тематике: география, животный мир, растительный мир, история, литература, фольклор.
Краеведение в школе и его интеграция с другими предметами – ключ к решению проблемы эффективности урока, на таком уроке легко соединяются три важных в образований цели – это обучающая, развивающая и воспитательная цель. Межпредметная интеграция с использованием краеведческого материала активизирует мыслительную деятельность, вызывает большой интерес к истории города, села; происхождению фамилий, имени, названию, городов, сел, рек. Использование такого материала делает урок интересным, увлекательным, что повышает эффективность урока. Известно, что дети охотнее и с большим интересом усваивают то, что им больше нравится. Любимые предметы имеют сильное воспитательное воздействие, поэтому грамотное использование исторического, географического и другого материала воспитывает в детях патриотические чувства: любви, восхищения и гордости к родному краю, что не оставляет никого быть равнодушным к проблемам малой родины и вырабатывает активную жизненную позицию.
Работая над краеведческим материалом и используя его на уроках важно придерживаться определенных принципов:
систематичность;
доступность;
наглядность;
разнообразность материала;
связь материала в учебной и воспитательной работе;
взаимосвязь местного и общего исторического, географического и литературного материала
Важно, чтобы на таких уроках широко использовалась наглядность – это могут быть иллюстрации, фотографии, презентации, слайд-фильмы. При разработке упражнений по математике необходимо подбирать материал, который будет интересен и понятен детям и подкреплён наглядностью.
Воспитывающее воздействие данных, приводимых в «текстовых» задачах, хотя и должно, конечно, всемерно быть использовано, но с математическим содержанием урока связано лишь внешним образом; ясно, что здесь воспитывающее влияние призвана оказывать не сама математика, не ее законы и ее стиль, а те привязанные к ней чисто внешним образом данные, которые обрамляют собою «текстовые» задачи и которые без всякого изменения математического содержания задачи могли бы быть заменены любыми другими аналогичными данными.
Ознакомление с математическими фактами, разбор и усвоение математических теорем, выведение формул, решение значительного количества упражнений развивают способности человека и оказывают известное влияние на развитие математического мышления учащихся.
Однако только этими средствами задача математического развития и воспитания в той мере, в какой это требуется в современных условиях, не может быть обеспечена.
Любая задача, которая ставится на том или ином этапе обучения, несет в себе разные функции, причем ведущее положение одной или нескольких функций задачи имеет динамичный характер. В связи с этим существует возможность усиления одной или нескольких функций задач (без ослабления остальных функций). В частности, можно усилить развивающие или воспитывающие функции многих задач, имеющих сугубо обучающий характер. Этого можно достичь различными путями – частичным изменением условия данной задачи, рассмотрением ее частных или предельных случаев и т.д. Существенно усилить воспитывающие функции задач может решение специально подобранных нестандартных задач. Такие задачи помогают погрузиться в прошлое, реально представить его картины и вместе с тем как бы стать участником былых событий.
Интеграция элементов краеведения на уроках математики требует активных форм и методов обучения:
уроки-путешествия;
экскурсии и наблюдения;
конкурсы и викторины;
задания на краеведческой основе.
Решение сюжетных задач, включающих исторические сведения, способствует развитию кругозора учащихся и познавательного интереса к предмету. И урок математики становится для них не просто уроком, на котором нужно решать, вычислять и заучивать формулы, а пробуждает чувства сопричастности с величием собственных предков.
Одно из плодотворных направлений модернизации краеведческого образования – проектная деятельность школьников, которая развивает у детей самостоятельность, творческое отношение к делу, способствует формированию навыков поисково-исследовательской деятельности, созданию условий для подготовки к продолжению образования.
Прежде чем составить такую задачу с использованием краеведческого материала,
1) учащийся должен собрать необходимые сведения при посещении экскурсий (делая пометки в блокнот) или самостоятельно (посещая библиотеки, с помощью Интернета)
2) проанализировать, подходят ли полученные данные для составления задач, заданий, уравнений, примеров по определенной теме.
Работа такого характера формирует следующие мыслительные операции: анализ, синтез, сравнение; развивает познавательную активность, самостоятельность учащихся.
Таким образом, элементы краеведения на уроках математики положительно влияют на результативность знаний учащихся, на развитие их как личности, носят воспитывающий характер.
Решение задач с использованием краеведческого материала
1. позволяет углубить знания учащихся по краеведению;
2. способствует привитию интереса к математике;
3. развитие творческое мышление, творческий потенциал учащихся и познавательной активности;
4. формирует ответственный подход к решению задач, обогащает общую культуру учащихся;
5. формируются такие качества, как самостоятельность, ответственность, любовь к родному краю, своей малой родине.
Схема краеведение в математике.
Математика позволяет сделать доступным для усвоения числовой материал краеведения. Решение задач, включающих данные краеведческого характера, способствует развитию творческого, логического, критического мышления, эрудиции, умению классифицировать и обобщать, расширяет кругозор. Тот, кто хоть раз испытал радостное чувство от решения трудной задачи, познал радость пусть маленького, но открытия (а каждая задача в математике – это проблема, к решению которой человечество шло порою долгие годы), будет стремиться познавать всё больше и использовать полученные знания в жизни. Таким образом, краеведение является эффективным средством, способствующим формированию знаний учащихся, в том числе и математических.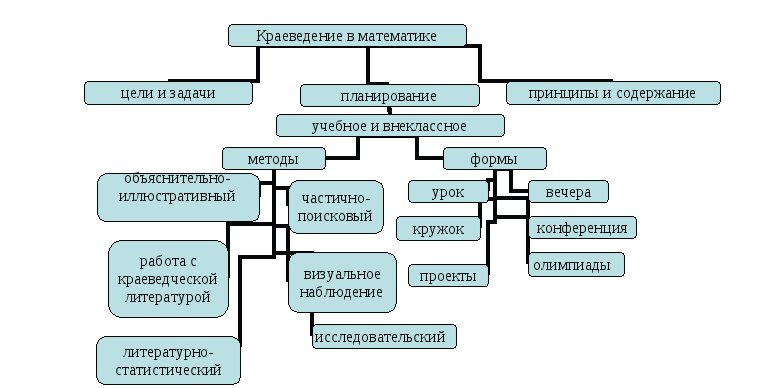
Многие утверждают, что математика - это сухие цифры, формулы и непонятные уравнения. Можно поспорить с этим утверждением. Урок нестандартный, в том числе интегрированный, не только обеспечивает успешное овладение таким сложным предметом, как математика, но и развивает личность школьника, его интеллектуальные и творческие способности и, что особенно немаловажно, - его ценностные ориентации: любовь к родине, родному краю, уважение к его истории, духовным и культурным ценностям.
1.2 Понятие краеведческой задачи и этапы ее решения.
Решение сюжетных задач является для учащихся традиционно затруднительным. Увидев текстовую сюжетную задачу в контрольно-измерительных материалах, многие даже не приступают к её решению. Однако, решение сюжетных задач связано с моделированием, которое позволяет ученику повысить свой уровень изучения математики до уровня владения математическими законами. Поэтому остается актуальной проблема использования текстовых сюжетных задач как средства обучения учащихся математике.
Использование задач с краеведческим материалом позволит заинтересовать учащихся, привлечет их внимание хотя бы для прочтения сюжета, однако для того, чтобы узнать ответ задачи ее необходимо решить, поэтому сюжет может повлиять на мотивацию учащихся на решение задач.
Математические задачи краеведческого характера - задачи, содержащие сведения из истории родного края, памятных местах, традициях, выдающихся земляках. Как средство обучения учащихся решению текстовых сюжетные задачи могут использоваться с двух сторон. С одной стороны, на уроках математики решаются предложенные задачи с историко-краеведческой фабулой. С другой стороны, сюжетные задачи конструируются самими учащимися на ими отобранном историческом материале. Важным условием в этом случае является реальность используемой информации, достоверность фактов.
Основная идея обучения решению сюжетных задач заключается в обучении учащихся конструированию таких задач. Синтез как логический прием мышления сформировать сложнее, однако удается в большей степени при конструировании учащимися сюжетных задач. Сюжет задачи учащиеся должны отыскать в краеведческих материалах своей местности (например, история города, история битвы). Затем на числовых данных построить всевозможные зависимости, сконструировать математическую задачу. Такая работа способствует не только обучению математике, но и сохранению исторической памяти учащихся.
Общий прием решения краеведческих задач включает: знание этапов решения, методов (способов) решения, типов задач, обоснование выбора способа решения на основании анализа текста задачи, а также владение предметными знаниями: понятиями, определениями терминов, правилами, формулами, логическими приемами и операциями.
К этапам решения можно отнести:
1) анализ текста задачи;
2) перевод текста на язык математики;
3) установление отношений между данными и вопросом;
4) составление плана решения задачи;
5) осуществление плана решения;
6) проверка и оценка решения задачи.
Анализ текста краеведческой задачи.
Работа над текстом краеведческой задачи включает семантический, краеведческий, логический и математический анализ.
1. Семантический анализ направлен на обеспечение понимания содержания текста и предполагает:
выделение и осмысление:
отдельных слов, терминов, понятий, как житейских, так и математических,
грамматических конструкций ("если… то", "после того, как…" и т.д.),
количественных характеристик объекта, задаваемых словами "каждого", "какого-нибудь", "любое", "некоторое", "всего", "все", "почти все", "одинаковые", "столько же", "поровну" и т.д.;
восстановление предметной ситуации, описанной в задаче, путем упрощенного пересказа текста с выделением только существенной для решения задач информации;
выделение обобщенного смысла задачи - о чем говорится в задаче, указание на объект и величину, которая должна быть найдена (стоимость, объем, площадь, количество и т.д.)
2. Логический анализ предполагает:
умение заменять термины их определениями;
выводить следствия из имеющихся в условии задачи данных (понятия, процессы, явления).
3. Математический анализ включает анализ условия и требования задачи.
Анализ условия направлен на выделение:
а) объектов (предметов, процессов);
б) величин, характеризующих каждый объект;
в) характеристик величин (числовые значения, известные и неизвестные данные, отношения между известными данными величин).
Анализ требования направлен на выделение:
неизвестных количественных характеристик величин объектов или объекта.
Краеведческий анализ включает в себя информацию выбранного края, города, страны.
Перевод текста на язык математики.
В результате анализа краеведческой задачи текст задачи записывают кратко с использованием условной символики. После того как данные задачи специально вычленены в краткой записи, следует перейти к анализу отношений и связей между этими данными.
Для этого осуществляется перевод текста на язык графических моделей различного вида: чертеж, схема, график, таблица, символический рисунок, формула, уравнение и др. Перевод текста в форму модели позволяет обнаружить в нем свойства и отношения, которые часто трудно выявить при чтении текста.
Выполненный чертеж (рисунок) по тексту задачи позволяет фиксировать ход рассуждений при ее решении, что способствует формированию общих подходов к решению задач.
Поэтому к выполнению чертежей нужно предъявлять требования: они должны быть наглядными, четкими, соответствовать тексту задачи; на них должны быть отражены по возможности все данные, входящие в условие задачи; выделенные на них данные и искомые должны соответствовать условию задачи и общепринятым обозначениям.
Формирование умения выполнять чертеж задачи будет успешным, если учащиеся будут уметь читать соответствующий чертеж.
В связи с этим учащимся нужно предлагать упражнения на составление текста задачи по чертежу, рисунку.
Установление отношений между данными и вопросом.
Реализация этого компонента общего приема решения задач предусматривает установление отношений между:
данными условия,
данными вопроса,
данными условия и вопросом задачи.
На основе анализа условия и вопроса краеведческой задачи определяется способ решения задачи (вычислить, построить, доказать), выстраивается последовательность конкретных действий.
При этом устанавливается достаточность, недостаточность или избыточность данных.
Выделяются четыре типа отношений между объектами и их величинами: равенство, часть/целое, разность, кратность, сочетание которых определяет разнообразие способов решения задач.
Примером такого отношения является формула а b=c, имеющая большое число разнообразных проявлений (связь пройденного пути, времени и скорости равномерного движения; связь цены, стоимости и количества изделий и т.д.).
План решения.
На основании выявленных отношений между величинами объектов выстраивается последовательность действий - план решения. Особое значение имеет составление плана решения для сложных, составных задач.
Осуществление плана решения включает:
решение задачи - выполнение действий;
запись решения задачи;
выделение способов решения.
Запись решения задачи может осуществляться в виде записи последовательных определенных действий (с пояснениями и без) и в виде выражения (развернутого или сокращенного).
Проверка и оценка решения краеведческой задачи с точки зрения адекватности плана решения, способа решения, ведущего к результату: рациональность способа, нет ли более простого.
Различные типы задач требуют использования разных методов и приемов решения. Решение краеведческих задач в 5-6 классах осуществляется в основном тремя способами:
арифметическим, состоящим в нахождении значений неизвестной величины посредством составления числового выражения (числовой формулы) и подсчета результата;
алгебраическим, при котором составляется уравнение (система уравнений), решение которого основано на свойствах уравнений;
комбинированным, который включает как арифметический, так и алгебраический способы решения.
Арифметические способы решения краеведческих задач позволяют развивать умение анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами (с учетом типа задачи), истолковывать результат каждого действия в рамках условия задачи, проверять правильность решения с помощью составления и решения обратной задачи, то есть формировать и развивать важные общеучебные умения.
Арифметические способы решения краеведческих задач приучают детей к первым абстракциям, позволяют воспитывать логическую структуру, могут способствовать созданию благоприятного эмоционального фона обучения, развитию у школьников эстетического чувства применительно к решению задачи (красивое решение) и изучению математики, вызывая интерес сначала к процессу поиска решения задачи, а потом и к изучаемому предмету [3].
При решении арифметическим способом формы записи могут быть:
вопрос с последующим действием;
действие с последующим объяснением;
запись решения с предшествующим пояснением;
числовое решение без всякого текста.
При решении краеведческой задачи алгебраическим способом существенное значение имеет выбор величины за неизвестное, с помощью которого можно выразить остальные (или часть остальных) величины, входящие в задачу, и установить зависимость между данными задачи, которая даст возможность составить уравнение.
Для многих задач за неизвестное можно принимать величину, которую требуется найти; тогда ответ на вопрос задачи получается без дополнительных вычислений.
При решении краеведческой задачи часто используют сочетание арифметического и алгебраического способов решения. В силу этого форма записи решения каждой части будет разной.
Все краеведческие задачи школьного курса математики 5-6 классов можно сгруппировать следующим образом:
задачи по теме "Натуральные числа" (краеведческие задачи на все действия с натуральными числами);
задачи по теме "Рациональные числа" (краеведческие задачи на все действия с рациональными числами, на нахождение дроби от числа, на нахождение числа по дроби, задачи на совместную работу, задачи на проценты);
задачи на движение;
задачи на прямую и обратную пропорциональную зависимость;
задачи на составление уравнений;
задачи на смеси и сплавы.
При решении краеведческих задач в курсе математики 5-6 классов очень важно соблюдать преемственность преподавания.
Учитель математики должен познакомиться с методикой преподавания учителя начальных классов, знать основные приемы работы этого учителя и продолжать применять их, не сильно отступая от того, чему дети уже научены (составление схем, таблиц, краткой записи условия задачи и т.д.), дополняя, обогащая способы решения задач своими наработками.
Ученики начальной школы все краеведческие задачи делят на задачи:
в одно действие;
в два действия;
в три действия.
Поэтому чаще всего (особенно слабые) решают задачи перебором действий (какое подойдет).
В 5 классе приходится не сильно отступая от начальной школы исправлять и уделять много внимания решению задач на нахождение отношений между числами ("больше на…", "меньше на…", "больше в … раз", "меньше в …раз").
Дети справляются с заданием легко, но далеко не все правильно. А проверяют они по рисунку, который показывает учитель. Задания подобного рода нужно давать продолжительное время, пока не исчезнут ошибки, но они не обязательны для всех.
Также очень важно детей учить делать прикидку ответа задачи.
Составление краткой записи условия задачи, схем, рисунков и т.д. учащиеся должны сопровождать объяснением и обсуждением в парах, у доски, индивидуально учителю, но ни в коем случае не молча. Проговаривая каждый свой шаг учащиеся лучше осознают условие задачи и находят в нем все больше и больше знакомых им известных ситуаций, особенно, если эта задача состоит из нескольких элементарных задач.
Помогает в решении краеведческих задачи расчленение ее на более мелкие ситуации. Ученику лучше предлагать вспомогательную ситуацию из его жизни, интересную и понятную. Например, в магазин пошли не кто-то другой, а ты и твой друг или ты догоняешь на велосипеде своего друга и другие.
Никогда не нужно торопить ребенка с решением, если у него возникают трудности. Нужно попытаться помочь ему еще и еще раз. Обязательно похвалить за решенную задачу, даже если он сам в ней верно сделал только один шаг. В таком случае он на следующем уроке будет вдвойне внимателен и сделает верно уже не один шаг, а больше. И может решить ее всю. Для детей, у которых задачи не получаются, учитель должен становиться помощником, другом, соучастником решения проблемы. Нужно заставить ребенка преодолеть страх перед задачами. Он у них вырабатывается в начальной школе, так как содержание задач не всегда соответствует возрасту.
При решении задач по теме "Натуральные числа" дети опираются на знания, полученные в начальной школе, и при правильно построенной методике преподавания в 5-6 классе с краеведческими задачами справляются.
Задачи "на проценты", "на дроби" можно изучать в комплексе:
вместе все три вида задач на проценты;
вместе нахождение дроби от числа и числа по дроби.
Дети учатся находить отличие в формулировке задач, в данных задачи, в вопросе.
В решении также помогает правильно составленная по условию задачи схема, прикидка ответа и соответствие полученного ответа условию задачи. Нужно добиваться, чтобы дети при решении не пропускали ни одного из этих шагов. Тогда успех обеспечен.
Выводы по 1 главе
Таким образом, в первой главе было проанализировано значение краеведения и краеведческих задач в математике 5-6 классов, что позволило сделать вывод о том, что элементы краеведения на уроках математики положительно влияют на результативность знаний учащихся, на развитие их как личности, носят воспитательный характер. Решение таких задач способствует расширению кругозора, связывает математику с окружающей действительностью.
Объектами краеведения являются природа, историческое прошлое, искусство, культура. Все это объекты разных наук, и, следовательно, при их изучении используются разные методы, присущие соответствующим областям знания.
Краеведение в школе играет существенную педагогическую роль в трудовом, нравственном и эстетическом воспитании учащихся, занимает важное место в формировании патриотизма молодого поколения, т. к. «свои истоки любовь к Родине берет в стране нашего детства – отчем крае, чей светлый образ навсегда остается в сердце каждого»
Математические задачи краеведческого характера - задачи, содержащие сведения из истории родного края, памятных местах, традициях, выдающихся земляках. Функции краеведческих задач как цели обучения.
Этапам решения краеведческих задач:
1) анализ текста задачи;
2) перевод текста на язык математики;
3) установление отношений между данными и вопросом;
4) составление плана решения задачи;
5) осуществление плана решения;
6) проверка и оценка решения задачи.
ГЛАВА 2. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ МЕТОДИКИ ФОРМИРОВАНИЯ ПОНЯТИЯ ДРОБИ В 5-6 КЛАССАХ С ИСПОЛЬЗОВАНИЕМ КРАЕВЕДЧЕСКОГО МАТЕРИАЛА
2.1. Введение понятия «обыкновенная дробь» с использованием краеведческого материала
Пусть требуется измерить длину отрезка х с помощью единичного отрезка е. При измерении оказалось, что отрезок х состоит из трех отрезков, е, и отрезка, который короче отрезка е. В этом случае длина отрезка х не может быть выражена натуральным числом. Однако, если отрезок е разбить на 4 части, то отрезок х окажется состоящим из 14 отрезков, равных четвертой части отрезка е. И тогда, говоря о длине отрезка х, мы должны указать два числа 4 и 14: четвертая часть отрезка е укладывается в отрезке точно 14 раз. Поэтому условились длину отрезка х записывать в виде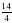 Е, где Е – длина единичного отрезка е, а символ
Е, где Е – длина единичного отрезка е, а символ 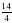 называют дробью.
называют дробью.
В общем виде понятие дроби определяют так. Пусть даны отрезок х и единичный отрезок е, длина которого Е. Если отрезок х состоит из m отрезков, равных n-ой части отрезка е, то длина отрезка х может быть представлена в виде 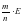 , где символ
, где символ 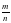 называют дробью.
называют дробью.
К записи дроби 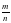 числа m и n – натуральные, m – называется числителем, n – знаменателем дроби.
числа m и n – натуральные, m – называется числителем, n – знаменателем дроби.
Дробь 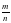 называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.
называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.
Вернемся к тому, что четвертая часть отрезка е уложилась в отрезке х точно 14 раз. Очевидно, это не единственный вариант выбора такой части отрезка е, которая укладывается в отрезке х целое число раз. Можно взять восьмую часть отрезка е, тогда отрезок х будет состоять из 28 таких частей и длина его будет выражаться дробью 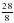 . Можно взять шестнадцатую часть отрезка е, тогда отрезок х будет состоять из 56 таких частей и его длина будет выражаться дробью
. Можно взять шестнадцатую часть отрезка е, тогда отрезок х будет состоять из 56 таких частей и его длина будет выражаться дробью 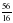 .
.
Вообще длина одного и того же отрезка х при заданном единичном отрезке е может выражаться различными дробями, причем, если длина выражена дробью 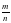 , то она может быть выражена и любой дробью вида
, то она может быть выражена и любой дробью вида 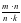 , где к – натуральное число.
, где к – натуральное число.
Теорема. Для того чтобы дроби 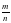 и
и 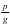 выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство mg = np
выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство mg = np
Определение: Две дроби 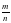 и
и 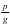 называются равными, если mg = np. Если дроби равны, то пишут
называются равными, если mg = np. Если дроби равны, то пишут 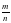 =
=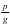 .
.
Например 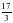 =
=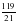 , так как 17 х 21 = 119 х 3 = 357, а
, так как 17 х 21 = 119 х 3 = 357, а 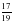 ≠
≠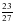 , потому что 17 х 27 = 459,19 х 23 = 437 и 459 ≠ 437.
, потому что 17 х 27 = 459,19 х 23 = 437 и 459 ≠ 437.
Из сформулированных выше теоремы и определения следует, что две дроби равны тогда и только тогда, когда они выражают длину и того же отрезка.
Нам известно, что отношение равенства дробей рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности. Теперь, используя определение равных дробей, это можно доказать.
Теорема. Равенство дробей является отношением эквивалентности.
Доказательство: Действительно, равенство дробей рефлексивно: 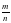 =
= 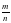 , так как равенство mn = mn справедливо для любых натуральных числе m и n.
, так как равенство mn = mn справедливо для любых натуральных числе m и n.
Равенство дробей симметрично: 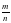 =
=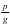 , то
, то 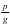 =
=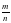 , так как из mg = np следует, что pn = mg (m,n,p,g ε N).
, так как из mg = np следует, что pn = mg (m,n,p,g ε N).
Оно транзитивно: если 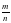 =
= 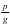 и
и 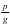 =
=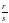 , то
, то 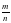 =
= 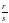 .
.
В самом деле, так как 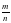 =
= 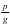 , то mg = np, так как
, то mg = np, так как 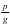 =
= 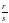 , то ps = gr. Умножив обе части равенства mg = np на s, а равенство ps = gr на n, получим mgs = nps и nps = grs. Откуда mgs = grs или ms = nr. Последнее равенство означает, что
, то ps = gr. Умножив обе части равенства mg = np на s, а равенство ps = gr на n, получим mgs = nps и nps = grs. Откуда mgs = grs или ms = nr. Последнее равенство означает, что 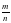 =
= 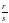 . Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно оно является отношением эквивалентности.
. Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно оно является отношением эквивалентности.
Из определения равных дробей вытекает основное свойство дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
На этом свойстве основанного сокращение дробей и приведение дробей к общему знаменателю.
Сокращение дробей – это замена данной дроби другой, равной данной, но с лишим числителем и знаменателем.
Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называют несократимой. Например, 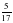 - несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу, т.е. В (5; 17) = 1.
- несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу, т.е. В (5; 17) = 1.
Приведение дробей к общему знаменателю – это замена данных дробей, равными им дробями, имеющими одинаковые знаменатели. Общим знаменателем двух дробей 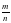 =
= 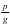 является общее кратное чисел n и g, а наименьшим общим знаменателем – их наименьшее.
является общее кратное чисел n и g, а наименьшим общим знаменателем – их наименьшее.
Сравнения обыкновенных дробей с одинаковыми знаменателями.
Чтобы сравнить две обыкновенные дроби с одинаковыми знаменателями, нужно сравнить их числители: больше та дробь, у которой больше числитель.
Задание: На полях Волгоградской области в 2003 году засеяли 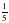 картофеля и
картофеля и 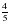 пшеницы. Сравните дроби и скажите, чего засеяли больше.
пшеницы. Сравните дроби и скажите, чего засеяли больше.
|
|
| Сравнение дробей с одинаковыми числителями.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Сравнение дробей с разными знаменателями.
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями. |
Операции сложение и вычитание дробей с одинаковыми знаменателями.
При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
С помощью букв правило сложения можно записать так: 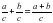
Задание:
| Яблочный сад во Фролова разделили на 8 равных частей (долей). Сначала на 2 доли, а потом еще 5 долей. Оказалось 7 долей, то есть При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же: |
Сложение и вычитание дробей с разными знаменателями.
Чтобы сложить (вычесть) дроби с разными знаменателями нужно воспользоваться следующими правилами.
Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти наименьшее общее кратное знаменателей.
Задание: Поле засеяли гречкой 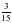 в первую неделю, а во вторую неделю засеяли
в первую неделю, а во вторую неделю засеяли 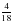 . Сколько всего засеяли?
. Сколько всего засеяли?
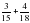
Как найти общий знаменатель?
Находим НОК (15, 18).
нахождение общего знаменателя НОК (15, 18) = 3 • 2 • 3 • 5 = 90
Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1) делим по очереди на знаменатель каждой дроби. Полученные числа и будут дополнительными множителями для каждой из дробей. Множители записываем над числителем дроби справа сверху.
90 : 15 = 6 - дополнительный множитель для дроби 3/15.
90 : 18 = 5 - дополнительный множитель для дроби 4/18.
Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь основным свойством дроби. После умножения в знаменателях обеих дробей должен получиться наименьший общий знаменатель. Затем складываем дроби как дроби с одинаковыми знаменателями.
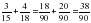
Проверяем полученную дробь.
Eсли в результате получилась неправильная дробь, результат записываем в виде смешанного числа. Проверим нашу дробь 38
Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
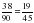
Операция умножения дробей.
Произведение дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель произведению их знаменателей: 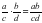
Задание:
Выполните умножение дробей 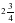 и
и 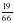 . Числитель полученной дроби подскажет, в каком году была открыта 35 школа города Серафимович.
. Числитель полученной дроби подскажет, в каком году была открыта 35 школа города Серафимович.
Операция деления дробей.
Частное от деления дроби на дробь равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель равен произведению знаменателя первой дроби на числитель второй дроби: 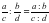
Задание:
Дорога от села Себровка до села Новостройка длиной 20 м, ее разделили на 3 товарных пункта. Какова длина одной части дороги от одного до другого пункта?
2.2. Введение понятия «десятичная дробь» с использованием краеведческого материала
Явно неудачно определение десятичной дроби как особой формы записи дроби со знаменателем вида 10n. Во-первых, этому определению не соответствуют бесконечные дроби (периодические и непериодические).
Во-вторых, если бы десятичная дробь была дробью, то все теоремы о дробях относились бы и к десятичным дробям (как относятся они, например, ко всем правильным дробям). Но это не так. Во всех теоремах о дробях (например, в теореме об основном свойстве дроби) говорится о числителе, знаменателе и черте дроби. А десятичная дробь не имеет ни числителя, ни знаменателя, ни этой черты. Зато она имеет важный элемент (запятую), которого не имеет дробь. Значит, десятичная дробь не является дробью.
В таком словоупотреблении нет ничего особенного. Не только в математическом, но и в обычном языке конструкция «существительное + прилагательное» может определять нечто отличное от этого существительного, взятого отдельно. Например, морская свинка вовсе не свинка. Родовым понятием для десятичной дроби нужно считать не «дробь», а «десятичное число» (число, записанное в десятичной системе счисления).
Определение. Десятичной дробью называется десятичное число (число, записанное в десятичной системе счисления), имеющее цифры в разрядах правее (меньше) разряда единиц. Эти разряды отделяются от разряда единиц запятой. Число, стоящее в десятичной дроби левее запятой, называется целой частью десятичной дроби. Число, стоящее в десятичной дроби правее запятой, называется дробной частью десятичной дроби. Цифры, стоящие в дробной части десятичной дроби, называются десятичными знаками. Такое определение десятичных дробей дает возможность изучать их до обыкновенных дробей. Но даже если обыкновенные дроби изучаются до десятичных, данное определение ничем не мешает, а только помогает использовать при изучении десятичных дробей известные ученикам алгоритмы работы с многозначными числами (действия «столбиком» и «уголком»).
Задание на распознавание:
Среди чисел 0,78; 10; 921; 23; 23,0 найдите, которые являются десятичными дробями, и те, которые не являются ими. Назовите целую часть и дробную часть каждой найденной десятичной дроби и все ее десятичные знаки. (При выполнении задания число 23,0 должно быть признано десятичной дробью, а число 23 нет.)
Cравнение десятичных дробей.
Чтобы сравнить две десятичные дроби, нужно сравнить их целые части: больше то число, у которого больше целая часть; если целые части равны, то нужно сравнивать цифры в разряде десятых, сотых и т.д. до обнаружения неравных цифр. Та дробь больше, которая содержит эту большую цифру. Каждая десятичная дробь, имеющая ненулевые десятичные знаки, больше натурального числа, равного целой части этой десятичной дроби, но меньше этого натурального числа, увеличенного на единицу.
Задание:
Тогда расставьте дроби в порядке возрастания, каждой дроби соответствует буква.
3,567; 3,067; 3,105; 3,0005; 3,9; 3,14; 3,1052; 3,002; 3,899
| 3,0005 | 3,002 | 3,067 | 3,105 | 3,1052 | 3,14 | 3,567 | 3,899 | 3,9 |
| В | о | л | г | о | г | р | а | д |
|
|
|
|
|
|
|
|
|
|
Сложение и вычитание десятичных дробей.
Десятичные дроби складываются и вычитаются между собой и с натуральными числами по разрядам. При сложении и вычитании десятичных дробей столбиком они подписываются запятая под запятой.
Задание:
Вычисли. Зашифрованное слово – один из памятников Волгограда.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7,5 |
16,8 |
8,98 |
1,9 |
9,1 |
0,6 |
32,6 |
323,1 |
7,92 |
1,62 |
3,4 |
63,5 |
Д. 5,9 + 1,6 У. 6,35 · 10
Ж. 8,3 + 0,8 Е. 5,7 + 3,28
Р. 4,7 – 2,8 Н. 45,6 – 13
З. 12,1 + 4,7 И. 3 – 2,4
М. 12,1 – 8,7 С. 5,2+ 317,9
К. 17,15 – 9,23 О. 16,2 : 10
Алгоритм умножения.
Чтобы перемножить две десятичные дроби
или десятичную дробь и натуральное число, нужно выполнить умножение, не обращая внимания на запятые, а затем в произведении отделить запятой справа столько десятичных знаков, сколько их всего в обоих множителях.
Задание:
Из городов Волгоград и Михайловка одновременно навстречу друг другу выехали два автобуса. Один двигался со скоростью 2,6 км/ч, а другой со скоростью 1,3 км/ч. Какое расстояние они проехали вместе, если встретились через 2,1ч?
Способ1
1) 2,6 * 2,1=5,46(км)прошёл первый человек
2) 1,3 * 2,1=2,73 (км) прошёл второй человек
3) 5,46+2,73=8,19 (км) весь путь
Ответ: 8,19км
Способ 2
1) 2,6+1,3=3,9 (км/ч) скорость сближения
2) 3,9 * 2,1=8,19 (км) весь путь
Ответ: 8,19км
Алгоритм деления десятичной дроби на натуральное число.
Выполняя деление десятичной дроби на натуральное число, нужно разделить на него целую часть делимого; когда заканчивается деление целой части (сносится цифра десятых), в частном ставится запятая и деление продолжается.
Задание:
Сколько километров мы пройдем по лесу города Фролово за 0,5 ч, если будем идти со скоростью 4,5 км/ч?
Решение:
За 1ч – 4,5 км, тогда за 0,5 ч = 1/2 ч
4,5 : 2 = 2,25 (км).
Ответ: 2,25 км.
Сколько километров мы будем идти до леса города Фролово, если скорость будет та же, 4,5 км/ч, а идти мы будем 1,5 ч?
Решение:
1,5 ч = 1 ч + 0,5 ч, значит, мы пройдем 4,5 км + 2,25 км = 6,75 км.
Ответ: 6,75 км.
Слайд 5. Задача 3
Сколько всего километров нам надо будет пройти?
Решение :
6,75 км + 2,25 км = 9 км.
Ответ: 9 км.
Алгоритм деления на десятичную дробь.
Чтобы выполнить деление на десятичную дробь, нужно:
1) заменить делитель на натуральное число и выяснить, во сколько раз он от этого увеличился;
2) увеличить во столько же раз делимое;
3) выполнить деление полученных чисел.
2.3 Конспект урока по теме «Бородино»
Решение задач, включающих данные краеведческого характера, способствует развитию творческого, логического, критического мышления и эрудиции; умению классифицировать и обобщать, расширяет кругозор. На мой взгляд, самой распространенной формой реализации применения краеведческого материала на уроках математики являются задачи и математические диктанты.
Материал для составления задач может быть получен не только из краеведческой литературы, но и самими учащимися при изучении объектов природы во время экскурсий. От учителя, его умения и мастерства подобрать примеры из окружающей действительности зависит качество усвоения материала обучающимися. Примеров много: это задачи-расчеты, информация о животном и растительном мире, протяженность территориальных границ, площади территорий, протяженность местных рек и т.п. Приведу пример – конспект урока.
Конспект урока. Урок математики с элементами краеведения по теме: «Бородино».
Цели урока.
Образовательный аспект:
в ходе совместной, индивидуальной работы:
- повторить и углубить знания по теме «Бородино»;
- повторить правила сравнения дробей с разными знаменателями;
- повторить правила нахождения неизвестных компонентов сложения и вычитания при решении уравнений;
- систематизировать умения решать на сложение и вычитание дробей с разными знаменателями.
Развивающий аспект:
развивать навыки анализа, сравнения материала;
содействовать развитию умений осуществлять самооценку учебной деятельности;
развивать умение находить и применять межпредметные связи;
развивать познавательный интерес к предмету с помощью экскурсов в историю; используя литературное, музыкальное и художественное наследие русского народа;
- развивать навыки компьютерной грамотности.
Воспитательный аспект:
создать у учащихся положительную мотивацию к изучению математики путем вовлечения каждого ученика в активную познавательную деятельность с опорой на исторические факты;
воспитывать потребность оценивать свою деятельность и работу товарищей;
побуждать к проявлению чувств гражданственности, патриотизма и гордости за историческую судьбу своей Родины;
воспитывать культуру речи;
- создать условия для развития коммуникативных качеств учащихся.
Формы организации учебной деятельности:
фронтальная, индивидуальная, игровая .
Метод обучения:
- творческо-поисковый .
Оборудование:
компьютер;
интерактивная доска;
проектор;
репродукции картин;
раздаточный материал (карточки с индивидуальными заданиями + дешефратор).
I. Самоопредение к учебной деятельности.
Формируемые УУД:
Личностные: самоопределение, смыслообразование.
Познавательные: целеполагание
Коммуникативные: планирование учебного сотрудничества.
Цель: Мотивация учащихся к учебной деятельности.
.Звучит запись увертюры П.И.Чайковского. Под музыку учащийся читает отрывок из произведения М.Ю.Лермонтова «Бородино».
Звучал булат, картечь визжала,
Рука бойцов колоть устала,
И ядрам пролетать мешала
Гора кровавых тел.
Изведал враг в тот день немало,
Что значит русский бой удалый,
Наш рукопашный бой!
Земля тряслась — как наши груди;
Смешались в кучу кони, люди,
И залпы тысячи орудий,
Слились в протяжный вой.
1.2. Учитель: Ребята, какое историческое событие отразил в своем произведении автор?
1.3 Учащиеся: Бородинское сражение, 7 сентября отмечалось 200-летие Бородинской битвы (26 августа по старому стилю)
1.4 Учитель:
По данным соцопроса, опубликованным в СМИ, только треть опрашиваемых знали о причинах нападения армии Наполеона, о ходе войны 1812года, о ее героях. Группе учащихся было предложено включиться в проектную деятельность: провести аналогичный соцопрос в школе, проанализировать данные и сделать выводы.
Творческий отчет группы аналитиков. Презентация «Домашнее задание» .
1.6 Учитель: Чему мы уже научились? (сокращать дроби, отмечать их на координатном луче, приводить к НОЗ, НОЧ, сравнивать дроби с разными знаменателями, производить с ними арифметические действия). Ребята, хотите ли вы узнать о том, какую роль сыграла математика в ходе войны 1812года, какое отражение нашла тема сегодняшнего занятия на исторической сцене 1812г (слайд №1).
1.7 Учащимся предлагается самостоятельно определить форму организации учебной деятельности.
Примерные ответы учащихся:
- в игровой форме раскрыть роль математики в ходе событий 1812г;
- групповая форма работы учит умению доказывать свою точку зрения, при этом учитывая мнения окружающих;
- индивидуальная форма работы учит ответственности за принятое решение.
1.8 Учитель: Почему вы остановили свой выбор на этих формах деятельности?
1.9. Учащиеся делают выводы: применение на уроках математики исторического и краеведческого материала расширяет кругозор, помогает лучше усвоить тему урока, занятия проходят интересно.
I1. Актуализация знаний.
Формируемые УУД:
Познавательные: анализ, сравнение, аналогия, использование знаковой системы, осознанное построение речевого высказывания.
Регулятивные: выполнение пробного учебного действия.
Коммуникативные: выражение своих мыслей, аргументация своего мнения, учёт разных мнений учащихся
Цель:
- подготовить мышление учащихся к последующим шагам учебной деятельности, организовать фиксирование каждым из них индивидуального затруднения;
- актуализировать мыслительные операции: сравнение, анализ, обобщение;
- зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов: в виде свойств и определений.
2.1. Учитель: Летом 1812 года французы начали свое наступление на Россию. Наполеон вещал «Если я возьму Киев, я схвачу Россию за ноги. Если я овладею Петербургом, я возьму ее за голову. Заняв Москву, я поражу ее сердце». Кто же смог дать отпор врагу? Узнаем об этом из устного счета.
2.2 Презентация№2
- Найдите дроби, большие 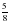 (слайд 2). Указание: надо найти правильные ответы, навести указатель мыши на «нужную» мишень и выполнить клик. Если задание выполнено верно, то произойдет выстрел из пушки. В результате получится галерея портретов героев войны 1812.
(слайд 2). Указание: надо найти правильные ответы, навести указатель мыши на «нужную» мишень и выполнить клик. Если задание выполнено верно, то произойдет выстрел из пушки. В результате получится галерея портретов героев войны 1812.
Группа экспертов из числа учащихся, выбирая материал из предложенной статьи, дает краткий библиографический материал о каждом из них (приложение №1)
- Выберите дроби, удовлетворяющие неравенству 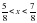 (слайд 3). Указание: надо найти правильные ответы, навести указатель мыши и выполнить клик. Если дроби найдены верно, то появится слово «Москва». Учащиеся объясняют смысл фразы из «Евгения Онегина» « …Москва, спаленная пожаром, французу отдана.»
(слайд 3). Указание: надо найти правильные ответы, навести указатель мыши и выполнить клик. Если дроби найдены верно, то появится слово «Москва». Учащиеся объясняют смысл фразы из «Евгения Онегина» « …Москва, спаленная пожаром, французу отдана.»
Примерные ответы учащихся:
-Москва, спаленная и частично разрушенная, стала препятствием для дальнейшего продвижения наполеоновского войска;
- отсутствие провианта, зимняя стужа и страстный отпор врагу расстроили «наполеоновские» планы.
- Не выполняя вычислений, поставьте вместо * знак (слайды 4 – 8):
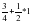 ;
; 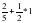 ;
; 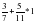 ;
; 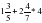 ;
; 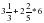
Указание: навести указатель мыши на знак и выполнить клик. Если знак выбран верно, то он займет свое место в неравенстве, если знак определен неверно, то компьютер предложит подумать еще.
Учащиеся аргументируют свои ответы, доказывают правильность решения.
III. Выявление места и причины затруднения
Формируемые УУД:
Познавательные: анализ, сравнение, обобщение, подведение под понятие, постановка и формулирование проблемы, построение речевого высказывания.
Регулятивные: волевая саморегуляция в ситуации затруднения.
Коммуникативные: выражение своих мыслей, аргументация своего мнения, учёт разных мнений, разрешение конфликтной ситуации.
Цель: Организовать анализ учащимися возникшей ситуации и на этой основе подвести их к выявлению места и причины затруднения.
Для выявления места и причины затруднения представитель из каждой группы должен быстро и рационально решить группу примеров на доске.
а) 8/15-2/3+2/15; б) 17/27- (8/27+1/5); в) (13/18+6/7)- (2/9+5/14).
3.2 Учитель (для остальных учащихся)
Нам с вами вразброс даны части алгоритма по сложению и вычитанию дробей с разными знаменателями. Работая в парах, обсудите 30 секунд, восстановите алгоритм по шагам.
1. Знаменатель оставить без изменения, записав его в знаменатель суммы (или разности).
2. Если возможно, сократить полученную дробь и выделить из нее целую часть.
3. Сложить (или вычесть) числители и записать ответ в числитель суммы (или разности).
4. Суммой (или разностью) дробей является дробь
5. Привести дроби к НОЗ, найти дополнительные множители.
Рассматривая решение предложенных примеров различными способами, выявляем путем совместных рассуждений наиболее рациональный способ, аргументируем свой выбор; на доске одна из групп восстанавливает алгоритм по сложению и вычитанию дробей.
Образец записи правильного решения примеров на доске:
а) 8/15-2/3+2/15= (8/15+2/15) -2/3= 10/15-2/3= 2/3-2/3=0
б) 17/27-(8/27+1/5)= (17/27-8/27)-1/5=9/27-1/5=1/3-1/5=5/15-3/15=2/15
в)(13/18+6/7)-(2/9+5/14)=(13/18-2/9)+(6/7-5/14)=(13/18-4/18)+(12/14-5/14)= =9/18+7/14=1/2+1/2=1
IV. Организация проектной деятельности (работа в группах).
Формируемые УУД:
Личностные: самоопределение, смыслообразование.
Познавательные: анализ, синтез, обобщение, аналогия, самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации, проблема выбора эффективного способа решения, планирование, выдвижение гипотез и их обоснование, создание способа решения проблемы.
Регулятивные: волевая саморегуляция в ситуации затруднения.
Коммуникативные: выражение своих мыслей, аргументирование своего мнения, учёт разных мнений зафиксировать, планирование учебного сотрудничества со сверстниками, достижение общего решения.
Цель: организовать коммуникативное взаимодействие для создания мини проекта;
4.1 Учитель: Творчество в математике только приветствуется. Ребята, вам предлагаются несколько репродукций «Конец Бородинского боя», «Ополчение», «Совет в Филях» (слайды 9-11). Используя иллюстрации и подобранный к ним текст (приложение №2) необходимо отобрать интересующие нас факты и на их основе выполнить творческое задание - составить пример, уравнение, задачу по выбору.
4.2 Время выполнения -7 минут, форма работы - групповая.
4.3 Учащиеся в ходе работы заполняют «Листок личных достижений» (слайд №13).
V. Защита мини проектов.
Формируемые УУД:
Личностные: осознание ответственности за общее дело.
Познавательные: построение логической цепи рассуждений, анализ, обобщение.
Коммуникативные: выражение своих мыслей, использование речевых средств для решения коммуникационных задач, достижение договорённости и согласование общего решения.
Цель: содействовать формированию системы знаний, обеспечивающих патриотическое отношение к историческому прошлому своей страны.
5.1 Учитель: время выполнения задания подходит к концу; каждая группа презентует свой проект. Представителям выделяется до 2 минут времени на анализ задания и подведение итогов.
Примерные задания
1группа (репродукция «Конец бородинского боя», Василий Васильевич Верещагин,1899г)
Под Бородино сражались 135000 французских и 120000 русских воинов. В ходе боевых действий погибло58, 5 тысяч французов и 45, 6 тысяч русских. Сравнить потери двух армий.
Решение:
58500:135000=58500 /135000= 585/1350=13/30- такая часть французских солдат погибла.
45600:120000= 45600/120000=456/1200=19/50.-такая часть русских солдат осталась на поле боя
Сравним дроби, предварительно приведя их к общему знаменателю:
13/30=13*5/30*5=65/150. и 19/50=19*3/50*3=57/150, отсюда, 65/15057/150.
4) 65/150-57/150=8/150(ч) -на столько потери французской армии были больше.
2 группа ( репродукция «Совет в Филях», Алексей Данилович Кившенко,1880г)
До нашествия Наполеона в Москве имелось 330 храмов, 9160 жилых домов, из которых только 2567 были каменными. В результате пожара, продолжавшегося на протяжении пяти дней (с 2 по 6 сентября), было уничтожено 6412 жилых домов, 121 храм и 8521 торговое помещение.
Сравнить степень разрушения в Москве жилых домов и храмов при пожаре 1812г.
Решение:
121:330=121/330=11/30- такая часть храмов была разрушена.
6412:9150=6412/9150=7/10- такая часть жилых домов была разрушена.
Сравним дроби, предварительно приведя их к общему знаменателю:
7/10=7*3/10*3=21/30 .
11/30
3.группа (репродукция «Ополчение», Илларион Михайлович Прянишников,1812г ).
Московское ополчение составляло 30 тысяч ратников. Петербургское же ополчение состояло из 15 дружин, дружина состояла из 4 сотен, а сотня- из 200 ополченцев.
Какой процент составляло петербургское ополчение от московского?
Решение:
15*4*200=12000(ч)- петербургское ополчение.
12000/30000= 12/30=2/5=0,4-такую часть составляло петербургское ополчение от московского ополчения.
О,4=40%
Ответ.40% составляло петербургское ополчение от московского ополчения.
VI. Самостоятельная работа с проверкой по эталону.
Формируемые УУД:
Познавательные: анализ, синтез, аналогия, классификация, подведение под понятие, выполнение действий по алгоритму
Регулятивные: контроль, коррекция, самооценка.
Цель: проверить своё умение применять алгоритм сложения и вычитания в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
6.1. Учитель.
А сейчас каждый проверит сам себя – насколько он сам понял алгоритм сложения и вычитания и может его применить. Для самостоятельного решения учащимся выдаются пакеты с индивидуальными заданиями и дешефраторы к ним.
I вариант
1. Выполните действия: 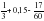 .
.
2. Решите уравнение : 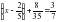 .
.
3. Решить задачу.
На отрезке АD отмечены точки В и С так, что точка С лежит между точками В и D. Известно, что АВ = 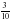 м, ВС больше АВ на
м, ВС больше АВ на 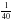 м, а СD меньше АВ + ВС на
м, а СD меньше АВ + ВС на 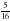 м. Найдите длины отрезков а)ВС б)СД. в) АD.
м. Найдите длины отрезков а)ВС б)СД. в) АD.
II вариант
1. Выполните действия : 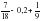 .
.
2. Решите уравнение : 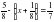 .
.
3. Решить задачу.
На отрезке MK отмечены точки N и P так, что точка N лежит между точками M и P. Известно, что MN = 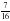 м, NP меньше MN на
м, NP меньше MN на 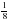 м, а PK меньше MP на
м, а PK меньше MP на 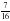 м. Найдите длины отрезков а) N P б) PK в)MK.
м. Найдите длины отрезков а) N P б) PK в)MK.
III вариант
1. Выполните действия 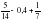 .
.
2. Решите уравнение 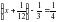 .
.
3. Решить задачу.
На отрезке АD отмечены точки В и С так, что точка B лежит между точками A и C. Известно, что АВ = 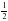 м, AB больше BC на
м, AB больше BC на 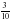 м, а AC больше CD на
м, а AC больше CD на 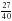 м. Найдите длины отрезков а) ВС б) СД в) АD.
м. Найдите длины отрезков а) ВС б) СД в) АD.
IV вариант
1. Выполните действия 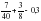 .
.
2. Решите уравнение 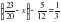 .
.
3. Решить задачу.
На отрезке MK отмечены точки N и P так, что точка P лежит между точками N и K. Известно, что MN = 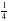 м, MN меньше MP на
м, MN меньше MP на 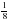 м, а MP больше PK на
м, а MP больше PK на 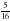 м. Найдите длины отрезков а) МР , б) РК, в) MK.
м. Найдите длины отрезков а) МР , б) РК, в) MK.
6.2 После выполнения работы учащиеся проверяют свои ответы с помощью дешефратора, который представляет собой высказывания исторических личностей о войне1812г. (слайд №17).
Решение 1 варианта.
1) 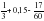 = 1/3+15/100-17/60= 1/3+3/20-17/60= 20/60+9/60-17/60=12/60=1/5.
= 1/3+15/100-17/60= 1/3+3/20-17/60= 20/60+9/60-17/60=12/60=1/5.
2) 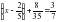
(Х-2/5)+8/35=15/35
Х-2/5=15/35-8/35
Х-2/5=7/35
Х-2/5=1/5
Х=1/5+2/5
Х=3/5. Ответ.3/5
3) 3/10+1/40=12/40+1/40=13/40(м)-длина отрезка ВС
3/10+13/40=12/40+13/40=25/40=5/8(м) –длины отрезков АВ и ВС
5/8-5/16=10/16-5/16=5/16(м)-длина отрезка СД
3/10+13/40+5/16= 24/80+26/80+25/80=75/80=15/16(м) –длина отрезкаАД
Ответ. 15/16м длина отрезка АД
Решение 2 варианта.
1) 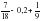 .=7/8-2/10+1/9= 7/18-1/5+1/9= 35/90-18/90+10/90=27/90=3/10=0,3
.=7/8-2/10+1/9= 7/18-1/5+1/9= 35/90-18/90+10/90=27/90=3/10=0,3
2) 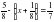
5/8-х-1/8=1/7
4/8-х=1/7
Х= 4/8-1/7
Х=28/56-8/56
Х=20/56
Х=5/14.
Ответ. 5/14.
3) 7/16-1/8=7/16-2/16=5/16(м) –длина отрезка NP
7/16+5/16=12/16(м) –длина МР
12/16-7/16=5/16(м)-длина отрезка РК
7/16+5/16+5/16=17/16= 1 1/16(м)-длина отрезка МК
Ответ.1 1/16 м длина отрезка МК.
Решение 3 варианта.
1 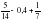 =5/14-4/10+1/7=5/14-2/5+1/7=25/70-28/70+10/70=35/70-=28/70=7/70=1/10=0,1
=5/14-4/10+1/7=5/14-2/5+1/7=25/70-28/70+10/70=35/70-=28/70=7/70=1/10=0,1
2)
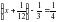 .
.
Х+1/12 =3/12+4/12
х+1/12 =7/12
х=7/12-1/12
х=6/12
х=1/2
Ответ.1/2
½-3/10=5/10-3/10=2/10=1/5(м)-длина отрезка ВС
½+1/5=5/10=2/10=7/10(м)- длина АС
7/10-27/40=28/40-27/40=1/40(м)- длина СД
½+1/5=1/40=20/40+8/40+1/40=29/40(м)-длина отрезка АД
Ответ.29/40 м длина отрезка АД
Решение 4 варианта.
1) 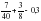 = 7/40+15/40-12/40=10/40=1/4.
= 7/40+15/40-12/40=10/40=1/4.
2) 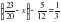
23/20-х= 4/12+5/12
23/20-х=9/12
23/20-х= ¾
Х= 23/20-15/20
Х= 8\20
Х= 2/5.
Ответ. 2\5
¼+1/8= 2/8+1/8=3/8(м) –длина отрезка МР
3/8-5/16=6/16-5/16= 1/16(м)-длина отрезка РК
3/8+1/16= 6/16+1/16=7/16(м) –длина отрезка МК
Ответ. 7/16 м длина отрезка МК
VII. Рефлексия деятельности на уроке
Формируемые УУД:
Познавательные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха или неуспеха.
Коммуникативные: аргументация своего мнения, планирование учебного сотрудничества.
Цель:
-зафиксировать новое содержание, изученное на уроке: алгоритм сложения и вычитания дробей;
-оценить собственную деятельность на уроке;
-поблагодарить одноклассников, которые помогли справиться с заданиями урока;
-зафиксировать неразрешённые затруднения как направления будущей учебной деятельности: действия со смешанными числами;
- обсудить и записать домашнее задание.
7.1 Организация учебного процесса на этапе.
Учитель:
– Какую цель мы ставили в начале урока?
– Что нового узнали на уроке?
– Наша цель достигнута?
– Какие знания нам пригодились при выполнении заданий на уроке?
– Как вы можете оценить свою работу? (слайд №.18.)
7.2
Учитель. «Французы показали себя достойными одержать победу, а русские стяжали право быть непобедимыми» - подводил итоги военной кампании Наполеон. А мы показали себя победителями? Тогда давайте поговорим о наградах (слайды № 14-16).
7.3 Учитель предлагает учащимся выбрать на память об уроке фотографию
понравившегося ордена (звучат фанфары).
7.4 Домашнее задание по выбору (слайд № 19):
- «Интервью с героем».
- Тетрадь на печатной основе по математике. стр 55 №5-7.
7.5 Участники урока благодарят одноклассников, гостей за сотрудничество.
Выводы по 2 главе
Таким образом, во второй главе были проанализированы понятия «обыкновенная дробь» и «десятичная дробь» с использованием краеведческого материала в 5-6 классах, и операции над дробями (Сравнения обыкновенных дробей с одинаковыми знаменателями, сравнение дробей с одинаковыми числителями, сравнение дробей с разными знаменателями, операции сложение и вычитание дробей с одинаковыми знаменателями, сложение и вычитание дробей с разными знаменателями, операция умножения дробей, операция деления дробей, сравнение десятичных дробей, сложение и вычитание десятичных дробей, алгоритм умножения, алгоритм деления десятичной дроби на натуральное число, алгоритм деления на десятичную дробь.) с использованием конкретных краеведческих задач.
Заключает и обобщает вторую главу конспект урока «Бородино» с использованием исторических фактов, который ставит перед собой такие цели:
Образовательный аспект:
в ходе совместной, индивидуальной работы:
- повторить и углубить знания по теме «Бородино»;
- повторить правила сравнения дробей с разными знаменателями;
- повторить правила нахождения неизвестных компонентов сложения и вычитания при решении уравнений;
- систематизировать умения решать на сложение и вычитание дробей с разными знаменателями.
Развивающий аспект:
развивать навыки анализа, сравнения материала;
содействовать развитию умений осуществлять самооценку учебной деятельности;
развивать умение находить и применять межпредметные связи;
развивать познавательный интерес к предмету с помощью экскурсов в историю; используя литературное, музыкальное и художественное наследие русского народа;
- развивать навыки компьютерной грамотности.
Воспитательный аспект:
создать у учащихся положительную мотивацию к изучению математики путем вовлечения каждого ученика в активную познавательную деятельность с опорой на исторические факты;
воспитывать потребность оценивать свою деятельность и работу товарищей;
побуждать к проявлению чувств гражданственности, патриотизма и гордости за историческую судьбу своей Родины;
воспитывать культуру речи;
- создать условия для развития коммуникативных качеств учащихся.
Заключение.
Тема данной курсовой работы продолжает и углубляет изучение дробей с использованием краеведческого материала, что необходимо в настоящее время, так как возрастает ценность образования, изменяется содержание, задачи и цели обучения, а также и требования, предъявляемые к уровню знаний учащихся. А при обучении выполнению заданий, связанных с дробями с использованием краеведческого материала, учащийся приобретает способность к научно-исследовательской деятельности.
В работе путем строгого аналитического изложения вводятся некоторые важные понятия и определения, способствующие успешному пониманию темы. А также присутствуют методические положения, которые способствуют наиболее успешному, понятному и качественному изучению дробей в 5-6 классах.
Данная курсовая работа содержит не только теоретический материал, но и практический (конспект урока). В работе рассмотрены основные понятия, их свойства и задачи; методы и решения краеведческих задач.
В данной работе не столько пересказ учебного материала, отраженного во многих школьных учебниках, сколько акцентуализация внимания на некоторых вопросах, которые вызывают наибольшую методическую трудность.
Так как в курсовой работе содержатся основы школьного курса математики по теме “Дроби”, то она будет полезна студентам педагогических вузов, учителям, школьникам, готовящимся к поступлению в вузы, учащимся школ и классов с углубленным изучением математики.
Список использованной литературы.
Краеведение в школе// Педагогическая энциклопедия. — М., 1965. -518с
Романов Ю.В., Спица М.А. Классификация исторических задач в обучении математике // Модернизация образования. – 2012.
Колягин Ю.М. Задачи в обучении математике: Часть I.: Математические задачи как средство обучения и развития учащихся. – М.: Просвещение, 1977. – 110
Ким Н.А. Справочник учителя математики – Волгоград: Издательство «Учитель», 2011.
Лященко, Е.И. Лабораторные и практические работы по методике преподавания математики: Учеб. Пособие для студентов физ. - мат. спец. пед. ин-тов / Е.И. Лященко. - М.: Просвещение, 1988, - 223 с.
Методика преподавания математики в средней школе. Частная методика [Текст]: Учеб. пособие для студентов пед. ин-тов по физ. - мат. спец. / А.Я. Блох, В.А. Гусев, Г.В. Дорофеев; Сост.В.И. Мишин. - М.: Просвещение, 1987. - 416 с.
Канин, Е.С. Учебные математические задачи: Учебное пособие. / Е.С. Канин - Киров: Издательство ВятГГУ, 2003. - 191 с.
Математика - 5 кл. / под ред. Виленкина Н.Я., Жохова В.И. - М.: Мнемозина, 2006.
Математика - 6 кл. / под ред. Виленкина Н.Я., Жохова В.И. - М.: Мнемозина, 2006
Математика. Подготовка к ЕГЭ-2010. Вступительные испытания. Л.Д.Лаппо, М.А.Попов. –М.: издательство «Экзамен»,2010.
Подтверждение авторства
Пожалуйста, введите ваш Email.
Если вы хотите увидеть все свои работы, то вам необходимо войти или зарегистрироваться
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
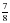 сада:
сада: