Методика формирования эвристических приёмов на уроках математики в 5-6 классах

АНО ВПО «Европейский Университет «Бизнес Треугольник»

Дипломная работа

по дополнительной профессиональной образовательной программе

профессиональной переподготовки

«Педагогическое образование: Учитель математики»

Тема:

”Методика формирования эвристических приёмов на уроках математики в 5-6 классах”

Дипломную работу подготовил

Пигарев Андрей Алексеевич

Должность:

Учитель математики

Место работы:

Новосельская ООШ

Ленинградская область, Сланцевский район

Новосельское сельское поселение

Российская Федерация

Содержание

Введение………………………………………………………………………………………3

Глава 1. История и общая характеристика эвристического метода обучения………………………………………………………………………………………5

1.1 Основные понятия эвристики……………………………………………………………….5

1.2 Разновидности и функции эвристик в обучении математике.......................................8

1.3 Творческое мышление как результат эвристического обучения...................................11

1.4 История эвристического обучения. Общая характеристика эвристического метода обучения...........................................................................................................................14

1.5 Обзор известных эвристических приемов....................................................................20

Глава 2. Методические особенности формирования эвристических приёмов на уроках математики в 5-6-х классах........................................26

2.1 Пути и условия организации эвристического обучения в школе...................................26

2.2 Формирование эвристических приемов при обучении математике учащихся 5-6-х классов.............................................................................................................................29

2.3 Эвристический урок по математике.............................................................................43

Заключение................................................................................................................46

Литература...................................................................................................................48

Введение

В условиях стремительного прогресса науки и техники, знания быстро устаревают, поэтому наше время от современного человека требует таких качеств как инициативность, изобретательность, умение безошибочно немедля принимать те или иные решения. В связи с этим встает актуальность эвристического обучения и школа должна уделять большое внимание развитию творческих способностей своих подопечных, воспитанию деятельной личности.

Упор на раскрытие и развитие творческих способностей детей делается во многих странах мира. Овладение изучаемым материалом не достаточно, необходимо также умение применять это на практике, решать возникающие проблемы. И воспитать подобную личность можно лишь педагогической деятельностью, которая предоставляет все для раскрытия творческого потенциала. В связи с этим, раскрытие и развития творческих способностей школьников с помощью эвристики является актуальным на сегодняшний день.

Я.А. Коменский писал: «… школа не показывает самые вещи, как они происходят из самих себя и каковы они в себе, но сообщала, что о том и другом предмете думает и пишет один, другой, третий и десятый автор». Это значит что тот, кто за ребенка определяет его цель, берет на себя ответственность судьбы, рискует деформировать характер, навязать ложные стереотипы мышления. «Ребенка надо учить и развивать всесторонне, чтобы дать возможность проявится его скрытым, может быть очень глубоко, способностям».[8].

Дипломная работа имеет цель понять , что такое эвристика, как формируются эвристические приемы, разработать вопросы (проблемы, задачи) которые создадут условия возникновения эвристических приемов.

Научение математике школьников 5 – 6 классов , является объектом данной дипломной работы.

Предмет - эвристических приемы в процессе обучения математике учащихся 5-6 классов.

Согласно исследованиям дидакты [13, 14], обучение творчеству школьников – это вооружение их умением осознавать проблему, намеченную учителем, а позднее – формулировать ее самому. Это развитие способностей выдвигать гипотезы и соотносить их с условиями задачи, осуществлять поэтапную или итоговую проверку решения несколькими способами; способностей переноса знаний и действий в нестандартную ситуацию или создания нового способа действий.

Наше время диктует современной школе требования, которые обеспечивают ребенка возможностью приобретать самостоятельно новые знания из окружающего его мира и развивают эвристическое мышление.ГЛАВА 1. История и общая характеристика эвристического метода обучения

1.1 Основные понятия эвристики

Эвристика (от греч. heurisko – нахожу) – методология научного исследования, а также методика обучения, основанная на открытии или догадке.

Эвристическая деятельность, эвристические приемы, эвристические методы, эвристические беседы, эвристические задачи – это основные понятия эвристики. Рассмотрим их ниже.

Термин «эвристика» понимается в различных значениях:

1) наука, изучающая продуктивное творческое мышление (эвристическую деятельность);

Эвристическая деятельность – это специфический умственный процесс, разновидность человеческого мышления, создающее новую систему действий, открытие неизвестных ранее закономерностей объектов (или объектов изучаемой науки).

2) Эвристические приемы это приемы, которые родились в процессе решения одних задач и более или менее сознательно переносятся на другие задачи.

3) эвристические методы применяются в открытии чего-то нового;

Дать четкое определение эвристическому методу до сегодняшнего дня никто не смог. Многие авторы считают этот метод эффективным, но недостаточно безотказным. Он позволяет сократить перебор путей решений, до того как принят уже окончательно нужный путь. И такое понимание термина “эвристический метод” не раскрывает сомой сути этого явления, а только описывает его внешнюю форму.

Эвристический метод дает возможность школьнику обрести больше свободы действий в творческом поиске.

Задача педагога при выборе методик, формирующих творческие способности детей эвристическим методом, не упустить такие факты как:

-Подготовленность аудитории;

-Индивидуальность каждого ребенка;

-Специфику преподаваемого предмета.

Для выращивания творческих способностей, необходимы также условия, перечислим их:

-Мотивация учения;

-Творческая активность;

-Дружественная обстановка в коллективе;

-Сильные эмоции.

Поэтому учитель должен будет следить за тем, чтобы

-Багаж знаний по математике у учащихся равномерно пополнялся;

-Повышался уровень общеучебных умений и навыков;

-Развивалось самостоятельность в творческой деятельности;

4) Эвристические беседы (Сократичекий метод обучения)

Беседа – это старый метод дидактической работы. Сократ (отсюда и термин “сократические беседы”) очень умело использовал этот метод. Считая, что он сам не знает истины, помогал родиться ей в своем собеседнике. Свой метод он уподоблял повивальному искусству – профессии его матери, называя его майевтикой. Подобно тому, как та помогала рождаться детям, Сократ помогал рождаться истине.

5) эвристика - направленность деятельности человека, ориентированную на создание им субъективно или объективно нового и значимого продукта. В данном контексте эвристика отождествляется с мотивом творческой деятельности.

6) эвристика - любой совет, как разрешить проблему. В этом контексте понятие эвристики настолько объемно, что как-то классифицировать его не так-то легко. Эвристикой, в данном случае, будем называть любой способ решения задачи или доказательства теоремы.

Обучение эвристикам происходит по мере усвоения учебного материала. Решая задачи учащиеся, к примеру, обучаются таким эвристическими приемами как достраивание фигуры до конфигурации, рассмотрев которую ребенок приблизится к ответу. Можно завести отдельную тетрадь для эвристик и по мере надобности пользоваться ею.

Для взращивания математических способностей учитель должен включать в план урока задачи на сообразительность, задачи-шутки, математические ребусы

Пример задачи на сообразительность: Некий человек должен был перевезти в лодке через реку волка, козу и капусту. В лодке мог поместиться только один человек, а с ним или волк, или коза, или капуста. Но если оставить волка с козой без человека, то волк съест козу, если оставить козу с капустой, то коза съест капусту, а в присутствии человека «никто никого не ел». Человек все-таки перевез свой груз через реку. Как он это сделал? (Ответ: Волк не ест капусту, следовательно, начинать переправу надо с козы, так как волка и капусту можно оставить на берегу без человека. Переправив козу на другой берег, человек возвращается, берет в лодку капусту и также перевозит ее на другой берег, где ее оставляет, но зато берет в лодку козу и везет ее обратно – на первый берег. Здесь он козу оставляет и перевозит волка, а сам возвращается за козой, перевозит ее, и переправа оканчивается благополучно.)

Пример задачи – шутки: Приготовьте 8 бумажек с числами 1, 2, 3, 4, 5, 7, 8 и 9 и расположите их в два столбца таким образом (рис. 1).

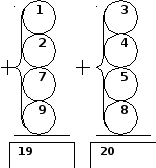
Рисунок 1

Обменивая местами всего лишь две бумажки, добейтесь того, чтобы суммы чисел в обоих столбцах были одинаковыми. (Ответ: Поменять местами бумажки с числами 8 и 9, при этом 9 перевернуть как 6. тогда в каждом столбике будет по 18).

7) Эвристические задачи – задачи, для решения которых необходимо выявить некоторые скрытые связи между элементами условия и требования или найти способ решения, причем этот способ не является очевидной конкретизацией некоторого обобщения правила, известного ученику, или сделать и то и другое [1].

Сталкиваясь с эвристическими задачами школьник должен уметь применять эвристические методы и приемы: прием элементарных задач, прием представления задачи в пространстве состояний, прием рассмотрения предельного случая, прием вспомогательной фигуры, которые составляются базовыми и специальными эвристиками.

1.2 Разновидности и функции эвристик в обучении математике

Классификация эвристик даст нам более четкое понимание эвристик как эвристических приемов.

Труды по психологии советуют приемы деятельности классифицировать по следующим основаниям: по степени обобщения приема; по степени обобщенности цели; по форме операционного состава; по возможности достижения цели. Поэтому в качестве оснований для классификации эвристик принимают основания, отнесенные к структурным элементам.

Степень обобщенности приема (Основание первое).

Здесь эвристики делятся на:

- общие эвристики. Цель – выявление общих закономерностей, для решения задач любого рода.

Структурными элементами являются эвристические приемы мыслительной деятельности и эвристические ориентиры;

- специальные эвристики, Цель – выявление конкретных математических закономерностей.

Структурными элементами специальных эвристик являются эвристические предписания, диалогические концентры, базовые эвристики решения эвристических задач;

Степень обобщенности цели (Основание второе)

Эвристические приемы мыслительной деятельности.

Эту группу образуют приемы мыслительной деятельности, делящиеся следующим образом.

1. Общие (анализ, синтез, сравнение, абстрагирование, классификация, систематизация, аналогия и другие).

2. Специфические (к ним относят: подведение под понятие, выведение следствий и так далее);

Эвристические ориентиры.

1. Общие эвристические ориентиры. К ним относятся:

- правила ориентиры;

- правила – советы;

- эвристический довод;

- эвристическое рассуждение;

- эвристические схемы;

- стратегии и др.

2. Эвристические ориентиры специфического характера – сужают поиск решения, но не всегда дают нужный результат.

- нарисуй картинку;

- начерти фигуру;

- подразделяй на случаи;

- обращай действия;

- рассуждай от противного;

- обобщи;

- действуй по аналогии;

- выделяй главное (главную часть) и др.

Диалогические концентры.

Прием, при котором всякое существенно важное математическое понятие после его введения погружают в диалог с другими понятиями с целью востребованности основных знаний и систематизации.

Базовые эвристики решения эвристических задач - эвристические приемы зародившиеся при решении одних задач и которые могут переноситься на решение других задач.

- рассмотрение предельного случая;

- введение вспомогательных неизвестных;

- введение дополнительных элементов (дополнительных построений);

- переход к равносильной задаче;

- выделение подзадач;

- контрпример и подтверждающий пример.

Система эвристически – ориентированных задач.

Эта система эвристических задач, которые мотивируют эвристическую деятельности школьников.

Следующие эвристики часто используются в 5-6 классах:

Анализ задачи – всегда направлен на обнаружение внутренних связей. Это эвристический прием, действие, которое начинается с того, что необходимо найти, построить или доказать к тому, что дано или установлено.

Пример: Вычислите: (9-(9-(9-…-(9-1)…))). В записи 100 пар скобок.

Введение вспомогательного элемента – это эвристический прием, используемый в математике для формоизменения текстовой задачи. Суть его заключается в следующем. Если в выражение, равенство или неравенство входят переменные или выражение определенной областью значений, то можно заменить одну или несколько переменных выражениями, имеющие ту же область значений.

Примером задачи для 5 класса может служить: Среднее арифметическое трех чисел равно 0,48. Первое число равно 0,4, а второе в 1,8 раза больше первого. Найдите третье число. (Ответ: 0,32)

Перебор. Строится на организованном разборе всех или некоторых специально выбранных случаев, которые возможны в ситуации, описанной в задаче. Если рассматриваются все случаи – перебор полный, в противном случае – сокращенный.

Перебор бывает двух видов: рассмотрение каждого случая в отдельности и групповой анализ возможных решений. Каждый случай рассматривается отдельно, если вариантов решения немного и практически это возможно.

Если разбор каждого случая не возможен или затруднителен, пользуются сокращенным перебором. Чтобы ограничить полный перебор и получить сокращенный, пользуются такими приемами как: исключение заранее известных вариантов, разбор взаимозаменяемого случая, установления границ поиска и т.д..

Пример задачи 5 класса: существуют трехзначные числа. Сумма цифр которого равна девяти. Найти эти числа.

Эвристика выполняет многие дидактические функции:

1) средства предпочтения при выборе каких-либо действий;

2) Систематизация изученного и изучаемого материала;

3) способ нахождения аналогии;

4) "добывание" знаний;

5) способ становления диалога;

6) способ приводящий к математическому открытию;

1.3 Творческое мышление как результат эвристического обучения

Учитель, применяя эвристический или какой другой принцип развития творческого мышления должен учитывать возрастные и индивидуальные особенности мышления. Этому посвящены труды многих известных авторов. В них определена стадиальность развития интеллекта, подробно описана каждая стадия в зависимости от ведущего вида мыслительной деятельности.

Первая стадия – стадия «мышление руками»(это относится к маленьким детям). Ведущим является наглядно-действенное, практическое мышление.

Вторая стадия - наглядно-образное мышление. Оно дает возможность оперировать уже не реальными предметами, а образами восприятия и представлений, которые ребенок получил на собственном опыте. Мышление еще связано с действиями, но эта связь уже не такая прямая, как раньше. Теперь ребенку, чтобы решить задачу, необходимо отчетливо прорисовать ее в своем воображении, наглядно воспринять.

Далее мышление начинает принимать форму отвлеченных понятий и рассуждений, по поводу окружающей нас реальности в поиске закономерных связей между ними. И это третья стадия развития, главную роль, в которой берет на себя отвлеченное, абстрактно-теоретическое мышление. Большое значение в умственном развитии учеников имеет изучение и овладение теориями, законами, понятиями, что дает большие возможности для творчества.

Оптимальное развитие всех трех видов деятельности: и абстрактно-теоретического, и наглядно-образного, и наглядно-действенного, практического мышления, является важным условием для развития эвристического мышления.

При решении задач на основе формально-логического анализа, перепробовав все известные способы и не добившись успеха, обязательно возникнет потребность в новых знаниях, которые помогут решить проблему, эта потребность придаст человеку высокую активность в решении данной проблемы, здесь и возникает эвристическое мышление. Там где удельный вес продуктивности высок, можно говорить о творческом мышлении, как об особо эффективном виде мышления. Здесь возникает что-то оригинальное и имеет высокую степень новизны. Проблемные ситуации - вот, что служит основанием для возникновения творческого мышления, ситуации, способствующей осознанию потребности в открытии новых знаний, стимулирующей высокую активность решающего проблему субъекта.

Проблема возникающая в отношениях, закономерных связей между признаками, заставляет человека открывать новые, не известные ему ранее признаки, существенные для решения данной проблемы. Он вынужден действовать в условиях неопределенности, выдвигать гипотезы, осуществлять выбор между ними (иногда не имея достаточных оснований для этого),проверять. Каждая гипотеза имеет свое предвидение того что может быть получено. И большую помощь в этом оказывают обобщения, которые позволяют сократить число гипотез.

Л. Л. Гурова [4] предлагает , весьма плодотворным в поиске пути решения проблемы оказывается ее содержательный, семантический анализ, направленный на раскрытие натуральных отношений объектов, о которых говорится в задаче. В нем существенную роль играют образные компоненты мышления, которые позволяют непосредственно оперировать этими натуральными отношениями объектов. Они представляют собой особую, образную логику, дающую возможность устанавливать связи не с двумя, как при словесном рассуждении, а со многими звеньями анализируемой ситуации, действовать, по словам Л. Л. Гуровой, в многомерном пространстве.

Новые вопросы требуют новых путей поиска ответов. И в этой связи на ряду со словесно-логическими обобщениями (которые очень хорошо осознаются), не найдя адекватного выражение в слове, необходимы интуитивно-практические обобщения, которые появляются в результате наглядных действий при поиске ответов (действия с реальными предметами их моделями). Этот путь облегчает поиск, но сам при этом остается вне ясного осознания.

Само интуитивно-практическое мышление осознается как мгновенное озарение(хотя сам процесс может быть довольно широко растянут во времени), которое человек получает не обязательно в процессе поиска ответа. Сначала выстреливает сам ответ, а путь его достижения осознается только после глубокой осознанной мыслительной деятельности.

В этом процессе, как отмечает К. А. Славская, нередко имеет место внешне внезапное усмотрение пути решения - «инсайт», «ага-переживание», причем оно часто возникает тогда, когда человек непосредственно не был занят решением проблемы. Реально такое решение подготовлено прошлым опытом, зависит от предшествующей аналитико-синтетической деятельности и прежде всего - от достигнутого решающим уровня словесно-логического понятийного обобщения. Однако, сам процесс поисков решения в значительной своей части осуществляется интуитивно, под порогом сознания, не находя своего адекватного отражения в слове, и именно потому его результат, «прорвавшийся» в сферу сознания, осознается как «инсайт», якобы не связанный с ранее осуществлявшейся субъектом деятельностью, направленной на открытие новых знаний.

Творческое мышление – это сдвиг в умственном развитии. Оно приводит к тому что человек меняет свойство своей личности, у него возникают новые формы психической саморегуляции, появляются новые формы психической связи. Именно поэтому эвристическую деятельность следует рассматривать как такую разновидность человеческого мышления, которая создает новую систему действий или открывает неизвестные ранее закономерности окружающих человека объектов (или объектов изучаемой науки).

В данной работе творческое мышление и эвристическая деятельность (или продуктивное мышление) – синонимы. Хотя многие психологи теоретики разделяют эти понятия. Для них продуктивным мышлением зовется мышление школьников в процессе обучения творческому мышлению, а самим творческим мышлением обозначается высшая степень мыслительной деятельности, которая приводит к принципиально новым знаниям, создание чего-то не имеющего аналога.

Творческому мышлению присущи высокая степень отклонения от привычного, преодоления «барьеров прошлого опыта», необычные решения, которые идут в разрез с жизненным опытом и т.д.. Для такого мышления важно выделить и удерживать в уме всю совокупность существенных признаков требуемых задачей и не уделять внимание случайным. Это скачкообразный, циклический процесс, в котором на первый взгляд отсутствует всякий здравый смысл, и проводником является интуиция.

1.4 История эвристического обучения. Общая характеристика эвристического метода обучения

Эвристика (от греч. heurisko - нахожу) - методология научного исследования, а также методика обучения, основанная на открытии или догадке. 1) В Древней Греции – система обучения путем наводящих вопросов; 2) совокупность логических приемов и методических правил теоретического исследования и отыскания истины; метод обучения и отыскания истины; метод обучения, способствующий развитию находчивости, активности. Большой Энциклопедический Словарь, в одной из трех трактовок эвристики, определил ее так: «Восходящий к Сократу метод обучения (сократические беседы)».

Беседу относят к наиболее старым методам дидактической работы. Ее мастерски использовал еще Сократ, от имени которого и произошло понятие «сократическая беседа». Считая, что сам он не обладает истиной, Сократ помогал родиться ей в душе своего собеседника. Свой метод он уподоблял повивальному искусству - профессии его матери, называя его майевтикой. Подобно тому как та помогала рождаться детям, Сократ помогал рождаться истине. «Истина не рождается и не находится в голове отдельного человека, она рождается между людьми, совместно ищущими истину в процессе их диалогического общения”.

Метод Сократа развивался и совершенствовался в трудах великих мыслителей и педагогов. Различные аспекты эвристического обучения нашли свое отражение в трудах Я.А. Коменского, И.Г. Песталоцци, Дж. Дьюи и др.

Ян Амос Коменский писал, что правильно обучать – это не значит вбивать в головы какую-то полезную информацию, а значит «раскрывать способности понимать вещи, чтобы именно из этой способности, точно из живого источника, потекли ручейки, ручейки живой мысли» [8].

Самым сложным для учителя считается раскрытие и развитие скрытого потенциала каждого ученика. И на наш взгляд это наиболее вероятно при использовании эвристического метода.

В нашей стране исследователи, ошибочно, в своем большинстве относили эвристический метод к проблемному и развивающему обучению. Но эвристическое обучение имеет свою специфику и тесно связано с личностно-ориентированным обучением.

В своей книге «Эвристическое обучение» [3] Хуторской А.В. дает определение и характеристики каждого метода (Таблица 1).

.

Сравнение четырех видов обучения Таблица 1

Проблемное обучение	Развивающее обучение	Личностно-ориентированное обучение	Эвристическое обучение
ОПРЕДЕЛЕНИЕ
Это система методов, приемов, правил учения и преподавания с учетом логики развития мыслительных операций и закономерностей УПД учащихся	Это ориентированность учебного процесса на потенциальные возможности учащегося и их реализацию	Это единый процесс развития индивидуальности личности, в котором личность становится субъектом собственного становления и развития	Эвристический метод - это обусловленная принципами обучения система регулятивных правил подготовки учебного материала и проведения эвристической беседы с решением познавательных задач
ЦЕЛЬ
Усвоение учениками заданного предметного материала путем выдвижения учителем специальных познавательных задач-проблем	Усвоение учащимися сообщаемых им знаний, но не репродуктивно, а в процессе их собственной деятельности	Создание психолого-педагогических и организационно-управленческих условий для «создания учеником собственного образовательного продукта или целой системы жизненных смыслов»	Эвристический подход к образованию позволяет расширить возможность проблемного обучения, поскольку ориентирует учителя и ученика на достижение неизвестного им заранее результата
СУЩНОСТЬ
Организация учителем проблемных ситуаций в уч.-позн. работе учащихся и управление поисковой деятельностью учащихся	Ученик не только усваивает конкретные знания и навыки, но и овладевает способами действия, обучается конструировать и управлять своей учебной деятельностью	Ориентация на создание условий для личностной самореализации учащихся; формирование у них потребности в самообразовании и саморазвитии	Неизвестность образовательного продукта может относится не только к ученику, но и к учителю
УЧИТЕЛЬ
Знает ответ, подводит учащихся к нему	Направляет деятельность учащихся	Совместный поиск по разрешению проблемы, взаимодействие опыта учителя и учащегося	Сочетает частичное объяснение нового с постановкой проблемных заданий. Полученный учеником продукт деятельности (гипотеза, сочинение, модель и т.п.) сопоставляется затем с помощью педагога с культурно-историческими аналогами, в результате чего данный продукт переосмысливается, достраивается или драматизируется, вызывая необходимость новой деятельности.
УЧАЩИЙСЯ
Под руководством учителя самостоятельно решает, рассуждает, делает выводы Выращивает свое собственное знание, открывает его для себя заново, но "пошагово"	Рассматривается как само изменяющийся субъект учения; Однако ему не предоставляется право самому выбирать способы и формы учебной деятельности Каждый его шаг направляется и корректируется педагогом	Субъект познания (Якиманская И.С.), субъект жизнедеятельности (Сериков В.В.), субъект культуры в целом (Бондаревская Е.В.) является полноценным субъектом деятельности	Сам ставит собственные цели, «самостоятельно» открывает зна­ния, производит методологическую и учебную продукцию. сам строит свое образование; он полноправный источник и организатор сво­их знаний, выполняют самостоятельные работы поискового типа: анализируют проблемные ситуации, ставят проблемы и решают их, находят новые знания и способы действий
МЕТОДИКА
Построена так, что ученики «наводятся» учителем на известное решение или направление решения задачи	Вовлекая учеников в учебную деятельность, педагог конструирует педагогическое воздействие на основе учета зоны ближайшего развития ребенка и его личный опыт	Создание личностно-ориентированной ситуации. Ориентирована на эффективное развитие личности обучающегося (методы проблемного и развивающего обучения)	ЭО определяет методологию образования и относится к учебному целеполаганию, созданию учащимися собственного содержания образования, рефлексивному конструированию ими теоретических элементов знаний

«Эвристическое обучение отличается от развивающего и проблемного качественно новой задачей: развитием не только ученика, но и траектории его образования включая развитие целей, технологий, содержания образования» [3].

В психологии, инженерии, физике, информатике, кибернетике, философии и других научных областях также используется эвристический подход. Специалисты каждой из этих наук толкуют эвристику, ее основные положения и понятия со своих позиций. Так, кибернетики считают, что эвристика - методы и способы, связанные с улучшением эффективности системы (человека или машины), решающей задачи. В последние годы к эвристике относят и те исследования представителей кибернетики, которые пытаются моделировать высшие проявления интеллекта. Психологи считают эвристику разделом психологии, изучающим творческое мышление. Педагоги считают эвристикой науку о средствах и методах решения задач. Философы термин "эвристический" приписывают таким правилам или утверждениям, которые способствуют открытию нового.

И все же фундамент эвристики - психология, вернее ее раздел творческого, или продуктивного, мышления. В компьютерной инженерии эвристический метод, например, дает возможность учащимся делать первые шаги к изобретательству. Разработанные эвристические приемы относятся к объекту эвристической логики, а сама эвристическая деятельность - это объект психологии. Поэтому приемы эвристики можно выразить математическим языком, но эвристическая деятельность на сегодняшний день не имеет своего математического выражения.

Эвристический приемы, как советы учителю можно встретить в книге французского педагога Лезана "Развитие математической инициативы"[12].. Здесь, правда, термин эвристика еще отсутствует. Лезан наглядно показывает, как опираясь на заинтересованность процессом обучения сделать урок более эффективным.

Дистервег показал на примере стереометрии «что для учащихся гораздо важнее узнать пути к доказательству, нежели само доказательство».

Г.Г.Воробьёв подчеркивает: «Когда учитель не совсем уверен, что получит нужный ему ответ, он…дарит идею. Дарить – в данном случае означает, что… получивший не догадывается о дарении, полагая, что это его собственная идея. Как известно, свои идеи больше волнуют, увлекают и побуждают к самореализации» [16].

К сожалению, в современной школе все еще главные усилия школьников направляются на усвоение и воспроизведение готовых знаний. Вся познавательная деятельность становится одностороней, так как внимание преподавателей устремленно только к первой функции методов – усвоению знаний, развитие познавательных способностей, вторую функцию - считают неважной. И на современном этапе найдется не много школ, имеющих творческое направление.

1.5 Обзор известных эвристических приемов

Д. Пойа [20, 21], выделил и проанализировал множество эвристических приемов, он выделяет четыре фазы решения творческой задачи и эвристические приемы распределены по этим фазам.

На первой фазе проводится разбор условия, анализируются данные и требования. В эту фазу попадают такие приемы, как:

- исследование данных задачи (достаточны ли они, или недостаточны, или противоречивы);

- построение чертежа, введение обозначений и переформулировка задачи;

- развертывание определений (заменить термины их определениями»).

Вторая фаза – плана решения. К этой фазе автор относит следующие приемы:

- решение от конца к началу;

- использование аналогичных, вспомогательных задач (частных или общих задач);

- введение вспомогательных элементов (неизвестных, более близких к искомому).

Третья фаза – реализация плана решения. Для этого необходим:

- контроль каждого шага;

- доказательство правильности каждого шага.

Четвертый этап исследование полученного решения. На этом этапе осуществляется:

- проверка результатов;

- проверка хода решения;

- поиск другого способа получения результата;

- использование полученного результата и метода решения.

Методы и приемы первой и второй фаз, явно, содержат эвристический характер.

Две фазы присутствуют у О.К. Тихомирова: фазу нахождения решения и фазу его проверки. Первая фаза включает следующие этапы:

1) «начальное обследование ситуации», т.е. ознакомление с составом элементов, установление элементов, установление функциональных связей между элементами, установление конфликта - всесторонний анализ ситуации;

2) подготовка попытки;

3) проигрывание попытки;

4) переобследование ситуации при недостижении цели;

5) новые попытки в том же составе.

этапы 2-5 – приемы работы с гипотезами: выдвижение, проверка, анализ.

Ю.Н. Кулюткин пишет следующее: «Усвоение школьником обобщенных связей и зависимостей внешнего мира, переход от конкретного к абстрактному составляет главное условие развития творческого мышления. Вместе с тем чрезвычайно важно формировать у учащихся и сами приемы вычленения отношений (эвристики)» [15]. выделяет следующие разновидности эвристик:

1. Прием упрощения (временной редукции) некоторых отношений и связей между объектами. Этот прием в зависимости от содержания задач можно проводить двумя разными путями.

а) Если в задаче определяется система одновременных взаимодействий между различными составляющими, то упрощение заключается в предварительном «разведении», дивергенции этих взаимодействий.

б) Если в задаче определяется система последовательных воздействий, то упрощение заключается в конвергенции, «сокращении», «укрупнении» отдельных этапов.

Понятно, что в обоих случаях упрощение носит временный характер, и производится для того, чтобы построить некоторую исходную гипотезу. Как только исходная гипотеза возникает, на задачу вновь накладываются ограничения.

2. Прием переформулирования - временный отказ от определенности какой-то одной формулировки, продуцирование ряда тождественных формулировок.

3. Прием решения «от начала» и «от конца» - сокращает длину последовательных преобразований сразу с двух сторон.

4. Прием «блокирования» составляющих - вначале преобразуются укрупненные «блоки», затем анализируются отношения внутри этих «блоков». Примером такого приема может служить прием замены переменной.

5. Прием использования аналогии.

Автор распределяет выделенные приемы по трем этапам решения творческих задач:

1. Анализ данных, условий и их соотношений. Появление общей идеи. Операции сопоставляются с требованиями.

2. Специализация и конкретизация общей гипотезы (идеи). Операции сопоставляются с общей идеей (в отличие от сопоставления с требованиями на 1-ом этапе).

3. Нахождение конечного результата (результат сопоставляется с требованиями).

Ю.Н. Кулюткин, при решения творческой задачи, на каждом этапе, предлагает использовать прием сопоставления. Сутью же решения является временный отказ от ограничивающих условий с последующим их наращиванием.

Из выше приведенного можно сделать вывод, что количество приемов, предлагаемые авторами, большое количество, а систематизируются они редко. Однако по своей сути приемы можно объединить в группы, и этих групп окажется не так много. Часто приемы имеют лишь разное название и не отличаются по соержанию.

И.И. Ильясов разобрал огромное количество приемов, выделил эдентичные по своему содержанию и сгруппировал их в семейства. «Таким образом, - пишет И.И. Ильясов, - действительно разных по содержанию приемов всего насчитывается немногим более тридцати» [19]. Итак, система эвристических приемов по И.И. Ильясову имеет вид.

Тождественными по содержанию являются такие приемы, как:

─ освобождение от излишнего представления, обобщение цели, обобщение задачи, гипостазирование свойства, установление общей схемы условий, освобождение данных от привходящих обстоятельств, пренебрежение некоторыми условиями, переформулирование по входящей линии, устранение лишних элементов, редукция лишних элементов и отношений, планирование по Саймону, использование аналогичной общей задачи и некоторые другие;

─ конкретизация задачи, формирование частной вспомогательной задачи, специализация, переформулирование по нисходящей линии, использование аналогичной конкретной задачи;

─ формулирование обратной задачи и доказательство от противного, противоположное движение;

─ исключение из структуры, устранение компонентов, изоляция;

─ критика очевидных решений и блокирование очевидных репродуктивных гипотез;

─ поиск привнесенных условий и преодоление фиксированности;

─ движение от конца к началу, постановка промежуточных задач, выведение следствий из условий, функциональный анализ (по Саймону), логическая редукция;

─ сближение данных и цели, устранение различий между условиями и целями, выражение в одном языке, поиск тождественного в различном;

─ черчение фигур, перекодирование текста в схему, рисование изображений, наглядное представление явлений, моделирование;

─ перенос исходных признаков и использование сходных задач;

─ привлечение всех известных знаний о возможных видах явлений задачи и их характеристиках, морфологический анализ, установление типов решения проблем, рассмотрение с разных возможных сторон, выбор многих возможных начал;

─ анализ данных и цели, анализ условий, явное представление всех фактов;

─ анализ конфликта, осознание конфликта, фиксация противоречия, образование проблемного комплекса, формулирование идеального общего результата;

─ запрет критики, мозговой штурм, выдвижение любых идей;

─ переструктурирование и перегруппировка.

Каждой группе приемов можно дать одно название, так как приемы одной группы это всего лишь разные названия одного и того же по своей сути приема. Поэтому дальше мы будем пользоваться следующими названиями групп:

─ обобщение задачи;

─ конкретизация задачи;

─ формулирование обратной задачи;

─ исключение из структуры;

─ критика очевидных решений;

─ поиск привнесенных условий;

─ движение от конца к началу;

─ сближение данных и цели;

─ перекодирование текста в модель;

─ использование сходных задач;

─ рассмотрение с различных сторон;

─ анализ условий;

─ анализ конфликта;

─ выдвижение любых идей;

─ переструктурирование.

─ включение в другую структуру,

─ включение в деятельность,

─ введение дополнительных элементов или отношений,

─ деление задачи на части,

─ выделение доминирующих целей,

─ подведение под логические категории,

─ подведение под диалектические категории,

─ резонанс,

─ замена терминов определениями,

─ выдвижение противоположных гипотез,

─ анализ оснований гипотез,

─ оценка достоинств и недостатков гипотез,

─ перерыв в решении задач, отдых,

─ параллельное решение нескольких задач,

─ вживание в образ явлений задачи,

─ регуляция уровня уверенности в себе,

─ движение от общих идей к частным,

─ символическая запись условий,

─ определение области и поиска неизвестного.

Как мы видим, различных по своей сути приемов не так много, а если еще более обобщить приемы, то получаем вполне действующую систему эвристических приемов для обучения решению задач.

Лишь тридцать с небольшим приемов разнятся между собой по содержанию. Объединение приемов в семейства, дает возможность систематизации и лучшее понимание их особенностей и связей.

Сделав более детальный разбор выделенных тридцати двух приемов, приходим к установлению следующих 11 семейств приемов:

1. Анализ условий задачи, анализ данных, анализ требований, анализ конфликта.

2. Доопределения, развертывание определений явлений задачи, движение от конца к началу, подведение под логические категории, подведение под диалектические категории, сближение данных и цели, резонанс.

3. Изменение уровня обобщенности задачи, обобщение задачи, использование известной общей задачи, конкретизация задачи, использование известной конкретной задачи.

4. Включение в новые связи, подведение под компоненты деятельности, включение в другую неизвестную структуру, включение в другую известную структуру, введение дополнительных элементов или отношений (неизвестных и известных), переструктурирование, деление задачи на части.

5. Анализ допущений, выделение доминирующих идей, критика очевидных решений, поиск лишних условий.

6. Моделирование, перекодирование текста в схему (модель), символическая запись.

7. Выдвижение любых гипотез, выдвижение маловероятных гипотез, выдвижение противоположных гипотез.

8. Обоснование принятия и отвержения гипотез, обоснование выдвижения гипотез, анализ достоинств и недостатков гипотез.

9. Переключение в другие проблемы, параллельное решение нескольких задач, перерыв в решении задач.

10. Вживание в образ явлений задачи, принятие роли объекта или процесса задачи, «метод демонов» (по Максвеллу).

11. Регулирование уровня уверенности в себе, повышение уровня уверенности в себе, понижение уровня уверенности в себе.

«В этой системе, так или иначе, представлены почти все значимые семейства эвристических приемов, известные на сегодняшний день», считает И.И. Ильясов[19].

ГЛАВА 2. Методические особенности формирования эвристических приёмов на уроках математики в 5-6-х классах

2.1 Пути и условия организации эвристического обучения в школе

Основным средством развития творческого мышления и математических способностей являются математические задачи. Не случайно известный математик и методист Д. Пойа пишет: «Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности».

Задачи находящиеся в современных школьных учебниках, как правило ограничены одной темой, и это одна из главных причин, не эффективного использования учебного времени на уроках математики. Для решения подобных задач от ученика требуются знания и умений только по одному вопросу и не предполагаются пересечения с другими темами. Значение такой задачи заканчивается после прохождения определенной темы, а решение подсказывается названием главы. Такие задачи являются лишь наглядным пособием для разъяснения смысла теоритического материала, а при решении задач, в которых надо знать не одну тему, у школьников вызывают затруднения.

Кулюткин Ю.К., в своей книге «Эвристические методы в структуре решений» пишет: “К сожалению, в практике обучения математике решение задач чаще всего рассматривается лишь как средство сознательного усвоения школьниками программного материала. И даже задачи повышенной трудности специальных сборников, предназначенных для внеклассной работы, в основном имеют целью закрепление умений и навыков учащихся в решении стандартных задач, задач определенного типа. А между тем функции задач очень разнообразны: обучающие, развивающие, воспитывающие, контролирующие” [7].

Хотя каждая задача служит развитию каких-то определенных умений, главной целью все таки остается развитие творческого умения, увлеченность математикой.

«Мы такие задачи не решали»,- можно услышать от детей, когда они встречают не стандартную задачу. Это как раз результат обучения, где используются только стандартные задачи. Стандартные задачи, конечно, полезны и необходимы, но достичь творческого мышления используя только задачи стандартного типа невозможно, дети не получат умения самостоятельно решать не только математические задачи, но это и не даст ни какой мотивации решать жизненные проблемы самостоятельно.

Бесспорно, задачи которые вырабатывают определенные математические навыки, умения – необходимы (задачи иллюстративного характера, тренировочные упражнения, выполняемые по образцу). Но также необходимы и задачи, которые вырабатывают самостоятельность, интерес к изучению математике. Необходимы специальные упражнения направленные на обучение и овладение общим приемам решения проблем. наблюдательности, пользование аналогией, индукцией, сравнениями, выдвижению соответствующих выводов, но в учебниках очень мало задач такого типа.

Поэтому учитель может исходить из сложившейся ситуации и сам должен использовать творческое мышление, например, переформулировать задачу:

Задача. «Докажите, что для того, чтобы найти квадрат двузначного числа, оканчивающегося цифрой 5 и имеющего п десятков достаточно число десятков п умножить на п + 1 и к результату приписать 25» , конечно эта стандартная задача имеет свою ценность: дети изучают правила возведения в квадрат двузначных чисел, оканчивающихся на 5. Но эта задача повысит свою ценность, если ее сформулировать так: «Найдите и обоснуйте правило возведения в квадрат двузначных чисел, оканчивающихся цифрой 5».

Очень познавательна, в этой связи, книга американского педагога У. Сойера «Прелюдия к математике» [17]. «Для всех математиков – характерна дерзость ума. Математик не любит, когда ему о чем-нибудь рассказывают, он сам хочет дойти до всего. Эта «дерзость ума» особенно сильно проявляется у детей. Если вы, например, преподаете геометрию 9-10-летним ребятам и рассказываете, что никто еще не смог разделить угол на три равные части при помощи линейки и циркуля, вы непременно увидите, что один - два мальчика останутся после уроков и будут пытаться найти решение. То обстоятельство, что в течение 2000 лет никто не решил эту задачу, не помешает им надеяться, что они смогут это сделать в течение часового перерыва на обед. Это, конечно, не очень скромно, но и не свидетельствует об их самонадеянности. Они просто готовы принять любой вызов. А ведь в действительности уже доказано, что невозможно разделить угол на три равные части при помощи линейки и циркуля. Их попытка найти решение - того же рода, что попытка представить «корень из двух» в виде рациональной дроби p/q. Хороший ученик всегда старается забежать вперед. Если вы ему объясните, как решать квадратное уравнение дополнением до полного квадрата, он непременно захочет узнать, можно ли решить кубическое уравнение дополнением до полного куба. Вот это желание исследовать является отличительной чертой математика. Это одна из сил, содействующих росту математика. Математик получает удовольствие от знаний, которыми он уже овладел, и всегда стремится к новым знаниям».

Математика всегда интересует закономерность, так как это самая стабильная характеристика нашего ежемнгновенно меняющегося мира. В одну и туже реку не возможно войти дважды.

Когда дети начинают учить таблицу умножения, легче всего они запоминают умножение на 2 и на 5. Так как при умножении на 2 получаются только четные числа, а при умножении на 5 все еще проще, такие числа оканчиваются на 5 или 0. И дети эти закономерности находят сами, упрощая тем самым себе задачу. Дети любят находить закономерности во всем.

2.2 Формирования эвристических приёмов при обучении математике школьников 5-6-х классов

«... Задачи, которые приходится решать человеку, могут быть такими, что их можно решить путем простого воспоминания и применения знаний о способе их решения. В этом случае задача является типовой, стандартной... Если же формула решающему неизвестна, то задача приобретает уже другой характер. Сначала надо найти нужную формулу. Поиск может осуществляться либо путем выведения из каких-то других общих знаний, либо путем угадывания, пробами и ошибками и т.п. В первом случае задача является вводной, во втором - творческой…» Так И.И. Ильясов характеризует типовые, выводные и творческие задачи.[19]

Многие авторы подчеркивают, что опыт эвристической деятельности можно передать только с помощью эвристических задач. Сущность таких задач состоит в том, что на основе некоторых данных ученик должен разрешить проблему.

Задачи, направленные на развитие творческого мышления у учеников 5-6 классов, разделяют на пять групп. В каждой группе находятся задачи направленные на формирование определенного эвристического приема. И приемы, которые использовались в первых группах разрешено использовать и дальше.

I группа - задачи на формирование эвристического приёма выдвижения гипотез.

II группа - задачи на формирование эвристического приёма моделирования с помощью прямой, таблиц или графов.

III группа - задачи на формирование эвристического приёма конкретизации условия.

IV группа - задачи на формирование эвристического приёма переструктурирования условия задачи.

V группа - задачи на формирование эвристического приёма разбиения задачи на части.

Таким образом школьники последовательно знакомятся с эвристическими приемами.

Приемы работы с гипотезами (выдвижения любых гипотез, их проверка, анализ).

П.Я. Гальперин и В.Л. Данилова [10] подробно разобрали этот прием в своих трудах. «Его особенность составляли «бухгалтерия догадок» и систематическая их проверка; каждая догадка немедленно записывалась, потом все они проверялись, строго по очереди, и не только по результату, но и по источнику и по общему значению в системе условий». Если учитель дает детям задачу на смекалку, то те начинают, соревнуясь, высказывать беспорядочно свои гипотезы, не доведя полностью проверку до конца перескакивают на другие, потом опять возвращаются к старым и т.д.. На этом этапе есть возможность выработать системность мышления школьников, фиксируя каждую(даже самую абсурдную гипотезу) на доске и после в строгом порядке, как записано на доске, делать полную проверку каждой гипотезы, кроме того, это ускоряет и повышает эффективность поиска.

Давайте рассмотрим как это работает на практике.

Задача. Крестьянин должен был переправить через реку лису, зайца и морковку. За один рейс он мог переправится сам и перевезти или только лису, или только зайца, или только морковку. Но если оставить лису с зайцем без человека, то лиса съест зайца; если оставить зайца с морковкой, то заяц съест морковку. Сможет ли крестьянин, если да, то как, переправить свой груз через реку.

Решение. 1 – ый этап – анализируем условия задачи: что дано в задаче?, какую проблему требуется решить?», можно ли перевезти всех за один рейс?.

2 – этап – поиск решения.

Преподаватель: Кого переправим первым?

Дети на перебой начинают высказывать гипотезы. Учитель по порядку записывает все гипотезы на доске.

- морковку,

-лису,

-зайца

Преподаватель: Все возможные гипотезы записаны на доске. Теперь начнем проверку каждой из них. Первая гипотеза: Может ли первой быть морковка?

Дети: Нет, т.к. лиса съест зайца.

Преподаватель: Значит, первая гипотеза не верна. Вычеркиваем ее. Второе предложение: может ли первой быть лиса?

Дети: Нет, т.к. Заяц без присмотра съест морковку.

Преподаватель: Вычеркиваем втору гипотезу. Проверяем третью гипотезу : может ли первым быть заяц?

Дети: Может, лиса не съест морковку.

Преподаватель: В итоге, верна третья гипотеза Первым пойдет заяц. Что же дальше? Что будем перевозить вторым рейсом? Выпишем все предложения.

- морковку,

-лису.

Далее тем же способом проверяются эти гипотезы. О вычеркнутых гипотезах забываем. Когда, в результате, проверки обнаруживается, что ни одна из гипотез не подходит, сыпется множество предложений, в которых дети пытаются обойти проблему. Все замолкают, из-за не возможности решить задачу. И здесь можно использовать такой прием, как анализ отвергнутых гипотез.

Преподаватель: У нас было два предложения, но оба они не верны. Что же в этих случаях нам мешало? Давайте обсудим.

Дети: В первом случае кролик съест привезенную морковку. Морковку нельзя вести. Не было бы кролика, то морковку можно было бы везти.

Во второй гипотезе лиса съест кролика, поэтому лису нельзя привозить. Не было кролика, тогда бы все получилось.

Преподаватель: Кролик в обоих случаях нам мешает. Что делать?

Дети: Увезти кролика.

Преподаватель: У нас родилась еще одна гипотеза увезти кролика. Проверим ее.

Проверяя находим искомое решение проблемы.

Дале мы предлагаем еще ряд подобных задач, решаемых с помощью того же приема, по аналогии с выше представленным.

Задача 1. Сколько словарей необходимо переводчику, чтобы он мог переводить с любого из четырех языков – русского, английского, немецкого, французского – на любой другой из этих языков.

Задача 2. Путешественник попал в плен кровожадным дикарям. По законам племени, всякого иностранца спрашивают о цели визита. Если он при этом скажет правду - его съедят, а если солжет - утопят в море. Как путешественнику остаться в живых?

Приемы моделирования.

По определению Л.М. Фридмана [18] «моделью некоторого объекта А (оригинала, прототипа) называется объект В, в каком-то отношении подобный (аналогичный) оригиналу А, но отличающийся от него. Целью построения модели является замена А в некотором мысленном (воображаемом) или реальном действии, исходя из того, что В более удобно для этого действия в данных условиях». Мы будем использовать модели - заместители. А моделированием Л.М. Фридман называет «особую деятельность по построению или выбору модели...» [18].

Учащиеся не осознают, что уравнение, геометрические фигуры, число, функция и т.д. – все это математические модели. Поэтому учителю необходимо дать четкое понимание таких понятий как модели и моделирование, их сути и назначение. Дети должны понять необходимость строить модели, сами изучать какие-то явления с помощью моделирования. Это понимание сделает работу учащихся осмысленной и наиболее продуктивной. В 5-6-х классах обучение моделированию, лучше всего проводить на таких доступных и понятных детям примерах, как таблицы, схемы, графы.

1. Прием моделирования на полупрямой.

Если в задаче требуется установить отношения между множеством элементов, то подобные задачи лучше всего решать используя полупрямую.

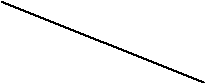
Задача. На дистанцию 10 км стартовало 4 лыжника: Шубин, Иванов, Петров и Сидоров. Об их финише нам известно только то, что Сидоров пришел раньше Шубина, но не был первым. Иванов пришел последним. В какой последовательности финишировали лыжники.

Решение. Модель данной задачи будем строить на “ полупрямой времени”. Лыжников пометим кругами, и внутри кругов будем ставить первые буквы их фамилий.

Сидоров пришел раньше Шубина (рис.2).

Рисунок 2

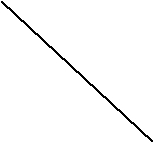
Иванов пришел последним (Рис.3)

Рисунок 3

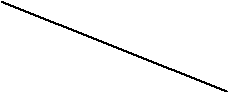
И остается Петров, о котором ничего не сказано, но ни один из трех остальных не был первым. Следовательно это был Петров (Рис.4).

Рисунок 4

1. Прием моделирования с помощью таблицы.

Если задача имеет более двух множеств, между которыми надо выяснить отношения, для этого можно использовать таблицы. Поля таблицы здесь - декартово произведение этих множеств.

Задача. В одном из Питерских вузов на разных курсах учатся четыре студента. Определить фамилию, имя, курс, на котором учится каждый студент, если известно, что:

1) Дмитрий прошлую летнюю сессию сдал на отлично;

2) Алексей должен был летом ехать на практику в Магадан, а Куропаткин собирался поехать домой в Екатеринбург;

3) Александр был курсом старше Андрея;

4) Дмитрий и Конев коренные питерцы;

5) Ковалев в прошлом учебном году окончил школу и поступил на тот же факультет, на котором учился Зубов;

6) Дмитрий иногда пользовался прошлогодними конспектами Алексея.

Решение. Анализируем задачу и выделяем три множества: имена, фамилии, курс. В таблице будут отражаться отношения между именем и курсом, между курсом и фамилией и именем и фамилией.

Следующим шагом уберем невозможные пары отношений.

Таблица 2

		Фамилия					Курс
		Зубов	Ковалев	Куропаткин	Конев	I		II	III	IV
Имя	Дмитрий	+	-	-	-	-		-	+	-
	Алексей	-	-	-	+	-		-	-	+
	Александр	-	-	+	-	-		+	-	-
	Андрей	-	+	-	-	+		-	-	-
Курс	I	-	+	-	-
	II	-	-	+	-
	III	+	-	-	-
	IV	-	-	-	+

Начнем отмечать истинные отношения знаком “+”, ложные знаком “-”

Дмитрий прошлую сессию сдал на отлично, следовательно, Дмитрий не на 1-ом курсе – в клеточке (Дмитрий.,1) ставим “-”.

Алексей летом улетает в Магадан, а Куропаткин в Екатеренбург, значит фамилия Алексея не Куропаткин - в клеточке (Алексей, Куропаткин) ставим “-”.

Александр старше Андрея на один курс, следовательно, Александр учится не на 1-ом курсе – в клеточке (Александр, 1) ставим “-”.

Дмитрий и Конев - коренные питерцы, значит фамилия Дмитрия не Конев - в клеточке (Дмитрий., Конев.) ставим “-”.

Ковалев окончил школу в прошлом году, следовательно он – на первом курсе - в клеточке (Ковалев., 1) ставим знак “+”. Ни Зубов, ни Куропаткин, ни Конев значит не учатся на 1-ом курсе - здесь ставим “-”.

Дмитрий использует прошлогодние конспекты Алексея, то значит Алексей на курс старше Дмитрия, но, следовательно, Дмитрий не на первом курсе, и Алексей учится не на 1-ом и не на 2-ом курсах - в клеточках (Алексей, 1) и (Алексей, 2) ставим “-”.

Куропаткин из Магадана, а Дмитрий коренной питерец, следовательно, Дмитрий не Куропаткин - в клеточке (Дмитрий, Куропаткин) ставим “-”. Анализируя таблицу, видим, что на первом курсе не учится ни Дмитрий, ни Алексей, ни Александр, значит, на первом курсе учится Андрей – в клеточке (Андрей, 1)можно поставить знак “+”а в клеточках (Андрей, 2), (Андрей, 3) и (Андрей, 4) ставим “-”. Также на первом курсе учится Ковалев, следовательно Андрей имеет фамилию Ковалев - (Анддрей, Ковалев) ставим знак “+”. Из этого следует, что Анрей - ни Куропаткин, ни Зубов, ни Конев, ставим “-”, а Ковалевым не могут быть ни Дмитрий, ни Алексей, ни Александр – ставим “-”.

Смотрим на столбец «Куропаткин»: замечаем, что в полях Дмитрий, Александр, Андрей стоит знак “-”, следовательно, только Александр является Куропаткиным, в клеточке (Александр, Куропаткин) ставим знак “+”. Из этого следует – имя Конева и Зубова не Александр - здесь ставим “-”.

Просматриваем столбец «Конев»: ни Дмитрий, ни Александр, ни Андрей не являются Коневым, значит Алексей носит фамилию Конев –в клеточке (Алексей, Конев) ставим знак “+”. Алексей не может быть Зубовым - “-”. Видно, что только Дмитрий - не Зубов.

Андрей Ковалев учится на первом курсе, Александр Куропаткин курсом старше Андрея, следовательно, Александр Куропаткин учится на 2-ом курсе – отметим “+”.

Алексей Конев курсом старше Зубова Дмитрия, Зубов Дмитрий учится на третьем курсе, а Алексей Конев - на четвертом. Задача решена. Ответ представлен в таблице.

3. Прием моделирования с помощью графов.

Предыдущую задачу можно решить также моделированием с помощью графов. В этой модели элементы различных множеств обозначают точками, соответствия между ними – отрезками. Пунктирные линии обозначают известные отсутствия соотношений.

Задача. Николай, Борис и Никита преподают различные предметы (литература, математика, музыка) в школах Омска, Пскова и Читы. О них известно:

1) Николай работает не в Омске, а Борис - не в Чите;

2) Житель Омска преподает музыку;

3) тот, кто работает в Чите, преподает литературу;

4) Борис и Никита преподают не математику;

Какой предмет, и в каком городе преподает каждый?

Решение: Выделяем 3 множества: учебные предметы, города, учителя. Каждое множество содержит по три элемента. Обозначим их надписями - вершины графов (рис. 5).

Николай

Никита

Борис

Литература

Омск

Математика

Псков

Музыка

Чита

Рисунок 5. Решение задач с помощью графов.

Рисунок 5

Теперь, если есть соответствие между элементами, будем соединять их жирными черными линиями, если нет – тонкими голубыми.

Далее, находим три треугольника, стороны, которых состоят из черных жирных линий.

Принимая во внимание условие 1, проводим тонкие голубые линии между надписями Николай и Омск, Борис и Чита.

Соединяем Омск и Музыка (условие 2), Чита и Литература, черной жирной линией (условие 3).

Надписи Борис и математика, Никита и математика соединяем тонкой голубой линией (условие 4).

Из условия 4 понятно, что математику преподает Николай (соединяем черной жирной линией).

Учитель литературы живет в Чите, а учитель музыки в Омске, Математик в Пскове.

Николай соединен черной жирной линией с Псковом и Математикой, следовательно, можно соединить математику и Псков черной жирной линией. Один треугольник построен.

Борис не живет в Пскове (это место жительства Николая) и не живет в Чите (по условию) – соединяем тонкой голубой линией. Получается Борис живет в Омске (соответственно соединяем). Но тот кто живет в Омске преподает музыку (черная жирная линия). Образовался треугольник Борис, Омск, музыка. Готов второй треугольник.

И остались у нас три надписи – это третий треугольник (Никита, Чита, Литература.

Задача решена.

1. Моделирования с помощью блок-схемы.

Блок-схемой (прямоугольником) выделяется каждый шаг в рассуждении при решении задачи.

Задача. На некотором острове отдельными селениями живут «правдолюбы» и «шутники». «Правдолюбы» всегда говорят только правду, а «шутники» постоянно шутят, а поэтому всегда лгут. Жители одного племени бывают в селении другого племени, и наоборот. В одно из селений попал путешественник, но не знает в какое. Доказать, что путешественнику достаточно первому встречному задать вопрос: «Вы местный?», чтобы по ответу определить, в селении какого племени он находится.

Решение. У путешественника только два варианта: он в селении “правдолюбов” или селении “шутников”. В любой из деревень он может встретить жителя соседней деревни. Представим это блок-схемой (рис.6).

Путешественник

Деревня шутнков

Деревня правдолюбов

шутник

шутник

Правдолюб

Правдолюб

нет

нет

да

да

Рисунок 6. Решение задач с помощью блок-схемы.

Проанализировав блок-схему, видим, что ответ “да” возможен только в селении правдолюбов, а ответ “нет” – только в деревне шутников.

Блок-схема позволяет их представить наглядно и заметить, что положительный ответ в любом случае возможен только в селении «правдолюбов», а ответ «нет» - только в селении «шутников».

На этих примерах моделей (полупрямая с точками, таблица, граф, блок-схема) отчетливо видна «главная эвристическая функция» моделей (Д.Б. Богоявленская [6] – порождающая, т.е. с модели «как бы считывается тот или иной принцип решения (идея, гипотеза, концепция)».

Задача 1. В четырех теплицах находится 264 растения. Когда из первой теплицы взяли 16 растений, со второй пересадили в третью 15, а в четвертую посадили 12 растений, то во всех теплицах растений оказалось поровну. Сколько растений было в каждой теплице первоначально?

Задача 2. Жители города А говорят только правду, жители города Б – только ложь, а жители города В – попеременно правду и ложь (то есть из двух утверждений, высказанных ими, одно истинно, а другое ложное).

Дежурному по пожарной части по телефону сообщили:

- У нас пожар, приезжайте скорее!

- Где? – спросил дежурный.

- В городе В, - ответили ему.

Куда должна ехать пожарная машина?

Прием конкретизации задачи.

Прием конкретизации задачи «состоит в нахождении более частной задачи путем введения дополнительных видовых свойств явлений и конкретных примеров общей задачи» (И.И. Ильясов [19]).

Задача. Три биатлониста - Боря, Иван и Дима - в соревнованиях по биатлону заняли три первых места. Когда же мальчиков спросили, кто из них занял первое место, они ответили так:

Боря: Я занял первое место.

Иван: Я занял не первое место.

Дима: Я занял не третье место, однако, вы учтите, что один из ответов моих друзей правильный, а другой - неправильный.

Кто занял в соревнованиях первое место, если Димин ответ во всем правдив?

Решение. Ответ Димы правдив, он занял не третье место, а второе или первое. Боря утверждает, что занял первое место. Говорит он правду или нет - не известно. Конкретизируем задачу: допустим, Боря говорит правду. Он занял первое место. Тогда, Иван сказал неправду. И он занял первое место. Но получается, и Боря и Иван заняли первое место, чего не может быть. Конкретизируем по-другому: Боря сказала неправду. Он не занимал первого места, а занял второе или третье. Если Боря сказал не правду, тогда правду сказал Иван. Т.е. первого места он не занимал. Получается ни Боря , ни Иван не занимали первого места. Остается только Дима кандидат на первое место.

Ответ: первое место занял Дима.

Задача 1. Вася, Леша, Андрей, Тимур – пили чай в одинаковых кружках. И разбили одну кружку. Когда их спросили, кто это сделал. Были получены следующие ответы:

Леша: «Это сделал Андрей или Тимур.

Тимур: «Я этого не делал».

Вася: «Это сделал Андрей»

Миша: «Вася ошибается»

Дядя Петя сказал: «Троих из них я знаю очень хорошо, и они говорят правду. А четвертого я знаю плохо».

Вопрос: «Кто разбил чашку?. И кого дядя Петя знает плохо?»

Задача2. Четыре гимнастки – Даша, Катя, Юля, Соня в соревнованиях по гимнастике заняли первые четыре места. Отвечая на вопрос, кто занял какое место, они сказали:

1) Юля заняла первое место, Катя - второе

2) Юля - второе, Соня - третье

3) Даша - второе, Соня – четвертое.

Одна часть каждого ответа правдива, другая ложна. Какое место заняла каждая из гимнасток?

Задача 3. Одна из трех сестер пролила на палас варенье.

- Кто это сделал? – спросил папа.

- Юля не пачкала палас, - сказала Даша. – Пролила варенье Катя.

- Это Юля сделала, - сказала Катя. – А Даша не пачкала палас.

- Я знаю, что Катя не могла это сделать. А меня сегодня не было дома, - сказала Юля

Известно, что двое девочек говорят, а одна солгала. Кто пролил варенье?

Прием переструктурирования задачи.

«Изменение расположения уже имеющихся элементов как путем извлечения соотношений между ними в новой диспозиции, так и перестановкой или перегруппировкой этих элементов», по словам И.И. Ильясова [19] , заключается прием переструктурирования.

Рассмотрим пример.

Задача.

Акробат и собачонка

Весят два пустых бочонка.

Шустрый пес без акробата

Весит два мотка шпагата.

А с одним мотком ягненок

Весит, видите, бочонок.

Сколько весит акробат

В пересчете на ягнят?

Решение. Сделаем рисунок к задач, где буква А – акробат, буква С – собачонка, буква Я – ягненок. Ш – шпагат, Б – бочонок.(рис. 8)

А+С=Б+Б

С=Ш+Ш

Я+Ш=Б

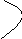
А+С=Я+Ш+Я+Ш

Рисунок 8. Пример приема переструктурирования.

Третье равенство переставим в первое условие, заменив каждый бочонок ягненком с мотком шпагата.

В равенство А+С=Я+Ш +Я+ Ш подставим элементы второго условия, т.е. заменим два мотка шпагата собачонкой.

А+С=2Я+С

Итак, А = 2Я, акробат весит столько же, сколько и два ягненка. Задача решена.

Задача 1. У Леши, Симы и Пети вместе 100 рублей. У Вовы, Симы и Пети – 90 рулей. У Вовы, Леши, Пети – 95 рублей. У Вовы, Леши, Симы – 80 рублей. Сколько денег у каждого?

Задача 2. Катя и Саша вместе весят 92 кг, Катя и Вика весят 79 кг, Саша и Вика весят 84 кг, Сколько весят вместе Катя, Саша и Вика?

Задача 3. Сколько людей в команде по легкой атлетике, если средний возраст членов команды вместе с тренером 25 лет, тренеру 45 лет, а средний возраст команды без тренера 23 года?

Задача 4. Крестьянин, зная, что коза стоит в четверо дороже кота, поросенок в четверо дороже козы, взял с собой на ярмарку 40 рубле й. И на все деньги купил кота, две козы, и поросёнка. Сколько стоит каждое животное?

Прием разбиения задачи на части.

Иногда из задачи можно выделить отдельные задачи (подзадачи), и решить их по очереди.

Задача. Заспорили три мудреца о том, кто из них самый мудрый. Наконец, они обратились к судье, славившемуся своей мудростью. «Скажи нам, справедливейший из судей, кто из нас самый мудрый?»

Задумался судья, а потом и говорит: «Вот перед вами лежат 5 тюбетеек: 3 из красного бархата, а 2 - из черного. Сейчас вам завяжут глаза и наденут тюбетейки на головы. Когда повязки с ваших глаз снимут, самый мудрый из вас скажет, какая тюбетейка у него на голове».

Так и сделали. Сняли повязки с глаз: видит каждый перед собой красные тюбетейки на головах товарищей, а какая на своей голове - не знает. Наконец, один мудрец сказал: «О справедливейший из судей! Ты велел надеть на меня красную тюбетейку».

«Вот ты и есть самый мудрый из вас троих» - решил судья.

Как мудрец догадался, что на нем красная тюбетейка?

Решение. Так как всего было 5 тюбетеек:

3 красные и 2 черные, то возможны три различных варианта:

а) на трех мудрецов надели 2 черные и 1 красную тюбетейку;

б) на трех мудрецов надели 1 черную и 2 красные тюбетейки;

в) на трех мудрецов надели 3 красные тюбетейки.

Каждый случай можно рассмотреть отдельно. Причем любая предыдущая подзадача помогает разобраться в последующей подзадаче.

В случае а) кто-то из мудрецов увидел бы или 2 черные тюбетейки (если на нем самом была красная), или 1 черную (если на нем была черная). А это противоречит условию, где сказано, что каждый увидел только красные тюбетейки.

В случае б) любой из собратьев обладателя черной тюбетейки увидел бы ее. А это тоже противоречит условию.

Остается случай в). К нему можно прийти без всяких дополнительных рассуждений.

Но тот, кто догадался о цвете своей тюбетейки, не знал, что каждый из спорщиков увидел только красные тюбетейки. Он мог предполагать, что на нем - черная. Но ему подсказало верный ответ молчание товарищей. Если бы кто-то из них увидел два черных головных убора, то сразу бы дал верный ответ относительно себя. Но молчание обоих свидетельствовало о том, что любой из них сомневался относительно того, какая тюбетейка у него на голове. А это могло быть только тогда, когда каждый увидел две красные тюбетейки.

Задача 1. Утомившись от споров и летнего зноя, три древнегреческих философа прилегли немного отдохнуть под деревом сада Академии и уснули. Пока они спали, шутники испачкали углём их лбы. Проснувшись и взглянув друг на друга, все пришли в весёлое настроение и стали смеяться, но это никого не тревожило, так как каждому казалось естественным, что двое других смеются друг над другом. Внезапно один из мудрецов перестал смеяться. Так как он сообразил, что его собственный лоб также запачкан. Как он рассуждал?

Задача 2. У падишаха было трое мудрецов, но мудрецы всегда давали ему разные, часто противоречивые советы. Тогда падишах решил узнать, кто из этих мудрецов самый умный, чтобы прислушиваться к его советам. Созвав своих мудрецов, падишах показал им 5 тюбетеек: 3 чёрные и 2 белые. Завязав каждому мудрецу глаза, падишах велел надеть им на головы тюбетейки:

1) одному чёрную, двум другим белые,

2) двум чёрные, одному белую;

3) всем трём по чёрной.

Каждый мудрец видит только тюбетейки у своих товарищей, но не видит своей. Кто из мудрецов может сказать, какого цвета на нём тюбетейка в каждом из трёх случаев? Как будут рассуждать мудрецы? Какой случай: 1), 2) или 3) падишах должен был использовать для определения наимудрейшего?

2.3 Эвристический урок по математике

Урок №1. Признаки делимости на 2, на 5 и на 10 (6-й класс)

Цель урока:

 ОБУЧАЮЩИЕ: ознакомить учащихся с признаками делимости на 2, на 5 и на 10, научить применять признаки к решению задач.;

 РАЗВИВАЮЩИЕ: развить у учащихся логическое мышление, творческое мышление, развить грамотную устную речь;

 ВОСПИТЫВАЮЩИЕ: воспитывать уважение к одноклассникам;

Задачи урока: сформулировать признаки делимости, научить применять признаки к решению задач.

Инструменты: раздаточный материал, доска, учебник.

Учитель: Здравствуйте дети, садитесь. Давайте сейчас выполним не большую самостоятельную работу, а после вместе сформулируем и запишем тему урока. Дается самостоятельная работа.

Самостоятельная работа

1. Выпишите отдельно (под буквами а), б), в) ) какие из чисел 123, 234, 4567, 2310, 455, 34, 5430, 244, 876, 9085, 13 делятся без остатка на:

а) на2; б) на 5; в)на 10.

Дети самостоятельно находят такие числа и выписывают их в группы.

а) 234, 2310, 34, 5430, 244, 876;

б) 2310, 455, 5430, 9085;

в) 2310, 5430

Учитель: А теперь давайте посмотрим внимательно на группу а). Что вы можете сказать об этой группе.

Дети смотря, думают.

Учитель: Не большая подсказка. Какие числа называются четными.

Дети: Числа, которые делятся на 2. Получается в группе а) четные числа.

Учитель: Правильно. Молодцы. Давайте еще раз посмотрим и попробуем ответить на вопрос: «Какой цифрой заканчивается четное число»

После некоторой паузы.

Дети: Цифрой которая делится на 2.

Учитель: Молодцы. Давайте рассмотрим и проанализируем группу б). Что можно сказать об этой группе?

Дети: Эти числа заканчиваются на «0» и на «5».

Учитель: Значит….

Дети: На «5» делятся числа, которые заканчиваются на «0» и на «5».

Учитель: Теперь рассмотрим группу в).

Теперь дети, поняв ход рассуждений, отвечают сразу.

Дети: На «10» делятся числа, которые заканчиваются цифрой «0».

Учитель: Молодцы. Запишем тему урока. Как она будет, по вашему, звучать?

Дети: Числа, которые делятся на 2, 5 и 10.

Учитель: Почти так. Только хорошо бы еще добавить слово «признаки».

Дети: Признаки делимости чисел на 2, 5, 10.

Учитель: Записываем. И давайте грамотно сформулируем и запишем сами признаки. Как будет звучать признак делимости чисел на 2.

Дети: Числа, которые заканчиваются четной цифрой, делятся на 2 без остатка.

Учитель: Какие мы все молодцы. Давайте сформулируем и запишем теперь еще два признака.

Дети: Числа, которые оканчиваются цифрами 5 и 0, делятся на 5 без остатка. И последний признак. Числа, которые оканчиваются цифрой 0, делятся на 10 без остатка.

Учитель: Теперь закрепим, то что мы сегодня узнали. Я буду писать число, оставлять последнюю цифру не записанной, говорить условие, а вы будете говорить какую последнюю цифру, я должен буду записать. И так.

Учитель записывает на доске число 453*.

Учитель: Какую цифру вместо звездочки я должен записать, чтобы полученное число делилось на 5 и не делилось на 10.

Дети: Цифру 5.

Учитель: Делилось на 2 и не делилось на 10.

Дети: Цифру 2.

Учитель: Может быть, есть еще какая-та цифра, которую я могу записать вместо звездочки.

Дети: 4, 6, 8.

Учитель: Умницы. Делилось на 2, на 5 и на 10.

Дети: Цифра 0

Учитель: Не делилось на 2, на 5 и на 10

Дети начинают перечислять: 1, 3,7, 9.

Учитель: Верно ли утверждение: Если число делится на 5, то оно делится на 10

Дети: Неверно. 25 делится на 5, но не делится на 10.

Учитель: Если число делится на 5, то оно делится на2

Дети: Нет. 25 делится на 5, но не делится на 10.

Учитель: Если число делится на 2, то оно делится на 5

Дети: Нет. 4 делится на 2, но не делится на10.

Учитель: Если число делится на 10, то оно делится на 5

Дети: Да верно. Потому, что на 10 делится число, которое заканчивается цифрой 0. Но и при делении на 5 оно может заканчиваться на цифру 0. Урок подходит к концу. Сегодня мы изучили признаки делимости на 2, на 5 и на 10.Давайте еще раз сформулируем и проговорим эти признаки.

Дети еще раз проговаривают изученные признаки делимости.

Учитель: Хорошо мы сегодня потрудились. Давайте запишем домашнее задание.

Дети записываю домашнее задание.

Учитель: Всем спасибо. Урок закончен.

Заключение

Из всего вышеизложенного становится понятно, для того чтобы в учащихся проявилась творческая активность в процессе обучения математике, эвристический метод является одним из основных методов обучения.

Столкнувшись с проблемой в процессе изучения математике, эта проблема становится своеобразным стимулом для изучения при эвристическом подходе. Если учащийся обнаруживает у себя не достаточный запас знаний для решения математической задачи, то он сам стремится заполнить этот пробел, самостоятельно делая открытие того или иного свойства, закономерности, тем самым обнаруживая полезность и увлекательность эвристического метода. Задача учителя сводится к тому, чтобы направить деятельность учащегося на решение проблемы, которая должна оказаться ему по силам.

Опыт многих учителей, широко применяющих эвристический метод, показал, что он влияет на отношение учащихся к учебной деятельности. Приобретя "вкус" к эвристике, учащиеся начинают расценивать работу по "готовым указаниям", как работу неинтересную и скучную. Наиболее значимыми моментами их учебной деятельности на уроке и в домашних условиях становятся самостоятельные "открытия" того или иного способа решения задачи. Явно возрастает интерес учащихся к тем видам работ, в которых находят применение эвристические методы и приемы. [7].

Эвристические уроки по математике очень ценны, они воспитывают учащихся, делают их самостоятельными, способствуют формированию собственной точки зрения, своего миропонимания. При решении творческих задач учащийся проходит все этапы творческого мышления.

На уроках математики 5-6 классов, для развития творческого мышления, можно применять следующие эвристические приемы:

- работа с гипотезами;

- моделирование проблемной ситуации;

- прием конкретизации проблемной ситуации;

- прием переструктурирования задачи;

- прием разбиения задачи на части.

Применение эвристических методов обучения требует, к сожалению, гораздо большего количества времени, чем изучение того же вопроса методом готового решения. По этой причине, применения эвристического метода на каждом уроке невозможно. К тому же применение только одного метода в обучении противопоказанно, даже если этот метод очень эффективный.

Однако следует отметить, что "время, затраченное на фундаментальные вопросы, проработанные с личным участием учащихся,- не потерянное время: новые знания приобретаются почти без затраты усилий благодаря ранее полученному глубокому мыслительному опыту". [14]

У эвристического метода обучения есть еще один недостаток - в большой степени применение этого метода зависит от уровня обученности и развития учащихся, особенно от сформированности их познавательных умений, а также опыта и образованности учителя.

Литература

1. Скафа Е., Власенко Е., Гончарова И. Комплексный подход к развитию творческой личности через систему эвристических заданий по математике: Книга для учителя [Текст]. - Донецк: ТЕАН, 2003.

2. Семенов Е.Е. Размышления об эвристиках //Математика в шк. – 1995. - № 5. – C. 39-43.

3. Хуторской А.В. «Эвристическое обучение», Москва, 2000.

4. Гурова Л.Л. Психологический анализ решения задач. – Воронеж: Изд – во Воронеж. ун – та, 1976.

5. Ильина Т.А. Педагогика. – М.: Просвещение, 1984.

6.Богословская Д.Б. Об эвристической функции модели проблемной ситуации //сб. «Проблемы эвристики». – М.: изд-во «Высшая школа»,1969.

7. Кулюткин Ю.К., «Эвристические методы в структуре решений», М.: Педагогика, 1970.

8. Коменский Я.А. Великая дидактика. – М.: Педагогика, 1989.

9. Выготский Л.С. Педагогическая психология / Под ред. В.В.Давыдова. - М.: Педагогика-Пресс, 1996.

10. Гальперин П.Я., Данилов, В.Л. Воспитание систематического мышления в процессе решения малых творческих задач. // Вопросы психологии. – 1980. - №1.

11. Андреев В.И. Диалектика воспитания и самовоспитания творческой личности. Основы педагогики творчества. – Казань: 1988.

12. Андреев В.И. Диалектика воспитания и самовоспитания творческой личности. Основы педагогики творчества. – Казань: 1988.

13. Лернер И.Я. Дидактические основы методов обучения. – М.: Педагогика, 1981.

14. Окунев А.А. Как учить не уча. – Спб.: Питер-пресс, 1996.

15. Кулюткин Ю.Н., Сухобская, Г.С. Развитие творческого мышления школьников. – Л.: 1967.

16. Воробьёв Г.Г. Школа будущего начинается сегодня. – М., 199117. Сойер, У.У. Прелюдия к математике. – М.: Просвещение, 1972.

18. Фридман Л.М. Теоретические основы методики обучения математики. – М.: Флинта, 1998.

19. Ильясов И.И. Система эвристических приемов решения задач. – М.: РОУ, 1992.

20. Пойа Д. Как решать задачу. // Квантор. – 1991. - № 1.

21. Пойа Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание. – М.: Наука, 1970.

33