Содержание
Содержание
|
| Стр. |
| Введение | 3 |
| Многовариантные задачи | 4 |
Взаимное расположение линейных фигур | 6 |
Взаимное расположение различных точек на прямой | 6 |
Взаимное расположение точки и отрезка, лежащих на одной прямой. | 7 |
Взаимное расположение прямой и точки вне прямой | 8 |
Взаимное расположение точки и двух параллельных прямых | 11 |
Взаимное расположение окружностей | 13 |
Расположение центров окружностей относительно общей касательной | 13 |
Расположение центров окружностей относительно их общей точки касания. | 14 |
Расположение центров окружностей относительно общей хорды | 16 |
Взаимное расположение элементов фигур | 16 |
Вы бор расположения вершин многоугольника | 16 |
Выбор углового элемента | 20 |
Соответствие между множеством фигур и множеством их свойств | 22 |
Неопределенность между значениями синуса (косинуса) угла и видом угла
| 22 |
| Заключение | 24 |
| Список литературы | 25 |
| Приложение | 26 |
Введение.
В 7 – 9 классах на уроках геометрии я изучал свойства отрезков, углов, треугольников, четырехугольников, окружностей, для меня стали привычными понятиями определения, теоремы, доказательства. При изучении курса геометрии решению задач уделяется большое внимание. Все новые понятия, теоремы, свойства геометрических фигур, способы рассуждений рассматриваются в процессе решения задач. Поэтому моя работа состоит из решения задач.
В работе мной рассмотренны различные многовариантные задачи, которые были предложены на ЕГЭ.
Цель работы
Систематизировать многовариантные планиметрические задачи, выделить дополнительные свойства геометрических фигур и их элементов, изучить приемы решения этих задач.
проиллюстрировать широкие возможности использования хорошо усвоенных школьных знаний,
подготовиться к сдаче ЕГЭ.
Актуальность работы
Анализ результатов математической подготовки учащихся, проявляющихся на ЕГЭ, позволяет сделать вывод о недостаточном уровне освоения некоторых значимых умений, например таких как: анализировать условие задачи. В работе я рассматриваю некоторые виды планиметрических задач, и при знании приведенных приемов решения, многие из них вполне посильны для любого школьника. Актуальность работы в том, что задачи такого типа входят в Единый Государственный Экзамен по математике, кроме того они развивают первоначальные навыки исследовательской деятельности и в перспективе возможности успешного овладения курса математики в высших учебных заведениях.
Объект исследования
Планиметрические задачи с неоднозначным решением.
Предмет исследования
Анализ условия задач. Систематизация задач.
Методы исследования
Самостоятельное решение задач, использование литературы разного типа, систематизация задач.
Многовариантные задачи
В отличии от большинства задач школьного учебника рассмотренные мной задачи содержат некоторую неопределенность, которая позволяет трактовать условие неоднозначно. В результате не удается построить чертеж по условию задачи в одном варианте. Поэтому подобные задачи называют многовариантными. Перебор вариантов является частью решения задач такого типа.
Можно выделить следующие причины, ведущие к неоднозначной трактовке условия задачи.
точки и прямой (расположение точки на прямой или в одной из полуплоскостей);
точки и двух параллельных прямых;
точки и отрезка, лежащих на одной прямой (или трех точек, лежащих на одной прямой);
точки и окружности (внутри, на или вне окружности);
точки и многоугольника (внутри, на сторонах или вне многоугольника;
вписанный угол, опирающийся на хорду (вид угла – острый, прямой или тупой);
треугольник, вписанный в окружность (расположение центра окружности относительно треугольника);
трапеция, вписанная в окружность (расположение центра окружности относительно трапеции).
имеется произвол в выборе углового элемента;
имеется произвол в выборе отношения отрезков, площадей фигур.
В задаче рассматриваются объекты, которым приписываются определенные свойства, но неуказан порядок соответствия между множеством объектов и множеством их свойств. Например,
условие задачи не привязано к конкретной вершине многоугольника;
в равнобедренном треугольнике, но не указаны равные стороны;
при разбиении отрезка на заданные части или в данном отношении не указано относительно, какого из концов;
при заданном отношении пары сторон многоугольника не указано, какой конкретно;
при разбиении отрезка на заданные части или в данном отношении не указано относительно, какого из концов;
при пересечении прямых задано значение одной из двух пар вертикальных углов, но не указано какой конкретно;
не указан тип касания (внешний или внутренний),
расположение центров окружностей относительно их общей хорды
Взаимное расположение линейных фигур
Геометрической фигурой называют любую совокупность точек, линий, поверхностей. Линейной будем считать фигуру, представляющую собой точку, отрезок, луч, прямую. При решении задач условие может трактоваться неоднозначно, если для рассматриваемых фигур не указано их взаимное расположение.
Взаимное расположение различных точек на прямой.
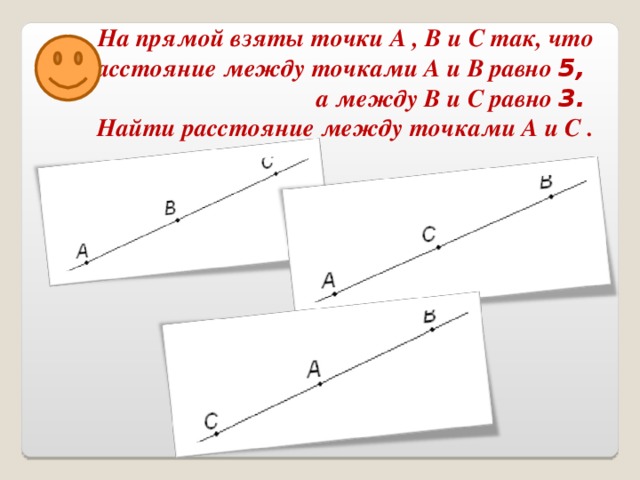
Задача 1. На прямой взяты точки A ,B и C так, что расстояние между
точками A и B равно 5, а между B и C равно 3. Найдите расстояние между
точками A и C .
Исследуя условие задачи, замечу, что не указано взаимное расположение точек A , B и C на прямой относительно друг друга. Можно записать шесть различных вариантов расположение этих точек.
Дано: АВ = 5, ВС = 3.
Найти: АС.
Решение.
A, B, C или C, B, A(точка В лежит между точками А и С);
А, С, В, или B, C, A(точка С лежит между точками А и В;
C, A, B или B, A, C(точка А лежит между точками В и С).
Вариант № 1. Если точка B лежит между A и C , то AC = AB+ BC = 5+ 3 = 8 или CA = CB + BA = 3 + 5 = 8 , т.е. расстояние между точками A и C 
равно 8.
Вариант № 2. Если точка C лежит между A и B, то AB = AC+ CB и тогда AC = 5 3 = 2 или BA = BC + CA и тогда CA = 5 3 = 2 , т.е. расстояние между точками A и C равно 2.
Вариант № 3. Случай, когда точка A лежит между C и B невозможен, так как тогда по условию CB AB .
Ответ: 8 или 2.
Взаимное расположение точки и отрезка, лежащих на одной прямой.
Задача №2. В прямоугольнике ABCD AB = 2, BC =  , Точка Е на прямой АВ выбрана так, что
, Точка Е на прямой АВ выбрана так, что AED =
AED = DEC. Найдите АЕ.
DEC. Найдите АЕ.
Исследуя условие задачи, выясняю, что точка Е может лежать как на стороне АВ, так и на ее продолжении слева и справа от отрезка.
Дано: ABCD – прямоугольник,  AED =
AED = DEC, E
DEC, E AB
AB
Найти: AE.
Решение:
Вариант № 1. Точка E лежит на стороне AB.
1). Рассмотрим AB DC и секущую DE:
DC и секущую DE: 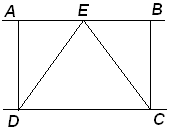
 DEC =
DEC =  AED =
AED =  ADE =
ADE =  EDC =
EDC =
 DEC – равнобедренный = EC = CD = 2.
DEC – равнобедренный = EC = CD = 2.
2). Рассмотрим  BEC: BC =
BEC: BC =  , EC = 2 = = EC2 = BC2 + BE2 = BE2 = EC2
, EC = 2 = = EC2 = BC2 + BE2 = BE2 = EC2 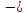 BC2 = 22
BC2 = 22  2 =
2 =
= 4 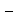 3 = 1.
3 = 1.
3). Т.к. BE2 = 1 = BE = 1 = AE = AB 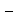 BE = 2
BE = 2  1 = 1.
1 = 1.
Вариант № 2. Точка E лежит за точкой B.
1). Рассмотрим AB DC и секущую DE:
DC и секущую DE:  DEC =
DEC =  AED =
AED = EDC =
EDC =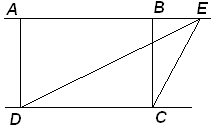
 DEC – равнобедренный =
DEC – равнобедренный =
EC = CD = AB = 2.
2). Рассмотрим  BEC: BC =
BEC: BC =  , EC = 2 =
, EC = 2 =
BE2 = EC2  BC2 = 22
BC2 = 22  2 = 4
2 = 4  3 = 1, = BE = 1.
3 = 1, = BE = 1.
3). Т.к. E лежит за точкой B = AE = AB + BE = 2 + 1 = 3.
Вариант № 3. Точка E лежит перед точкой A.
 AED
AED  DEC но нам дано, что
DEC но нам дано, что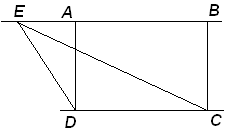
 AED =
AED = DEC = такой
DEC = такой
вариант существовать не может.
Ответ: 1 или 3.
Взаимное расположение прямой и точки вне прямой
Задача 3. Дан параллелограмм ABCD. Биссектрисы его углов А и D делят сторону BC на три равные части. Вычислите стороны параллелограмма, если его периметр равен 40.
Исследуя условие задачи, замечу, что биссектрисы углов А и D могут пересекаться внутри параллелограмма или вне его.
Дано: ABCD - параллелограмм, А N и DK – биссектрисы,
ВN = NК = КС, РАВСD = 40.
Найти: АВ, ВС, CD, DA.
Решение.
Обозначим точку пересечения биссектрис через М, а точки пересечения биссектрис АМ и DM со стороной BC через N и K соответственно. В зависимости от расположения точки М относительно прямой (отрезка) CD возможны два варианта для чертежа.
Вариант № 1.
Пусть точка M расположена вне параллелограмма. Так как биссектриса АМ отсекает от параллелограмма равнобедренный треугольник ABN, то AB = BN = NK = KC = x .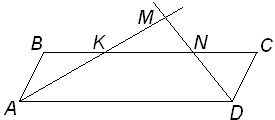
Периметр параллелограмма равен 40, поэтому из уравнения 2(x +3x) = 40
находим x = 5 . Значит, AB = 5 , BC = 15.
Вариант № 2.
Если точка M расположена внутри параллелограмма, то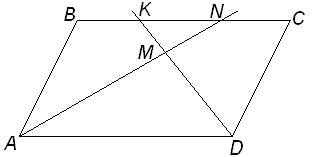
NC = x и AB = BN = 2x
Из уравнения 2(2x + 3x) = 40 находим x = 4 .
Значит, AB = 8 и BC = 8 = 4 = 12 .
Ответ: 5; 15 или 8; 12.
Задача № 4. Дан параллелограмм ABCD, АВ = 2, ВС =3, 𝘓А = 60°. Окружность с центром в точке О касается биссектрисы угла D и двух сторон параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь четырехугольника ABOD.
Исследуя условие задачи, получаю, что окружность может находиться по разные стороны от биссектрисы угла D.
Дано: ABCD – параллелограмм, AB = 2, BC = 3,  A= 60
A= 60 , окружность с центром O касается биссектрисы
, окружность с центром O касается биссектрисы  D и двух сторон параллелограмма, исходящих из вершины одного его острого угла.
D и двух сторон параллелограмма, исходящих из вершины одного его острого угла.
Найти: S ABOD.
Решение:
Вариант №1. Окружность вписана в угол с вершиной С.
1). Рассмотрим ABCD – параллелограмм: AB = CD, BC = AD,  A =
A =  C = 60
C = 60 =
=  D = 180
D = 180
 A = 180
A = 180 60
60 = 120
= 120 =
=  B,
B,  C =
C =  CDM = 60
CDM = 60 =
=  CMD = 180
CMD = 180
 60
60 60
60 = 60
= 60 =
=  MDC – равносторонний = CM = CD = DM = 2.
MDC – равносторонний = CM = CD = DM = 2.
2). r = R · cos  , где r – радиус вписанной окружности, R – радиус описанной окружности, а n – кол-во углов; an = R
, где r – радиус вписанной окружности, R – радиус описанной окружности, а n – кол-во углов; an = R , где an – длина сторон = 2 = R
, где an – длина сторон = 2 = R = R =
= R =  ; r =
; r =  · cos
· cos  =
=  =
= .
.
3). SCOD =  · CD · r =
· CD · r =  ; SBOC =
; SBOC = · BC · r =
· BC · r =  .
.
4). S ABOD = 2 · 3  =
=  .
.
Вариант №2. Окружность вписана в угол с вершиной А.
1). Рассмотрим ABCD – параллелограмм: AB = CD, BC = AD,
 D =
D =  B,
B,  A =
A = C = 60
C = 60 =
=  D = 180
D = 180
 A = 180
A = 180 60
60 = 120
= 120 =
=  B,
B,
 A =
A =  ADM = 60
ADM = 60 =
=  AMD = 180
AMD = 180 60
60 60
60 = 60
= 60 =
=
 AMD – равносторонний = AM = AD = DM = 3.
AMD – равносторонний = AM = AD = DM = 3.
2). r = R · cos , где r – радиус вписанной окружности, R – радиус описанной окружности, а n – кол-во углов; an= R
, где r – радиус вписанной окружности, R – радиус описанной окружности, а n – кол-во углов; an= R , где an – длина сторон =
, где an – длина сторон =
3 = R  = R =
= R = r =
r = · cos
· cos =
= =
= .
.
3). SAOD = · AD · r =
· AD · r = ; SAOB =
; SAOB =  · AB · r =
· AB · r =  .
.
4). S ABOD = SAOD + SAOB =  +
+  =
=  .
.
Ответ:  или
или  .
.
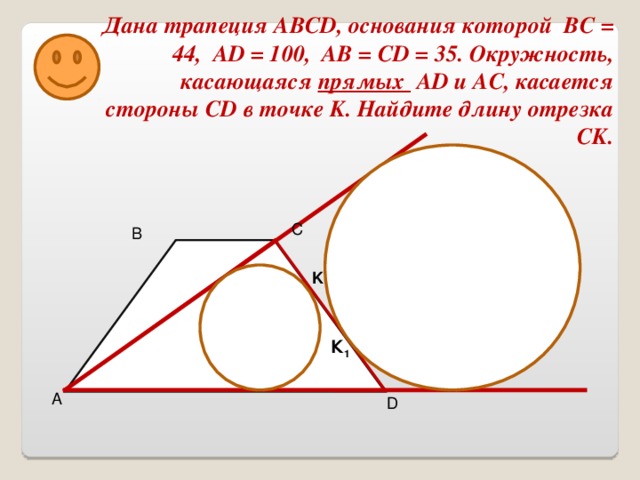
Задача № 5. Дана трапеция ABCD, основания которой ВС = 44, AD = 100, AB = CD = 35. Окружность, касающаяся прямых AD и AC, касается стороны CD в точке K. Найдите длину отрезка CK.
Исследование условия приводит к выводу, что окружность касается прямых AD и АС и стороны СК, таким образом, она может лежать внутри трапеции и вне ее.
Дано: ABCD –трапеция, BC = 44, AD = 100, AB = CD = 35, AD, AC и CD касательные , K CD.
CD.
Найти: CK.
Решение:
Вариант №1. Окружность вписана в треугольник ACD.
1). AH = LD, BC = HL =
LD =  (AD
(AD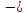 BC) = 28.
BC) = 28.
2). Рассмотрим  CLD: CD = 35,
CLD: CD = 35,
LD = 28 = CD2 = LD2 + CL2 =
CL = 21.
3). Рассмотрим  ACL: CL = 21,
ACL: CL = 21,
AL = BC + AH = 72 = AC2 = AL2 + CL2 = AC = 75.
4). Отрезки касательных к окружности, проведённые из одной точки, равны
= AM = AN, CM = CK, DN = DK = CK =  =
=  = 5.
= 5.
Вариант №2. Окружность лежит вне трапеции.
1). AH = LD, BC = HL =
LD =  (AD
(AD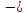 BC) = 28.
BC) = 28.
2). Рассмотрим  CLD: CD = 35,
CLD: CD = 35,
LD = 28 = CD2 = LD2 + CL2 =
CL = 21.
3). Рассмотрим  ACL: CL = 21, AL = BC + AH = 72 = AC2 = AL2 + CL2 = AC = 75.
ACL: CL = 21, AL = BC + AH = 72 = AC2 = AL2 + CL2 = AC = 75.
4). Отрезки касательных к окружности, проведённые из одной точки, равны: AM = AN, CM = CK, DN = DK =
AM =  =
= = CK = AM
= CK = AM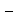 AC = 105
AC = 105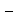 75 = 30.
75 = 30.
Ответ: 5 или 30.
Взаимное расположение точки и двух параллельных прямых
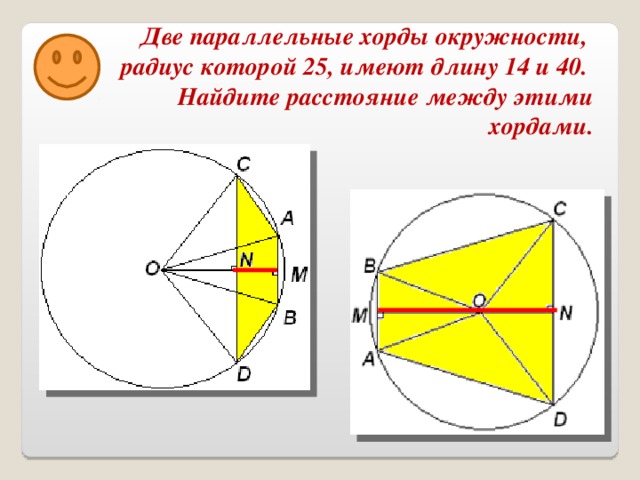
Задача № 6. Две параллельные хорды окружности, радиус которой 25, имеют длину 14 и 40. Найдите расстояние между этими хордами.
Исследование: хорды могут лежать относительно центра окружности по одну сторону и по разные стороны.
Дано: AB и CD – две параллельные хорды окружности,
R = 25, AB=14, CD=40.
Найти: MN – расстояние между хордами.
Решение:
Вариант №1. Хорды расположены по разные стороны от центра окружности.
1).Рассмотрим  BOA: OB = OA = OM – медиана и высота = BM = MA =
BOA: OB = OA = OM – медиана и высота = BM = MA =  BA = 7.
BA = 7.
2). Рассмотрим  MOA: OA = 25, MA = 7 = 252 = 72 + OM2 = OM = 24.
MOA: OA = 25, MA = 7 = 252 = 72 + OM2 = OM = 24.
3). Рассмотрим  DOC: OC = OD = ON – медиана и высота = DN = NC =
DOC: OC = OD = ON – медиана и высота = DN = NC =  DC = 20.
DC = 20.
4). Рассмотрим  CON: OC = 25, NC = 20 = 252 = 202 + ON2 = ON = 15 = = MN = 24 + 15 = 39.
CON: OC = 25, NC = 20 = 252 = 202 + ON2 = ON = 15 = = MN = 24 + 15 = 39.
Вариант №2. Хорды расположены по одну сторону от центра окружности.
1). Рассмотрим  BOA: OB = OA = OM - медиана и высота = BM = MA =
BOA: OB = OA = OM - медиана и высота = BM = MA =  BA = 7.
BA = 7.
2). Рассмотрим  MOA: OA=25, MA = 7 = 252 = 72 + OM2 = OM = 24.
MOA: OA=25, MA = 7 = 252 = 72 + OM2 = OM = 24.
3). Рассмотрим  DOC: OC = OD = ON
DOC: OC = OD = ON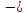 медиана и высота =
медиана и высота =
DN = NC =  DC = =20.
DC = =20.
4). Рассмотрим  CON: OC = 25, NC = 20 = 252 = 202 + ON2 = ON = 15 = = MN = 24
CON: OC = 25, NC = 20 = 252 = 202 + ON2 = ON = 15 = = MN = 24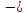 15 = 9.
15 = 9.
Ответ: MN = 39 или MN = 9.
Задача № 7. Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.
Задача решается аналогично задаче 6.
Взаимное расположение окружностей
Взаимное расположение окружностей можно различать по внешнему признаку (касающиеся, пересекающиеся, непересекающиеся) или по внутреннему признаку (взаимное расположение центров окружностей относительно общей касательной, общей хорды и т.д.).
Расположение центров окружностей относительно общей касательной
В условии задачи этого типа фигурируют две окружности, касающиеся одной прямой, но не указано расположение центров этих окружностей относительно этой прямой. Соответственно эта прямая является внутренней или внешней касательной для этих окружностей.
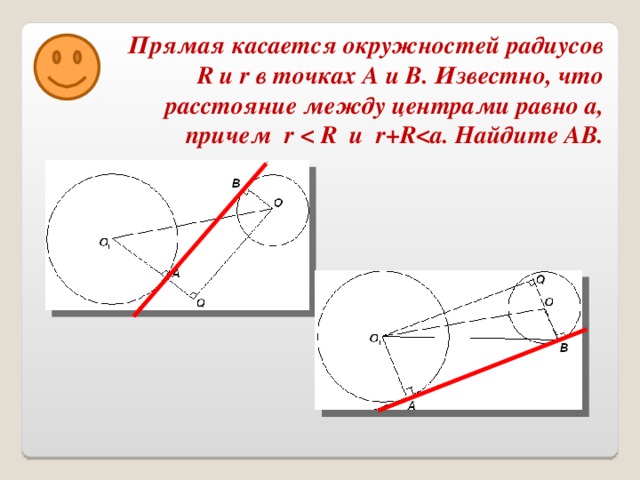
Задача № 8. Прямая касается окружностей радиусов R и r в точках А и В. Известно, что расстояние между центрами равно a, причем r R и r+Ra. Найдите АВ.
Исследование: окружности могут лежать по разные стороны от касательной и по одну сторону.
Дано: Прямая касается окружностей, с радиусом R и r, в точках A и B, расстояние между центрами окружностей равно a, r R, r + R a.
Найти: AB.
Решение.
Вариант №1. Внутренняя касательная.
1). Достроим отрезок AQ и QO: AQ O1A, AQ = BO, AQ
O1A, AQ = BO, AQ  O1A; QO = AB =
O1A; QO = AB =
ABOQ – прямоугольник.
2). Рассмотрим  O1OQ: OO1 – гипотенуза = OO1 = (R + r)2 + AB2 = AB =
O1OQ: OO1 – гипотенуза = OO1 = (R + r)2 + AB2 = AB =  .
.
Вариант №2. Внешняя касательная.
1). Достроим BQ и O1Q: AO1 BQ,
BQ,
AO1 = BQ, O1Q=AB, O1Q AB,
AB,
OQ = AO1 – OB = R– r.
2). Рассмотрим  O1QO: OO1 = a, O1Q = AB, OQ = AO1– OB = OO1 = OQ2 + O1Q2 = O1Q =
O1QO: OO1 = a, O1Q = AB, OQ = AO1– OB = OO1 = OQ2 + O1Q2 = O1Q =  =
=
O1Q =  , O1Q = AB = AB =
, O1Q = AB = AB =  .
.
Ответ:  или
или  .
.
Расположение центров окружностей относительно их общей точки касания.
В условии задачи этого типа фигурируют две окружности, но не указан тип касания (внешний или внутренний).
Задача № 9. Вершина равнобедренного треугольника с боковой стороной 5 и основанием 8 служит центром данной окружности радиуса 2. Найдите радиус окружности, касающейся данной и проходящей через концы основания треугольника.
Решение.
Пусть D – середина основания AC данного треугольника ABC .
Обозначим через E и F точки пересечения прямой BD и окружности радиуса 2 с центром в точке B . Тогда : AD = 4 , BD = 3 , ED = 1, FD = 5 .
Из теоремы Пифагора для прямоугольных треугольников AED и AFD
соответственно имеем:
AE = =
=  ,
,
AF =  =
=  .
.
Находим площади треугольников AEC и AFC :
S AEC =  AC · ED =
AC · ED =  · 8 · 1 = 4
· 8 · 1 = 4
S AEC =  AC · FD =
AC · FD =  · 8 · 5 = 20.
· 8 · 5 = 20.
Возможны два случая расположения указанной в условии окружности в
зависимости от типа касания с данной окружностью. В обоих случаях центры O1 и O2 этих окружностей будут лежать на биссектрисе угла прямой BD.
Вариант № 1. Пусть окружности касаются внешним образом.
Тогда искомая окружность описана около треугольника AEC . Найдем ее радиус по формуле R =  =
=  =
=  .
.
Вариант №2. Пусть окружности касаются внутренним образом. Тогда искомая окружность описана вокруг треугольника AFC .
Найдем ее радиус R =  =
=  =
=  .
.
Ответ:  или
или  .
.
Расположение центров окружностей относительно общей хорды
В условии задачи этого типа рассматриваются две пересекающиеся окружности, но не указано расположение центров окружностей относительно их общей хорды.
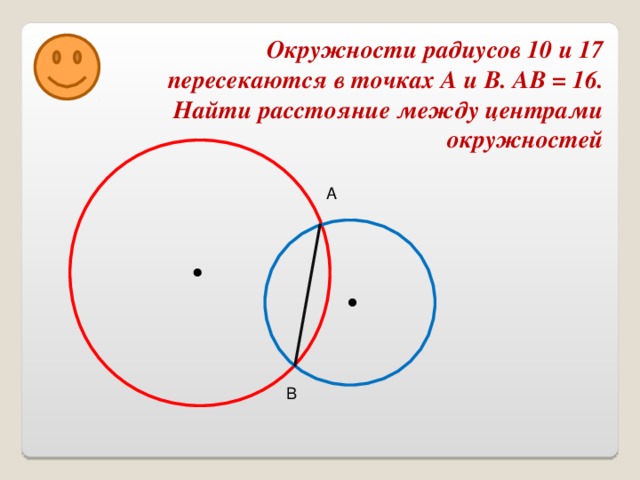
Задача №12. Окружности радиусов 10 и 17 пересекаются в точках А и В. Найдите расстояние между центрами окружностей, если АВ = 16.
Дано: Окружности радиусов 10 и 17 пересекаются в точках A и B, AB=16.
Найти: OQ.
Решение:
Вариант №1. Центры окружностей лежат по разные стороны от их общей хорды АВ.
1).  QKB =
QKB = OKA = 90
OKA = 90 , BK = KA = 8,
, BK = KA = 8,
OQ = QK + KO.
2). Рассмотрим  QKB: BK = 8, QB = 17 =
QKB: BK = 8, QB = 17 =
172 = QK2 + 82 = QK = 15.
3). Рассмотрим  BKO: BK = 8, OB = 10 = 102 = QK2 + 82 = OK = 6 =
BKO: BK = 8, OB = 10 = 102 = QK2 + 82 = OK = 6 =
OQ =15+6 = 21.
Вариант №2. Центры окружностей лежат по одну сторону от общей хорды АВ.
1).  QKB =
QKB = OKA =9 0
OKA =9 0 , BK = KA = 8,
, BK = KA = 8,
OQ = QK – KO.
2). Рассмотрим  QKB: BK = 8, QB = 17 =
QKB: BK = 8, QB = 17 =
172 = QK2 + 82 = QK = 15.
3). Рассмотрим  BKO: BK = 8, OB = 10 =
BKO: BK = 8, OB = 10 =
102 = QK2 + 82 = OK = 6 =
OQ = 15 – 6 = 9.
Ответ: 21 или 9.
Взаимное расположение элементов фигуры.
В задачах этого типа фигурируют однотипные элементы фигуры (вершины, стороны, дуги, углы, высоты, биссектрисы, многоугольники и т.д.), однако условие допускает произвол выбора конкретного элемента из имеющихся у рассматриваемой фигуры.
Выбор обозначений вершин многоугольника.
К задачам этого типа относят такие задачи, условие которых допускает различные решения в зависимости от варианта буквенного обозначения вершин многоугольника.
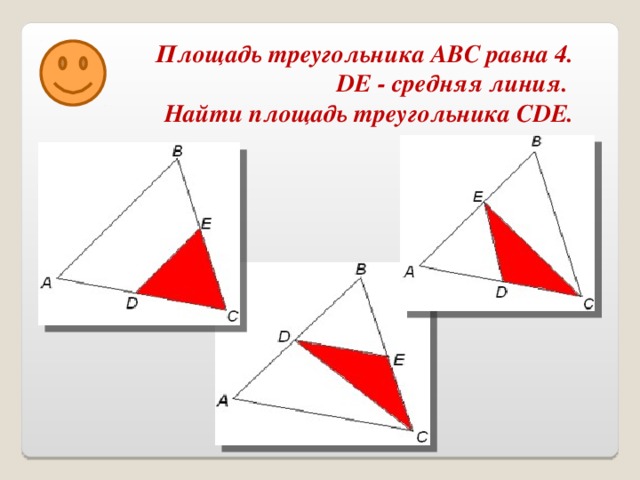
Задача №13. Площадь треугольника ABC равна 4. DE - средняя линия. Найдите площадь треугольника CDE.
При решении данной задачи неоднозначность состоит в выборе средней линии. Рассмотрим три случая.
Дано:  ABC, S
ABC, S ABC = 4, DE – средняя линия.
ABC = 4, DE – средняя линия.
Найти: S CDE.
CDE.
Вариант №1. Отрезок DE параллелен отрезку АВ.
 CDE подобен
CDE подобен  ABC =
ABC =  = K =
= K =  =
=
S CDE = S
CDE = S ABC
ABC K2 = 4
K2 = 4  2 = 1
2 = 1
Вариант №2. Отрезок DE параллелен отрезку ВС.
1). Отрезок DE параллелен отрезку ВС. Так как CE – медиана треугольника АBC, то
S AEC
AEC  S
S ABC = 2
ABC = 2
2). DE 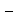 медиана
медиана  AEC =
AEC =
S CDE =
CDE =  S
S AEC = 1
AEC = 1
Вариант №3. Отрезок DE параллелен отрезку АС.
1). Отрезок DE параллелен отрезку AC. Так как CD – медиана треугольника АBC, то S CDB=
CDB=  S
S ABC = 2
ABC = 2
2). DE 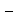 медиана
медиана  CDB = S
CDB = S CDE =
CDE = S
S CDB = 1.
CDB = 1.
Ответ: S CDE = 1.
CDE = 1.
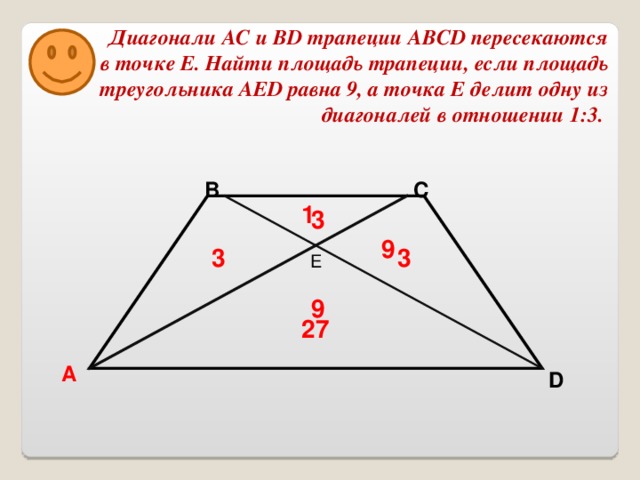
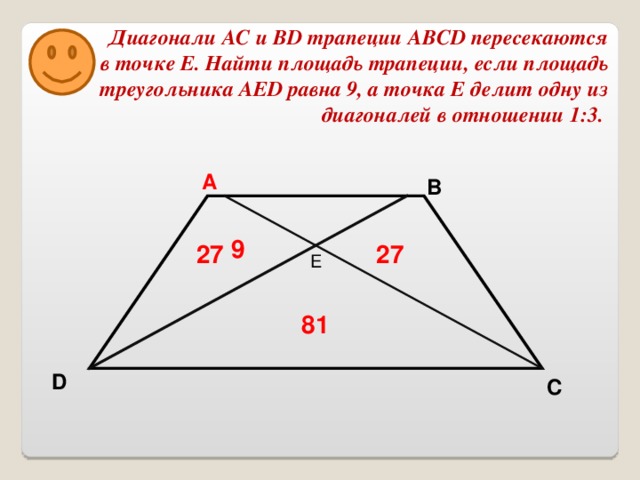
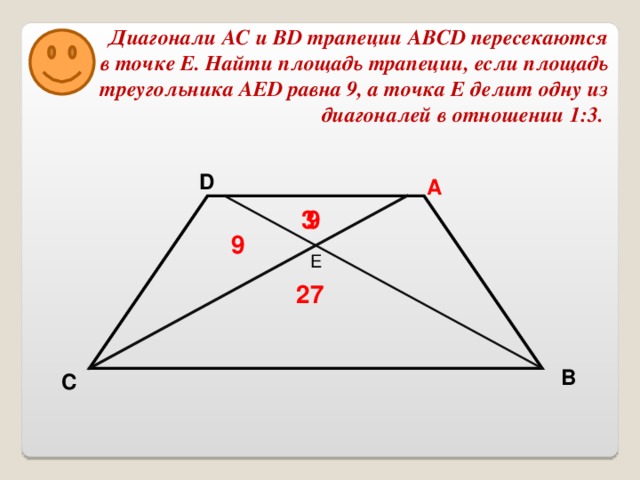
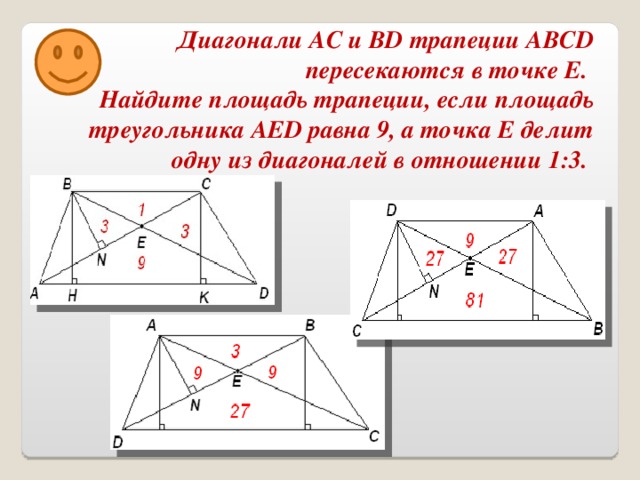
Задача №14. Диагонали АС и BD трапеции ABCD пересекаются в точке Е. Найдите площадь трапеции, если площадь треугольника AED равна 9, а точка Е делит одну из диагоналей в отношении 1:3.
Исследование задачи показывает, что неоднозначность в условии, состоит в выборе варианта буквенного обозначения вершин трапеции и дополнительно к этому в выборе большего основания.
Дано: ABCD – трапеция, S AED = 9, точка E пересекает одну из диагоналей в отношении
AED = 9, точка E пересекает одну из диагоналей в отношении  .
.
Найти: S ABCD.
Пусть точка Е делит диагональ в отношении 1:3, считая от вершины верхнего основания.
Вариант №1.  Основания AD и ВC.
Основания AD и ВC.
1).  BEC подобен
BEC подобен  AED по 3 углам =
AED по 3 углам =  =
=  = K =
= K =  = K2 = = (
= K2 = = ( ) 2 =
) 2 = 
= S BEC = 1
BEC = 1
2). Рассмотрим  ABD и
ABD и  ACD:
ACD:
AD – общая, BH = CK – высоты = S ABD = S
ABD = S ACD = S
ACD = S ABE = S
ABE = S CED.
CED.
3). Рассмотрим  BEC и
BEC и  ABE: BN – общая высота,
ABE: BN – общая высота,  =
=  =
=
S ABE = 3S
ABE = 3S BCE = 3 = т.к. S
BCE = 3 = т.к. S ABE = S
ABE = S CED = 3 =
CED = 3 =
S ABCD = 1+3+3+9 = 16.
Вариант №2. Основания AВ и DC.
1). Т.к.  =
=  = S
= S AED = = 3S
AED = = 3S AEB = S
AEB = S AEB = 3.
AEB = 3.
2).  DEC подобен
DEC подобен  AEB по 3 углам ,
AEB по 3 углам ,
т.к.  =
=  = K =
= K =  = K2 = (
= K2 = ( ) 2 =
) 2 =  = S
= S DEC = 27.
DEC = 27.
3). Рассмотрим  DAC и
DAC и  DBC: высота – общая, DC – общая =
DBC: высота – общая, DC – общая =
S DAC = S
DAC = S DBC = S
DBC = S DAE = S
DAE = S BEC = 9 = S ABCD =3+9+9+27 = 48.
BEC = 9 = S ABCD =3+9+9+27 = 48.
Вариант №3. Основания AD и ВC.
1). Т.к.  =
=  = S
= S DEC = = 3S
DEC = = 3S DEA = S
DEA = S DEC = 27 .
DEC = 27 .
2).  DEA подобен
DEA подобен  CEB по 3 углам = т.к.
CEB по 3 углам = т.к.  =
=  = K =
= K =
 = K2 = (
= K2 = ( ) 2 =
) 2 =  = S
= S CEB = 81.
CEB = 81.
3). Рассмотрим  CDB и
CDB и  CAB: высота – общая, CB – общая =
CAB: высота – общая, CB – общая =
S CDB = S
CDB = S CAB = S
CAB = S DEC = S
DEC = S AEB = 27 =
AEB = 27 =
S ABCD = 9+27+27+81 = 144.
Вариант №4. Основания AВ и DC.
(Решение аналогично варианту 2)
Замечание. В задаче кроме неопределенности в выборе оснований трапеции имеется неопределенность в выборе отношения. Я рассмотрел этот случаи, когда точка Е делит диагональ в отношении 1: 3, считая от вершины нижнего основания. Решения аналогичны рассмотренным, только рисунок выглядит перевернутым (нижнее основание меньше верхнего).
Ответ: 16; 48; 144.
Выбор углового элемента.
Задача №15. Площадь треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами.
Исследование: угол треугольника может быть острый, прямой или тупой.
Дано: S ABC=12, АВ = 8 и ВС = 6.
ABC=12, АВ = 8 и ВС = 6.
Найти: Угол АВС .
Решение:
Вариант №1. Угол АВС прямой.
Предположим, что  АВС = 90
АВС = 90 = S
= S ABC =
ABC =  BC· AC =
BC· AC =  8· 6 = 24, но нам дано, что S
8· 6 = 24, но нам дано, что S ABC = 12 =
ABC = 12 =  АВС ≠ 90
АВС ≠ 90 .
.
Вариант №2. Угол АВС острый.
1). S =
=  · h · AВ = 12 =
· h · AВ = 12 =  · h· 8 = h = 3 = BH.
· h· 8 = h = 3 = BH.
2). Рассмотрим  BHC:
BHC:  H = 90
H = 90 , BH = 3, BC = 6 =
, BH = 3, BC = 6 =  C =
C =  ABC = 30
ABC = 30 , т.к. катет (BH) равен половине гипотенузы (BC).
, т.к. катет (BH) равен половине гипотенузы (BC).
Вариант №3. Угол АВС тупой.
1). S =
=  · h · AB = 12=
· h · AB = 12=  · h · 8 = h = 3 = CH.
· h · 8 = h = 3 = CH.
2). Рассмотрим  HBC:
HBC:  H = 90
H = 90 , CH = 3, BC = 6 =
, CH = 3, BC = 6 =  B = 30
B = 30 =
=  ABC = 180
ABC = 180 30
30 = 150
= 150 .
.
Ответ: 30 или 150
или 150 .
.
Задача № 16. В параллелограмме ABCD известны стороны AB = a,
BC = b и  A=α . Найдите расстояние между центрами окружностей, описанных около треугольников BCD и DAB.
A=α . Найдите расстояние между центрами окружностей, описанных около треугольников BCD и DAB.
Задача имеет разные решения в зависимости от того острый или тупой угол А.
Дано: ABCD – параллелограмм, AB = a, BC = b,  A=α
A=α
Найти: Расстояние между центрами окружности, описанных около треугольников BCD и DAB.
Решение:
Вариант №1.  α .
α .
1). Рассмотрим  ABD и
ABD и  BDC: AD = BC; AB = DC; BD – общая
BDC: AD = BC; AB = DC; BD – общая
=  ABD =
ABD =  BDC.
BDC.
2).  BOD – центральный;
BOD – центральный;  BOD = 2α =
BOD = 2α =  BOK = α.
BOK = α.
3). Рассмотрим  BOK:
BOK:  K =
K =  ; ctg α =
; ctg α =  = OM = BK· ctg α.
= OM = BK· ctg α.
4). a2 = b2 + c2 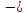 2· b · c · cos α; BD2 =AB2 +AD2 ̶ 2 · AB · AD · cos α = BD = .
2· b · c · cos α; BD2 =AB2 +AD2 ̶ 2 · AB · AD · cos α = BD = .
5). OQ = 2OK = 2 BK · ctg α = BD · ctg α.
Вариант №2  α
α  .
.
1).  BOD – центральный;
BOD – центральный;
 BOD = 360
BOD = 360 2α;
2α;
 BOD = 180
BOD = 180 α.
α.
2). Рассмотрим  BOM:
BOM:
 M = 90
M = 90 ; ctg α =
; ctg α =  =
=
OM = BM · ctg α; ctg BOD = ctg (180 α) =
α) =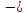 ctg α.
ctg α.
3). a2 = b2 + c2 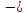 2 · b · c · cos α; BD2 = AB2 + AD2
2 · b · c · cos α; BD2 = AB2 + AD2 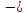 2 · AB · AD · cos α = = BD = .
2 · AB · AD · cos α = = BD = .
4). OQ = 2 OM = 2 BM· (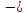 ctgα) =
ctgα) = 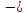 BD · ctgα.
BD · ctgα.
Ответ: BD · ctg α или 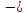 BD · ctg α.
BD · ctg α.
Соответствие между множеством фигур и множеством их свойств.
В задачах этого типа рассматриваются объекты, которым приписываются определенные свойства, но не указан порядок соответствия между множеством объектов и множеством их свойств.
Неопределенность между значением синуса (косинуса) угла и видом угла.
Задача 17. Средняя линия трапеции, вписанной в окружность с центром О, равна 3, синус угла АОВ равен  . Найдите высоту трапеции.
. Найдите высоту трапеции.
Исследование: sin  АОВ =
АОВ =  , следовательно, угол АОВ может быть и острым и тупым.
, следовательно, угол АОВ может быть и острым и тупым.
Дано: ABCD – трапеция, вписанная в окружность с центром O, MN – средняя линия, MN = 3, sinα = sin AOB =
AOB =  .
.
Найти: высоту трапеции.
Решение:
Вариант №1  AOB – острый
AOB – острый
1).  ADB и
ADB и  AOB опираются на одну дугу =
AOB опираются на одну дугу = ADB =
ADB = 
 AOB =
AOB =  =
=  .
.
2). Т.к. ABCD – равнобедренный =
= ABH =
ABH =  DCK = MX = YN,
DCK = MX = YN,
AH = KD т.к. MX и YN средние линии = 2MX = AH, 2YN = KD = YN + MX = KD = YN + MX + XY = HK + KD = 3.
3). tg  =
=  = BH = HD · tg
= BH = HD · tg  = 3tg
= 3tg  .
.
4). tg  =
=  ; cos
; cos =
=  =
=  = BH = 3 ·
= BH = 3 ·  : (1+
: (1+  ) = 1.
) = 1.
Вариант №2  AOB=90
AOB=90
Sin90 =1, но нам дано, что sin
=1, но нам дано, что sin AOB=
AOB=  = вариант не имеет решений.
= вариант не имеет решений.
Вариант №3  AOB90
AOB90
1).  ADB и
ADB и  AOB опираются на одну дугу =
AOB опираются на одну дугу =  ADB =
ADB = 
 AOB =
AOB =  =
=  .
.
2). Т.к. ABCD – равнобедренный =
= ABH =
ABH =  DCK = MX = YN,
DCK = MX = YN,
AH = KD т.к. MX и YN средние линии =
2MX = AH, 2YN = KD =
YN + MX = KD =
YN + MX + XY = HK + KD = 3.
3). Tg  =
=  = BH = HD · tg
= BH = HD · tg  = 3tg
= 3tg  .
.
4). tg =
= ; т.к.
; т.к.  cos
cos =
= =
= =
=
= BH = 3 ·  : (1
: (1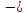
 ) = 9.
) = 9.
Ответ: 1 или 9.
Заключение.
Исследуя в своей работе многовариантные задачи, я пришёл к выводу, что решение задачи зависит от построения рисунка, отвечающего условиям задачи, а рисунок не всегда может выглядеть однозначно, поэтому нужно рассматривать разные изображения к данному условию.
Многовариантные задачи представляют чисто математический интерес, способствуют интеллектуальному развитию, служат хорошим материалом для отработки навыков анализа. Ценность их в том, что с их помощью можно проверить знание основных разделов математики, уровень математического и логического мышления, получить первоначальные навыки исследовательской деятельности.
Исследуя условия задач, я постарался ситематизировать эти задачи. Решая задачи, я повторил весь материал по планиметрии, изучил приемы решения многовариантных задач и рассмотрел задачи, которые редко встречаются в школьном курсе, а так же я познакомипся с формулами, которых нет в учебнике, например с формулой площади вписанного треугольника S =  .
.
Мне понравилось находить разные варианты построения рисунка и решения задач, к тому же данные задачи помогут мне критично относиться к задачам из других предметов, а так же задачам и проблемам, возникающих в жизни.
В своей работе в приложении я привёл ряд многовариантных задач, которые можно использовать на уроках для подготовки к ЕГЭ.
И, я надеюсь, что знания, которые я получил в процессе работы, помогут мне при сдаче Единого Государственного Экзамена и моя работа поможет моим одноклассникам лучше подготовиться к ЕГЭ.
Литература.
1. www.mathege.ru - Математика ЕГЭ 2010 (открытый банк заданий)
2. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010: Математика /авт.-сост. И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров и др.; под ред. А. Л. Семенова, И. В. Ященко. – М.: АСТ: Астрель, 2009. – (Федеральный институт педагогических измерений).
3. Справочник по математике, редактор А. З. Рыбкин. “Наука”, М. 1964 г. 608 стр. с илл.
Приложение.
Медианы треугольника
1. (2010) Медиана ВМ треугольника АВС равна его высоте АН. Найдите угол МВС.
Ответ: 30 или 150.
Высоты треугольника
2. (2010) Высоты треугольника ABC пересекаются в точке Н. Известно, что СН = АВ. Найдите угол АСВ.
Ответ: 45 или 135.
3. (2010) Точки А1, А2, А3 — основания высот треугольника ABC. Углы треугольника равны 90°, 60° и 30°. Найдите углы треугольника ABC.
Ответ: 45, 75, 60 или 135, 15, 30 или 120, 15, 45 или 105, 30, 45.
4. (2010) Точки D и E – основания высот непрямоугольного треугольника АВС, проведенных из вершин А и С соответственно. Извест-но, что  AB = b и BC = a. Найдите сторону АС.
AB = b и BC = a. Найдите сторону АС.
Ответ:  или
или 
Угол и окружность
5. (2010) На стороне АС угла ACВ, равного 45°, взята такая точка D, что СD = AD = 2. Найдите радиус окружности, проходящей через точки А и D и касающейся прямой ВС.
Ответ: 2 или .25
6. (2010) На стороне ВА угла ABC, равного 30°, взята такая точка D, что AD = 2 и BD = 1. Найдите радиус окружности, проходящей через точки А, D и касающейся прямой ВС.
Ответ: 1 или 7.
7. (2010) Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найдите радиус окружности, касающейся этой прямой и сторон угла.
Ответ: 1 или 6.
8. (2010) Прямая отсекает от сторон прямого угла отрезки 5 и 12. Найдите радиус окружности, касающейся этой прямой и сторон угла.
Ответ: 2 или 15.
Треугольник и окружность
9. (2010) Около треугольника ABC описана окружность с центром О, угол АОС равен 60°. В треугольник ABC вписана окружность с центром М. Найдите угол АМС.
Ответ: 105или 165 .
10. (2010) Треугольник ABC вписан в окружность радиуса 12. Известно, что АВ = 6 и ВС = 4. Найдите АС.
Ответ: .
.
11. (2010) В треугольнике ABC проведены высоты ВМ и CN, О — центр вписанной окружности. Известно, что ВС = 24, MN = 12. Найдите радиус окружности, описанной около треугольника ВОС.
Ответ: 8 или 24.
или 24.
12. (2010) Высоты треугольника АВС пересекаются в точке Н. Известно, что отрезок СН равен радиусу окружности, описанной около треугольника. Найдите угол АСВ.
Ответ: 60или 120.
13. (2010) Вершина равнобедренного треугольника с боковой стороной 5 и основанием 6 служит центром данной окружности радиуса 2. Найдите радиус окружности, касающейся данной и проходящей через концы основания треугольника.
Ответ:  или
или  .
.
14. (2010) Вершина равнобедренного треугольника с боковой стороной 5 и основанием 8 служит центром данной окружности радиуса 2. Найдите радиус окружности, касающейся данной и проходящей через концы основания треугольника.
Ответ:  или
или  .
.
Четырехугольники
15. (2010) В прямоугольнике ABCD АВ = 2, ВС =  . Точка Е на прямой АВ выбрана так, что
. Точка Е на прямой АВ выбрана так, что  AED =
AED = DEC. Найдите АЕ.
DEC. Найдите АЕ.
Ответ: 1 или 3.
16. (2010) В трапеции ABCD известны боковые стороны АВ = 27, CD = 28 и верхнее основание ВС = 5. Известно, что  = -
= -  . Найдите АС.
. Найдите АС.
Ответ: 28 или 2 .
.
17. (2010) Основания трапеции равны a и b. Прямая, параллельная основаниям, разбивает трапецию на две трапеции, площади которых относятся как 2:3. Найдите длину отрезка этой прямой, заключенного внутри трапеции.
Ответ: или .
18. (2010) Диагонали АС и BD трапеции ABCD пересекаются в точке Е. Найдите площадь трапеции, если площадь треугольника AED равна 9, а точка Е делит одну из диагоналей в отношении 1:3.
Ответ: 16; 48; 144.
Трапеция и окружность
19. (2010) Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту
Ответ: 39 или 9.
Непересекающиеся окружности
20. Найдите длину отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей равны 23 и 7, а расстояние между центрами окружностей равно 34.
Ответ: 30 или 16.
Касающиеся окружности
21. (2010) Окружности радиусов 4 и 9 касаются внешним образом, лежат по одну сторону от некоторой прямой и касаются этой прямой. Найдите радиус окружности, касающейся каждой из двух данных и той же прямой.
Ответ: 1,44 или 36.
Пересекающиеся окружности
22. (2010) Окружности радиусов 10 и 17 пересекаются в точках А и В. Найдите расстояние между центрами окружностей, если АВ = 16.
Ответ: 21 или 9.
1
 Содержание
Содержание


 , Точка Е на прямой АВ выбрана так, что
, Точка Е на прямой АВ выбрана так, что
 DC
DC
 2
2  3 = 1.
3 = 1.



 , окружность с центром
, окружность с центром