ОКРУЖНАЯ НАУЧНО – ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ
СЕКЦИЯ «Математика»
Алгебраический метод расстановки коэффициентов
в стехиометрических уравнениях
Автор: Богданова Светлана, ученица 9 класса
ГБОУ СОШ с. Бобровка.
ОУ: государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа с. Бобровка
муниципального района Кинельский Самарской области
Научный руководитель: Саликова Людмила Александровна, учитель математики.
Кинель 2014
Содержание
Введение
Обоснование и актуальность проблемы……………………………….. 2
Цель и задачи исследовательского проекта…………………………....2-3
Глава I.
Понятийный аппарат……………………………………………………3 - 4
Анализ источников информации по данной проблеме…………………. 4
2.1. Из истории……………………………………………………………....4
2.2. Правила составления уравнений…………………………………….4 - 5
Расстановка коэффициентов в уравнения……………………………5-7
Глава II.
1.Обоснование гипотезы и выводы……………………………………....7-11
Заключение………………………………………………………………….…..11
Библиография……………………………………...……………………............12
Введение
Обоснование и актуальность проблемы.
Математика – это язык, на котором говорят все точные науки.
Н.И. Лобачевский
Математика превратила химию из описательной науки в экспериментальную, и именно математика сделала химию наукой. С помощью математики мы производим расчёты по химическим формулам и решаем уравнения химических реакций, моделируем химические процессы как в живой, так и неживой природе. Без математики невозможно ни одно химическое производство. Если на мгновение представить, что было бы, если из химии исчезли числа и математические расчёты… Мир бы лишился пищи, лекарств, красок, фотоплёнок, минеральных удобрений, пластмасс, металлических сплавов и многих других полезных веществ и вещей.
Математика для химиков – это, в первую очередь, полезный инструмент решения многих химических задач. В школьном курсе химии при решении сложных уравнений окислительно-восстановительных реакций возникают большие трудностив расстановке коэффициентов.Так как очень трудно найти какой-либо раздел математики, который совсем не используется в химии, возникла мысль применить математические знания к разрешению химических проблем. Можно ли сопоставить уравнения в химии и математике? Существует ли иной, математический метод расстановки коэффициентов в химических уравнениях?Вот вопросы, которые побудили нас заняться исследованием данной проблемы. Изучить новый подход к решению химических задач, заинтересовать старшеклассников - веское доказательство актуальности данной работы.
2. Цель исследования:
изучить алгебраический метод расстановки коэффициентов в химических уравнениях и обосновать его применение к решению задач.
Задачи:
Изучить источники информации по данной теме.
Выявить приемы решения химических задач алгебраическим методом.
Показать использование алгебраического метода при решении химических уравненийокислительно-восстановительных реакций.
Составить алгоритм нахождения коэффициентов в химических уравнениях.
Объект исследования: окислительно-восстановительные уравнения химических реакций.
Методы исследования:теоретический анализ литературы по данной проблеме, сравнительный анализ, синтез, моделирование и обобщение.
Гипотеза: алгебраический метод решения уравнений химических реакций позволяет упростить процесс нахождения коэффициентов в уравнениях.
Теоретическая значимость исследования заключается в изучении алгебраического метода и его применении для решения задач, а практическая - состоит в возможности использования данного материала на уроках химии и при подготовке к ОГЭ и ЕГЭ.
Глава I
Понятийный аппарат
Химическим уравнением (уравнением химической реакции)1 - называют условную запись химической реакции с помощью химических формул, числовых коэффициентов и математических символов.
Стехиометрия2 (от др.-греч. στοιχεῖον «элемент» + μετρέω «измерять») - раздел химии о соотношениях реагентов в химических реакциях.
Реагенты3– химические препараты, предназначенные для химического анализа научно-исследовательских, различных лабораторных работ.
Закон сохранения массы4 гласит, что количество вещества каждого элемента до реакции равняется количеству вещества каждого элемента после реакции.
стехиометрическое уравнение5- уравнение, показывающее количественные соотношения реагентов и продуктов химической реакции.
коэффициенты6–натуральные числа, стоящие перед формулами веществ.
Анализ источников информации по данной проблеме.
Из истории.
История науки говорит о том, что на границах различных областей знания могут происходить очень интересные события. И хотя химики и математики мыслят совсем по-разному, те случаи, когда им удается взаимодействовать, приводят к появлению красивых и нетривиальных результатов и способствуют обогащению обеих наук.
В Конце XVIII — начале XIX вв.началось становлениезаконов стехиометрии.У истоков этих исследований стоял немецкий ученый И. В. Рихтер. В студенческие годы на него большое впечатление произвели слова его учителя - философа И. Канта о том, что в отдельных направлениях естественных наук истинной науки столько, сколько в ней математики Рихтер посвятил свою диссертацию использованию математики в химии. В своих научных работах Рихтер стремился отыскать математические зависимости в химических реакциях.Не будучи, в сущности, химиком, Рихтер ввел первые количественные уравнения химических реакций1,стал использовать термин стехиометрия2.
Рихтер посвятил свою диссертацию использованию математики в химии. В своих научных работах Рихтер стремился отыскать математические зависимости в химических реакциях.Не будучи, в сущности, химиком, Рихтер ввел первые количественные уравнения химических реакций1,стал использовать термин стехиометрия2.
Правила составления уравнений.
Уравнение химической реакции даёт качественную и количественную информацию о химической реакции, реагентах3 и продуктах реакции; его составление основывается на законе сохранения массы 4 веществ в химических реакциях
Составляя стехиометрическое уравнение5, вего левой части записывают формулывеществ, вступивших в реакцию, соединяя их знаком "плюс", а в правой части записывают формулыобразовавшихся веществ, также соединенных знаком "плюс". Между частями уравнения ставят стрелку. Получают схему реакции. Затем, используя закон сохранения массы веществ, находят коэффициенты6так, чтобы число атомов одинаковых элементов в левой и правой частях уравнения было равным
Чтобы превратитьсхему реакции в химическое уравнение, нужно подобрать коэффициенты для каждого вещества (в случаенеобходимости), записать их перед химическими формулами и заменить стрелку на знак равенства. Мы не ставим перед собой задачу научить составлять химические уравнения.Для того чтобы это сделать, нужно "совсем чуть-чуть" – знать свойства элементов.Практически же, даже высококвалифицированный химик не всегда "с ходу" может написать продукты реакции для данных исходныхвеществ.
Дальнейшее изложение относится только к ситуации, когда составленасхема реакции, т.е. известны формулы исходных веществ и продуктов, ноне известны стехиометрические коэффициенты в уравнении.
Расстановка коэффициентов в уравнениях.
Одним из способов уравнивания количества атомов в химическом уравнении является подбор коэффициентов методом проб и ошибок. В простых уравнениях реакций расстановка коэффициентов не вызывает большого затруднения: находится наименьшее общее кратное количества атомов и уравниваются правая и левая части. Сложно расставлять коэффициенты в уравнениях реакций, где число веществ, вступающих и образующихся в результате реакции более двух. В таких уравнениях подбор коэффициентов проводят методом электронного баланса, который носит не строго формализованный характер и имеет свои тонкости .
.
В ходе анализа источников информации по теме мы убедились, что существуети формально математический метод нахождениякоэффициентов, пригодный для разных химических реакций, которыйоснован на законе сохранения массы. Он называется алгебраическим. Наиболее подробно этот метод был изложен в записках профессора С. Г. Крапивина.
нахождениякоэффициентов, пригодный для разных химических реакций, которыйоснован на законе сохранения массы. Он называется алгебраическим. Наиболее подробно этот метод был изложен в записках профессора С. Г. Крапивина.
Оценивания алгебраический метод, профессор С.Г. Крапивин отмечает, что «все дело сводится к подсчету и комбинированию количеств атомов различных элементов для составления системы уравнений. Химическая сторона вопроса здесь не затрагивается» .
.
Для нахождения коэффициентов необходимо ввести неизвестные, при этом общее количество неизвестных должно равняться количеству реагирующих веществ. Затем, опираясь на число атомов каждого элемента, составляется система уравнений. Число уравнений в системе должно равняться числу химических элементов, участвующих в реакции .
.
Математические уравнения и методы, используемые в химии, имеют дело с конкретными свойствами атомов и молекул, которые подчиняются естественным природным ограничениям. Иногда эти ограничения бывают довольно жесткими и приводят к резкому сужению числа возможных решений математических уравнений. Математические уравнения, применяемые в химии, а также их решения должны иметь химический смысл. Поэтому на решения системы накладываются ограничения: решения системы должны быть натуральными и взаимно простыми .
.
Рассмотрим применение алгебраического метода на примере конкретной окислительно-восстановительной реакции, схема которой
HNO2 → HNO3 + NO + Н2О
Поставим в уравнение реакции коэффициенты в алгебраической форме,т.е. буквенные
aHNO2 = bHNO3 + cNO + dН2О
Опираясь на число атомов в каждом из соединений, составим систему уравнений материального баланса по каждому элементу (число атомов каждого элемента слева и справа от знака равенствадолжно быть одинаково):
a = b + 2d (баланс по водороду);
a = b + c (баланс по азоту);
2a = 3b + c + d (баланс по кислороду).
Таким образом, мы получили систему из 3 линейных уравнений с 4 неизвестными.

Решим систему линейных уравнений . Преобразуем уравнения таким образом, чтобы все коэффициенты были выражены через какой-либо один, например, c:
. Преобразуем уравнения таким образом, чтобы все коэффициенты были выражены через какой-либо один, например, c: 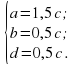
Используя требования натуральности коэффициентов и условие, что они должны быть взаимно простыми, нетрудно увидеть, что c=2, a = 3, b=1 и d=1. Итак, уравнение имеет вид:
3HNO2 = HNO3 + 2NO + Н2О
Проверка правильности расстановки коэффициентов в любом химическом уравнении производится подсчетом количества атомов кислорода, если в левой и правой части количество атомов кислорода одинаково, значит, коэффициенты расставлены правильно .
.
Глава II
1.Обоснование гипотезы.
Рассмотрим применение алгебраического метода для более сложных стехиометрических уравнений.
Пример1.
Составить уравнение реакции:Cu + HNO3 → Cu (NO3)2 + NO+ H2O
Расставляем алгебраические коэффициенты.
xCu +y HNO3 = z Cu (NO3)2 +m NO +n H2O
2.Опираясь на число атомов в каждом из этих соединений, составляем уравнения материального баланса.
3 y = 6 z + m + n (по кислороду)
y = 2z + m (по азоту)
x = z (по меди)
y= 2 n( по водороду)
3.Составляем систему уравнений.
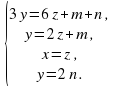
Заметим, что в полученной системе 4 уравнения и 5 неизвестных.
4.Выражаем все коэффициентычерез n.
Умножим второе уравнение на 3 и вычтем из первого, получим m = 0,5n.
Выразим из второго уравнения z, получим: z= = 0,75n.
= 0,75n.
Итак, 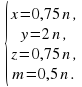
Очевидно, что для натуральных и "несокращаемых" коэффициентов n = 4, значит
x = 3, y = 8, z = 3, m = 2.
Окончательный вид уравнения:
3Cu +8 HNO3 = 3 Cu (NO3)2 +2 NO +4 H2O
Пример 2.
Составить уравнение реакции:
KMnO4 + HCl→ KCl + MnCl2 + Cl2 + H2O
Расставляем алгебраические коэффициенты.
aKMnO4 + bHCl = cKCl + dMnCl2 + eCl2 + fH2O
Составляем систему уравнений материального баланса по каждому элементу.
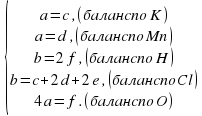
Заметим, что в полученной системе 5 уравнений и 6 неизвестных.
Выражаем все коэффициенты через а:
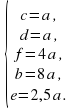
Получаем:
a=c=d=2; e=5; b=16; f=8.
Уравнение принимает вид:
2KMnO4+16HCl=2KCl+2MnCl2+5Cl2+8H2O.
Пример 3.
Составить уравнение реакции:
SnCl2 + HCl + KMnO4 → H2[SnCl6] + MnCl2 + KCl + H2О
Коэффициенты этого уравнения вряд ли можно легко подобрать, а вот
алгебраический метод нас не подведет.
1. Расставляем алгебраические коэффициенты
aSnCl2 + bHCl + cKMnO4 = dH2[SnCl6] + fMnCl2 + gKCl + hH2О.
2.Составляем систему уравнений материального баланса по каждому элементу.
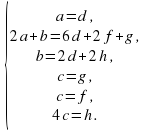
Заметим, что в полученной системе 6 уравнений и 7 неизвестных.
3.Теперь выражаем все коэффициенты через c:
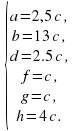
Очевидно, что для натуральных и "несокращаемых" коэффициентов
c=2, а=5, b=26, d=5, f=g=2, h=8.
Окончательный вид уравненияокислительно – восстановительной реакции:
5SnCl2 + 26HCl + 2KMnO4 = 5H2[SnCl6] + 2MnCl2 + 2KCl + 8H2O.
Рассматривая примеры, можно сделать вывод:если число уравнений материальногобаланса на единицу меньше числа коэффициентов, т.е. числа веществ, тоалгебраический метод позволяет однозначно находить коэффициенты, неприбегая ни к каким дополнительным соображениям.
Известны такие реакции, где число веществ меньше чем число входящих в них элементов . Рассмотрим такую реакцию.
. Рассмотрим такую реакцию.
Пример 4.
FeCl3+ KCNS → KCl+ Fe(CNS)3
Заметим, что группа атомов(CNS) переходит из одних веществ в другие, не изменяясь.
1.Расставляем алгебраические коэффициенты и составляем систему уравненийматериального баланса.
aFeCl3+ bKCNS= cKCl+ dFe(CNS)3
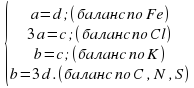 Мы видим, что уравнения по С,N, S повторяются.
Мы видим, что уравнения по С,N, S повторяются.
Отсюда 3a=b=c=3d, в простом случае a=d=1; b=c=3.
Получаем уравнение.
FeCl3+ 3KCNS = 3KCl+ Fe(CNS)3
Значит, алгебраический метод можно применять и к реакциям, где число веществ меньше чем число входящих в них элементов.
На основе проделанной работыможно составить алгоритм нахождения коэффициентов в стехиометрических уравнениях алгебраическим способом.
Для нахождения коэффициентов в стехиометрических уравнениях алгебраическим способом поступают следующим образом:
Обозначают все неизвестные коэффициенты переменными.
Составляют уравнения материального баланса, опираясь на число атомов в каждом из этих соединений.
Составляют систему линейных уравнений.
Решают полученную систему уравнений, выражая все коэффициенты через один из них.
Истолковывают результат, учитывая ограничения, применяемые в химии (решения системы должны быть натуральными и взаимно простыми).
Записывают получившееся уравнение.
Заключение
Данная работа предназначена для наиболее любознательного читателя. Проведенные исследования оказались важными и значимыми, так как с их помощью был найден новый прием решения стехиометрических уравнений.
В ходе исследований подтверждена истинность выдвинутой гипотезы: представленный алгебраический метод позволяет существенно упростить процесс нахождения коэффициентов в уравнениях химических реакций.Но этим методом может пользоваться лишь тот, кто владеет техникой решения систем линейных уравнений. Хочется надеяться, что данная работа окажет помощь учащимся 9,11 классов при подготовке к экзаменам, а также будет интересна всем тем, кто увлекается математикой.
Библиография
АбкинГ.Л., Методикарешениязадачпохимии.Пособиедляучителей. М., «Просвещение», 1971.
Берг Л.Г., Громаков С.Д.,Зороацкая И.В.,Аверко-Антонович И.Н. Способы подбора коэффициентов в химических уравнениях - Казань: изд-во Казанского ун-та, 1959.
Википедия — свободная энциклопедия. http://ru.wikipedia.org/
Габриелян О. С., Химия. 9 класс- М.: Дрофа, 2010.
Лиман М.М., Школьникам о математике и математиках: пособие для учащихся сред.школы.М.: Просвещение,1981.
Левицкий М. Язык химиков // Химия и жизнь. – 2000. –№1.
СрагоИ.А.,Окислительно-восстановительные реакции. Конспект лекций.http://window.edu.ru/library/
Цыпкин А.Г.,Пинский А.И., Справочное пособие по методам решения задач по математике. М.: «Наука»,1983
8

 Рихтер посвятил свою диссертацию использованию математики в химии. В своих научных работах Рихтер стремился отыскать математические зависимости в химических реакциях.Не будучи, в сущности, химиком, Рихтер ввел первые количественные уравнения химических реакций1,стал использовать термин стехиометрия2.
Рихтер посвятил свою диссертацию использованию математики в химии. В своих научных работах Рихтер стремился отыскать математические зависимости в химических реакциях.Не будучи, в сущности, химиком, Рихтер ввел первые количественные уравнения химических реакций1,стал использовать термин стехиометрия2.
 .
.  нахождениякоэффициентов, пригодный для разных химических реакций, которыйоснован на законе сохранения массы. Он называется алгебраическим. Наиболее подробно этот метод был изложен в записках профессора С. Г. Крапивина.
нахождениякоэффициентов, пригодный для разных химических реакций, которыйоснован на законе сохранения массы. Он называется алгебраическим. Наиболее подробно этот метод был изложен в записках профессора С. Г. Крапивина. .
.  .
.
 . Преобразуем уравнения таким образом, чтобы все коэффициенты были выражены через какой-либо один, например, c:
. Преобразуем уравнения таким образом, чтобы все коэффициенты были выражены через какой-либо один, например, c: 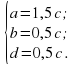
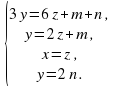
 = 0,75
= 0,75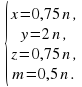
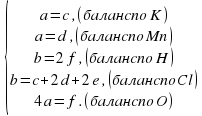
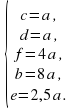
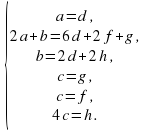
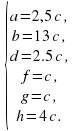
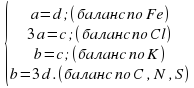 Мы видим, что уравнения по С,
Мы видим, что уравнения по С,




























