Тема проекта: Дроби вокруг нас
Тип проекта: исследовательский
Содержание
Введение 3
Теоретическая часть 5
1.1. История возникновения дробей 5
1.2. Интересные факты о дробях 8
2. Практическая часть 9
Заключение 13
Список литературы 14
Введение
В повседневной жизни мы часто сталкиваемся с такими понятиями, как половина, треть, четверть. С самого детства мы слышим такие выражения: «взять четверть яблока», «пройти половину пути», «одна вторая финала» или «три четверти часа». Во всех этих случаях мы говорим о дробях: одна четверть, две четверти, три четверти, одна вторая и треть - все это дроби. Мы пользуемся дробями с самого детства, не подозревая об этом: «Подайте, пожалуйста, мне половинку шоколадки», «Давай разделим апельсин поровну», «Я еще четверть часика поиграю с друзьями на улице», «Отрежьте, пожалуйста, полметра ткани» и т.п. Люди разных профессий используют дроби в процессе работы, даже не задумываясь об этом. Знания обыкновенных дробей и умения выполнять действия над ними необходимы людям в повседневной жизни.
В пятом классе на первом уроке математики при изучении дробей, я услышала такое крылатое выражение, которое сохранилось у немцев до сих пор – «попасть в дроби», что означает – попасть в трудное положение. В России есть аналогичное – «попасть в тупик». Рассуждение над значением этого фразеологизма привело меня к мысли о том, что работать с дробями действительно трудно. А позже, изучив, правила, по которым выполняются действия с дробями, до конца поняла смысл фразы.
Интересное и меткое «арифметическое» сравнение делал Лев Николаевич Толстой. Он говорил, что человек подобен дроби, числитель которой есть то, что человек представляет собой, а знаменатель – то, что он думает о себе. Чем большего мнения о себе человек, тем больше знаменатель, а значит, тем меньше дробь.
При выполнении работы я поставила перед собой следующую цель: показать, где применяются обыкновенные дроби в повседневной жизни человека.
Для этого мне пришлось решить задачи:
изучить литературу по данной теме;
проанализировать и исследовать полученную информацию;
рассмотреть применение дробей в повседневной жизни человека;
провести опрос среди учащихся гимназии;
выпустить газету в редакторе Microsoft Publisher.
1.Теоретическая часть
1.1. История возникновения дробей
В средние века, как и в древности, учение о дробях считалось самым трудным разделом арифметики. Римский оратор и писатель Цицерон говорил, что без знаний дробей никто не может признаваться знающим арифметику.
Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.
В русском языке слово "дробь" появилось лишь в VIII веке. Происходит слово "дробь" от слова "дробить, разбивать, ломать на части". У других народов название дроби также связано с глаголами "ломать", "разбивать", "раздроблять". В первых учебниках дроби назывались "ломанные числа". В старых руководствах находили следующие названия дробей на Руси:
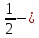 половина, полтина,
половина, полтина,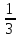 – треть,
– треть,
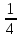 – четь,
– четь, 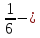 полтреть,
полтреть,
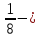 полчеть,
полчеть, 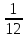 – полполтреть,
– полполтреть,
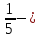 пятина,
пятина,
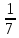 – седьмина,
– седьмина, 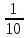 – десятина.
– десятина.
В Древнем Египте обозначали дроби не так, как обозначаем их мы: вверху – числитель, ниже черты – знаменатель.
У них черты дроби не было, специального общего для всех дробей способа обозначения не было. Египтяне употребляли только дроби с числителем единица. Они все дроби старались записать как суммы долей. Например, вместо 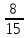 они писали
они писали  . Единственным исключением была дробь
. Единственным исключением была дробь 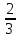 . Иногда это бывало удобно.
. Иногда это бывало удобно.
В папирусе Ахмеса есть задача: "Разделить 7 хлебов между 8 людьми". Если бы эту задачу стали решать ученики, то делили бы каждый хлеб на 8 частей, значит, пришлось бы сделать 49 разрезов. А по-египетски эта задача решалась так. Дробь 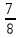 записывали в виде долей:
записывали в виде долей: 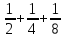 . Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезаем пополам, два хлеба - на 4 части и один хлеб - на 8 долей, после чего каждому даем его часть.
. Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезаем пополам, два хлеба - на 4 части и один хлеб - на 8 долей, после чего каждому даем его часть.
Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи.
Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков (к примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой). Максим Плануд греческий монах, ученый, математик в 13 веке ввел название числителя и знаменателя.
В Греции употреблялись наряду с единичными, «египетскими» дробями и общие обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним – числитель дроби. Например, 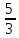 означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями. Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (
означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями. Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (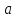 +b/c) или деление целого числа
+b/c) или деление целого числа 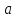 на дробь b/c. Правила действий над дробями почти не отличались от современных.
на дробь b/c. Правила действий над дробями почти не отличались от современных.
Записывать дроби как сейчас стали арабы. Средневековые арабы пользовались тремя системами записи дробей. Во-первых, на индийский манер записывая знаменатель под числителем; дробная черта появилась в конце XII – начале XIII в. Во-вторых, чиновники, землемеры, торговцы пользовались исчислением аликвотных дробей, похожим на египетское, при этом применялись дроби со знаменателями, не превышающими 10 (только для таких дробей арабский язык имеет специальные термины); часто использовались приближенные значения; арабские ученые работали над усовершенствованием этого исчисления. В-третьих, арабские ученые унаследовали вавилонско-греческую шестидесятеричную систему, в которой, как и греки, применяли алфавитную запись, распространив ее и на целые части.
Наряду с обыкновенными дробями используют десятичные дроби. Дроби записанные в форме 0,5; 0,34; 21,942; 7,2; 0,06 называют десятичными. Эту запись удобно использовать для всех дробей, у которых знаменатели равны 10, 100, 1000 и так далее.
При выполнении действий как с обыкновенными так и с десятичными дробями используют правила. Дроби можно сравнивать, складывать, вычитать, умножать и делить.
1.2. Интересные факты о дробях
Человек в жизни часто встречается со словом «дробь» и даже не задумывается над тем, что это слово изначально «математического происхождения».
Мелкие свинцовые шарики для стрельбы из охотничьего ружья называются дробью.
Частые, прерывистые звуки - барабанная дробь.
На флоте, команда «дробь!» — прекращение огня.
Номер через дробь ставят у домов, пронумерованных по двум пересекающимся улицам, например, 14/15.
В русском танце имеется весьма распространенный вид движений, выполняемых сильными, четкими, короткими и частыми ударами ног об пол. Танцующий как бы выстукивает ногами ритм танца. Такие движения русской пляски называются «дроби». Дроби весьма разнообразны по ритму и технике исполнения. В некоторых случаях дробь исполняется ударами поочередно одной и сразу же другой ногой в разных ритмических сочетаниях. Нога с каждым ударом опускается сильно и четко.
Современному человеку приходится есть буквально на ходу. Неудивительно, что в таких условиях большинство диетологов и врачей предлагают перейти на дробное питание, которое упорядочивает режим приёмов пищи и регулирует размер порций. Его в последнее время настолько расхвалили, что оно кажется чуть ли не единственно правильной системой, которая и похудеть позволяет, и самочувствие улучшает.
Фразеологизм «Выбивать дробь зубами – стучать зубами» означает дрожать от холода, испуга.
Главный герой рассказа Виктора Драгунского «Надо иметь чувство юмора» Дениска, задал однажды приятелю Мишке задачу: как разделить два яблока на троих поровну? И когда Мишка, наконец, сдался, торжествующе объявил ответ: «Сварить компот!» Мишка с Денисом ещё ничего не знали о дробях и думали, что 2 на 3 не делится
Практическая часть
Изучив литературу по истории возникновения дробей, мне захотелось провести небольшой опрос среди учащихся гимназии. Вопросы приведены ниже.
Опрос
Как Вы думаете, нужны ли современному человеку в жизни знания о дробях?
Используются ли дроби в профессиональной деятельности людей?
В каких профессиях чаще всего люди используют знания о дробях?
При изучении каких предметов в школе используются дроби?
Испытываете ли вы трудности при работе с дробями или действия с дробями выполняете безошибочно.
Опрос был проведен среди учащихся гимназии. В опросе приняли участие учащиеся 7Б класса в количестве 25 человек, 9В класса в количестве 14 человек и 10Б класса в количестве 21 человека.
Обработав данные опроса, получились следующие результаты: все учащиеся 9-х и 10-х классов утвердительно ответили на первый вопрос. А вот пять учащихся 7-х классов считают, что знания о дробях не нужны.
На второй вопрос все гимназисты, участвующие в опросе ответили, что дроби используются в профессиональной деятельности людей.
По третьему вопросу самыми популярными были профессии учителя, инженера, бухгалтера, продавца, экономиста, архитектора, врача, научного работника.
На четвертый вопрос список предметов выстроился по популярности ответов: математика, физика, информатика, химия, биология, технология, география.
Самыми интересными стали ответы на последний вопрос. При работе с дробями трудности испытывают 17 респондентов 7-го класса, 9 человек 9-го класса и 3 человека 10 класса. Вычислительные ошибки допускает половина семиклассников, 6 человек – учащихся 9-го класса. 12 человек 10 класса выполняют действия безошибочно.
Данные опроса позволяют сделать вывод, что тема «Дроби» действительно является сложной в школьной программе, так как испытывают трудности и делают ошибки даже десятиклассники. Здесь стоит отметить, что и для семиклассников эта тема не нова, а изучается уже третий год.
Проанализировав данные опроса, я решила собрать информацию о людях различных профессий, которые в своей деятельности используют дроби.
Информацию оформила в виде таблицы.
| № п/п | Направление деятельности | Как применяются дроби |
| 1
2 | Музыкант
Переплетчик | Ноты в музыке отличаются по длительности их звучания. Знаком обозначаю целую ноту, нота вдвое короче – половинная. Аналогично определяются четвертные, восьмые, шестнадцатые. 
Переплёты многих книг имеют отношение ширины и длины, близкое к значению 0,618. |
| 3 | Художник | 
|
| 4 | Географ | Участки земной поверхности изображаются на карте в уменьшенном виде, для этого используется понятие масштаба: отношение длины отрезка на карте к длине соответствующего отрезка на местности. Например: масштаб карты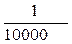 означает, что 1см на карте соответствует 10000см на местности. означает, что 1см на карте соответствует 10000см на местности. |
| 5 | Кулинар | Рецепт классических блинов Ингредиенты: Мука пшеничная — 1 стакан (или 130 грамм) Молоко — 1,5 стакана (300 мл) Яйца — 3 штуки Сахар — 1,5 ст. ложки Соль — 0,5 чайных ложки Масло сливочное — 40 грамм Количество порций: 16 |
| 6 | Врач - офтальмолог | 
|
| 7 | Продавец | Тенденция писать на ценниках цену не за килограмм, как это было раньше, а за 100 грамм появилась сравнительно недавно. Как утверждают эксперты тут скорее психологический момент и маркетинговый ход. В большинстве случаев цена за 100 грамм или 0,1 кг товара указана на сосиски, колбасы и колбасные изделия, сыры и конфеты. Это, как правило, достаточно дорогие продукты. |
| 8 | Банковский работник | В банковской сфере дроби имеют наибольшее значение при расчете ставок по кредитам и ипотеке. |
| 9 | Спортивный судья | В фигурном катании десятичные дроби применяются при выставлении оценок за исполненные элементы. Также выставляются баллы в художественной гимнастике. Метод отбора лучшего из лучших, идет еще древних времен, когда вообще начинались спортивные соревнования. Окончательным победителем признавался тот, у кого уже не оставалось достойных соперников. 1/2 финала, или полуфинал это борьба за второе место в первой тройке призовых. Тот, кто побеждает в полуфинале, выходит в финал. Четверть финала или 1/4 это соревнование за третье место. Тот, кто побеждает в четверть финале - выходит в полуфинал. Ну, а финал это понятно - кто в нем победит, тот будет чемпионом. |
| 10 | Учитель | Учитель. На уроке географии учитель спросил: «Какую часть земного шара покрывает вода?» Вода покрывает более 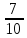 поверхности земного шара. «Какую часть от всех запасов воды составляет пресная вода?» По разным подсчётам доля пресной воды в общем количестве воды на Земле составляет 0,03. Около 0,87 запасов пресной воды содержится в виде льда. поверхности земного шара. «Какую часть от всех запасов воды составляет пресная вода?» По разным подсчётам доля пресной воды в общем количестве воды на Земле составляет 0,03. Около 0,87 запасов пресной воды содержится в виде льда. |
Заключение
Необходимость в дробях возникла на очень ранней ступени развития человека. В жизни человеку приходилось не только считать предметы, но и измерять величины. Люди измеряли длины, площади земельных участков, объемы, массы тел, время, вели расчеты за купленные или проданные товары. Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом. Так появились дроби и правила обращения с ними.
Изучив историю возникновения дробей, рассмотрев области их применения можно сделать вывод о том, что дроби нашли широкое применение в окружающей нас жизни и в различных науках. Значение дроби в жизни человека трудно переоценить. С их помощью строят дома, лечат людей, измеряют время, пишут музыку и шьют одежду…
Римский оратор Цицерон, живший в первом веке до нашей эры говорил: «Без знания дробей никто не может признаваться знающим арифметику!»
При выполнении работы я научилась проводить опрос, обрабатывать и анализировать полученную информацию. Также научилась оформлять информацию в таблицу. И работать в редакторе Microsoft Publisher.
Список литературы
Анищенко Е. А. Число как основное понятие математики. Мариуполь, 2002.
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 5 класс: учебник для общеобразовательных учреждений/- 26-е изд., стер. – М.: Мнемозина, 2009. - 280 с.
Гейзер Г.И. История математики в школе. Пособие для учителей. – М.: Просвещение, 1981. – 239 с.
Математика. 5 класс: учебник для общеобразовательных учреждений, СМ. Никольский, М.К.Потапов, Н.Н.Решетников, А.В. Шевкин. — 11-е изд.,— М.: Просвещение, 2016. — 272 с. — (МГУ — школе).
Математический энциклопедический словарь. – М., 1988.
http://pravorub. ru/articles/13039.html.
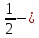 половина, полтина,
половина, полтина,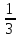 – треть,
– треть,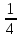 – четь,
– четь, 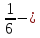 полтреть,
полтреть,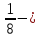 полчеть,
полчеть, 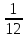 – полполтреть,
– полполтреть,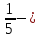 пятина,
пятина,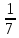 – седьмина,
– седьмина, 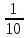 – десятина.
– десятина.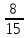 они писали
они писали  . Единственным исключением была дробь
. Единственным исключением была дробь 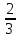 . Иногда это бывало удобно.
. Иногда это бывало удобно.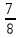 записывали в виде долей:
записывали в виде долей: 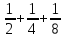 . Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезаем пополам, два хлеба - на 4 части и один хлеб - на 8 долей, после чего каждому даем его часть.
. Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезаем пополам, два хлеба - на 4 части и один хлеб - на 8 долей, после чего каждому даем его часть.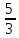 означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями. Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (
означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями. Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (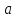 +b/c) или деление целого числа
+b/c) или деление целого числа 


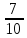 поверхности земного шара. «Какую часть от всех запасов воды составляет пресная вода?» По разным подсчётам доля пресной воды в общем количестве воды на Земле составляет 0,03. Около 0,87 запасов пресной воды содержится в виде льда.
поверхности земного шара. «Какую часть от всех запасов воды составляет пресная вода?» По разным подсчётам доля пресной воды в общем количестве воды на Земле составляет 0,03. Около 0,87 запасов пресной воды содержится в виде льда.















