ИНСТРУКЦИОННО – ТЕХНОЛОГИЧЕСКАЯ КАРТА
НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»
ТЕМА. Вычисление пределов. 1-ой и 2-ой замечательные пределы.
ЦЕЛЬ: научиться вычислять пределы функций.
ЗНАТЬ: теоремы о пределах, правила раскрытия неопределенностей вида: 0/0 и ∞/∞.
1-й и 2-й замечательные пределы.
УМЕТЬ: находить пределы функции, используя теоретические сведения.
НОРМА ВРЕМЕНИ: 2 часа.
ЛИТЕРАТУРА: Н.В. Богомолов «Практические занятия по математике» гл. 6, § 1.
ОБЕСПЕЧЕНИЕ ЗАНЯТИЯ: инструкционная карта, образцы решения типовых задач.
Просмотр содержимого документа
«Инструкционная карта к практической работе по теме Вычисление пределов. 1 и 2 замечательные пределы. »
Министерство образования и науки Самарской области
ГБОУ СПО «Безенчукский аграрный техникум»
РАССМОТРЕНО УТВЕРЖДАЮ
на заседании цикловой Зам. директора
комиссии учебной работе
естественно – научных и __________ С.А. Антонова
математических дисциплин «___» ___________ 200__г
протокол № __ от ________ 200__г.
Председатель ___________
ИНСТРУКЦИОННО – ТЕХНОЛОГИЧЕСКАЯ КАРТА
НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»
ТЕМА. Вычисление пределов. 1-ой и 2-ой замечательные пределы.
ЦЕЛЬ: научиться вычислять пределы функций.
ЗНАТЬ: теоремы о пределах, правила раскрытия неопределенностей вида: 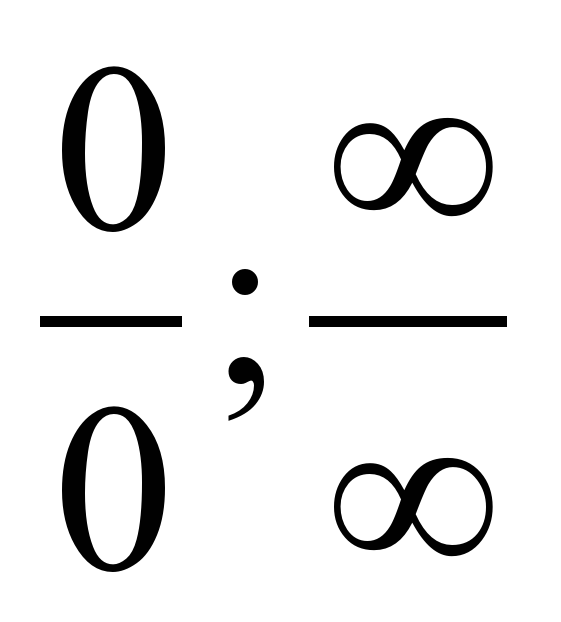 .
.
1-й и 2-й замечательные пределы.
УМЕТЬ: находить пределы функции, используя теоретические сведения.
НОРМА ВРЕМЕНИ: 2 часа.
ЛИТЕРАТУРА: Н.В. Богомолов «Практические занятия по математике» гл. 6, § 1.
ОБЕСПЕЧЕНИЕ ЗАНЯТИЯ: образцы решения типовых задач.
СОДЕРЖАНИЕ РАБОТЫ
И ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ
Задание 1. Повторите теорию, ответив на вопросы.
1). I Вариант II Вариант
1) Может ли при вычислении
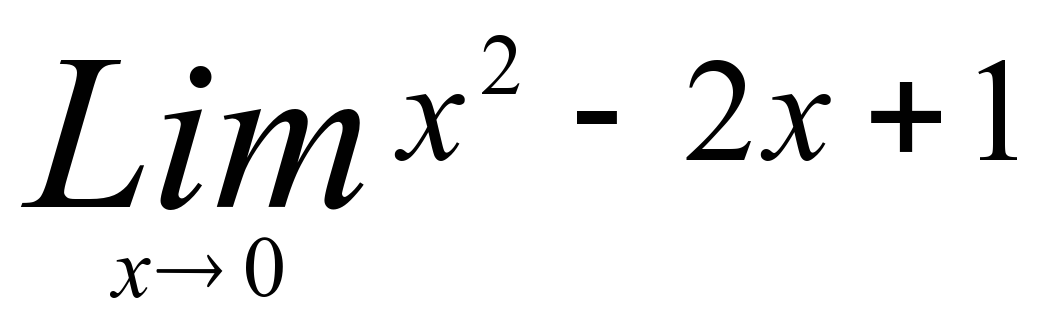
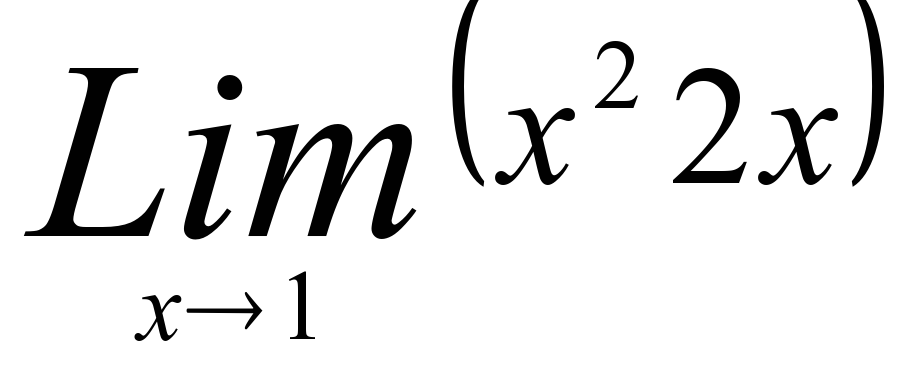
Получится ответ, содержащий х?
1) да 2) нет
2). Вставьте пропущенные знаки в теоремах о пределах.
Основные теоремы о пределах.
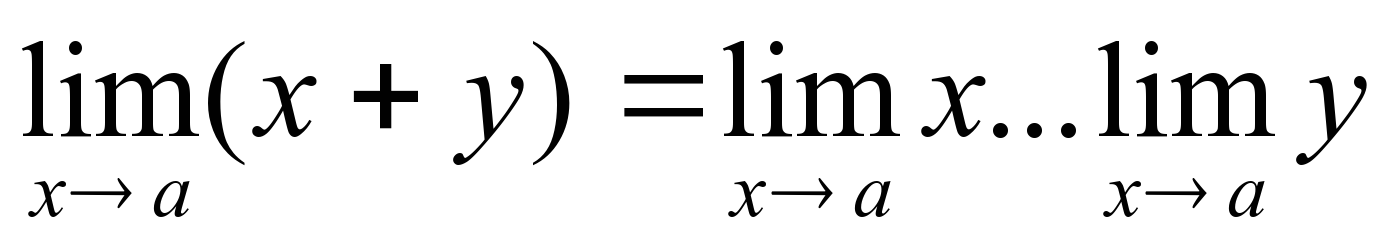
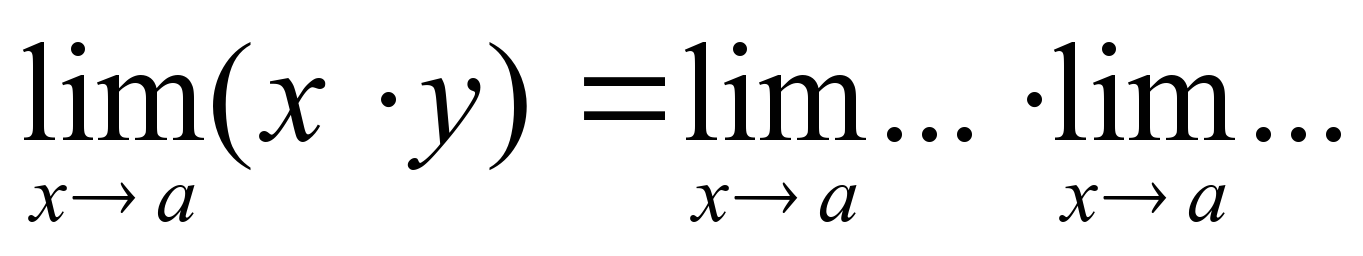
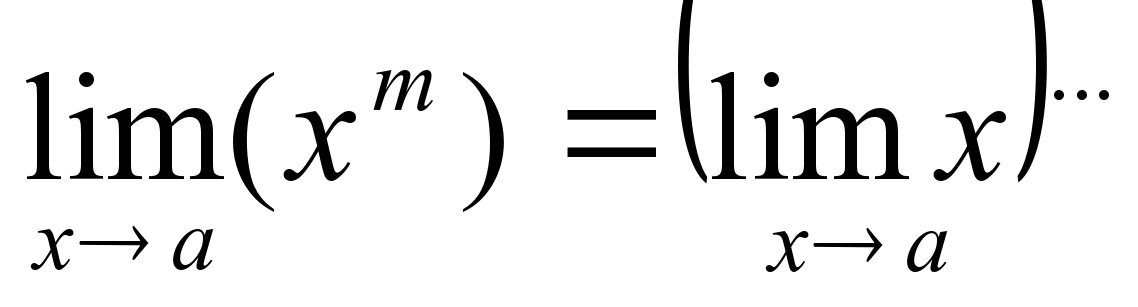
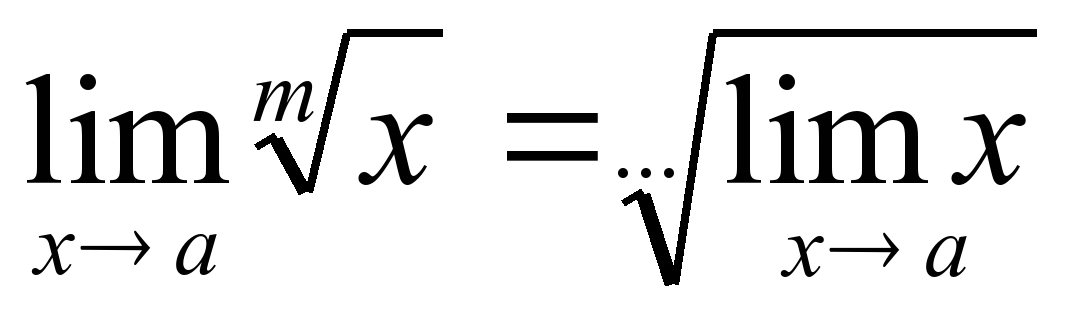
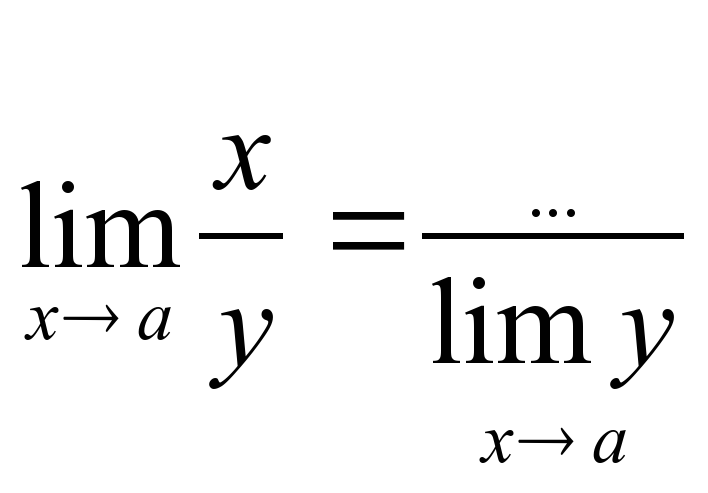 , если lim y≠0
, если lim y≠0
3). Заполните пропуски:
1. 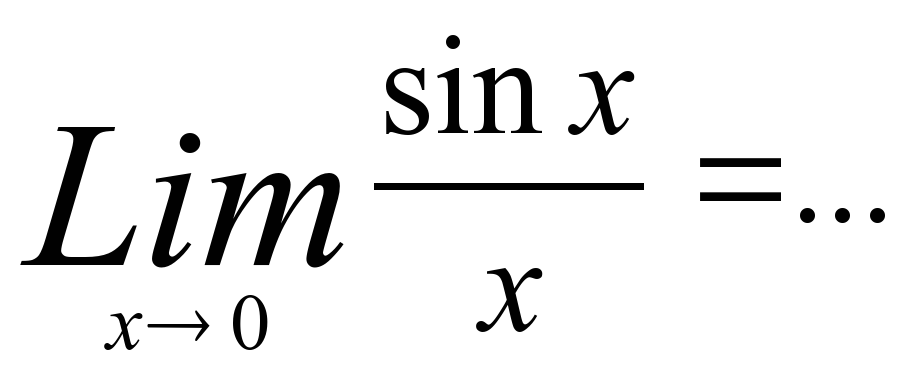 1- й замеч. предел. 2.
1- й замеч. предел. 2. 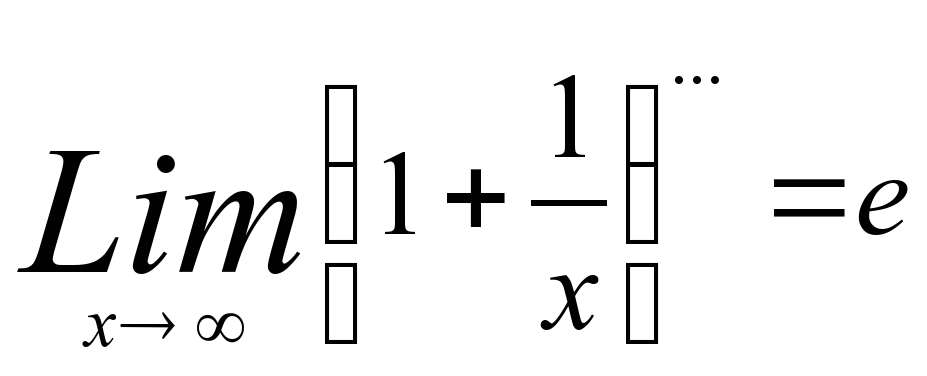 2-й замеч. предел.
2-й замеч. предел.
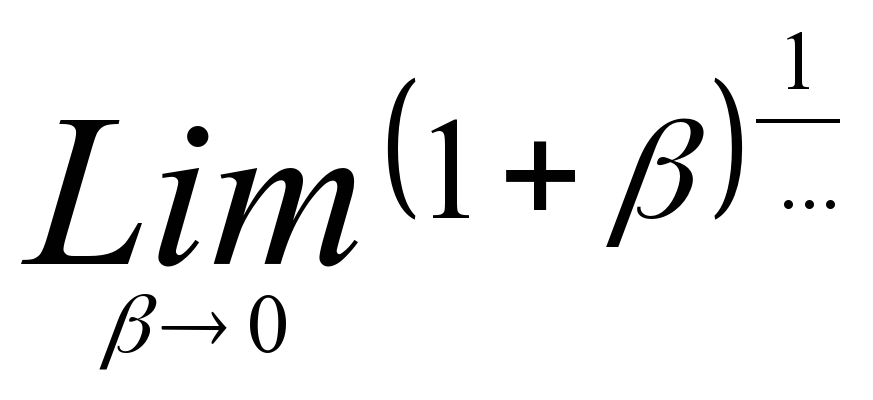 =e
=e
Ответы:
о; 1-й замечательный 1) х; е
1; 1-й замечательный 2) е; х
∞; 2-й замечательный 3) 1; 1
е; 2-й замечательный 4) ∞; е
Заполните пропуски:
| Величина, обратная бесконечно малой, есть … Ответы: бесконечно большая бесконечно малая число другой ответ | Является ли число 0,0001 – бесконечно малым? Ответы: да нет |
В каких точках х функция F(x) будет бесконечно малой?
| F(x)=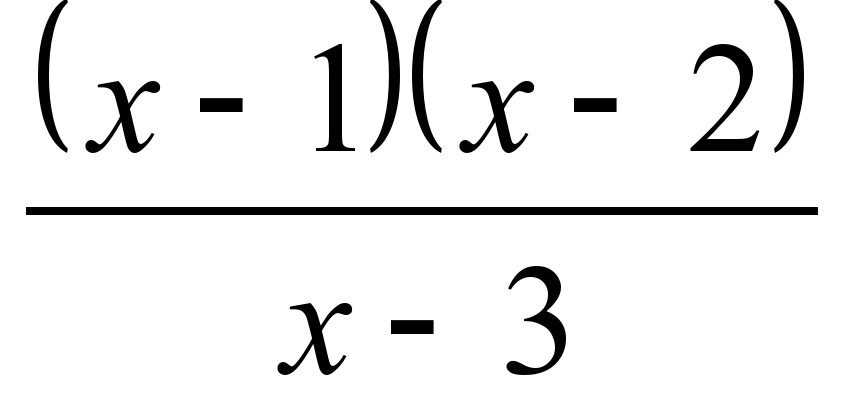 Ответы: х=3 х=1; х=2 х=1; х=2; х=3; х=0 х=1; х=3 | F(x)=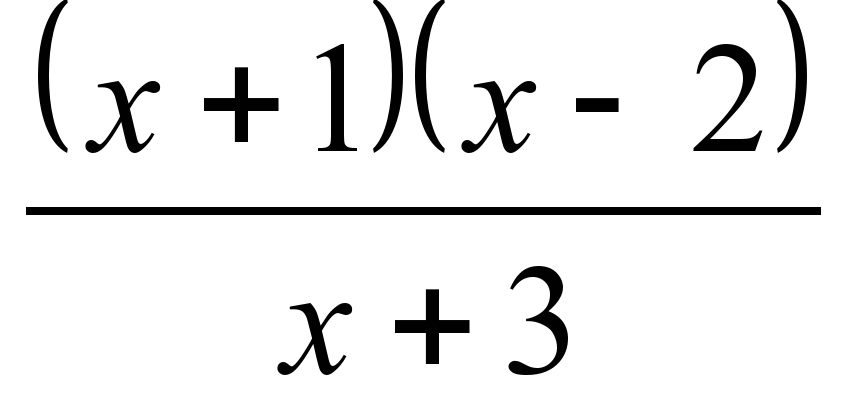 Ответы: х=-1; х=2 х=-3 х=-1; х=2; х=3; х=0 х=2; х=-3 |
Задание 2. Записать правила раскрытия неопределенностей вида 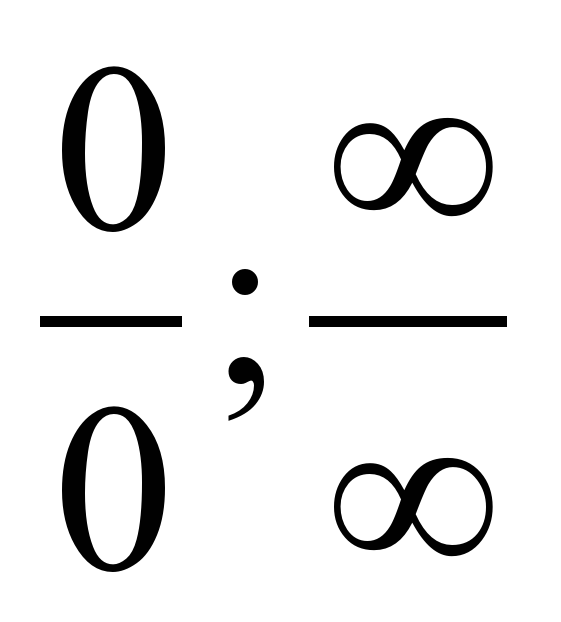 .
.
Разобрать решение типовых задач № 1, № 2 (устно).
ПРАВИЛО 1. Чтобы раскрыть неопределенность вида 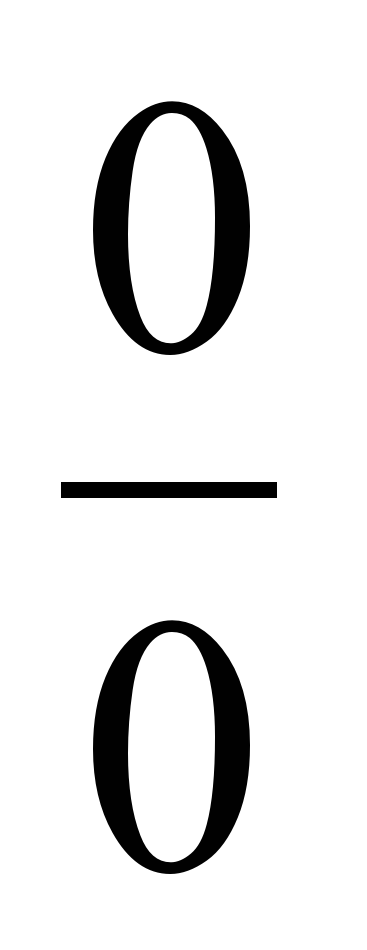 , надо числитель и знаменатель дроби разложить на множители с последующим сокращением.
, надо числитель и знаменатель дроби разложить на множители с последующим сокращением.
ПРИМЕР 1..Вычислить: 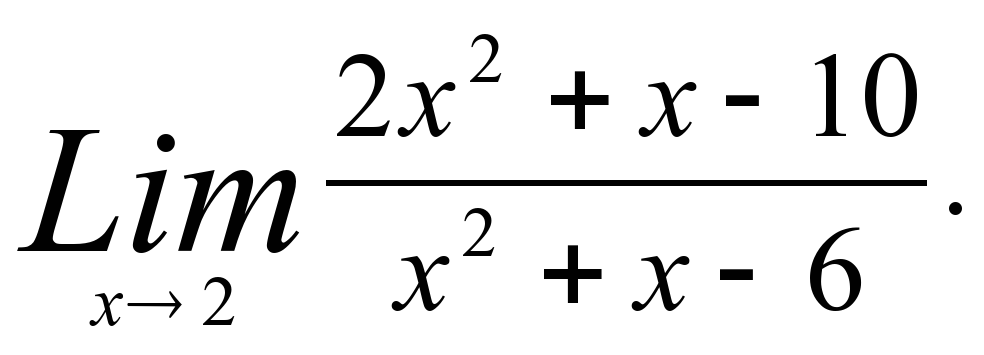
Решение. 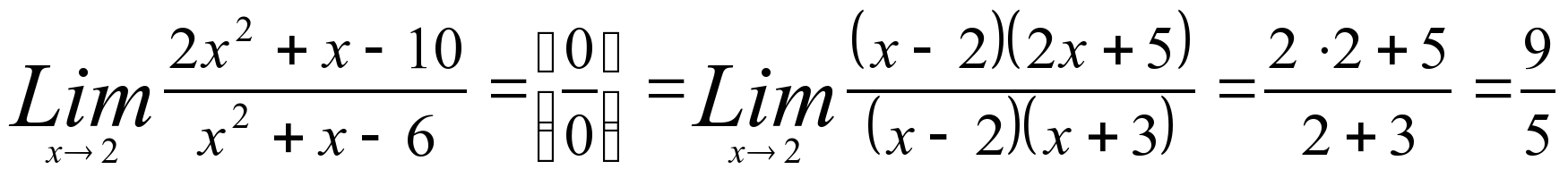 .
.
1) 2х2+х-10=0 2) х2+х-6=0
D=b2-4ac D=1-4∙(-6)=25
D=1-4∙2(-10)=81 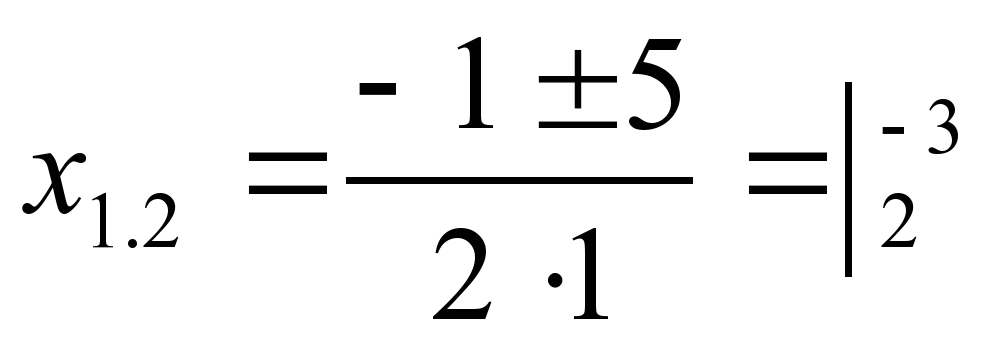
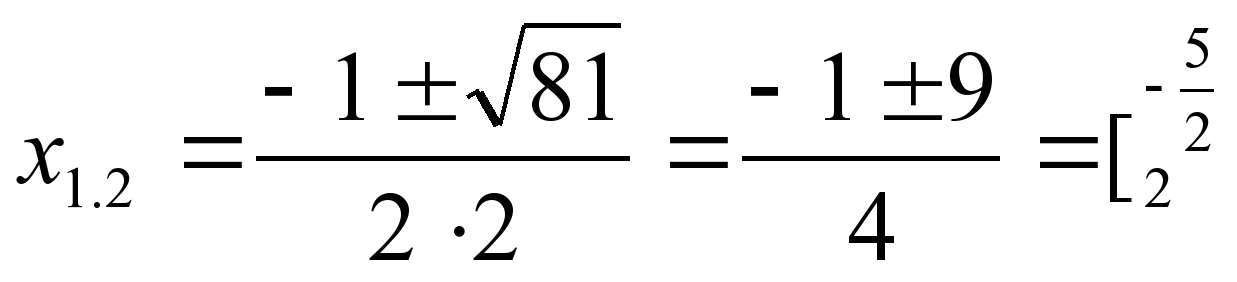 x2+x-6=(x-2)(x+3)
x2+x-6=(x-2)(x+3)
2x2+x-10=2(x-2)(x+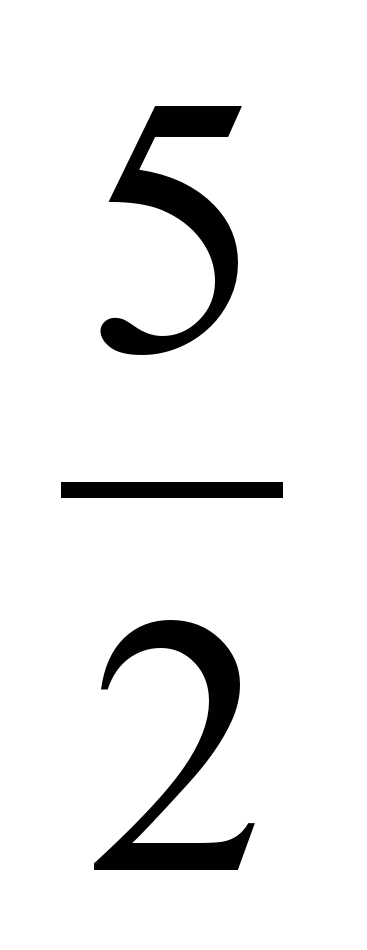 )=(x-2)(2x+5)
)=(x-2)(2x+5)
Заметим, что х 2, но не равен 2, следовательно, множитель, на который сокращаем (х-2), отличен от нуля при х2
ПРАВИЛО 2: Чтобы раскрыть неопределенность вида  , надо числитель и знаменатель дроби разделить на старшую степень неизвестного.
, надо числитель и знаменатель дроби разделить на старшую степень неизвестного.
ПРИМЕР 2. Вычислить: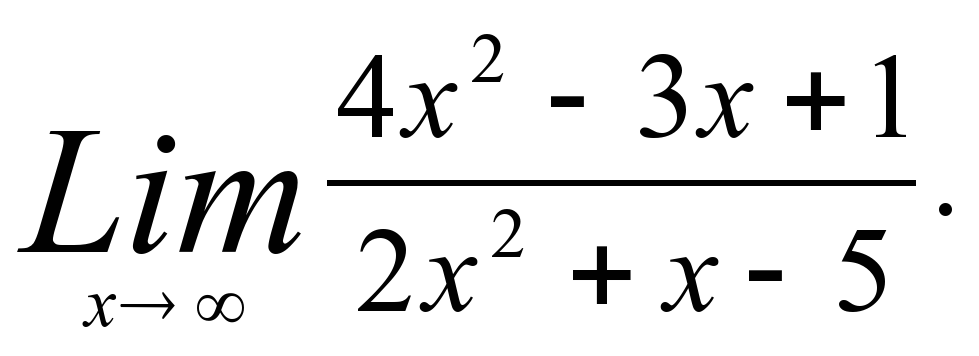
Решение. 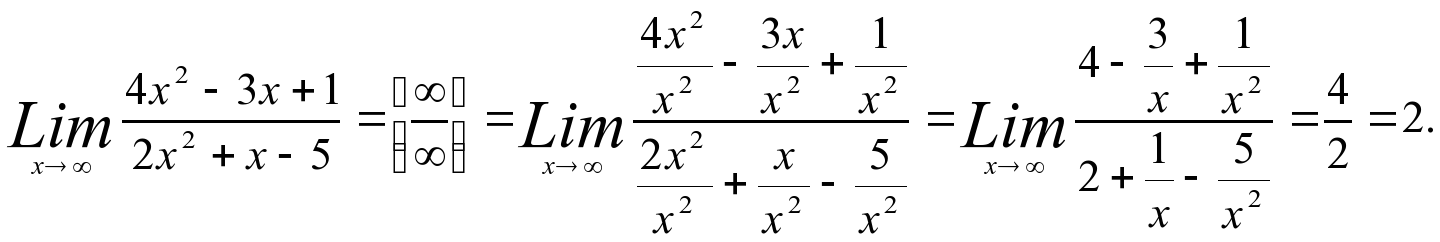
Задание 3. Вычислить пределы функций.
1) 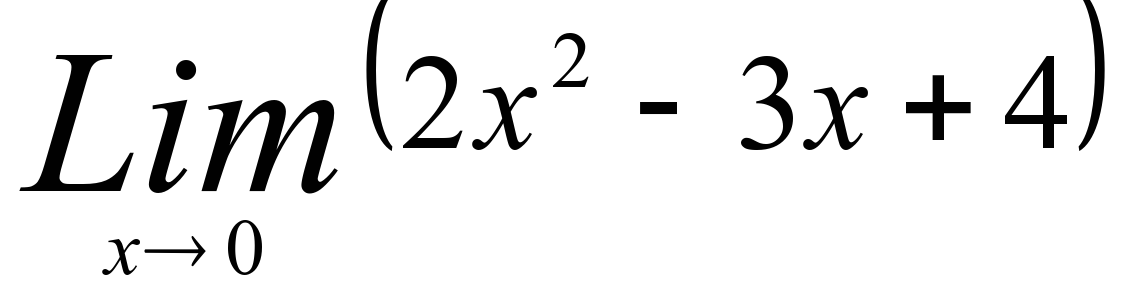 5)
5) 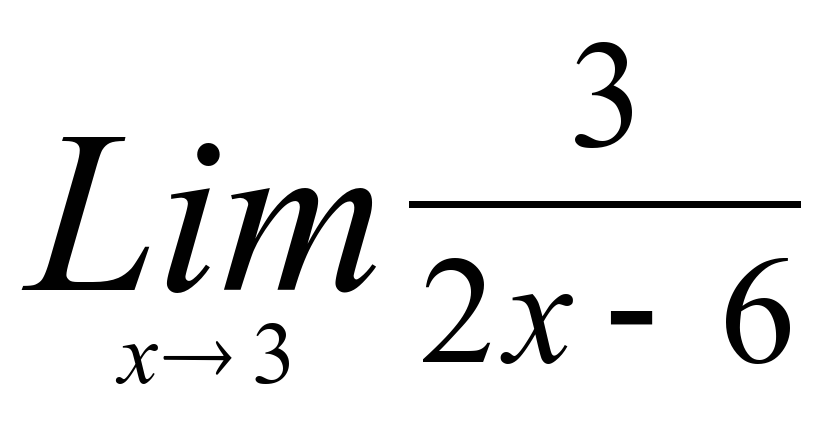 9)
9) 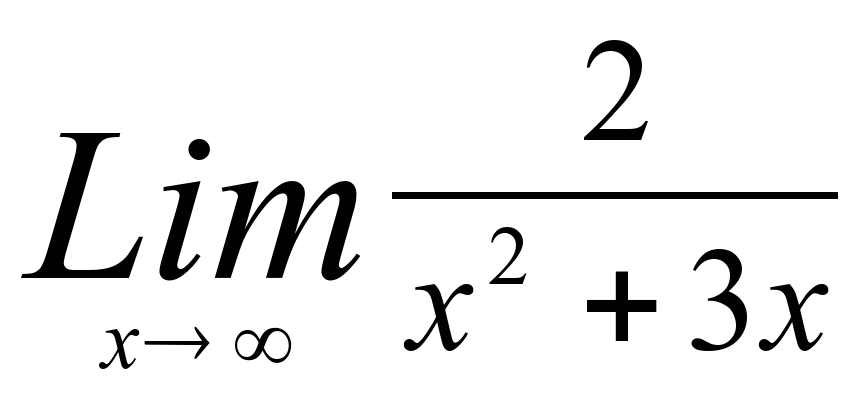
2) 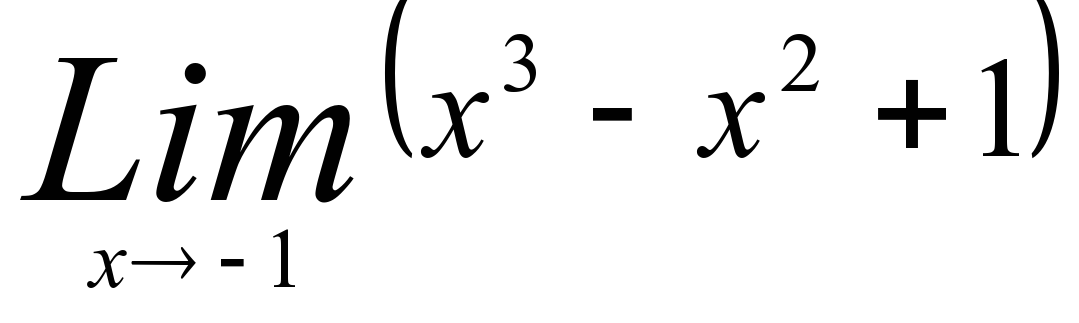 6)
6) 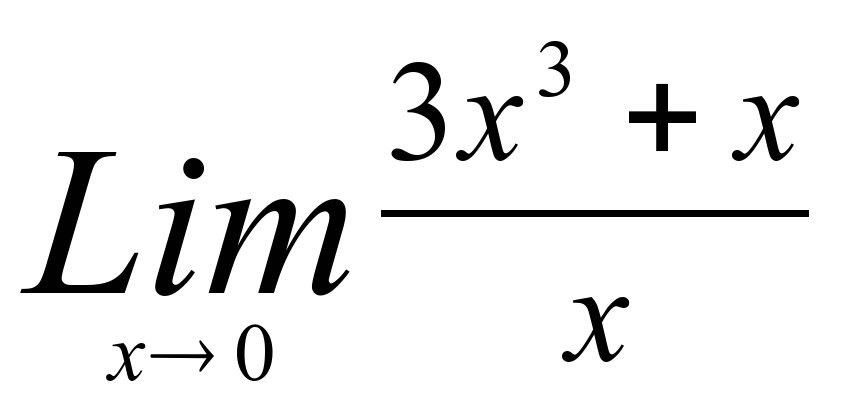 10)
10) 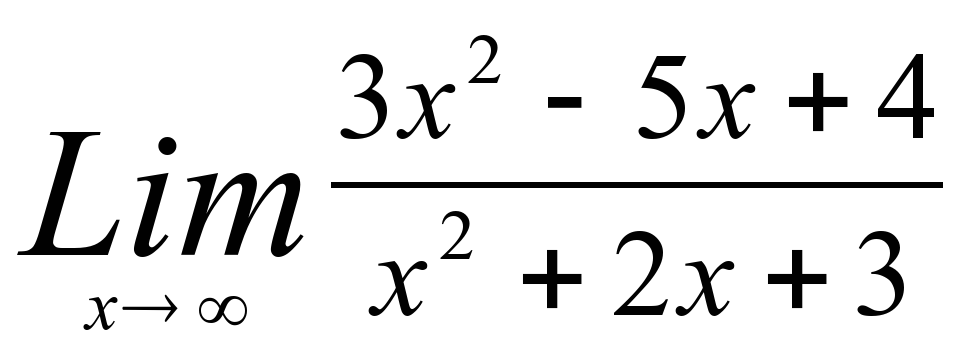
3) 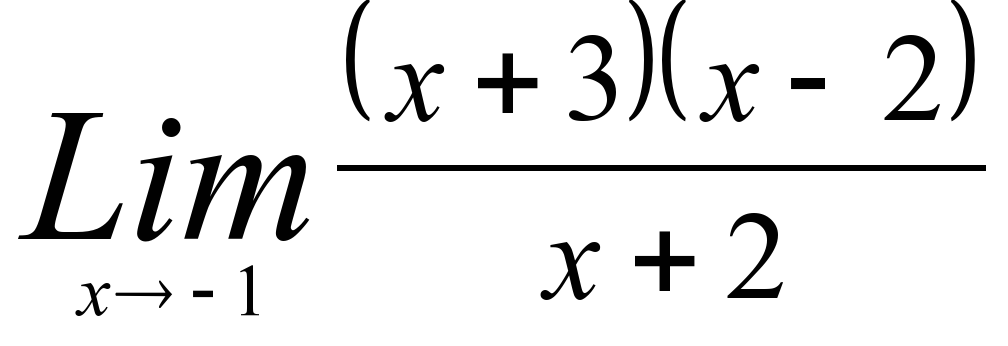 7)
7) 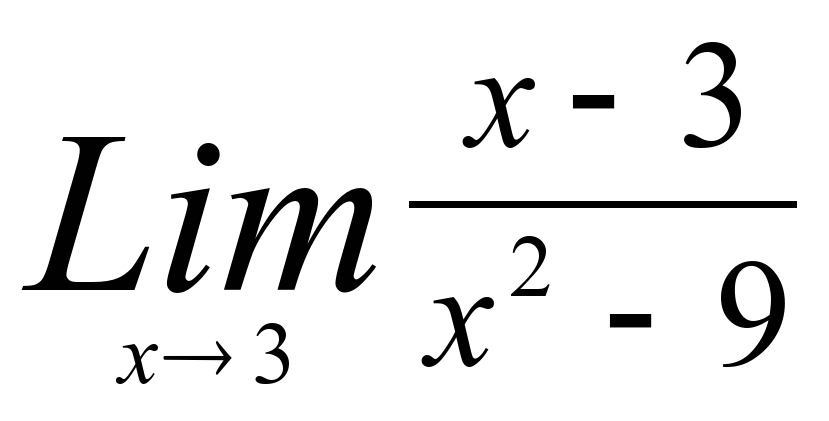 *11)
*11) 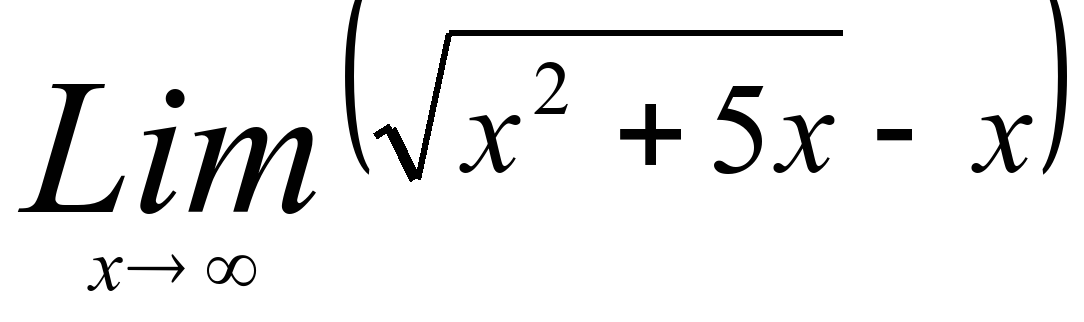 .
.
4) 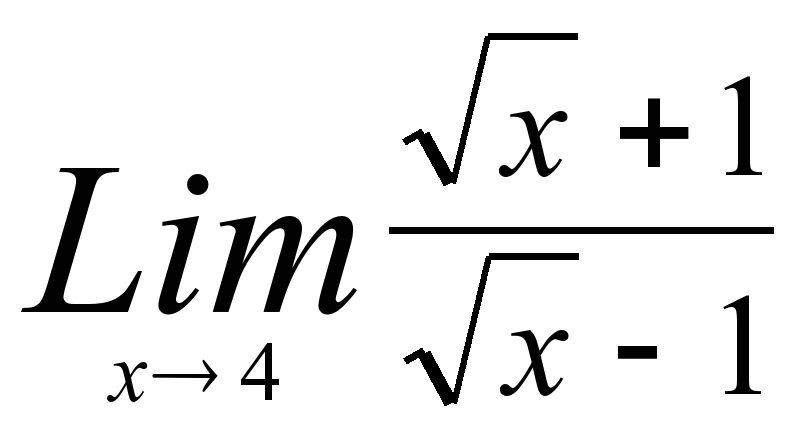 8)
8) 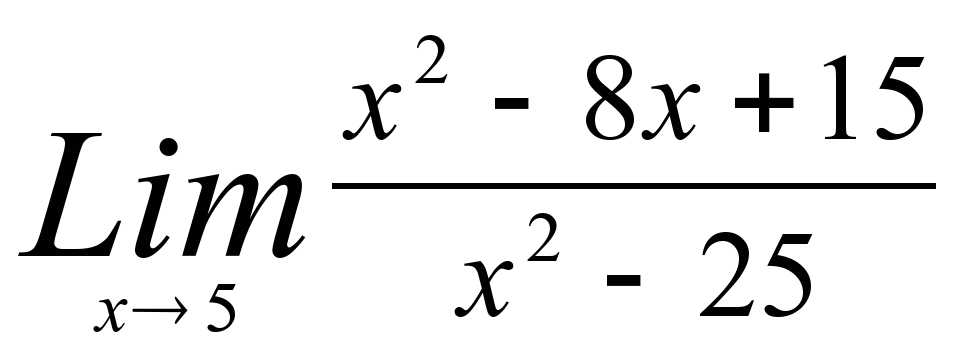
Ответы. 1) 4 5) ∞ 9) 0
2) -1 6) 1 10) 3
3) -6 7) 1/6 11) 5/2
4) 3 8) 1/5
4. Домашнее задание. Вычислить:
1) 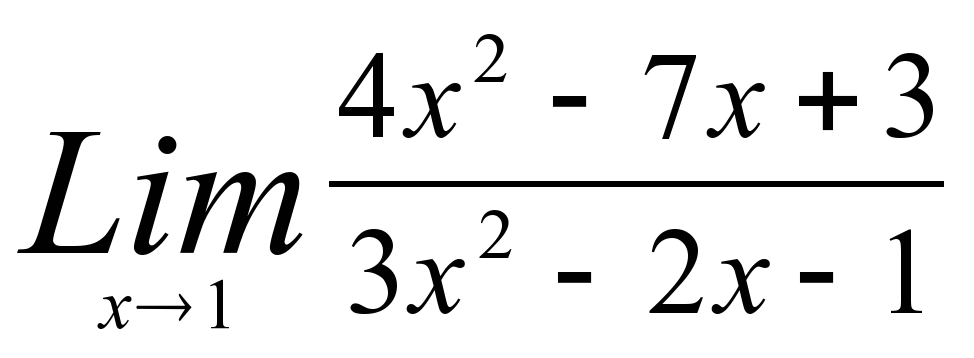 1)
1) 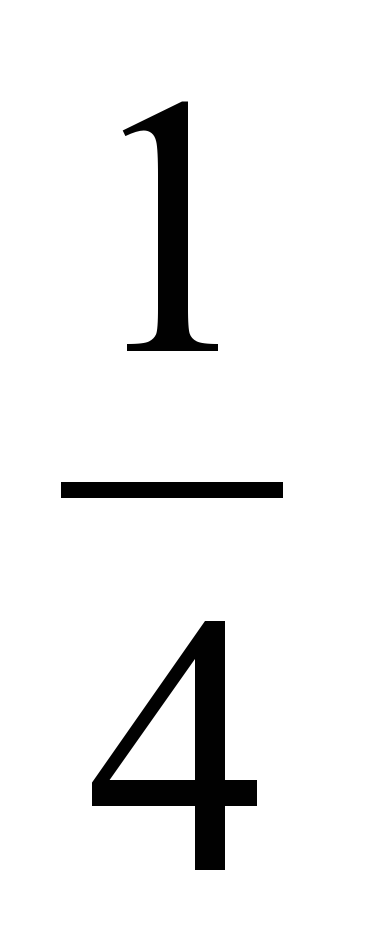
2) 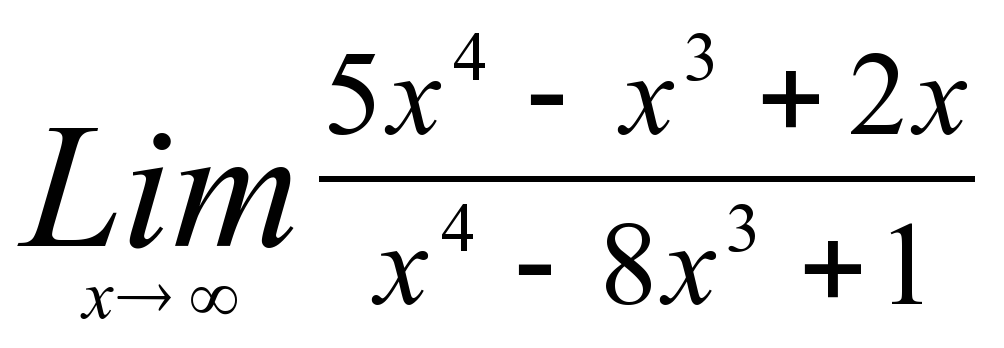 2) 5
2) 5
3) 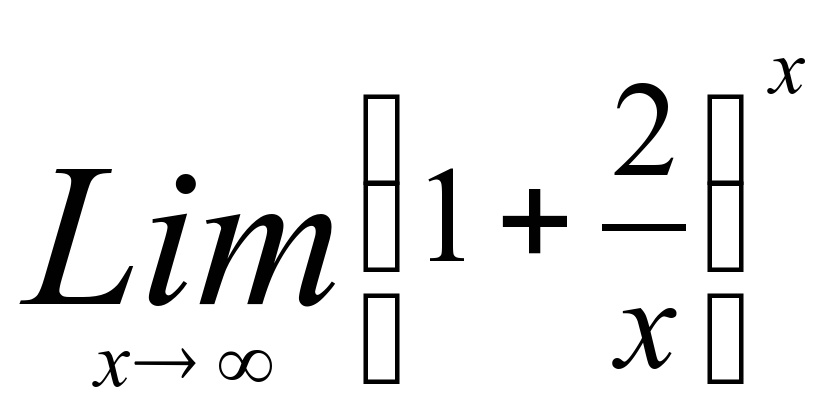 3) е2
3) е2
4) 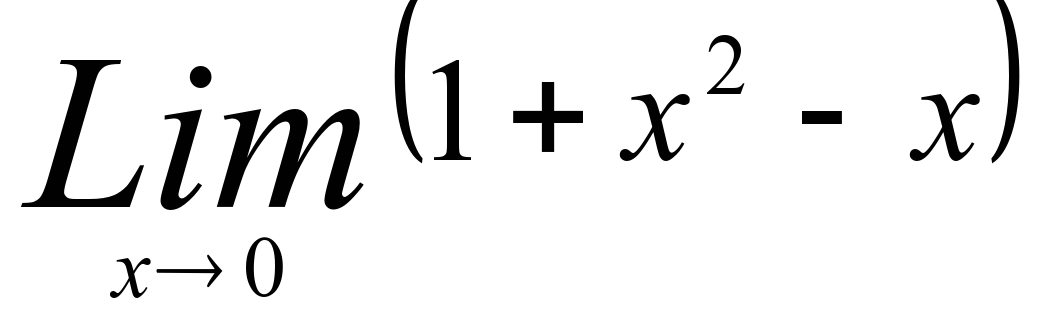 4) 1
4) 1
5) 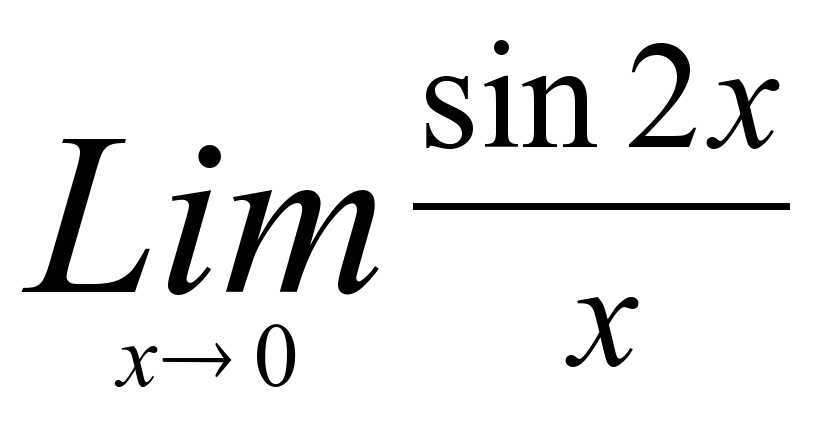 5) 2
5) 2
Преподаватель: ________________ Большакова Т.Л.
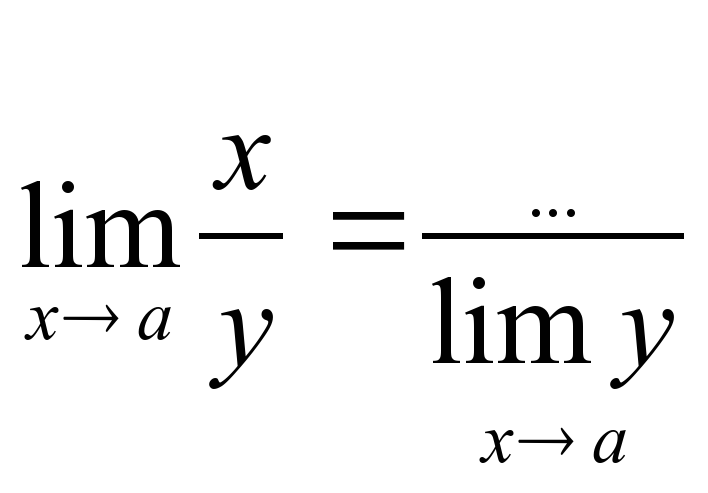 , если lim y≠0
, если lim y≠0