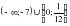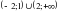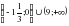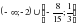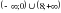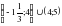Итоговая контрольная работа разработана на основе рабочей программы Федерального государственного стандарта среднего профессионального образования по профессии 35.01.14 Мастер по техническому обслуживанию и ремонту машинно - тракторного парка, утвержденной приказом Министерства образования и науки РФ от «02» августа 2013 г. № 709.
Содержание контрольной работы соответствует требованиям к освоению студентами основной профессиональной образовательной программы дисциплины «Математика» по профессии 35.01.14 Мастер по техническому обслуживанию и ремонту машинно-тракторного парка ФГОС СПО третьего поколения.
Экзаменационная работа по дисциплине «Математика» состоит из 10 заданий. Уровень сложности заданий определяется требованиями к математической подготовке обучающихся по профессии «Мастер по техническому обслуживанию и ремонту машинно-тракторного парка» в системе профессионального образования. Задания работы полностью соответствуют разделам программы дисциплины «Математика».
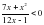
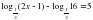
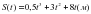 , где t – время движения в секундах. Найти скорость и ускорения через 2 секунды после начала движения. Определить характер движения по результату решения.
, где t – время движения в секундах. Найти скорость и ускорения через 2 секунды после начала движения. Определить характер движения по результату решения.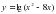
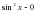 ,25 = 0
,25 = 0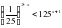
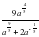 при а = 5
при а = 5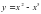 , х = 0, х = 1 и осью Ох.
, х = 0, х = 1 и осью Ох.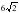 см. Найти площадь полной поверхности цилиндра и его объем.
см. Найти площадь полной поверхности цилиндра и его объем.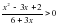
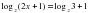
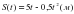 , где t – время движения в секундах. Найти скорость и ускорения через 4 секунды после начала движения. Определить характер движения по результату решения.
, где t – время движения в секундах. Найти скорость и ускорения через 4 секунды после начала движения. Определить характер движения по результату решения.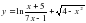
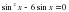
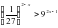
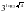
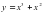 , х = 1, х = 2 и осью Ох.
, х = 1, х = 2 и осью Ох.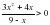
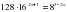
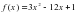 на интервале
на интервале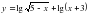
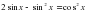
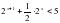
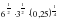
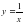 , х = 1, х = 2 и осью Ох.
, х = 1, х = 2 и осью Ох.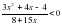
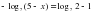
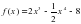
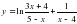
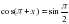 , если x[0; 2]
, если x[0; 2]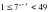
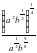 при а = 7 и b = 2
при а = 7 и b = 2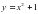 , х = 0, х = 2 и осью Ох.
, х = 0, х = 2 и осью Ох.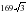 см2. Найти ребро тетраэдра и его объем.
см2. Найти ребро тетраэдра и его объем.