Тарасова С. А.
«Математические задачи в литературных произведениях»
Содержание
Введение………………………………………………………………………….2
1. Математика в стихах………………………………………………………….4
2. Задачи в художественных произведениях……………………………….….8
3. Задачи Льва Николаевича Толстого………………………………………...15
4. Заключение…………………………………………………………………...18
Литература ……………………………………………………………………...19
«Математика и литература –
Две ветви человеческой культуры,
Две книги из одной библиотеки,
Две песни из единой фонотеки.
Такие разные, как буква и число,
Неразделимые, как лодка и весло.
Что их роднит, объединяет в вечность?
Великой мысли дух и бесконечность!»
А. Лихолет о Н.И.Лобачевском
Введение
Хорошие книги можно читать по – разному « залпом», едва поспевая за увлекательно разворачивающимся сюжетом или медленно, наслаждаясь красотой авторского слога. А еще можно читать глазами математика, замечая и анализируя забавные ситуации. И это не только увлекательное, но и поучительное занятие.
Часто можно услышать такую фразу: «Ой, да что эта математика! Сухая наука. Выучил формулу — и решай задачи! Не то, что литература. Вот где красота и гармония». Да, так говорят многие. Но они забывают о том, что именно математика подарила нам такие слова как гармония, симметрия, пропорция. Каждому искусству присуще стремление к стройности, соразмерности, гармонии.
Я нередко встречаюсь с употреблением математических данных и числительных в художественных текстах .Какова же роль числительных в тексте? Часто задумываюсь,а данные используются с достоверной точностью или просто так « к слову»? На эти вопросы я попыталась ответить, проанализировав некоторые отрывки литературных произведений.
Данная работа посвящена двум самым известным, и, казалось бы, ничем не связанным между собой наукам: математике и литературе. В связи с этим были поставлены следующие цели и задачи:
Цель:
установить связь между математикой и литературой
Задачи:
Используя, знания по математике проанализировать точность использования математических данных в тексте
Раскрыть эстетический потенциал математики;
Найти материалы, подтверждающие связь между литературой и математикой;
Использовать исторические сведения межпредметного характера;
Доказать присутствие математики в литературе.
Для многих моих ровесников математика и литература - как планеты из разных галактик, не связанные между собой. Ребята стали мало читать. Для того, чтобы стимулировать интерес к художественной литературе необходимо использовать литературные произведения на уроках математики, это оживит процесс обучения и повысит интерес учеников к предмету, даст им понимание тесной взаимосвязи между разными науками, улучшит письменную и устную речь.
Математика в стихах
В эпоху античности уровень развития математики был очень высок. Греки использовали накопленные в Вавилонии и Египте арифметические и геометрические знания. В результате самостоятельного развития, а также на основе определённого запаса знаний, заимствованных у вавилонян и египтян, математика превратилась в особую научную дисциплину, основанную на дедуктивном методе.
Значение индийской науки для Запада невозможно переоценить. Большинство великих открытий и изобретений, которыми гордится Европа, были бы невозможны без созданной в Индии математической системы. Если говорить о влиянии, которое оказал на мировую историю неизвестный математик, изобретший новую систему, и о его аналитическом даре, его можно считать самым значительным после Будды человеком, которого когда-либо знала Индия. Средневековые индийские математики, такие как Брахмагупта (VII в.), Махавира (IX в.), Бхаскара (XII в.), в свою очередь, сделали открытия, которые стали известны в Европе только в эпоху Ренессанса и позднее. Они оперировали положительными и отрицательными величинами, изобрели изящные способы извлечения квадратного и кубического корней, они умели решать квадратные уравнения и некоторые типы неопределенных уравнений.
Есть древняя задача про лотос на теорему Пифагора.
Вот условие:
«Над озером тихим,
С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Воле цветка над водой,
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода
Здесь глубока?»
Обозначим глубину пруда через х, тогда высота лотоса будет (х+4). Когда подул ветер, высота лотоса превратилась в гипотенузу прямоугольного треугольника, одна из сторон которого х (глубина пруда), другая - 16.
По теореме Пифагора:
х2 + 22 = (x + 0,5)2
x2 + 4 = x2 + x + 0,25
x=4 - 0,25
x=3,75.
Сильное впечатление производит использование оригинальных формулировок задач, теорем, доказательств, известных из истории. Античные ученые часто составляли задачи в стихотворной форме.
Вот пример, древнеиндийская задача:
«Есть кадамба-цветок.
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда,
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи,
На кутай этих пчел посади.
Лишь одна не нашла
Себе места нигде,
Все летала то взад, то вперед и везде
Ароматом цветом наслаждалась.
Назови теперь мне, подсчитавши в уме,
Сколько пчелок всего здесь собралось?»
Данная задача имеет несколько способов решения
1 способ.
Пусть всего собралось Х пчелок, тогда имеем уравнение:
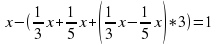
Решив это уравнение, получим ответ: 15 пчел.
2 способ
Наиболее значительный вклад в развитие античной математики на заключительном этапе внёс Диофант. Использовав, видимо, данные египетских и вавилонских математиков, он продолжил разработку методов алгебраических исчислений. Наряду с усилением религиозно-мистического интереса к числам продолжалась также разработка подлинной теории чисел.
Известный ученый Диофант жил в III веке, остальные известные факты его биографии исчерпываются таким стихотворением – загадкой, по преданию выгравированным на его надгробии:
«Путник! Здесь прах погребен Диофанта,
И числа поведать могут, о чудо, сколь долг был век его жизни.
Часть шестую его представляло счастливое детство.
Двенадцатая часть протекла еще жизни –
Пухом покрылся тогда подбородок.
Седьмую в бездетном браке провел Диофант.
Прошло пятилетье.
Он был осчастливлен рожденьем прекрасного первенца сына,
Коему рок половину лишь жизни счастливой и светлой
Дал на земле по сравненью с отцом.
И в печали глубокой старец земного удела конец воспринял,
Переживши года четыре с тех пор, как сына лишился.
Скажи, скольких лет жизни достигнув,
Смерть воспринял Диофант?»
Составим и решим уравнение:
Пусть Диофант прожил x лет. Составим и решим уравнение:
x/6+x/12+x/7+5+x/2+4=x
Умножим уравнение на 84, чтобы избавиться от дробей:
14x+7x+12x+420+42x+336=84x
-9x=-756
x=84
Оказывается, в 84 года.
Задачи в художественных произведениях разных авторов
В некоторых художественных произведениях встречаются математические задачи. Эти задачи ставят перед читателями авторы некоторых романов, повестей, рассказов, как правило, между — делом зачастую сами не обращая на это внимания. А сами авторы часто рассматривают математическую задачу как деталь, фон, эпизод своего повествования. Но были писатели, которые серьезно интересовались математикой и придумали немало интересных задач. Если читатель любитель математики, от него такая задача не ускользнет! Он не упустит случая разобраться, что это там предложил автор: разрешима задача или нет, сколько решений, можно ли обобщить и т.п. Иногда автор бывает столь любезен, что вместе с условием задачи приводит и решение. Но это явление редкое. Чаще дается лишь условие. Перейдем к конкретным примерам.
Задача № 1.
Л. Кассиль «Кондуит и Швамбрания» кн. 2, гл. « Задача с путешественниками».
Из двух городов выезжают по одному направлению два путешественника, первый позади второго. Проехав число дней, равное сумме чисел верст, проезжаемых ими в день, они съезжаются и узнают, что второй проехал 525 верст. Расстояние между городами – 175 верст. Сколько верст в день проезжает каждый?
Решение.
1) 175+525 = 700 (верст) проехал первый путешественник.
2) Пусть Х – число дней, которое проехал каждый путешественник. . Итак, 20 верст проехал первый путешественник, 15 верст проехал второй путешественник.
Задача № 2.
И.С. Тургенев «Муму»
«…Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рождения».
Решение.
Зная соотношения между старорусскими мерами длины и современными вычислим рост Герасима: 12* 4,5 см = 54 см. Рост младенца в среднем составляет 51-53 см. Какой же Герасим тогда богатырь? Но раньше указывали лишь число вершков, на которое он превышал два аршина. Проведем повторное вычисление:
1) 2*72см = 144см (2 аршина)
2)144 +54= 198см (2 аршина и 12 вершков).
Ответ: рост Герасима был 1м 98см - высокий человек.
Задача № 3.
Н. А. Некрасов « Дедушка Мазай и зайцы»
« Вижу один островок небольшой-
Зайцы на нем собралися гурьбой.
С каждой минутой вода подбиралась
К бедным зверькам; уж под ними осталось
Меньше аршина земли в ширину,
Меньше сажени в длину».
Каковы же размеры островка в современных единицах длины и площади?
Решение.
S= а*в, а = 1аршин=72см, в=1 сажень =216см. S= 0,72 *2,16 =1,5552 м2. Ответ: островок небольшой.
Задача № 4.
Л. Гераскина «В стране невыученных уроков»
Пять землекопов выкопали траншею в сто погонных метров за четыре дня. Сколько погонных метров выкопал каждый землекоп в течение двух дней при условии, что все землекопы выполнили одинаковый объем работ?
Решение.
1)100: 4: 5 · 2 = 10 (м)
Ответ: 10 м выкопал каждый землекоп в течение двух дней.
Задача № 5.
Григорий Остер «Задача про кактус»
Федя с одноклассниками и учительницей пошел на экскурсию в ботанический сад и там присел отдохнуть на кактус. 27 колючек он сумел вытащить из себя сам. 56 колючек достала из него учительница. Каждый из 24 его одноклассников вынул из Феди по 12 колючек. Оставшиеся 187 штук помогли добыть другие посетители ботанического сада. Узнай, сколько колючек торчало из кактуса до того, как Федя присел на него отдохнуть, если во время этого события кактус расстался с третьей частью колючек?
Решение:
3· (27+56+12· 24+187) = 1674 (кол.)
Ответ: 1674 колючки торчало из кактуса.
Задача № 6.
А. Аверченко «Экзаменационная задача»
«Два крестьянина вышли одновременно из пункта А в пункт Б, причем один из них делал в час четыре версты, а другой - пять. Спрашивается, на сколько один крестьянин придет раньше другого в пункт Б, если второй вышел позже первого на четверть часа, а от пункта А до пункта Б такое же расстояние в верстах, - сколько получится, если два виноторговца продали третьему такое количество бочек вина, которое дало первому прибыли сто двадцать рублей, второму восемьдесят, а всего бочка вина приносит прибыли сорок рублей».
Решение:
(120 + 80): 40 = 5 (бочек).
Следовательно, расстояние от пункта А до пункта Б равно 5 верстам.
Первый крестьянин пройдет это расстояние за 5: 4 - 1,25 (часа), а второй - за 4: 4 = 1 (час), т.е. затратит на этот путь на 0,25 часа меньше, чем первый. Поскольку второй крестьянин вышел на четверть часа позже второго, то они придут в пункт Б одновременно.
Задача № 7
Жюль Верн «Таинственный остров».
Герои Верна измеряли высоту скалы. Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены.
«- если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены. «0ба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее - 500 футам. По окончании измерений инженер составил следующую запись:
15:500 = 10:х,
500×10 = 5000,
5000:15 = 333,3.
«Значит, высота гранитной стены равнялась 333 футам».
Мне кажется, что Николай Николаевич Носов, помимо литературы увлекался математикой. Читая его произведения, я нашла три задачи
Задача № 1
Н. Н. Носов «Федина задача»
«На мельницу доставили четыреста пятьдесят мешков ржи, по восемьдесят килограмм в каждом. Рожь смололи, причем, из шести килограммов зерна вышло 5 килограммов муки. Сколько понадобилось машин для перевозки всей муки, если на каждой машине помещалось по три тонны муки?»
Решение:
1)450· 80 = 3600 (кг) – всего ржи доставили на мельницу.
2)3600: 6 = 600 (раз) – по 6 кг зерна имелось на мельнице.
3)5· 600 = 3000 (кг) – муки получилось после перемола зерна.
4)3000: 3000 = 1 (м) – понадобилась для перевозки всей муки.
Ответ: одна машина.
Задача № 2.
«Мальчик и девочка рвали в лесу орехи. Они сорвали всего 120 штук. Девочка сорвала в два раза меньше мальчика. Сколько орехов собрал каждый из них?»
Решение:
Пусть девочка сорвала х, а мальчик 2х.
Составим и решим уравнение:
х+2х=120.
Ответ: девочка собрала 40, а мальчик – 80 ор
Задача № 3
«В магазине было 8 пил, а топоров в три раза больше. Одной бригаде плотников продали половину топоров и три пилы за 84 рубля. Оставшиеся топоры и пилы продали другой бригаде плотников за 100 рублей. Сколько стоит один топор и одна пила?».
Решение:
Составим и решим систему уравнений.
Пусть топор стоит х руб., а пила стоит у руб.
12х + 3у=84 и 12х +5у=100.
Ответ: топор стоит 5 руб. и пила стоит 8 руб.
Как известно, Антон Павлович Чехов происходил из семьи торговца. Его отец Павел Егорович держал бакалейную лавку с весьма замысловатой вывеской «Чай, сахар, кофе, мыло, колбаса и другие колониальные товары». Дела шли плохо и, окончательно запутавшись в долгах, отец семейства покидает семью и скрывается в Москве. Вот тогда-то сын Антон, будучи гимназистом в Таганроге, был вынужден зарабатывать средства к жизни репетиторством. Отсюда, по всей вероятности, и возникла идея для будущего рассказа.
« Купец купил 138 аршин черного и синего сукна на 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.» ( напомним, что аршин – старая русская единица длины, аршин равен 71,12 см.)
Задача имеет несколько решений.
Рассмотрим их по порядку.
1. Семиклассник-репетитор готов был решать задачу "с иксом и игреком", будучи уверен, что задача - "собственно говоря, алгебраическая". И он, надо думать, легко справился бы с ней, прибегнув к помощи системы двух уравнений:
X + Y = 138
5X + 3Y = 540
2. Однако, задача легко решается и арифметически.
Если бы вам пришлось решать ее, вы начали бы с предположения, что все купленное сукно было синее. Тогда партия в 138 аршин стоила бы 5 * 138 = 690 рублей; это на 690 - 540 = 150 рублей больше того, что было заплачено в действительности. Разница в 150 рублей указывает, что в партии имелось более дешевое сукно по 3 рубля за аршин. Дешевого сукна было столько, что из двух-рублевой разницы на каждом аршине составилось 150 рублей: 150 / 2 = 75 аршин красного сукна и 138 - 75 = 63 - синего сукна.
3. В рассказе говорится очень кратко: "Он щелкает на счетах, и у него получается 75 и 63, что и нужно было". В чем однако состояло это "щелканье на счетах"? Каков способ решения задачи с помощью счетов?
Проследим же, какие действия должен был проделать на счетах Петин отец. Прежде всего ему нужно было, как мы знаем, умножить 138 на 5. Для этого он, по правилам действий на счетах, умножил сначала 138 на 10, - т.е. просто перенес 138 одним рядом выше, - а затем разделил это число пополам опять-таки на счетах же. Деление начинают снизу: откидывают половину косточек, отложенных на каждой проволоке; если число косточек на данной проволоке нечетное, то выходят из затруднения, "раздробляя" одну косточку этой проволоки на 10 нижних. В нашем случае делят 1380 пополам так: на нижней проволоке, где отложено 8 косточек, откидывают 4 косточки (4 десятка), на средней проволоке из 3 косточек откидывают 1 , а оставшуюся 1 косточку заменяют мысленно 10-ю нижними и делят пополам, добавляя 5 десятков к косточкам нижней; на верхней проволоке раздробляют одну косточку, прибавляя 5 сотен к косточкам средней проволоки. В результате на верхней проволоке совсем не остается косточек : на средней 1 + 5 = 6 сотен, на нижней 4 + 5 = 9 десятков. Итого 690 единиц. Далее Удодову-старшему нужно было из 690 вычесть 540. Наконец, полученную разность, 150, оставалось разделить пополам: Удодов откинул из 5 косточек (десятков) 2, отдав 5 единиц нижнему ряду косточек; потом из 1 косточки на проволоке сотен отдал 5 десятков нижнему ряду: получилось 7.
Задача № 2.
«Каникулярные работы институтки Наденьки Н.»
«Три купца внесли для одного торгового предприятия капитал, на который через год было получено 8000 рублей прибыли. Спрашивается: сколько получил каждый из них, если первый внес 35000 рублей, второй 50000 рублей и третий 70000 рублей?».
Решение:
1) 35000 + 50000 + 70000 = 155000 руб. – 100%
2) 155000: 100 = 1550 руб. – 1%
3) 8000: 1550 ≈ 5 %
4) 35000: 100* 5 = 1750 руб. – 1 купец
5) 50000: 100* 5 = 2500 руб. – 2 купец
6) 75000:100* 5 = 3750 руб. – 3 купец.
Ответ: 1750 руб., 2500 руб., 3750 руб.
Задачи Льва Николаевича Толстого
Как известно, великий русский писатель Л.Н. Толстой организовал в своем имении Ясная Поляна школу для крестьянских детей и сам преподавал в ней. Для учащихся он написал и издал «Азбуку», в которой есть раздел «Арифметика». Авторство первой задачи приписывают Льву Толстому, который придумал ее для учеников второго класса церковно-приходской школы.
Мне очень понравилось условие задач Л. Н. Толстого и я захотела проверить а справятся ли с решением этих задач современные школьники. Для этого мы провели исследования. Обучающимся 6, 8 и 10 классов нашей школы были предложены задачи, составленные Л.Н. Толстым.
Условие первой задачи:
Мужик продает шапку. За шапку хочет 10 рублей. Подходит покупатель, смотрит, меряет и решает купить. Дает 25 рублей одной купюрой. У продавца нет сдачи. Он посылает мальчишку- помощника к тете Клаве разменять деньги. Мальчишка деньги быстренько разменял и вернулся. Мужик отдал покупателю шапку, сдачу и тот ушел. Через некоторое время прибегает тетя Клава и заявляет, что деньги, которые принес на размен мальчишка фальшивые. Она предлагает мужику не ходить в участок, а прямо сразу вернуть ей деньги. Делать нечего, мужик лезет в карман и отдает тете Клаве свои кровные 25 рублей. Вопрос: На сколько денег «попал» продавец?
Решение.
Итак, мужик получил деньги только от тети Клавы, которая в результате размена вручила ему через мальчика 25 рублей. А выплачивал он деньги дважды — это сдача покупателю шапки(15 рублей) и возврат тете Клаве 25 рублей вместо фальшивых. В сумме — 40. Разница 40 – 25 = 15. Ответ: 15 рублей.
Условие второй задачи.
Трава на лугу растет одинаково густо и быстро. 70 коров могут поесть ее за 24 дня, а 30 коров – за 60 дней.
Вопрос: Сколько коров поели бы всю траву за 96 дней?
Решение.
Для решения возьмем вспомогательное неизвестное, которое будет означать суточный прирост травы в долях от ее запаса на лугу. В одни сутки произрастает У травы, в 24 дня – 24У, и если общий запас травы принять за 1, то всего коровы съедают 1+24У. В сутки все стадо (из 70 коров) съедает (1+24У):24, а одна корова съедает (1+24У):(24х70). Подобным же образом выведем количество травы для 30 коров в 60 суток: (1+60У):(60х30). Но количество травы, съедаемой коровой для обоих стад одинаково. Поэтому: (1+24У):(24х70) = (1+60У):(60х30), откуда У =  . Итак,
. Итак,  растет травы в одни сутки, 1 – запас травы был. Значит, за 96 дней травы станет: 1+96 *
растет травы в одни сутки, 1 – запас травы был. Значит, за 96 дней травы станет: 1+96 *  =
=  . одна корова съедает
. одна корова съедает  травы. 96 коров съедят
травы. 96 коров съедят  травы. Т.о.
травы. Т.о. 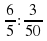 = 20(дней).
= 20(дней).
Ответ: 20 дней.
Условие третьей задачи.
Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели?
Решение.
Пусть было Х косцов, тогда они обкосили первый луг площадью: 4 * 8Х + 4 *4Х;
так как площадь второго луга больше в два раза, следовательно, его площадь 2 *(4*4Х + 1*8Х).
Составим и решим уравнение: 4 * 8х + 4 * 4х = 2 * ( 4 * 4х + 1 * 8х);
Х = 8.
Ответ: 8 косцов было в артели.
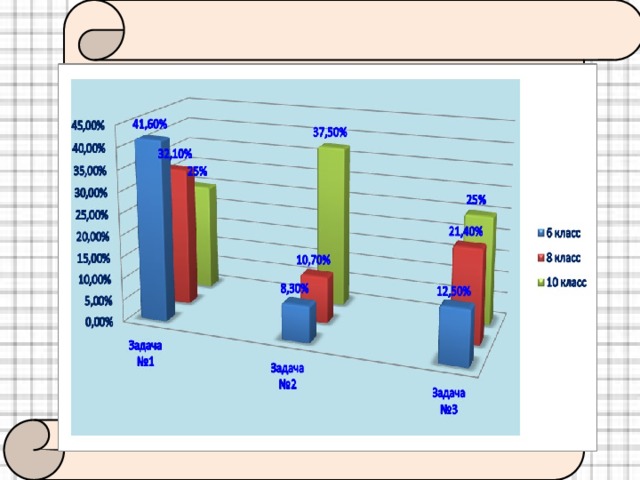
Были получены следующие результаты:
|
| 6 класс | 8 класс | 10 класс |
| Задача №1 | 41,6 % (10 человек) | 32,1 % (9 человек) | 25 % (4 человек)
|
| Задача №2 | 8,3 % (2 человека) | 10,7 % (3 человека) | 37,5 % (6 человек)
|
| Задача №3 | 12,5 % (3 человека) | 21,4 % (6 человек)
| 25 % (4 человека) |
![]()
Заключение
В ходе работы нами были сделаны следующие выводы:
— существует связь между математикой и литературой;
— математика обладает большим эстетическим потенциалом;
— был опровергнут стереотип о сухости математиков;
— найдены материалы, подтверждающие связь между литературой и математикой;
— использованы исторические сведения межпредметного характера;
— доказано присутствие математики в литературе.
Математика и литература не так далеки друг от друга, как многие думают. Искусство и наука требуют фантазии, творческой смелости, зоркости в наблюдении различных явлений жизни. Служение науке многие математики представляют себе неотрывным от служения литературе. Поэт должен видеть то, чего не видят другие, видеть глубже других. А это должен и математик.
В художественных произведениях можно заметить «руку математика». На страницах книг содержится много загадок, а иногда автор дает и отгадку.
Авторы, используя в своих произведениях математические данные, не просто дают готовые знания и выдают математические секреты, а предлагают читателю подумать и дают «пищу» для размышления. А разве книга не должна давать читателю пищу для ума?
Любая книга откроет свои тайны тому человеку, кто умеет смотреть и видеть, тому, кто умеет удивляться и воспринимать новое, тому, кто умеет сам добывать знания и отвечать на интересующие его вопросы.
Грамотное использование математических фактов делает художественное произведение достоверным и реальным.
Литература
1. Научно-теоретический методический журнал «Математика в школе», №3-2001. – 80с.
2. Научно-теоретический методический журнал «Математика в школе», №2-2005. – 80с.
3. Универсальная школьная энциклопедия. Т.З. Биографии/Глав. Ред. Е. Хлебалина; вед. ред. Д. Володихин. – М.: Аванта+, 2003. – 592 с.: ил.
4. Журнал «Математика» №17 – 1998.- 18с
5. Журнал «Математика» №9 – 1998.- 18с.
6. Л. Кассиль «Кондуит и Швамбрания» кн. 2, гл. « Задача с путешественниками».
7. Жюль Верн «Таинственный остров», гл. 14.
8. Л. Гераскина «В стране невыученных уроков.»
9. Н. А. Некрасов «Дедушка Мазай и зайцы.»
10. Н. Н. Носов «Витя Малеев в школе и дома.»
11. А.П. Чехов «Репетитор», «Урок арифметики».
12. Г. Остер «Задачник.»
13. И. С. Тургенев «Муму.»
15. Интернет – ресурсы:
1. http://dom.levent.ru/77.htm
2. http://chernov-trezin.narod.ru/Index.htm
3. http:/kurkino.net.ru/forumz/newreply.php?do=newreply&p=19249
4. Куликова Е., Куликова Е.В. «Математика и литература – два крыла одной культуры».
5. Латыпова С.В. «Математические задачи в литературных произведениях».
6. Митрофанова Н.В., Шохалова Н.П. «Мировоззрение и творчество А. С. Пушкина в свете математических законов».
Приложение
16
 «Над озером тихим,
«Над озером тихим, «Есть кадамба-цветок.
«Есть кадамба-цветок.
 «Путник! Здесь прах погребен Диофанта,
«Путник! Здесь прах погребен Диофанта, Из двух городов выезжают по одному направлению два путешественника, первый позади второго. Проехав число дней, равное сумме чисел верст, проезжаемых ими в день, они съезжаются и узнают, что второй проехал 525 верст. Расстояние между городами – 175 верст. Сколько верст в день проезжает каждый?
Из двух городов выезжают по одному направлению два путешественника, первый позади второго. Проехав число дней, равное сумме чисел верст, проезжаемых ими в день, они съезжаются и узнают, что второй проехал 525 верст. Расстояние между городами – 175 верст. Сколько верст в день проезжает каждый?  «…Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рождения».
«…Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рождения». « Вижу один островок небольшой-
« Вижу один островок небольшой-
 Федя с одноклассниками и учительницей пошел на экскурсию в ботанический сад и там присел отдохнуть на кактус. 27 колючек он сумел вытащить из себя сам. 56 колючек достала из него учительница. Каждый из 24 его одноклассников вынул из Феди по 12 колючек. Оставшиеся 187 штук помогли добыть другие посетители ботанического сада. Узнай, сколько колючек торчало из кактуса до того, как Федя присел на него отдохнуть, если во время этого события кактус расстался с третьей частью колючек?
Федя с одноклассниками и учительницей пошел на экскурсию в ботанический сад и там присел отдохнуть на кактус. 27 колючек он сумел вытащить из себя сам. 56 колючек достала из него учительница. Каждый из 24 его одноклассников вынул из Феди по 12 колючек. Оставшиеся 187 штук помогли добыть другие посетители ботанического сада. Узнай, сколько колючек торчало из кактуса до того, как Федя присел на него отдохнуть, если во время этого события кактус расстался с третьей частью колючек?  «Два крестьянина вышли одновременно из пункта А в пункт Б, причем один из них делал в час четыре версты, а другой - пять. Спрашивается, на сколько один крестьянин придет раньше другого в пункт Б, если второй вышел позже первого на четверть часа, а от пункта А до пункта Б такое же расстояние в верстах, - сколько получится, если два виноторговца продали третьему такое количество бочек вина, которое дало первому прибыли сто двадцать рублей, второму восемьдесят, а всего бочка вина приносит прибыли сорок рублей».
«Два крестьянина вышли одновременно из пункта А в пункт Б, причем один из них делал в час четыре версты, а другой - пять. Спрашивается, на сколько один крестьянин придет раньше другого в пункт Б, если второй вышел позже первого на четверть часа, а от пункта А до пункта Б такое же расстояние в верстах, - сколько получится, если два виноторговца продали третьему такое количество бочек вина, которое дало первому прибыли сто двадцать рублей, второму восемьдесят, а всего бочка вина приносит прибыли сорок рублей». Герои Верна измеряли высоту скалы. Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены.
Герои Верна измеряли высоту скалы. Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. 
 «Мальчик и девочка рвали в лесу орехи. Они сорвали всего 120 штук. Девочка сорвала в два раза меньше мальчика. Сколько орехов собрал каждый из них?»
«Мальчик и девочка рвали в лесу орехи. Они сорвали всего 120 штук. Девочка сорвала в два раза меньше мальчика. Сколько орехов собрал каждый из них?» «В магазине было 8 пил, а топоров в три раза больше. Одной бригаде плотников продали половину топоров и три пилы за 84 рубля. Оставшиеся топоры и пилы продали другой бригаде плотников за 100 рублей. Сколько стоит один топор и одна пила?».
«В магазине было 8 пил, а топоров в три раза больше. Одной бригаде плотников продали половину топоров и три пилы за 84 рубля. Оставшиеся топоры и пилы продали другой бригаде плотников за 100 рублей. Сколько стоит один топор и одна пила?». « Купец купил 138 аршин черного и синего сукна на 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.» ( напомним, что аршин – старая русская единица длины, аршин равен 71,12 см.)
« Купец купил 138 аршин черного и синего сукна на 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.» ( напомним, что аршин – старая русская единица длины, аршин равен 71,12 см.) Мужик продает шапку. За шапку хочет 10 рублей. Подходит покупатель, смотрит, меряет и решает купить. Дает 25 рублей одной купюрой. У продавца нет сдачи. Он посылает мальчишку- помощника к тете Клаве разменять деньги. Мальчишка деньги быстренько разменял и вернулся. Мужик отдал покупателю шапку, сдачу и тот ушел. Через некоторое время прибегает тетя Клава и заявляет, что деньги, которые принес на размен мальчишка фальшивые. Она предлагает мужику не ходить в участок, а прямо сразу вернуть ей деньги. Делать нечего, мужик лезет в карман и отдает тете Клаве свои кровные 25 рублей. Вопрос: На сколько денег «попал» продавец?
Мужик продает шапку. За шапку хочет 10 рублей. Подходит покупатель, смотрит, меряет и решает купить. Дает 25 рублей одной купюрой. У продавца нет сдачи. Он посылает мальчишку- помощника к тете Клаве разменять деньги. Мальчишка деньги быстренько разменял и вернулся. Мужик отдал покупателю шапку, сдачу и тот ушел. Через некоторое время прибегает тетя Клава и заявляет, что деньги, которые принес на размен мальчишка фальшивые. Она предлагает мужику не ходить в участок, а прямо сразу вернуть ей деньги. Делать нечего, мужик лезет в карман и отдает тете Клаве свои кровные 25 рублей. Вопрос: На сколько денег «попал» продавец?  Трава на лугу растет одинаково густо и быстро. 70 коров могут поесть ее за 24 дня, а 30 коров – за 60 дней.
Трава на лугу растет одинаково густо и быстро. 70 коров могут поесть ее за 24 дня, а 30 коров – за 60 дней. . Итак,
. Итак, 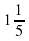 . одна корова съедает
. одна корова съедает  травы. 96 коров съедят
травы. 96 коров съедят 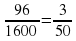 травы. Т.о.
травы. Т.о.  = 20(дней).
= 20(дней). Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели?
Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели?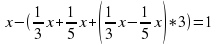
 . Итак,
. Итак,  . одна корова съедает
. одна корова съедает  травы. 96 коров съедят
травы. 96 коров съедят  травы. Т.о.
травы. Т.о. 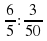 = 20(дней).
= 20(дней).