Унли касрларни таккослаш

ФАРХОД МЎМИНОВ

МАЛОХАТ ШОМИРЗАЕВА

МАТЕМАТИКАДАН ЁЗМА НАЗОРАТ ИШЛАРИ ВА МАСАЛА – ТОПШИРИҚЛАР

(ўқув қўлланма)

ТОШКЕНТ – 2009

ЎЗБЕКИСТОН РЕСПУБЛИКАСИ ХАЛҚ ТАЪЛИМИ ВАЗИРЛИГИ

ТОШКЕНТ ВИЛОЯТ ДАВЛАТ ПЕДАГОГИКА ИНСТИТУТИ

ФАРХОД МЎМИНОВ

МАЛОХАТ ШОМИРЗАЕВА

МАТЕМАТИКАДАН ЁЗМА НАЗОРАТ ИШЛАРИ ВА МАСАЛА – ТОПШИРИҚЛАР

ТОШКЕНТ – 2009

Бошланғич математика дарслигида ўқувчилар мавзулар бўйича ёзма назорат ишлари ҳамда тест бажарадилар. Ҳар бир назорат ишида нечтадан мисол – масала борлигини ҳам муаллимнинг ўзи тажрибаси асосида, синфнинг “кучи”га қараб хал қилаверади. Ушбу услубий қўлланмада назорат ишлари ва масала топшириқлар бўйича намуналар берилган.

Ўқув қўлланмадан “Педагогика” факултети бакалавр ва магистрлари,ҳамда бошланғич синф ўқитувчилари фойдаланишлари мумкин.

Масъул мухаррир:

Педагогика фанлари номзоди Г.Ниёзов

Тақризчилар:

Педагогика фанлари номзоди , доцент Даданов З.С.

Тошкент вилояти Ангрен шахар 20 – умумтаълим

мактабининг Бошланғич синф ўқитувчиси Йўлдошева У.

К И Р И Ш

Республикамиз мустақилликка эришгандан сўнг таълим сохасида катта ўзгаришлар амалга оширилмоқда. Жумладан Республика Давлат таълим стандартлари асосида мактаб дарсликлари амалиётга қўлланмоқда.

Дарсларни сифати ва самарадорли ўтишда назорат ишларининг ахамияти катта. Чунки назорат ишлари маълум бир тизим асосида ёзилади, бу эса ўқитувчи учун аниқ, равон дарс ўтиш йўлини белгилайди.

Ушбу услубий қўлланмани ёзишдан асосий мақсад, педагогика институтлари “Бошланғич таълим” йўналишида таълим олаётган талабалар ва ёш ўқитувчилар учун амалий ёрдам беришдир.

Услубий қўлланмада ёзма ишлар, тестлар, ҳамда ностандарт масала ва топшириқлар келтирилган.

Услубий қўлланмани ёзишда Республикамизнинг илғор педагогларнинг иш тажрибаларидан,ҳамда мақолаларидан фойдаланилади.

Услубий қўлланмадан олий ўқув юртларининг “Педагогика” факултети бакалаврлари ва магистрлари,ҳамда бошланғич синф ўқувчилари фойдаланишлари мумкин.

I – БОБ МАТЕМАТИКАДАН НАЗОРАТ ИШЛАРИ

1 § МАТЕМАТИКАДАН ЁЗМА НАЗОРАТ ИШЛАРИ

Қуйида услубий ёрдам сифатида назорат ишларининг намуналари берилади. Хар бир вариантга 1соат ажратилган. Ўқитувчи ўз вариантларини бироз осонлаштириб(ёки бироз мураккаблаштириб) тузиши мумкин.

4-синф «Математика» курсининг III-чорагида “Геометрия билан илк танишув”, “Касрлар хақида маълумотлар” ўрганилади. Ўқувчилар бу блокда (мавзулар мажмуаси) бўйича ёзма назорат иши бажарадилар. III-чоракда нечта ёзма назорат иши ўтказиш муаллимнинг иш режасида бор, албатта. Хар бир ёзма ишга нечтадан мисол-масала берилишини хам муаллимнинг ўз тажрибаси асосида, синфнинг “кучи”га қараб хал қилаверади. Фикримизча, III-чоракда 5та ёзма иш ўтказиш мақбул кўринади: 2таси ўтилган геометрик материаллар асосида, 2таси касрларга оид ва 1таси III-чоракда ўрганилган барча мавзулар бўйича якуний ёзма иш.

1-ЁЗМА НАЗОРАТ ИШИ.

1-вариант

1. Хисобланг:

1)2см.дм.+1м.2дм;

2)15см. 5мм.+4см.5мм.

1. Тўғри тўртбурчакнинг периметри 84смга, баландлиги эса 17смга тенг. Шу тўғри тўртбурчакнинг асосини топинг.

2. Учбурчакнинг периметри 48смга тенг.Унинг бир томони 12см, иккинчи томони 16см бўлса, учинчи томонини топинг.

3. Тўғри тўртбурчакнинг асоси 30см, баландлиги асосидан 10см қисқа. Шу тўғри тўртбурчакнинг периметрини топинг.

4. 1) 1дм² неча см²га тенг?

2) 1м² неча дм²га тенг?

Жавоблар:

1. 1) 3м 5дм; 2)20 см

2. 25см.

3. 20см

4. 1м

5. 1)100см²; 2) 10дм²

2-вариант

1. 1) 1м 4дм + 2м 3дм

2) 4дм 6см + 3дм 4см

2. Тўғри тўртбурчакнинг периметри 50см унинг бир томони 14см, иккинчи томони 20см. Учинчи томонини топинг.

3. Тўғри тўртбурчакнинг периметри 72 см .Асосининг узунлиги 22см. Баландлигини топинг.

4. Тўғри тўртбурчакнинг баландлиги 35 см. Асоси баландлигидан 10см узун. Шу тўғри тўртбурчакнинг периметрини топинг.

5. 1)185см² ни дм² ва см² ларда ифодаланг.

2)250дм² ни м² ва дм²ларда ифодаланг.

Жавоблар:

1. 1)3м7дм; 2)8дм

2. 14см

3. 16см

4. 1м 6дм

5. 1)1дм² 85см²; 2)2м² 50дм²

2-ЁЗМА НАЗОРАТ ИШИ

1-вариант

1.Учбурчакнинг томонлари 3 дм, 26см ва 24смга тенг. Унинг периметрини топинг. Натижани дмларда ифодаланг.

2.Тўғри тўртбурчакнинг баландлиги 15смга тенг. Асоси баландлигидан 9см узун. Шу тўғри тўртбурчакнинг юзини топинг.

3.Тўғри тўртбурчакнинг юзи 84дм², баландлиги 7 дмга тенг. Шу тўғри тўртбурчакнинг юзини топинг.

4.Квадратнинг периметри 12дм. Унинг юзини топинг. Натижани см²ларда ифодаланг.

5.1)1гектар неча м²га тенг?; 2)1сотих неча м²га тенг?

Жавоблар:

1. 8дм.

2. 360см².

3. 38дм.

4. 9дм²=900cм².

5. 1)10000м²; 2)100м².

2-вариант

1.Учбурчакнинг томонлари 22см, 3дм, 28смга тенг. Унинг периметрини топинг. Натижани дмларда ифодаланг.

2.Тўғри тўртбурчакнинг асоси 20 см, баландлиги асосидан 4см қисқа. Шу тўғри тўртбурчакнинг юзини топинг.

3.Тўғри тўртбурчакнинг юзи 96дм²га, асоси 16дмга тенг. Шу тўғри тўртбурчакнинг периметрини топинг.

4.Квадратнинг периметри 8дмга тенг. Унинг юзини топинг. Натижани см²ларда ифодаланг.

5.1)650м²ни ар ва м²ларда ифодаланг.; 2)10600м²ни гектар ва арда ифодаланг.

Жавоблар:

1. 8дм.

2. 320см²

3. 44дм

4. 4дм²=400см².

5. 1)6 ар 50м²; 2)1га 6 ар

3-ЁЗМА НАЗОРАТ ИШИ

1-вариант

1.Қайси каср катта:

1)7/8ми ёки 6/8ми? 2)4/7ми ёки 4/6ми? нима учун?

2.Хисобланг:

1)1/5+2/5; 2)7/9-5/9.

3. 1)1м нинг ярми неча см? 2)1т нинг ярми неча кг.

4.Хадича биринчи куни китобнинг 1/7 қисмини, иккинчи куни эса 2/7 қисмини ўқиди. Хадича икки кунда китобнинг қанча қисмини ўқиган?

5.Отабек баскетбол халқасига отилган 12та тўпдан 10тасини туширда.Халил эса 13та тўпдан 10 тасини туширди. Натижани каср кўринишида ёзинг. Кимнинг натижаси яхшироқ?

Жавоблар:

1.1)7/86/8,чунки 76; 2)4/7

2.1)3/5; 2)2/9.

3.1)50см; 2)500кг.

4.3/7 қисмини ўқиди.

5.10/1210/13.Отабекнинг натижаси яхши.

2-вариант

1.Қайси каср кичик:

1)5/9ми ёки 4/9ми? 2)5/8ми ёки 5/7ми? Нима учун?

2.Хисобланг:

1)5/7+1/7; 2)4/6-1/6.

3.1)1кгнинг ярми неча грамм?; 2)1соатнинг ярми неча минут?

4.Абдулхақ ота биринчи куни токзорнинг 1/5қисмига, иккинчи куни 2/5 қисмига ишлов бердилар. Ота икки кунда токзорнинг неча қисмига ишлов бердилар?

5.Ахмад II чоракда математикадан тест саволларининг 20тасидан 18тасига тўғри жавоб берди. III чоракда эса математикадан тест саволларининг 20тасидан 19 тасига тўғри жавоб берди. Унинг натижаларини каср кўринишида ёзинг. Ахмад қайси чоракда яхши натижага эришган?

Жавоблар:

1.1)4/9

2.1)6/7; 2)3/6.

3.1)500гр; 2)30минут.

4.3/5қисмга.

5.18/20 чоракдаги натижа яхши.

4-ЁЗМА НАЗОРАТ ИШИ

1-вариант

1.Камола ва Ахмад бингаликда топширилган ишнинг 5/8 қисминибажаришди. Ишнинг 3/8 қисмини Камола қилди. Ахмад ишнинг қандай қисмини бажарган?

2.Синфда 36 ўқувчи бор. Уларнинг 5/9 қисми қиз болалар. Синфда нечта ўғил бола бор?

3.1)1метрнинг 1/4 қисми неча см? 2)1тн нинг 2/5 қисми неча ц?

4.Валидаги ёнғоқларнинг 3/4 қисми 30та. Унда жами нечта ёнғоқ бор?

5.Йўлнинг 12км таъмирланди. Бу жами йўл узунлигининг 1/3 қисмига тенг. Йўлнинг жами узунлигини топинг.

Жавоблар:

1.2/8 қисмини.

2.16та.

3.1)25 см; 2)4 центнер.

4.40та.

5.36 км.

2-вариант

1.Топширилган ишнинг 2/9 қисмини, 3/9қисмини Хилола бажарди. Улар ишнинг қандай қисмини бажаришди.

2.Синфда 35та ўқувчи бор. Уларнинг 3/7қисми ўғил болалар.Синфда нечта қиз болалар бор.

3.1)1соатнинг 1/4қисми неча минут? 2)1тн нинг 3/10қисми неча центнер?

4.Наимадаги пулнинг 3/5қисми 300сўм. Наимада жами неча сўм бор?

5.Сайёх 15км йўл босди. Хисоблаб кўрса, ўтилган йўл жами йўлнинг 1/3 қисмига тенг экан?

Жавоблар:

1.5/9.

2.20та.

3.1) 15минут; 2) 3 центнер.

4.500сўм.

5.45 км

5-ЁЗМА НАЗОРАТ ИШИ

1-вариант

1.Тўғри тўртбурчакнинг периметри 70см га тенг. Асоси баландлигидан 5см узун. Шу тўғри тўртбурчакнинг юзини топинг.

2.Тўғри тўртбурчакнинг юзи 18дм², асоси эса 6дм га тенг. Периметрини топинг.

3.Турсуной томони 20см бўлган квадратнинг 3/8 қисмини яшил, 2/8 қисмини пушти рангга бўяди. Квадратнинг неча см2 юзи бўялмай қолди?

4.225кг нинг 5/9 қисми неча кг?

5.Қопдаги картошканинг ¾ қисми 45 кг га тенг. Қопда жами неча кг картошка бор?

Жавоблар:

1.300см 2

2.18дм.

3.150см2

4.125кг.

5.60кг.

2-вариант

1.Тўғри тўртбурчакнинг периметри 72см. Баландлиги асосидан 8 см қисқа. Шу тўғри тўртбурчакнинг юзини топинг.

2.Тўғри тўртбурчакнинг юзи 24 дм2, баландлиги эса 4дм га тенг.Периметрини топинг.

3.Шохида асоси 20см, баландлиги 15см бўлган тўғри тўртбурчакнинг 2/6 қисмини кўк,1/6 қисмини қизил рангга бўяди. Тўғри тўртбурчакнинг неча см2 юзи бўялмай қолди?

4.120 метрнинг 3/5 қисми неча метр бўлади?

5.Қопдаги гуручнинг 2/5 қисми 28кг. Қопда жами неча кг гуруч бор?

Жавоблар:

1.308см2

2.20дм.

3.150см2.

4.72м.

5.72кг.

2 § ДАРСЛИК БЎЙИЧА ТЕСТ САВОЛЛАРИ.

(3 – СИНФ УЧУН)

1.20+10+30нинг қийматинитопинг.

а)60; б)50; с)70.

2.7+7+7+7+7+7+7 нечага тенг?

а)7х6; б)7х7; с)7х1.

3.Қайси фигура квадрат бўла олади?

а ) б) с)

4.Пўлат 4ёшда , акаси 14 ёшкатта, акаси неча ёшда?

а)18ёшда; б)40ёшда; с)24ёшда.

5.Жавоби 50дан катта бўлган мисолни белгиланг.

а)6+17; б)45+12; с)90-50.

6.Қайси йиғинди тўғри тузилган?

а)72+27=99; б)36+54=80; с)13+77=93.

7.Қайси айирма тўғри хисобланган?

а) 80-47=47; б)55-36=11; с)70-25=45.

8.Тўғри хисобланган йиғиндини топинг...

а)74+19=84; б)18+47=65; с)28+17=46.

9.Масала тузинг ва ечинг.

Бор эди – 35метр

Қирқиб олинди – 8м ва 5м

Қолди - ?

а)22м; б)20м; с)43м.

10. Бир томони 6см бўлган квадратнинг периметри нечага тенг?

а) 18см; б)36см; с)24см.

11.7та алохида учбурчак тузиш учун нечта чўп керак?

а)21та; б)14та; с)49та.

12.Жавоби 32 бўлган мисолни топинг.

а)3*9+5; б)69-4*7; с)100-5*8.

13.Амаллар тартиби бўйича қайси амал биринчи бажарилади?

а)кўпайтириш ва бўлиш

б)кўпайтириш ва қўшиш

с)қўшиш ва айириш

14.Қайси тенглик ёки тенгсизлик тўғри қўйилган?

а)45:515; с)4*730.

15.Энг катта 2хонали сон неча?

а)22; б)98; с)99.

16.2кг неча грамм бўлади?

а)2000 г .; б)200 г.; с)1000 г.

3 § УЧ ХОНАЛИ СОНЛАРНИ РАҚАМЛАШ

1.800да нечта юзлик бор?

а)80та; б)8та; с)800та.

2.Ўтлоқда хаммаси бўлиб 80та қўй ва эчки ўтламоқда. Қўйлар 46та. Эчкилар нечта?

а)46та; б)40та; с)34та.

3.Томонлари 7см ва 4см бўлган тўғри тўртбурчакнинг периметирини топинг.

а)22см; б)14см; с)7см.

4.Қуйидагилардан иборат сонни айтинг: 7юзлик ва 5 ўнлик.

а)75; б)750; с)700.

Уч юздан битта кам сонни айтинг.

а)299; б)301; с)200.

6.24л сутни 3л. дан қилиб нечта банкага солиш мумкин?

а)5та; б)12та; с)8та.

7.64-8*5нечага тенг?

а)20; б)24; с)180.

8.348 сонида нечта юзлик, нечта ўнлик, нечта бирлик бор?

а)3та юзлик,4та ўнлик, 8та бирлик;

б)34та юзлик, 8та бирлик;

с)3та ўнлик 48та бирлик.

9.Қайсиқаторда ортиш тартиби тўғри кўрсатилган?

а)916,919,923,909,924,925.

б)708,710,712,714,716,720.

с)608,606,607,620,621,628.

10.Тўғри бажарилган ифодани белгиланг.

а)72:8+9*3=9+27+36

б)42-42:6=42-42=0

c)40-36:6=40-5+35

11.анинг ах740 тенгсизлик тўғри бўладиган қийматини топинг.

а)5; б)6; с)4.

12.Тенглик тўғри бўлиши учун қайси мисолда қавс тўғри қўйилган?

а)8*(18-14)=32

б)(8*18)-14=32

c)(8*18-14)=32

13.Агар v=42 бўлса v+12 ифодаси нечага тенг?

а)54; б)52; с)45.

14. 370сонида хаммаси бўлиб нечта ўнлик бор?

а)37та; б)7та; с)70та.

15.Сўмда ифодаланг.

а)800тийин =80 сўм; б)800тийин =800 сўм; с)800тийин =8сўм.

16.Қайси тенглик тўғри қўйилган?

а)6м 09см=69дм; б)4м 56см=456см; с)908тийин=9сўм.

17.Қайси тенглик тўғри?

а)3м=300см; б)9м=90см; с)4сўм=40тийин.

18.70-7*6нинг қийматини хисобланг.

а)38; б)28; с)48.

4 § НАЗОРАТ ИШЛАРИ

(I ярим йил учун)

2007-2008 ўқув йили учун мўлжалланган назорат ишларининг матнлари намунавий ва хар хил вариантларда бериляпти. Уларнинг хажми ва мазмуни бошланғич синф ўқувчиларининг ёш хусусиятларини хисобга олган холда тузилган.

Назорат ишларини ўтказишда ўқитувчи ўзининг режасидан келиб чиқиб дастурдан “олдин” ёки “орқада” қолганини хамда синфдаги ўқувчиларнинг ўзлаштиришини эътиборга олиши керак. Шунинг учун текширувчи назорат ишларини ўтказишдан олдин дастурнинг ўтилган мавзуларини аниқлайди ва топшириқларга тегишли ўзгаришлар киритади. Барча холларда методик жихатдан хам назорат ишларини ўтказиш талабларига объектив ўлчов сақлаш лозим.

1 – СИНФ

Ўқув йилининг биринчи ярмида ўқувчилар қуйидагиларни билиши лозим:

+/- а) 1,2,4 кўринишдаги қўшиш ва айиришга доир мисоллар ечиш. Қўшишга доир бир амалли мисоллар ечиш.

Шу билимларнинг шаклланишини текшириш учун ўқитувчи Н.Бикбаева, Э.Янгабоева муаллифлари томонидан тузилган “Математика дафтари” 1-қисмининг 32-бетидаги топшириқлардан фойдаланиш мумкин.

2 – СИНФ

Ўқув йилининг биринчи ярмида шқувчилар қуйидагиларни билишлари лозим:

100ичида сонларни ўқиш,ёзиш ва таққослаш; 100ичида санаш; икки хонали сонларни қўшилувчилар йиғиндисида кўрсата олиш; жадвалда қўшиш ва айиришнинг айрим холларини билиш;

40+30 , 40-30, 62+4, 4+62,

38+20, 79-40, 79-4, 38+2,

кўринишдаги мисолларни оғзаки хисоблаш; қўшишга, айиришга, таққослашга, сонни бир неча бирлик орттириш ёки камайтиришга доир масалалар ечиш.

Мазмунида қўшиш,айириш бўлган математик ифодаларнинг қийматини топишда терминларни ишлата олиш; кўрсатилган узунлик ёрдамида кесма чизиш.

2 – СИНФ

I – чорак

Оғзаки хисоб.

Математик диктант.

1.Сонларни камайиш тартиби бўйича 33 дан 19 гача ёзинг.

2.40 сони 80дан неча марта кам?

3.Биринчи қўшилувчи 40.Иккинчи 44га тенг. Йиғиндини топинг.

4.70ни 9та камайтиринг.

5.70ни 9та орттиринг.

6.камаювчи 65, айрилувчи 5. Айирмани топонг.

7.84 сонини хосил қилиш учун 9ни қайси сонга қўшиш керак?

8.6 сонини хосил қилиш учун қайси сондан 7ни айириш керак?

9.73 сони қайси сондан 7та ортиқ?

10.Камаювчи 20га тенг бўлган икки мисол тузиб ёзинг.

Ёзма ишлар

1 – ёзма иш

1 – қатор

1. Хисоблашларни бажаринг:

35+50 70+30

2+40 87-3

80-2 64-50

91-90 42+6

2.Масалани ечинг:

Столда 40та катак ва улардан 10та кам бир чизиқли дафтар бор. Столда нечта бир чизиқли дафтар бор?

3.Кўрсатилган сонларни битта орттириб ёзинг: 29, 58, 99.
4.Узунлиги 1дм 2смга тенг бўлган кесма чизинг.

5.Камаювчи айирилувчидан 8та ортиқ бўлган иккита мисол тузиб ёзинг.

6.Қуйидаги сонлардан фақат 68дан катта лекин 86дан кичик бўлган сонларни ёзинг: 68, 18, 75, 84, 35, 98.

2 – қатор

Хисоблашларни бажаринг:

42+20 90+10

4+70 57-4

80-6 53-40

99-90 64+6

2.Масалани ечинг.

Хорда 40та ўғил бола ва улардан 6та ортиқ қиз бола қатнашди. Хорда нечта қизлар қатнашди?

3.Кўрсатилган сонларни 1та камайтириб ёзинг: 60, 79, 50.

4.Узунлиги 1дм 1смга тенг бўлган кесма чизинг.

5.Айирувчи айирмадан 4та катта бўлган иккита мисол тузиб ёзинг.

6.Қуйидаги сонлардан фақат 57дан катта лекин 75дан кичик бўлган сонларни ёзинг: 9, 24, 57, 63, 71, 29.

Изох. Ушбу ва кейинги синфларда ўқувчиларнинг тайёргарлигини хисобга олиб ўқитувчи мазмуни мураккаброқ машқларни қўллаши мумкин (қўлламаслиги хам мумкин). Улар ўқувчиларнинг билимини бахолашга таъсир қилмайди. Фақат тайёргарлиги кучли бўлган ўқувчиларга яна хам билимининг мустахкам эканлигини исботлашга имконият яратади.

2 – ёзма иш

1 – қатор

1.Мисолларни кўчиринг ва ечинг.

68+30 85-80 74-4

66+4 57+40 100-5

2.Нуқталар ўрнига ,

9+4...85-80

4+7...15-8

17-9...6+7

16-7...16-6

3.Узунлиги 8см га тенг бўлган кесма чизинг.

2 – қатор

1.Мисолларни кўчиринг ва ечинг.

52+40 67-60 76-6

48+2 45+30 100-8

2.Нуқталар ўрнига ,

9+6...8+5

7+5...4+9

12-5...5+7

18-9...18-8

3.Узунлиги 6 см га тенг бўлган кесма чизинг.

3 – ёзма иш

1 – қатор

Масалани ечинг:

1.Саватда 13та, ликопчада эса ундан 4та кам нок бор эди. Ликопчада нечта нок бор?

2.Камол 6та, Рахим эса 11та ўйинчоқ ясади. Рахим нечта ортиқ ўйинчоқ ясади?

3.Ўқувчилар 7та дарахт кўчатини эккандан сўнг яна 9та қолди. Хаммаси бўлиб нечта дарахт кўчати экилди?

2 – қатор

Масалани ечинг:

1.Мохира 9та эртакни ўқиб бўлгандан сўнг яна 7таси қолди. Мохира хаммаси бўлиб нечта эртак ўқиши керак эди?

2.Товуқнинг 9та сариқ ва улардан 4та ортиқ қора жўжалари бор. Товуқнинг нечта қора жўжаси бор?

3.Эрталикда 12та қиз бола ва 8та ўғил бола иштирок этдилар. Эрталикда қиз болалар ўғил болалардан нечта кўп иштирок этдилар?

4.Лола мактабга Зухродан олдин лекин Ранодан кечроқ келди.Мактабга ким олдин келганини ёзинг.(ж: Рано)

II – чорак

1 – ёзма иш

Математик диктант

1 – қатор

Дафтарга фақат жавобларини ёзинг.

1.7+8 4+9 7+7 12-7

16-6 8+4 15-9 14-6

2.Болага 8та марка совға қилгандан сўнг маркалар сони 20та бўлди. Болада олдин нечта марка бўлган?

3.Донхўракда қушлар бор эди. Улардан 6таси учиб кетгандан сўнг 8таси қолди. Олдин донхўракда нечта қуш бўлган?

4.Пўлат 12 ёшда, синглисиэса 9ёш. Пўлат синглисидан неча ёш катта?

5.Эрталаб 19та сомса пишириб ёпилди. Улардан бир нечтаси ейилгандан сшнг 3таси қолди. Нечта сомса ейилган?

Изох: 2 – қаторни бажарувчи ўқувчилар ишлаганда 1 – қаторни бажарган ўқувчилар дафтарда 2 кесма чизадилар: бирининг узунлиги 4см, иккинчисиники ундан 3см узун.

2 – қатор

Дафтарга фақат жвобини ёзинг.

1.7+6 15-9 7+9 8+5

14-4 8+3 16-9 12-7

2.Ўқувчи 5та мисолни ечиб бўлган сўнг яна 12та мисол қолди. Ўқувчи хаммаси бўлиб нечта мисол ечиши керак бўлган?

3.Мунирага 4та дафтар совға қилгандан сўнг дафтарлари 11 та бўлди. Мунирада олдин нечта дафтар бўлган?

4.Кўп қаватли уйнинг баландлиги 20м, дарахтники эса 8м. Дарахт уйдан неча метр паст?

5.16та нон ёпиш керак эди. 7та нон ёпилди. Яна нечта нон ёпиш керак?

Изох: 1 – қаторни бажарувчи ўқувчилар ишлаганда 2 – қаторни бажарган ўқувчилар дафтарда 2 кесма чизадилар : биринчисининг узунлиги 2см, иккинчиси ундан 2см қисқа .

Ёзма ишлар

2 – ёзма иш

1.Мисолларни ечинг :

27+34 21-16 31-22

35+28 35-18 64+28

2.Таққосланг ва ,

12...6+5 16-9...8

7+9-19 5...13-8

3.Бўш катакларни тўлдиринг:

1м 8дм =…дм =...дм 56 дм =…м…дм

4.Қавсларни шундай қўйингки ,тенгликлар тўғри чиқсин:

40-6+2=32 20-9-9=2

3 –ёзма иш

1 – қатор

Масалаларни ечинг.

1.Бува 70 ёшда , невараси бувасидан 62 ёш кичик . Неварасининг ёши нечада ?

2. Қиз болалар мактаб ҳовлисида 18 метр , ўғил болалар эса 9 метр ортиқ йўл тозалашди .

Ўқувчилар ҳаммаси бўлиб неча метр йўл тозалашди ?

3.Таққосланг ва ,

30-5+18...30-(5+18)

2 – қатор

Масалаларни ечинг .

1.Невара 8 ёш , бувиси эса неварасидан 52 катта . Бувиси неча ёшда7

2ёБолалар боғчасига ўқитувчилар 15та қуёнча, ва улардан 9та ортиқ айиқчалар ясашди. Улар хаммаси бўлиб нечта қуёнча ясади?

3.Таққосланг ва ,

40-3+15...40-(3+15)

4 – ёзма иш

1 – қатор

Масалаларни ечинг.

1.Бир гурухда 37та, иккинчисида 4та бола бор. Қайси гурухда болалар кўп ва қанча кўп?

2.Узунлиги 71м га тенг бир ўрам арқондан олдин 8м, кейин 9м қирқиб олинди. Ўрамда неча метр арқон қолди?

3.Томони 3см га тенг бўлган квадрат чизинг.

2 – қатор

Масалаларни ечинг.

1.Югуриш мусобақасида 81 ўғил бола ва 73 қиз бола қатнашди. Мусобақага қатнашган болаларнинг қайси бири кўп ва қанча кўп?

2.Дўконга 42та велосипед келтиришди. Тушликгача 6та, тушликдан кейин 9та велосипед сотилди. Яна нечта велосипед сотиш керак?

3.Томонлари 4 см га тенг квадрат чизинг.

3 – СИНФ

1 – чорак

1 – ёзма иш

1 – қатор

1.Фақат жавобини ёзинг:

9*7= 4*3= 24:4= 36:6=

5*8= 7*3= 14:7= 35:5=

3*3= 8*6= 54:9= 72:8=

2*3= 2*2= 28:7= 18:9=

5*2= 2*5= 16:4= 48:8=

4*2= 5*3= 81:9= 27:3=

2.Амалларни бажаринг:

63+6 16+13 40-8 32-14

32+40 36-8 56-14 81-28

38+12 72-56 16+18 10+27

3. Таққосланг ва ,

706...760 300...299

823...832 899...900

4.Мактаб майдончасига 34қаторга лавлаги ва улардан 19 қатор ортиқ сабзи экилди. Хаммаси бўлиб қанча лавлаги ва сабзи экилди?

2 – қатор

1.Фақат жавобини ёзинг:

7*2= 8*4= 14:2= 10:5=

9*3= 5*9= 42:6= 16:8=

4*4= 7*6= 40:2= 63:9=

6*6= 8*5= 28:7= 21:7=

2*9= 9*9= 32:4= 72:9=

4*9= 2*9= 45:9= 18:6=

2.Амалларни бажаринг:

72+7 33+7 47-4 50-7

24+15 34+30 81-36 40-12

82-5 61-9 36+28 38+8

3. Таққосланг ва ,

240...204 599...600

653...635 700...699

4.Югуриш мусобақасида 3 – синф ўқувчиларидан 27та, сакраш мусобақасида 18та кам ўқувчи қатнашди. Мусобақада хаммаси бўлиб қанча ўқувчи қатнашди?

2 –ёзма иш

1 – қатор

1.Ўқувчилар биринчи қатордан 16, иккинчисидан 24 бошкарам узишди ва қуёнларга 8тасини беришди. Неча бош карам қолди?

2.Амалларни бажаринг:

17-9 56-27 17+9 56+27

36-18 61-39 36+18 61+39

3*.Кўпайтмаси 12га тенг бўлган хамма сонларнинг жуфтини ёзинг.

4*.20та ўқувчи ўтириши учун 8та икки ўринли парта етадими?

Изох.

3*.Жавоб: 1ва 12, 2ва6, 3ва4.

4*.Жавоб: 2*8=16, 16

2 – қатор

1.Саёхатчилар биринчи куни 12км иккинчи куни 18км масофани босиб ўтдилар. Яна 23км масофани босиб ўтишлари керак. Хаммаси бўлиб саёхатчилар неча км масофа босиб ўтишлари керак бўлган?

2.Амалларни бажаринг.

18+7 37+28 18-7 37-28

45+19 53+29 45-19 53-29

3*.Шундай бир сон ўйлаб топингки, у хам 3га, хам 4га, хам 6га бўлинсин.

4*.Уч ўртоқ шахмат ўйнамоқда. Хар бири 2та партиядан ўйнади.Хаммаси бўлиб неча партия ўйин ўйналди?

Изох:

3*.Бундай сонлар кўп. Ўқувчилар 12сонини ёзиб қўяверсинлар, чунки бу сон 3,4,6га бўлинади.Агар вақт қолса бошқа сонларни (масалан,28,48 ва х.к.) хам ёзишлари мумкин.

4*.Ўқувчилар хато қилишлари хам эхтимол: 2*3=6, чунки бу масалалар кўпайтириш йўли билан ечиладиган масалаларга ўхшайди. Тўғри жавоб: 6, чунки биринчи бола иккинчи ва учинчи бола билан ўйнаган бўлса, бу демак 2партия хисобланади, иккинчи бола учинчи бола билан ўйнади. Бу яна бир партия. Хаммаси бўлиб 3. Шунда хам бир бола 2тадан партия ўйнаган бўлади.

3 – ёзма иш

1 – қатор

1.Ёш табиатшунослар биринчи иссиқхонага 47 қатор бодринг экишди. Помидор эса 14 қатор ортиқ. Сабзи помидор ва бодринг неча қатор экилса, шунча. Ёш табиатшунослар неча қатор сабзи экишди?

2.Далада хаммаси бўлиб 38 киши ишлайди. Улардан 17таси аёллар, қолганлари эса эркаклар. Далада ишлаётган эркаклар ёки аёллар кўп қанчага кўп?

3.Ховлида 35та бола ўйнаяпти. Бир нечтаси кетгандан сўнг у ерда 19 бола қолди. Нечта бола кетган?

2 – қатор

1.Мактабни таъмирлаш учун 26 банка яшил, оқ бўёқ эса яшилдан 8та кам, жигарранг бўёқ яшил ва оқ бўёқ биргаликда қанча бўлса шунча бўёқ сотиб олинди. Мактабни таъмирлаш учун қанча жигарранг бўёқ олинди?

2.Шахарга 21 машина сабзавот юборилди, улардан 9тасига карам, қолганларига – картошка ортилган. Шахарга жўнатилган машаналардан қайси бири кўпроқ ва қанча кўп: картошка ортилганми ёки карам?

3.Велосипедчилар 17км йўл босиб ўтгандан сўнг яна 9км ўтишлари керак. Велосипедчилар хаммаси бўлиб неча км масофа босиб ўтишлари керак?

4 – ёзма иш

1 – қатор

1.Амалларни бажаринг:

28+36 57+35

1. 20-16

26+40 37+47

1. 80-39

2.Ифодаларни ёзинг ва қийматини хисобланг:

1)120сони 70дан қанча ортиқ?

2)620 ва 360 сонларининг йиғиндисини; 840 ва 530 сонларининг айирмасини топинг.

3)Камаювчи 970, айирилувчи 860.Айирмани топинг.

3.Тенгламани ёзинг ва уни ечинг:

400га қайси сон қўшилса 510 хосил бўлади?

4*.Столда 12та кубик бор. Уларни катта қутига 6тадан ва кичик қутига 3тадан жойлаштириш керак. Шу кубикларни жойлаштириш учун нечта ва қандай қутилар керак бўлади?

Изох

4*.Ўқувчилар хар қайси имкониятни топишлари керак: 2та катта ва 4та кичик; 1та катта ва 2та кичик қутилар. Ечилиш усуллари ўқувчиларнинг ўзларига хавола.

2 – қатор

1.Амалларни бажаринг:

56-18 80-28

72-36 47-35

37-28 63+19

64-59 24+30

2.Ифодаларни ёзинг ва қийматини хисобланг:

1)60сони 130дан қанча кичик?

2)740ва 520сонларининг айирмасини; 460 ва 310 сонларининг йиғиндисини топинг.

3)Биринчи қўшилувчи 750, иккинчиси 40. Йиғиндини топинг.

3.Тенгламани ёзинг ва уни ечинг:

қайси сондан 60 айирилса 140сони хосил бўлади?

4*.Доктор болага ичиш учун 3тадан дори –дармон 7кунга ёзиб берди. Онаси дорихонадан олган 50дона дори-дармон шу болага етарли бўладими,йўқми?

4*Ушбу масалани болалар қуйидагича ечишлари эхтимол. 3*7=21

Жавоб: 21 ёки 3*7=21, 50-21=29

Жавоб: 29

Бу жавобларнинг иккаласи хам нотўғри. Масалани болалар қуйидагича 3*7=21ечганларидан сўнг ; 50сони билан таққослашлари мақсадга мувофиқ бўлади 5021. Демак, масаланинг ечимини қуйидагича ёзилганини кўрсатиш лозим:

1. 3*7=21;

2. 5021. Жавоб етади.

2 – чорак

1 –ёзма иш

1 – қатор

1.Амалларни бажаринг:

45+79 632-453

186+418 307-156

225+694 416-237

347+125 900-354

2.Ифодаларнинг қийматини топинг:

1)(62+8):7+39 2)40-32:8:2

3.Сабзавот омборида хар бирига 3кг дан 20 халта картошка ва 2 кг дан 15халта сабзи бор. Хамма сабзавот қанча?

4*.6 ва 0 сонлари ёрдамида хамма уч хонали сонларни ёзинг,

5*.Ушбу шаклда хаммаси бўлиб нечта тўғри тўртбурчаклар бор?

Изох.

4*.Жавоб: 600,606,660,666.

5*.Жавоб: 18.

2 – қатор

1. Амалларни бажаринг:

37+78 580-127

156+249 428-165

461+344 836-258

278+356 700-278

2.Ифодаларнинг қийматини топинг.

1)30:(10-4)+4 2)35:7+3*4

3.Болага 20та катак дафтар, улардан 5марта кам расм дафтари,катак дафтарива расм дафтари қанча бўлса шунча бир чизиқли дафтар сотиб олишди. Болага нечта бир чизиқли дафтар сотиб олинди?

4*.Қуйидаги ифоданинг қийматини хисобланг: (18:3:3):(18:3:3)

5*.Синфимизнинг учинчи ўқувчиси математика тўгарагига қатнашади. Агар тўгаракда 12 киши бўлса, унда синфимизда нечта ўқувчи бор экан?

Изох:

4*.Ушбу ифоданинг қийматини хисоблашлари шарт эмас; ифоданинг қиймати 1га тенг эканлиги шундай кўриниб турибди. (икки бир хил соннинг бўлинмаси). Лекин айрим ўқувчилар ифодага қарамай унинг қийматини хисоблайдилар: 18:3=6, 6:3=2 ва х.к. Синфда шу ишни бажарганлар ўқувчилар сони аниқланса мақсадга мувофиқ бўлар эди.

5*.Ечилиши: 12*3=36 Жавоб: 36

2 –ёзма иш

1 – қатор

1.Амалларни бажаринг:

484+48 597-398

346+278 500-273

258+469 458-239

621+197 604-132

2.Ифодаларнинг қийматини топинг:

27:9+52 (80-35):9

8*4-14 (57-56)*8

3.Челакда 8 л, чойнакда эса ундан 4марта кам сув бор. 5та шундай чойнакданеча литр сув бор?

4*.Ака-укаларда баробар ёнғоқ бор. Акаси укасига 1тасини берди. Укасида акасиникига қараганда нечта кўп ёнғоқ бўлди?

Изох:

4*.Масала бир қарашда осонга ўхшайди. Айрим болалар бу масалани укасида 1та ёнғоққа кўп бўлди деб ечадилар. Лекин бу ундай эмас. Акаси укасига 1та ёнғоқ бергандан сўнг, укасида акасининг қолган ёнғоғидан 1та кўп бўлди,акасида эса 2та кам бўлди. Бу масаланинг ечилиши қуйидагича: масалан, ака-укаларда 7тадан ёнғоқ бор. У укасига 1 тасини берса,6та ёнғоқ қолади.7-1=6, укасида эса (6+2-8) (8-6=2). Қайси сон олинмаса, жавобида 2 чиқади.

2 – қатор

1.Амалларни бажаринг:

555+79 451-282

108+465 600-377

524+293 957-728

365+365 508-364

2.Ифодаларнинг қийматини хисобланг:

32:8*7 (39-38)*7

9*6-18 24: (83-79)

3.Бидонда 24 л, банкада эса 8марта кам сут бор. 3та шундай банкада неча литр сут бор.

4*.Узунлиги 12м га тенг бўлган арқон тенг 3қисмга қирқилди. Арқон неча жойдан қирқилди?

Изох:

4*.Ўқувчиларнинг бир қисми нарсани тенг бўлакка бўлиш хақидаги масалага ўхшаш ечадилар. (12:3=4). Бу нотўғри.

Масаланинг жавоби: 2 жойдан

3 –ёзма иш

1 – қатор

1.Йиғинди ва айирмани топинг:

437 ва 156 810 ва 95

169 ва 71 536 ва 464

2.Китоб 100 бетли. Рустам чоршанба куни 15 бет, пайшанба куни эса 3 бет кам ўқиди. Рустам яна неча бет ўқиши керак?

3*.Темурнинг фикрича , агар бир сон 2 ва 3га бўлинса, у ўзининг йиғиндисига хам бўлинади. Шу фикр тўғрими? нотўғрилигини исботланг ва мисол келтиринг.

4*.Узунлиги 15м га тенг бўлган йўлга икки томонидан 1 тадан терак экилди. Бир – биридан тенг масофада яна 2та терак экишди. Хар бир қўшни теракнинг орасида неча метр масофа бор?

Изох:

3*.Жавоб нотўғри.Масалан, 6 сони 3га ва 2га бўлинади. Лекин 6 сони 5га бўлинмайди.

4*.Жавоб: 5м.

2 – қатор

1.Йиғинди ва айирмани топинг.

405 ва 399 632 ва 188

193 ва 87 401 ва 296

2.Жавонга 8та уч литрли банкагаузум шарбати ва худди шундай банкада томат бор. Жавонда хаммаси бўлиб неча литр шарбат ва томат бор?

3*.Тарозининг чап томонидаги палласида тарвуз, ўнг томонидаги палласида қовун ва 1кг ли учта тош турибди. Тарвуз қовундан неча кг ортиқ?

4*.АВ ва ВС кесмаларнинг узунлиги биргаликда АС кесманинг узунлигига тенг. АС кесманинг узунлиги эса 16см.

A_______________________________B____________________C

АВ ва ВС кесмаларнинг орасидаги масофани топинг.

3*.Жавоб: 3кг га.

4*.Ечими: 16:2-8. Жавоб: 8см.

4 –ёзма иш

1 – қатор

1.Пароход биринчи суткада 145км, иккинчи суткада биринчисига қараганда 63км га ортиқ, учинчи суткада иккинчисига қараганда 80км га кам масофани босиб ўтди. Учинчи суткада пароход неча км масофани босиб ўтди?

2.Эрталаб дўконда 813 кг гуруч бор эди . Кундузи 508кг сотилди ва яна 280 кг келтирилди. Куннинг охирида дўконда неча кг гуруч бўлди?

3.Бир залда хар бирида 8тадан 7 қатор, иккинчисида хар бирида 9 тадан 9 қатор стул бор.Иккинчи залда биринчи залга қараганда стуллар қанча ортиқ?

2 – қатор

1.Биринчи бригада 450та, иккинчиси улардан 12та ортиқ, учинчиси эса иккинчисидан 132та кам ток кўчати экишди. Учинчи бригада қанча ток кўчати экишди?

2.Учта уйда 385та ахоли яшайди. Ахоли сони биринчисида 134, иккинчисида 47та. Учинчи уйда қанча ахоли яшайди?

3.Бир қутида 6 тадан 4қатор,иккинчисида 8тадан 4 қатор кубиклар бор. Иккинчи қаторда биринчисидан қанча ортиқ кубик бор?

4 – СИНФ

1 – чорак

1 – ёзма иш

Математик диктант.

1.Иккинчисинфнинг 3бирлигидан ва биринчи синфнинг 40та бирлигидан иборат сонни ёзинг. Шу сонни 10марта камайтиринг.

2.5-хонанинг 6та бирлиги ва 3-хонанинг 8та бирлигидан иборат сонни ёзинг. Шу сонни 10 марта орттиринг.

3.10000дан 7та кичик сонни ёзинг.

4.9400 ва 300 сонларнинг йиғиндисини топинг.

5.1800 сони 800дан қанча ортиқ.

6.300 сонини хосил қилиш учун қайси сонни 3га бўлиш керак?

7.3010сонини 40та орттиринг.

8.Ортиш тартибида қуйидаги сонларни ёзинг:30050, 53000, 5003, 3050, 5300, 50030.

9.Энг кичик икки хонали сонни 100марта орттиринг.

10.7, 70, 700 сонларини уч марта орттиринг.

11.12, 120, 1200 сонларини 6 марта камайтиринг.

Изох:

8, 10, 11топшириқлар доскада ёзилади.

2 –ёзма иш

1 – қатор

1.Дафтарга фақат жавобларини ёзинг:

80:16 9348-40

700*100 520000-10000

4599+1 4900:7

17000*2 603300-330

2.4998 дан 5003гача бўлган сонларни ёзинг.

3.Тенгликлар тўғри чиқиши учун “дарчалар”га қайси сонларни ёзиш керак?

8040-...=8000 5+82=5000+700+…+2 92000+…=92038

4. Таққосланг ва ,

63м 09см...36м 9дм 4800кг...4т 8ц 70мин... 1с 20мин

5. Тенгсизликлар тўғри чиқиши учун “дарчалар”га қайси сонларни ёзиш керак?

...549: (0, 1, 2, 3, 4, 5, 6, 7)

2 – қатор

Дафтарга фақат жавобларини ёзинг.

91:13 5356-50

300*1000 280000-100000

4899+1 4200:7

709900-9900 1400*4

2.4997 дан 4003гача бўлган сонларни ёзинг.

3. Тенгликлар тўғри чиқиши учун “дарчалар”га қайси сонларни ёзиш керак?

7030-...=7000 2938=2000+900+…+8 63000+…=63027

4. Таққосланг ва ,

27м 06см…72м 6дм 4500кг…4т 5ц 1с 10мин…80мин

5. Тенгсизликлар тўғри чиқиши учун “дарчалар”га қайси сонларни ёзиш керак?

7…34172341 Жавоб: (3, 4, 5, 6, 7, 8, 9)

3 – ёзма иш

1 – қатор

1.Масалани ечинг:

Кўргазмага 54та расм келтирилди. Катта залга 18та, 4та кичик залга қолган расмларни 3тадан баробар жойлаштиришди. Кичик залда нечта расм бор?

2.Амалларни бажаринг:

800-640:8 12*6

210+90*7 84:28

16*4 76:19

3.Икки кесма чизинг: бирининг узунлиги 9см, иккинчисиники 3марта қисқароқ.

2 – қатор

1.Масалани ечинг:

Китоб 30 бетдан иборат. Ўқувчи хар куни 3 бетдан 6 кун ўқиди. Яна неча бет ўқиши керак?

2.Амалларни бажаринг:

480-80*5 23*4

75-5+9*2 81:27

17*4 90:18

3.Икки кесма чизинг: бирининг узунлиги 8см, иккинчиси ундан 2марта узунроқ.

4 – ёзма иш

1 – қатор

Масалаларни ечинг:

1.Ўқувчилар 3та бир хил қатордан 18та дарахт кўчати экишди. Хар бир қаторда нечтадан дарахт бор?

2.Бир ўрамда 40м чит бор. Сотувчи 3та харидорга 6 метрдан чит сотди. Ўрамда неча метр чит қолди?

3.Ўқувчилар мактаб тажриба майдончасидан биринчи куни 38кг, иккинчи куни эса 16кг ортиқ сабзи йиғиб олишди. Икки кунда ўқувчилар неча кг сабзи теришди?

2 – қатор

Масалаларни ечинг:

1.3та ликобчада 15та олма бор. Битта ликобчада нечта олма бор?

2.Омборда 45кг печенье бор. Хар бирига 8кгдан 5та яшикка печенье жойлаштиришди. Жойлаштириш учун яна неча кг печенье қолди?

3.Ўқувчилар биринчи куни 26та, иккинчи куни эса 18та ортиқ китоб таъмирлашди. Икки кунда ўқувчилар хаммаси бўлиб нечта китоб таъмирлашди?

2 – чорак

1 – ёзма иш

Математик диктант

1.Хисобланг ва жавобларини ёзинг:

645-40 120*6

860-800 110*6

275-25 510:3

480+20 350:3 (Мисолларни доскага ёзиб қўйиш мумкин)

2.6та бола ўзаро 90та ёнғоқни баравардан бўлиб олишди. Хар бир болага нечтадан ёнғоқ тўғри келди?

3.Бир йилда туманда хар бирига 8та хонадондан 6та янги уй қуришди. Ахолилар нечта янги уйга эга бўлишди?

4.Ошқовоқнинг массаси 12кг, қовунники эса 8кг га енгил. Ошқовоқнинг массаси қовуннинг массасидан неча марта ортиқ?

5.Соғ одамнинг юраги 1 минутда 75 марта уради. Юрак икки минутда неча марта уради?

6.3та қути чойнинг массаси 150гр. Шундай 10та қути чойнинг массаси қанча?

7.6та бир хил арча ўйинчоғини ясаш учун 48та рангли қоғоз керак. 8та шундай ўйинчоқ учун нечта қоғоз керак?

2 – ёзма иш

1 – қатор

1.Хисоблашларни бажаринг ва текширинг:

9836+1648 5004*9

1. 4104:6

2.Ифодаларнинг қийматини хисобланг:

701-45*2+18 (300-50):2

3.Фақат жавобларини ёзинг:

400-188 99+76

560+199 675-298

4.Ёзилишлар тўғри чиқиши учун юлдузча ўрнига тегишли белги қўйинг:

а) (16*8)х6=86-38 б) 24*3

Жавоб:а) “ - ” белгиси; б) “ : ” белгиси

2 – қатор

Хисоблашни бажаринг ва текширинг:

4915+1763 3008*7

30010-984 7668:9

2.Ифодаларнинг қийматини хисобланг:

310-60*3+140 (200-60)*5 600-120:3

3.Фақат жавобларини ёзинг:

700-19 99+84

280+220 573-384

4.Ёзилишлар тўғри чиқиши учун юлдузча ўрнига тегишли белги қўйинг:

а) (12*6)х7=91-49 б) 24*336:9+3

Жавоб:а) “ - ” белгиси; б) “ : ” белгиси

3 – ёзма иш

1 – қатор

1.Натижани хисобланг ва текширинг:

80309-7845 5043+25589

2.Тенгламаларни ечинг:

х-359=408 17*x85

3.Тенгликлар тўғри чиқиши учун бўш катакларни тўлдиринг:

6ц 54кг =…кг 6т 054кг =…кг 80400м =…км…м 2с16мин =…мин.

4*.Бирини тагига бирини 3та кесмани шундай чизингки, юқоридагиси 1дм дан қисқароқ, лекин ўртанчасидан 3 см га узунроқ, пастдагисидан эса 2см қисқароқ бўлсин.

Жавоб: (кесмалар қуйидаги узунликда бўлишлари мумкин) 7, 4, 9(см);6, 3, 8(см).

Ўқувчида берилган жавоблардан биттаси чиқиши керак.

2 – қатор

1.Натижани хисобланг ва текширинг:

70108-9435 2069+38126

2.Тенгламаларни ечинг:

845-х=501 95:х-19

3.Тенгликлар тўғри чиқиши учун бўш катакларни тўлдиринг:

1с 42мин =…мин 8т 045кг=…кг 8ц 45кг=…кг 52800м=…км…м.

4*.Бирини тагига бирини 3та кесмани шундай чизингки, юқоридагиси 1дм дан қисқароқ, лекин ўртанчасидан 4 см узунроқ ва пастдагисидан 2см қисқароқ бўлсин.

Жавоб: (кесмалар қуйидаги узунликда бўлишлари мумкин) 7, 3, 9(см);6, 2, 8(см).

Ўқувчида берилган жавоблардан биттаси чиқиши керак.

Масалани ечинг:

1.Буваси 72, невараси эса 9ёшда. Буваси неварасидан неча марта катта?

2.Икки пиёда бир вақтда икки қишлоқдан чиқди ва 2 соатдан кейин учрашди. Биринчиси соатига 4км, иккинчиси 2км тезлик билан юрган. Қишлоқлар орасидаги масофани топинг?

3.Бир тажриба майдончасига 240ц, иккинчисидан 2 марта кам картошка йиғиб олинди.Хамма картошкани баробардан 6 қопга жойлаштиришди.Хар бир қопда неча кг картошка бор?

2 – қатор

Масалаларни ечинг:

1.Невараси 8ёш, буваси эса 64 ёшда. Невараси бувасидан неча ёш кичик?

2.Икки қишлоқ орасидаги масофа 36км. Агар икки пиёда бир вақтда йўлга чиқиб улардан бирининг тезлиги 4км, иккинчисиники соатига 5км бўлса, улар неча соатдан кейин учрашадилар?

3.Бир майдондан 120кг олма териб олинди, иккинчисидан 4марта ортиқ. Хамма олмаларни 30та бир хил қопга солишди. Хар бир қопдп неча кг олма бор?

5 – ёзма иш

1 – қатор

1.Масалани ечинг:

1.Бир майдончадан хар бирида 30кг дан 12 қоп, иккинчисидан хар бирида 40кг дан 8 қоп пиёз теришди. Иккала майдончадан хаммаси бўлиб неча кг пиёз териб олишди?

2.Хисобланг.

2904-485 8070*4

1315+809 24045:3

3.Бўйи 12см ва эни ундан 2марта кичик бўлган тўғритўртбурчакнинг периметрини топинг.

2 – қатор

1.Масалани ечинг.

Хўжаликдан тегирмонга хар бирида 24ц дан 5 машини ва хар бирида 23ц дан 4 машина буғдой юборилди. Тегирмонга хаммаси бўлиб неча центнер буғдой юборилди?

2.Хисобланг.

2068-909 4090*6

1108+867 27054:9

3.Эни 5см ва бўйи ундан 3 марта узунроқ бўлган тўғритўртбурчакнинг периметрини хисобланг.

5 § НОСТАНДАРТ МАСАЛА – ТОПШИРИҚЛАР

Масалалар ечиш жараёнида “стандарт” (қолипдаги) ва “ностандарт” ибораларини ишлатамиз. Бошланғич синф математика дарсликларидаги аксарият, кўпчилик масалалар стандарт ечим масалалардир. Яъни берилган масала қайсидир тур (тип) га тааллуқлибўлиб, унинг ўзига хос белгиларига кўра ечим йўли мавжуд. Масалан, сонга йиғиндини қўшишга ёки сондан йиғиндини айиришга доир масалаларнинг ечим йўллари аниқ қоида (хосса)га бўйсинади. Бундай масалаларнинг ечим усуллари турлича бўлган тақдирда хам масала турига қараб ечиш усуллари аниқ йўл-йўриқ(қоида)га кўра бажарилади.

Ностандарт ечим йўлига эга бўлган масала – топшириқларда эса бирор аниқ йўл-йўриқ асосида ечим изланмайди, балки масала мазмунидан келиб чиқиб, масаланинг “янги”, “оригинал” ечим йўли изланади. Унинг ностандартлиги хам шу ерда.

Бундай ўқув – топшириқларнинг афзаллиги шундаки, у ўқувчининг мантиқий тафаккурини ўстиради, мустақил фикр юритиш кўникмасини таркиб топтиради, математика фанига бўлган қизиқишини оширади, масала ечимини излаш жараёнидаги қийинчилик,машаққатларга бардош билан қараш туйғусини, мақсадга интилишлик, сабр матонатлик, топқирлик каби хислатларни тарбиялаш вазифасини бажаради.

Бошланғич синф математика дарсликларида 23та шундай мазмундаги (ностандарт ечим йўлига эга бўлган ) масалал – топшириқлар бор. Бу бутун бошланғич синф математика дарсликларидаги ўқув топшириқларнинг 0,05% ини ташкил этади.

Албатта, бошланғич синф ўқувчисини бундай масала – топшириқлар билан таништириб бориш, амалиётда учрайдиган “ностандарт” кўринишдаги топшириқларни бажара билишга ундайди. Ўқувчи мустақил фикрлаб, ўзининг ечим йўлини қўллаб масалани ечади, топган ечим вариантидан завқланади. Бу эса ўз навбатида бошланғич синф ўқувчисининг ижодий фаолиятининг ривож топишига катта ёрдам беради.

Ностандарт масалаларни маълум гуруҳларга ажратиб бўлмаганидек, ностандарт ечим йўлига эга бўлган топшириқларни хам таснифлаб бўлмайди. Шу сабабли ностандарт ечим йўлига эга бўлган топшириқлар намуналарини келтириш мумкин.

Ўқувчининг айрим геометрик шаклларини чизиши билан боғлиқ қуйидаги топшириқни қараймиз:

1 – топшириқ:

Қаламни дафтардан узмаган холда бир чизиқдан икки марта ўтмаслик шарти билан а)учбурчак; б)тўртбурчак; в)битта диагоналли тўртбурчак; г)икки диагоналли тўртбурчак; д)очиқ конверт кўринишидаги геометрик шаклларни чизинг.

Бу топшириқ таркибида 5та топшириқ бўлиб, улар маълум тизимини ташкил қилади, оддийдан мураккабга қараб топшириқлар келтирилган. 1-синф ўқувчисида чизғич ёрдамида маълум узунликдаги кесмаларни чизиш, учбурчак томонларининг чизғич ёрдамида ўлчаш каби кўникмалар таркиб топгач, ўқувчини дастлаб варақда (бир тўғри чизиқда ётмаган)3та (.)ни белгилашни (бу ишни ўқитувчи доскада бажариб кўрсатади), белгиланган нуқталарни чизғич билан кетма ғ кет туташтириб, учбурчак ясашни ўргатади. Ўқувчида учбурчак ясаш малакаси хосил бўлгач, энди ўқувчи чизғичсиз варақда 3та (.)ни белгилаши ва уларни кетма – кет кесмалар ёрдамида (қаламни варақдан узмасдан) туташтиришни ўрганади. Бу ерда ўқитувчини ўқувчидан учбурчак чизаётган пайтда қайси нуқтадан бошлашдан қатъий назар, шу уч нуқтадан ўтувчи учбурчак чизиш м умкинлигини айтиш жоиз. Текис қоғоз варағига учбурчакни чизишни билган (қаламни варақдан узмасдан) ўқувчи, варақда (дастлаб иложи борича катакли варақ олингани мақсадга мувофиқ) тўғри тўртбурчакни мустақил равишда чиза олади. Бу топшириқни бажаришда қийналган ўқувчига ўқитувчи топшириқни бажаришга доир кўрсатма бериши мумкин: “Варақда 4 та нуқтани шундай белгилангки, 2тадан нуқталар бир қаторда ва 2тадан нуқталар бир қаторга тўғри келсин. Бу нуқталардан бирига қалам қўйиб, қаламни дафтардан узмасдан иккинчи нуқтаси билан тўғри чизиқ бўйича туташтиринг хамда қўлни узмаган холда 4 нуқта билан хам туташтиринг”.

Ушбу топшириқ таркибидаги в), г), д), топшириқларини бажариш, ўқувчисидан анча билим, малака ва кўникмаларини талаб қилади. Дастлаб ўқитувчи тўғри тўртбурчак
“диагонали” тушунчасининг ошкор таърифи келтирилмайди. Тўғри тўртбурчакнинг 1 – ва 3 – учлари (ёки 2 – ва 4 – учлари туташтирувчи) тўғри чизиқ кесмаси шаклида ошкормас таъриф бериш мумкин. в) топшириқ – бирдиагоналли тўртбурчак (қаламни дафтардан узмаган холда хамда чизиқ устидан 2 марта ўтмаслик шарти билан) чизиш топшириғини 2 –синф ўқувчилари мустақил бажара олишади. Бу шаклни чизишнинг турли вариантлари борлигини ўқитувчи таъкидлаб ўтиши жоиздир. Чунки тўртбурчакнинг қайси учидан бошлаб қалам (хох тўртбурчак томони бўйича, хох диагонали бўйича) юритилса, албатта сўралган шаклни чизиб бўлади.

г)топшириқ – 2 – синф ўқувчилари учун муаммоли топшириқ бўлиб хисобланади. Чунки, ўқувчи хар қанча уринмасин, топшириқ шарти бўйича икки диагоналли тўртбурчак чиза олмайди. Бу топшириқ ечимли топшириқ эмас, яъни қаламни дафтардан узмаган холда бир чизиқдан 2марта ўтмасдан иккита диагоналли тўртбурчак чизиб бўлмайди. Бу ерда шу нарсани таъкидлаш жоизки, “Ечиб бўлмайдиган (ечимга эга бўлмаган) топшириқларни бошланғич синф ўқувчиларига бериш мумкинми?” деган саволга айрим методистлар “бериш мумкин эмас” дейишса, айримлари “бериш мумкин” деган фикрларни билдиришган. Тажриба шуни кўрсатадики , “Ечимга эга бўлмаган топшириқлар”ни мухокама қилиб, уни ечиб бўлмаслигини кўрсатиш бу топшириқни тўғри хал қилишнинг бир йўлидир.

Бошланғич синф ўқувчиси бундай мазмундаги ижодий топшириқларни бажариш натижасида уларда қисман изланувчанлик, топқирлик, хатони топа билиш, мустақил фикр юритиб хулоса чиқара олиш каби кўникмаларнинг шаклланишига ёрдам беради.

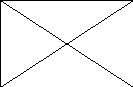
д)топшириқни бажаришда ўқитувчи 2 – синф ўқувчиларига “очиқ квадрат” шаклидаги геометрик шаклни кўрсатади. (1 - чизма). Шу шаклни ўқувчи дафтарида чизиши керак(шаклни чизиш шартига кўра). Шаклни турли вариантларда чизиш мумкин. Шу вариантлардан бирортасини ўқувчилар мустақил топшириқни бажаришгандан сўнг ўқитувчи тавсия қилиши мумкин. (Масалан, 2 – чизма)

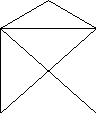
1 – чизма 2 - чизма

Бундай топшириқларни бажариш орқали ўқувчиларнинг геометрик шакл ва нақшларни тўғри ва аниқ чизиш кўникмалари таркиб топиш билан бирга уларнинг ақлий, ижодий фаолияти ривожланади.

2 – топшириқ

Қандай бир хил сонларнинг йиғиндиси шу сонларнинг кўпайтмасига тенг бўлади?

Иккинчи синф ўқувчиларига бериладиган бу топшириқ ечими икки вариантда бўлади:

2+2=2х2 0+0=0х0

Ностандарт ечим йўлига эга бўлган масала – топшириқларнинг бир кўриниши бу математик ребуслардир. Дарс жараёнида ўтказилган математик ребуслар ўқувчиларнинг математика фанига бўлган қизиқишини оширади, ўқувчи тафаккурини, мантиқий фикрлаш қобилиятини ривожлантиради. Бундай топшириқларни ўқувчилар иштиёқ билан бажаришади.

3 – топшириқ:

а)**** + 1=*****

Тўрт хонали сонга 1 ни қўшсак беш хонали сон хосил бўлади. Бу фақатгина 9999+1=10000 бўлганда бажарилади.

б)Фут+бол=ўйин

(765+324=1089)

Бундай топшириқлар нафақат ўқувчиларнинг хисоблаш малака ва кўникмаларини ривожлантиради, балки хисоблаш учун зарур мантиқий фикрлаш ва хисоблашдаги қонуниятни англаш кўникмасини таркиб топтириш учун хам хизмат қилади.

Стандарт ечим билан баъзи топшириқларни бажаришда ўқувчининг жуда кўп амалларни бажаришига тўғри келади. Ностандарт ечим йўли билан топшириқ тез бажарилиши мумкин.

4 – топшириқ:

Хисобланг:

а=100-9+98-97+...+4-3+2-1

Ушбу топшириқни бажаришда қуйидагича мухокама юритамиз:

100-99=1; 98-97=1; 96-95=1; ...; 4-3=1; 2-1=1;

Демак, жуфт сонлардан унга қўшни бўлган тоқ сонлар айириляпти. Хар бир айирма 1га тенг. Ифода қиймати 1х50=50 га тенг бўлади.

Кўпбурчак бурчакларини кесганда хосил бўладиган янги геометрик шаклдаги бурчакларни топишга доир топшириқлар хам ностандарт ечим йўлига эга бўлган топшириқлар жумласига киради. Шундай топшириқ намуналарини келтирамиз.

5 – топшириқ:

а)Учбурчакнинг бир бурчаги кесиб олинди (тўғри чизиқ бўйича). Хосил бўлган шаклда нечта бурчак қолди?

Ўқувчи кўпинча “кесиб олинди”, “қолди” каби сўзлар иштирок этган стандарт масалаларни еча туриб айириш амалини ишлатади. Аммо бу топшириқ ечимини топишда айириш амалидан эмас, балки қўшиш амалини қўллаб топшириқ жавобини топамиз. Учбурчак бир учи тўғри чизиқ бўйлаб кесилса, хосил бўлган шаклда тўртта бурчак бўлади.

б) “Квадрат учлари тўғри чизиқ бўйлаб кесилса, қандай шакл хосил бўлади?” деган топшириқ ўқувчидан мустақил фикр юритишни талаб қилади. Бу топшириққа ягона битта жавоб бериб бўлмайди. Чунки квадрат қандай кесилишига боғлиқ бўлади.

3 – чизма

1)Агар квадрат учлари бир хилда квадрат учидан бошлаб квадрат томонининг ярми тенг масофада кесилса, яна квадрат хосил бўлади(3 - чизма). Ушбу топшириқ иккинчи синфнинг охирги чорагида, “шаклнинг юзи” мавзуси билан танишгач берилса, мақсадга мувофиқ бўлади. Шу ерда ўқитувчи берилган топшириққа қўшимча қилиб қуйидаги топшириқни илова қилиши мумкин: “Ўқитувчи кесиб олинган квадрат учларидан қандай шакллар тузишингиз мумкин? Тузилган шакл юзи хақида қандай хулоса чиқара оласиз?”

Бу саволлар ўқувчи учун муаммоли бўлиб, бевосита амалий мазмундаги топшириқни бажаришларини тақозо этади. Хар бир ўқувчи якка тартибда ушбу топшириқни бажариб, 4та кесиб олинган квадрат учлари (тўғри бурчакли учбурчаклар)дан турли кўринишдаги геометрик шаклларни тузади. Бири тўғри тўртбурчак (4 - чизма) тузса, яна бири квадрат (5 - чизма), бошқаси эса параллеллограмм (6 - чизма) каби шакл ва нақшларни ясайдилар:

4 – чизма

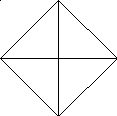5 – чизма 6 – чизма

Ўқувчилар тузган шаклларни кўздан кечирган ўқитувчи 5 – чизма яъни, тўртта учбурчакдан тузилган квадратга барча ўқувчилар диққатини жалб қилиб, бу учбурчаклар ёрдамида тузилган квадрат билан квадратдан қирқиб олингандан кейин қолган квадрат юзини таққослашни сўрайди. Ўқувчилар уларни устма – уст жойлаштириб, тенг юзали эканлигини пайқашади.

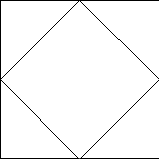
2)Агар квадрат учлари бир хилда квадрат учидан бошланиб, квадрат томонининг ярмидан камроқ масофада кесилса, 8 бурчакли геометрик шакл хосил бўлади(7 – чизма).

7 – чизма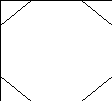

Шу ерда ўқитувчи квадратни дастлаб бир марта энига қараб, сўнгра хосил бўлган тўртбурчакни бўйига қараб буклаб, яна квадрат хосил бўлгач, квадрат (4та устма уст жойлашган)нинг очиқ бурчагидан квадрат томони ўртасига тенг масофага тўғри чизиқ бўйлаб кесилса, мунтазам 8бурчак хосил бўлишини ўқувчиларга амалий тарзда кўрсатиши ўқувчининг геометрик шаклларни маълум бўлакларга бўлиш ва турли геометрик нақшлар тузиш кўникмасини таркиб топтириш билан бирга, унинг чизиш, буклаш, қирқиш каби мехнат таълимига оид малака ва кўникмаларини оширади. Квадрат учларини турли тарзда тўғри чизиқ бўйлаб кесиш натижасида турлича геометрик шакллар хосил бўлишини амалий тарзда кўриб чиқиш мумкин бўлади.

6 – топшириқ:

Акмал кўп қаватли уйда яшовчи амакисининг уйига мехмонга борди. Амакиси 4 – қаватда яшайди. Иккинчи қаватга кўтарилгунча 24та зинани санади. Агар хар бир қаватдаги зиналар сони тенг бўлса, у нечта зинани босиб ўтди?

Ушбу топшириқ ечимининг ностандартлиги шу ердаки, ўқувчи биринчи қаватдан кўтарилаётган Акмалнинг 4 – қаватгача 24 тадан 3 марта (4марта эмас!) босиб ўтганини билиши керак. Жавоб: 24*3=72(зина)

7 – топшириқ:

Усталар 350м масофани телефон симёғочларини ўрнатиш топшириғини олишди. Хар 50м масофада битта симёғочи ўрнатилади. Агар хар бир симёғочни ўрнатиш учун 45минут вақт сарфланса, усталар бу ишни қанча вақтда бажарадилар?

Ушбу топшириқни бажаришган айрим ўқувчилар 350 : 50=7(та) симёғоч, 45*7=315(минут)вақт сарфланди деб айтадилар. Бу топшириқнинг ностандарт ечим йўлига эга эканлиги шундаки, 350м масофада хар 50м га биттадан симёғоч ўрнатиладиган бўлса, 8та симёғоч керак бўлади. Демак, масала ечими: 45*8=360(минут) = 6соат вақт керак бўлади.

8 – топшириқ:

Ўнликдаги рақами бирликдаги рақамидан катта бўлган барча икки хонали сонларни ёзинг.

Ушбу топшириқни 3 – синф ўқувчиларига бериш мумкин. Бу топшириқ ўқувчиларда қизиқиш уйғотади, чунки топшириқ ечими кўп қийматли. Ўқитувчи ўқувчилардан энг кичик икки хонали сон ва энг катта икки хонали сонларни ёзишни талаб қилади. Ўқувчилардан бирортаси доскага чиқиб энг кичик икки хонали сон 10, энг катта икки хонали сон 99ни ёзади. Шундан сўнг ўқитувчи ўқувчиларга қўшимча савол бериб: “Энг катта икки хонали сон 99 экан, ундан олдинги сон неча?” (98). Ўнлик хонадаги ва бирлик хонадаги рақамларни таққосланг (98). Бу сон берилган топшириқ шартини бажарадими? (ха). Энди топшириқни бажаринг. Ўқувчилар мустақил фикр юритиб, тузиладиган икки хонали сонда ўнликлар хонасида 9 рақами турса, бирликдаги барча рақамлар (9дан ташқари) 9дан кичик. Демак, 9 ва қолган рақамлардан фойдаланиб сонлар тузамиз: 98; 97; 96; 95; 94; 93; 92; 91; 90.

Ўнликлар хонасидаги 9 рақами билан сонлар тузилгач,энди икки хонали соннинг ўнлик рақами сифатида 8 танланади ва бирлик рақамлар 8дан кичик бўлган сонлар танланиб, сонлар тузилади: 87; 86; 85; 84; 83; 82; 81; 80.

Ўқувчилар бундай сонни қонуниятини ўргангач, синф ўқувчиларини гурухларга бўлиб, бир гурух ўқувчилар билан ўнлик хонадаги рақам 7 билан, иккинчи гурух ўқувчиларини ўнлик рақами 6 билан, учинчи гурух ўқувчиларини ўнлик рақами 5 билан юқоридаги шартни қаноатлантирувчи сонлар тузадилар. Масалан:

76; 75; 74; 73; 72; 71; 70.

65; 64; 63; 62; 61; 60.

54; 53; 52; 51; 50.

Бу ерда алохида шуни таъкидлаш жоизки, 3-синф ўқувчиси ушбу мисолни ечаётиб энг асосий сонлар қаторини хосил қилиш қонуниятини билиб олади ва тегишли хулоса чиқаришга интилади.

Шундан сўнг ўқитувчи “Юқоридаги шартни қаноатлантирувчи икки хонали сонлар нечта?” деган савол билан ўқувчиларга мурожаат қилади. Ўқувчилар бу саволга дархол жавоб беришлари мушкул. Шундан сўнг ўқитувчи қўшимча саволлар беради:

• Ўнлик хонадаги рақами тўққиз бўлган бундай икки хонали сонлар нечта? (9та)

• Ўнлик хонадаги рақами саккиз бўлган бундай икки хонали сонлар нечта? (8та)

• Ўнлик хонадаги рақами етти бўлган бундай икки хонали сонлар нечта? (7та) ва хоказо.Ўқитувчи ўқувчиларнинг тегишли хулоса чиқаришларини сўрайди ва қуйидаги саволни беради.

• Ўнлик хонадаги рақами 1 бўлган бундай икки хонали сонлар нечта? (1та)

Шунда 9дан 1гача бўлган сонлар йиғиндисини топиш масаласига келиб қолишади. Ўқувчилар 9 ва 8нинг йиғиндисига 7ни қўшиб топишлари керак. Шунда ўқитувчи 9 дан 1 гача бўлган сонларни қўшишнинг қулай усулини сўраса, ўқувчилар орасидаги 9га 1ни, 8га 2ни, 7га 3ни, 6га 4ни қўшиб, хар бир жуфтлик йиғиндиси 10 бўлишини ва бундай 10дан 4та борлигини, яъни 10*4 ва бу кўпайтмага 5ни қўшиш кераклигини айтадиган ўқувчилар чиқиб қолади. Демак, бундай икки хонали сонлар 10*4+5= 45 экан.

Шундай қилиб, бошланғич синф ўқувчиларини ностандарт ечим йўлига эга бўлган масала топшириқларни ечишга ўргатиш орқали уларда мантиқий тафаккур қилиш, мустақил фикр юритиш кўникмаси таркиб топади, масала – топшириқ шартига қараб ечимини излаш бўйича қисман тадқиқотлик, ўқувчини тпқирлик, изланувчанлик, мақсад сари интилувчанлик хислатларининг тарбияланишига олиб келади.

Мураккаб масала – топшириқлар

Маълумотлари етишмайдиган масалаларни ечишга ўргатиш орқали мантиқий тафаккур, сезгирлик, чидамлилик, топқирлик, мақсад сари интилувчанлик каби хислатлар тарбияланишига имкон яратади.

Маълумотлари етишмайдиган масала топшириқлар устида ишлашни тизимли равишда олиб бориш натижасида ўқитувчи бир томондан ўқувчиларнинг билим, кўникмаларини мустахкамлашни назарда тутса, иккинчи томондан ўқувчининг ақлий, ижодий фаолиятини ривожлантиришга эътиборини қаратади. Арифметик амал қонуниятлари ва хоссаларини ўрганар экан, ўқувчиларнинг шу амал хоссалари (сонга йиғиндини қўшиш, йиғиндини сонга қўшиши, сондан йиғиндини айириш, йиғиндидан сонни айириш, сонни йиғиндига кўпайтиришва шу кабилар)ни мустахкамлаш мақсадида турли хил мисол ва масалалар бажарилади. Шундай ўқув топшириқлари қаторида ўқувчиларнинг арифметик амал хоссаларини мустахкамлашни назарда тутиб маълумотлари етишмайдиган масала топшириқларни хам қараб ўқувчи ўқув-билув фаолиятини тфаоллаштиришга хизмат қилади.

Ўқувчилар йиғиндини сонга қўшиш((+)+)га доир маълумотлари етишмайдиган масала-топшириқларни бажаришни ўрганишлари ахамиятлидир. Дастлаб йиғиндидаги сон маълумотлар маълум бўлиб, қўшилаётган сон маълумот яширинган(берилмаган) холларда масала-топшириқларни бажариш мақсадга мувофиқ. Бундай топшириқлар шартида “Бўш катакча ўрнига сон маълумотни тўғри танлаб қўйинг ва масалани ечинг!” га ўхшаш фикр айтилиб, масала матни келтирилади: “Қафасда 8та кулранг ва 4та қора қуён бор. Анвар бозордан яна ...та оқ қуён олиб келиб қафасга қўйди. Қафасда нечта қуён бўлди? ”.

Ушбу топшириқни бажаришда ўқувчи ўзи мустақил сон маълумотни танлаб, катакчага қўйиб, “тўла матнли” масалани хосил қилади ва бу масалани мухокама қилиб ечади. Кейинчалик юқоридаги масала кўринишида қўшувчи сон маълумот умуман берилмаган тарзда келтирилади. Масалан, “Қафасда 8та кулранг ва 4та қора қуён бор. Анвар бозордан бир неча оқ қуён олиб қафасга қўйди. Қафасда нечта қуён бўзлди?”. Бу масалада етмсовчи сон маълумот “бир нечта” сўз орқали ифодаланган. Ўқувчи шу маълумотни ўзи танлаб, масалани “тўла матнли” масалага келтириб ечади.

Йиғиндига сонни қўшишга доир маълумотлари етишмовчи масалаларни қараб чиқишни давом эттириб, йиғиндидаги бирор қўшилувчи берилмаган холдаги ёки иккала қўшилувчи сон маълумотлари берилмаган холдаги масала топшириқларни хам қараш ўқувчининг ушбу мавзу юзасидан билим, кўникма ва малакаларини мустахкамлаши билан бирга, унинг ижодий фаоллигини оширади, креативлик (яратувчанлик) хислатлари шаклланишига ёрдам беради. Шундай масалалардан яна бирини келтирамиз.

Келтирилаётган масалада етишмовчи сон маълумотларини танлаб қўйиб, масалани ечинг. “Гулдонда атиргул ва чиннигул бор. Нодира бу гулдонга 4 та лола гулни қўяди. Гулдондаги гуллар нечта бўлди?”

Ўқувчи учун шартида маълумотлари етишмайдиган содда масалалар устида ишлаш юзасидан маълум тизимдаги кўникмалар шаклланганлиги туфайли бу масалани ўқигач, “Масалада гулдондаги атиргул ва чиннигуллар сон маълумотлари берилмаган” деган хулосага келишади. Улар сон маълумотларни мустақил танлаб, “тўла матнли” масалани хосил қилишади ва уни ечадилар. Бундай масалалар устида ишлашнинг яхши томони шундаки, масала шартида етишмовчи сон маълумотларни ўқувчи мустақил танлар экан, ўқувчининг якка тартибдаги фаолияти билан ўқувчилар умумсинф ўқув фаолият ўртасида мутаносиблик холати вужудга келади. Хар бир ўқувчи турли сон маълумотларни ишлатиб, масала матнини тўлдиради. Шунда синф ўқувчилари орасида танлаган сон маълумотлар қанчалик хақиқатга яқин ва тўғри танланганлиги аниқланади. Бу ўқувчиларни хамжихатликда фаолият кўрсатишга ундайди.

Маълумотлари етишмайдиган масала-топшириқлар худди йиғиндига сонни қўшиш хоссасига оид танланганидек, сонга йиғиндини қўшиш (+ (+)) , сондан йиғиндини айириш (- (+)), йиғиндидан сонни айириш (+)-), сонни йиғиндига кўпайтириш(* (+)), йиғиндини сонга кўпайтириш (+)*), йиғиндини сонга бўлиш(+):) каби қатор амал хоссаларига олиб масала – топшириқлар қараб чиқилиши мумкин. Бундай иш,бир томондан, ўқувчининг амал хоссаларига оид билим, малакаларини мустахкамлашга, иккинчидан, мустақил фикр юритиш кўникмасини таркиб топтиришга хизмат қилади.

6 § ОРТИҚЧА МАЪЛУМОТГА ЭГА БЎЛГАН МАСАЛА-ТОПШИРИҚЛАР.

Бундай ўқув топшириқларни бажаришдан мақсад ўқувчининг мантиқий тафаккурини ўстириш, масала матнидаги берилганлар ва изланадиган миқдорлар орасидаги боғланишни тўғри англай олишга ўогатиш билан бирга матндаги ортиқча маълумотларни аниқлаб, тўғри хулоса чиқара билишга ўргатишдан иборат. Ортиқча маълумотга эга бўлган масалалар билан ўқувчилар 1-синфда арифметик амаллар (қўшиш ва айириш) мазмунини очиб берувчи йиғиндини ва қолдиқни топишга доир масалаларни ўрганганларидан кейин таништириш мақсадга мувофиқ. Ўқувчи йиғиндини топишга доир масалалар устида ишлашни яхши ўрганганидан кейин унда қуйидаги мазмунда шартида ортиқча маълумот қатнашган масалаларни тавсия қилиш мумкин.

Масалаларни ўқинг, ортиқча маълумотларни аниқланг. Уларни ечинг.

1)Ўрдак 2кг, ғоз 3кг, товуқ 1кг. Ўрдак ва товуқ неча кг?

2)Собир, Нодир, Бобир балиқ овлашга чиқишджи. Собир – 9та, Нодир - 5та, Бобир – 6та балиқ тутишди. Нодир ва Собир нечта балиқ тутишди?

3)Дам олиш куни Лола ва унинг синглиси Нодира пахта йиғим – теримида ойисига ёрдам беришди. Нодира 10кг, Лола эса 15кг, ойиси 40кг пахта теришди. Нодира ва Лола неча кг пахта теришди?

Ўқувчилар бу масалаларни мухокама қилиб, биринчи масалада ғознинг массаси 3кг, иккинчи масалада Бобир тутган балиқлар сони 6кг, учинчи масалада болаларнинг ойисига терган пахтаси 25кг ортиқча маълумотлар эканлигинибилиб оладилар. Ўқувчи бундай ортиқча маълумотли масалаларни қизиқиш билан бажаради. Чунки бундай масалалар ўқувчидан тўғри фикр-мулохаза юритиш, шартидаги сон маълумотларни масала саволи билан таққослаб, қандай сон маълумотлар ортиқчалигини билиб олишга кўмаклашади. Бундай масалалар билан ишлашнинг яна бир афзаллик томони, ўқувчининг ижодий фаоллиги ошади. Ўқитувчи ўқувчилар билан ортиқча маълумотли масалалар устида ишлар экан, ўқувчи эътиборини фақатгина ортиқча сон маълумотни аниқлаб, масала ечимини топишга қаратмасдан, балки ортиқча сон маълумотдан фойдаланиб, “яна нималарни аниқлаш мумкин?” деган саволга жавоб топишга ўргатиб бормоғи шарт. Юқоридаги иккинчи масалада ўқитувчи ўқувчи билан бирга ортиқча маълумот (Бобир тутган балиқлар сони – 6та)ни аниқлаш билан бирга яна қуйидаги қўшимча саволларни ўқувчилар мухокамасига ташлаши ушбу масала ижодий изланишни талаб қилади.

-Ўқувчилар, масаладаги берилганларга қараб яна нималарни билиб олишингиз мумкин?(Нодир ва Бобирнинг тутган балиқлар сонини, Бобир ва Собир тутган балиқлар сонини). Хатто шундай ўқувчилар топиладики, “Нодир ва Собирнинг биргаликда қанча балиқ тутганини билиш мумкин?” деб хулоса чиқаришади. Шуни алохида таъкидлаш жоизки, бундай масалалар ўқувчиларни икки амалли масалалар билан таништиришга замин тайёрлайди. Дархақиқат, хали икки амалли масала билан таниш бўлмаган ўқувчи масала шартида ортиқча маълумоти бўлган учта сон маълумотга қараб, ўқувчининг берган “яна нималарни билиб олишингиз мумкин?” саволига “Нодир, Бобир ва Собирларнинг биргаликда тутган хамма балиқлар сони (9+5+6)ни топиш мумкин” деган жавоблари бевосита икки амалли масала билан таништиришни тақозо қилади.

Айириш амали мазмунини очиб берувчи содда масалалар (қолдиқни топиш)га доир ўқувчи билими, кўникма ва малакаларини мустахкамлаш босқичида ортиқча маълумотли қуйидаги кўринишдаги масала-топшириқларни келтириш мумкин.

Масаладаги ортиқча маълумотни аниқланг ва масалани ечинг. “Саватда 8кг, халтачада 5кг олма бор. Саватдан 3кг олма ишлатилди. Саватда неча кг олма қолди?”

Ушбу масалада халтачадаги олма миқдори – ортиқча сон маълумот эканлигини ўқувчи англай олиши керак. Шу ортиқча сон маълумотни ишлатмай ўқувчи ўзига таниш қолдиқни топишга доир масала: “Саватда 8кг олма бор. Саватдан 3кг олма ишлатилди. Саватда қанча олма қолди?” деган масалани ечишга келиб қолади. Бундай масалани ўқувчи еча олади.

Ўқитувчи ушбу топшириқ устида ишлашни давом эттириб, масалада берилган ортиқча маълумотдан фойдаланган холда, шунингдек, масала шартида ёки масала саволида баъзи ўзгаришларни киритиб, турли мазмундаги масалаларни ечиш мумкинлигини ўқувчиларга тушунтириши зарур.

Масалан: юқоридаги топшириқда ўқувчиларга масала саволига эътибор берилмай, масала шартига берилган сон маълумотларга қараб қандай ифодалар тузиш мумкинлиги сўралганда, ўқувчилар қуйидаги ифодаларни тузиши мумкин (бу ишни хар бир ўқувчи якка тартибда мустақил бажаришда умумсинф мухокамасига қўйилади.) 8-3; 5-3; 8+3; 5+3; 8+5; (8-3)+5; 8+(5-3); (8+5)-3. шунда ўқитувчи тузилган хар бир ифода нимани англатишини сўраши шарт. Чунки, масала матни сон маълумотлари ёрдамида тузилган. Ифода масала шартини қаноатлантириши керак. Хақиқатдан хам, “8-3” ифода “саватдаги (8кг) олмадан 3кг ишлатгандан сўнг саватда қолган олма миқдорини билдирса, “5-3” ифода халтачада қанча олма қолганини билдиради” “8+3” ифода эса айнан масала шартида бўлмаган ифода, чунки 8кг – бу саватдаги олма миқдори, 3кг – бу ишлатилган олма миқдори, келтириб қўшилган олма миқдори эмас, шу сабабли ўқувчилар томонидан тузилган “8+3” ифода ушбу масала шартига тегишли эмас. Худди шунингдек, “5+3” ифода хам, айнан шу қаралаётган топшириқ шартига тегишли эмас. “(8-3)+5” ифодани қуйидагича изохлаш мумкин. “8кг – бу саватдаги олмалар массаси, 3кг саватдаги олмалардан ишлатилган олмалар массасини ифодалайди. 5кг эса халтачадаги олмалар массасини билдиради”. Масала матнидаги ортиқча сон маълумотларни аниқлаш ва масала шартини, саволини ўзгартириш орқали турли мазмундаги ўқув топшириқларни бажариш кўникмаси таркиб топади.

Ўқувчилар икки амалли масалалар билан танишаётган даврда шартида маълумотлари ортиқча бўлган масалаларни қараб чиқиши мумкин. Қуйидаги масалани қарайлик:

“Бир тўпда 24м, иккинчи тўпда 6м ортиқ мато бор. Иккинчи тўпда 30м мато бўлса, иккала тўрпда неча м мато бор?”

Ушбу масалаюзасидан ўқитувчи ўқувчиларга: “Масалани диққат билан ўқиб, масала шартида ортиқча сон маълумотни аниқланг. Ўша ортиқча сон маълумотни ишлатмай масалани ечинг!” топшириғини айтади. Бу ерда ўқувчилар икки хил мушохада қилишлари мумкин. Биринчидан, агар масала матнида “иккинчи тўпда ундан 6м ортиқ мато бор” деган ибора ортиқча бўлса, у холда юқоридаги масала ўқувчилар учун таниш йиғиндини топишга доир содда масалага келиб қолади: “Бир тўпда 24м, иккинчи тўпда 30м мато бўлса, иккала тўпда неча м мато бор?”

Ушбу масаланинг қисқача шарти қуйидагича берилиши мумкин:

?

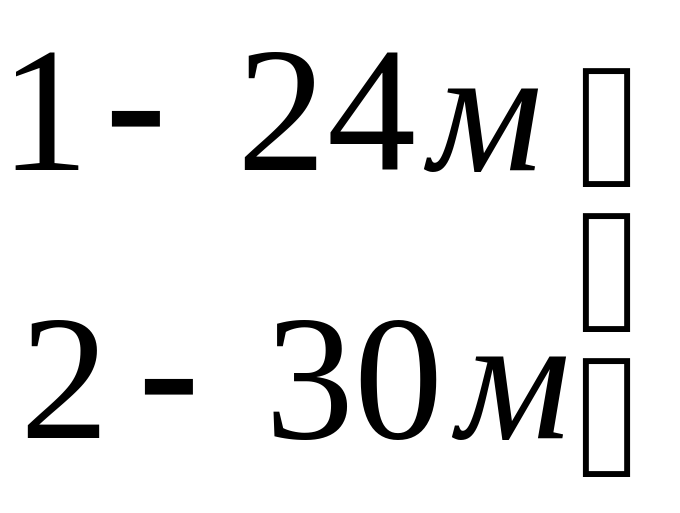Иккинчидан, агар юқоридаги берилган масалада “иккинчи тўпда 30м мато бўлса” ибораси ортиқча маълумот бўлса, у холда масала ўқувчи эндигина ечишни ўрганаётган икки амалли масалага айланади. “Бир тўпда 24м мато, иккинчи тўпда ундан 6м ортиқ мато бор. Иккала тўпда неча м мато бор?”

Масаланинг қисқа шартини қисқа ёзув шаклида қуйидагича ифодалаш мумкин:

?

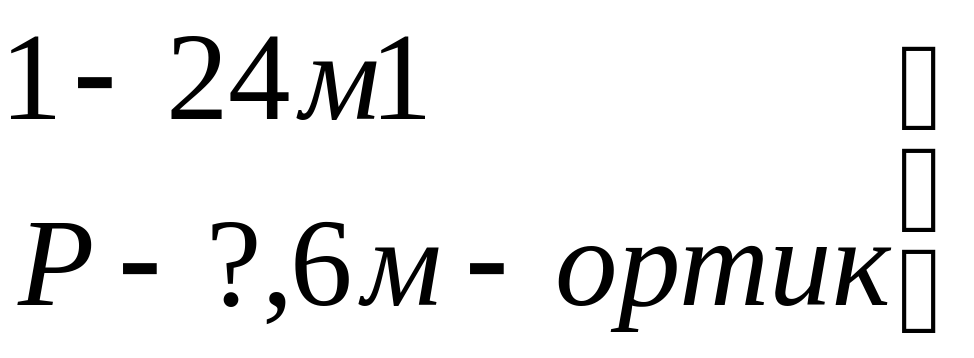Берилган масалада ортиқча маълумот, бир томондан, ўқувчининг масала ечимини излашга туртки бўлади, чунки “иккинчи тўпда 30м мато бор” деган жумла, ўз навбатида (24+6)ни ифодалайди, яъни, иккинчи тўпда биринчи тўпдаги 24м матодан 6м ортиқ мато борлигини билдиради. Бу билан ўқувчининг иккала икки амалли масала ечимини топишига ёрдам бўлади.

Худди шунингдек, “та кам” муносабати иштирок этган тўғри масалаларда хам шартига ортиқча маълумотли масалаларни қараш орқали ўқувчиларнинг икки амалли масалаларни мустахкамлашига ёрдам беради.

Арифметик амал хоссалари (сонга йиғиндини қўшиш, йиғиндига сонни қўшиш, сондан йиғиндини айириш, йиғиндини сондан айириш, сонни йиғиндига кўпайтириш; кўпайтмани сонга кўпайтириш ва х.ку.) ўрганишда хам шартида сон маълумотлари ортиқча бўлган масалалардан фойдаланиш орқали ўқувчининг ижодий фаоллиги ошади, мантиқий мустақил фикрлаши ўсади. 2-синфда ўқувчиларнинг йиғиндидан сонни айиришга доир билимларини мустахкамлаш мақсадида қуйидаги топшириқни бериш мумкин: “Масалани диққат билан ўқинг. Ортиқча сон маълумотни аниқланг. Масалани ечинг. Мебел дуконига 15та шкаф, 25та кроват, 40та стул, шкаф ва кроват биргаликда нечта бўлса, шундан 8та кам стол келтирилди. Дўконда нечта стол келтирилган?” Масала қисқа шартининг схема кўриниши ёки қисқа ёзувда ифодаланиши ўқувчининг масаладаги ортиқча маълумотни тез аниқлашига ёрдам беради.

ШКАФ КРОВАТ СТУЛ

15ТА 25ТА 40ТА

СТОЛ?,

8ТА КАМ

ёки

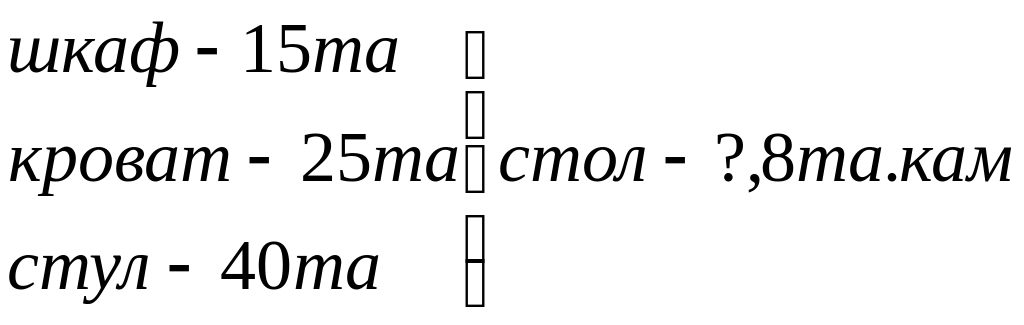
Ушбу масалада стуллар миқдори(40) – ортиқча маълумот. Ўқувчилар бу ортиқча маълумотни ишлатмай, иккинчи синфда йиғиндидан сонни айириш хоссасини мустахкамлашга доир масалага келиб қоладилар: “Мебел дўконига 15та шкаф, 25та кроват, шкаф ва кроват биргаликда нечта бўлса, шундан 8та кам стол келтироишди. Дўконга нечта стол келтирилган? ”. Ушбу масала ечилгач, ўқувчилар диққатини ортиқча маълумоти қатнашган холда масала шартида баъзи ўзгаришлар ёки масала саволини ўзгартирган холда бир қатор янги мазмундаги ўқув топшириқларини ўқувчиларга хавола қилиш мумкин. Берилган топшириқ юзасидан “масала саволи талаб қилинадиган ифода тузинг”, “берилган сон маълумотлардан яна қанақа ифодаларни тузиш мумкин?”, “тузилган ифодалар нимани билдиради?” каби ўқув топшириқлари ўқувчи тафаккурини чархлайди, уни изланишга, топқирликка чорлайди.

Х У Л О С А

Ушбу ўқув қўлланмада бошланғич синф математика дарслиги бўйича назорат ишлари баён этилган мавзулар бўйича ёзма назорат ишлари ҳамда тестлар берилган. Албатта, ўқувчиларнинг билимлари назорат ва тестларни бажариш орқали аниқланади. Натижада ўқувчиларнинг билими қай даражада эканлиги аниқланиб, тегишли чора - тадбирлар тузилади.

Хулоса қилиб шуни айтиш мумкинки, ушбу ўқув қўлланма олий ўқув юрт талабалари, бошланғич синф ўқитувчиларига ҳам назарий, ҳам амалий жихатдан ёрдам беради, деб ўйлаймиз.

ФОЙДАЛАНИЛГАН АДАБИЁТЛАР РЎЙХАТИ

1. М.Ахмедов, Р.Ибрагимов, Н.Абдурахмонова, М.Жумаев “1 – синф математика дарслиги” Т. “Ўқитувчи” 1996й.

2. Бикбаева Н.У.,Ахмаджонов И., Янгибаева Е.Я., Адамбекова Г.А., 2 – синф математика дарслиги.Т. “Ўқитувчи” 1997й.

3. Бикбаева Н.У. ва бошқалар. 3– синф математика дарслиги Т. “Ўқитувчи” 1997й

4. Бикбаева Н.У. ва бошқалар. 4 – синф математика дарслиги Т. “Ўқитувчи” 1998й.

5. Бикбаева Н.У.Гирфанова К. “Назорат ишлари” Т. “Бошланғич таълим” № 6 2002й.

6. Мирзаахмедов М. “Математикадан ёзма назорат ишлари” №2. 2006й.

МУНДАРИЖА

Кириш...................................................................................................................5

1 § Математикадан ёзма назорат ишлари........................................6

2 § Дарслик бўйича тест саволлари ...............................................10

3 § Уч хонали сонларни рақамлаш..................................................11

4 § Назорат ишлари..........................................................................12

5 § Ностандарт масала – топшириқлар .........................................26

6 § Ортиқча маълумотга эга бўлган масала-топшириқлар............33

Хулоса....................................................................................................37

Фойдаланилган адабиётлар рўйхати..................................................38

Тошкент Вилоят Давлат педагогика институти 2008й. январ ойида бўлиб ўтган илмий кенгаш томонидан нашрга тавсия этилган

Мухаррир: М.Шомирзаева

40