Trigonometry (Sum and Differece Formulas)

Sum and Difference Formulas in Trigonometry

Introduction

The students will learn

• trigonometric ratios of the sum or difference of two arcs,

• half-angle formulas,

• conversion and inverse conversion formulas .

Trigonometric Ratios of The Sum or Difference of Two Arcs

Theorem 1.4

Theorem 1.5

Theorem 1.6

Theorem 1.7

Theorem 1.4

If a and b are two real numbers, then

Proof-1

1. cos(a+b) = cos a . cos b - sin a . sin b

Example-1

Proof-2

2. cos(a-b) = cos a . cos b + sin a . sin b

Example-2

Proo f -3

3. sin(a+b) = sin a . cos b + cos a . sin b

Example-3

Proof-4

4. sin(a-b) = sin a . cos b - cos a . sin b

Example-4

BACK

Theorem 1.5

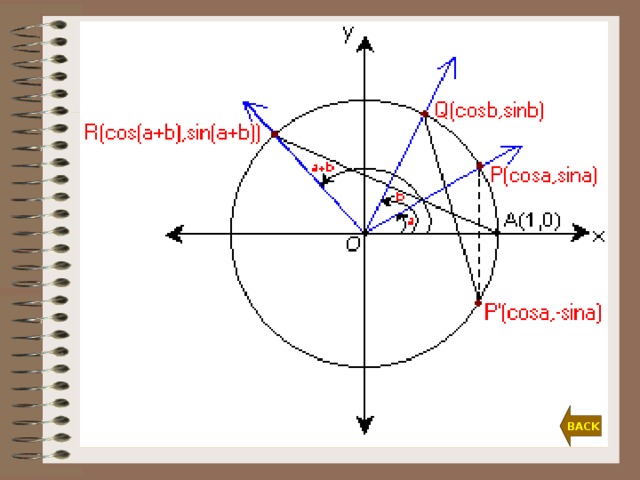
Proof-1 cos(a+b) = cos a . cos b - sin a . sin b

Full Screen

Since the lenghts of arc AP and AP’ are equal then  AR  =  P’Q  .

If is the distance between two points (x 1 ,y 1 ) and (x 2 ,y 2 ),

then the distance formula will be as follow s then

 AR  =  P’Q  AR  2 =  P’Q  2

(cos(a+b)-1) 2 + (sin(a+b)- 0) 2 = (cos a – cos b) 2 + (sin b + sin a) 2

• (cos(a+b)-1) 2 + (sin(a+b)- 0) 2 = (cos a – cos b) 2 + (sin b + sin a) 2

cos 2 (a+b) – 2cos(a+b) + 1 + sin 2 (a+b) = cos 2 a –2cosa.cosb + cos 2 b + sin 2 b + 2sina. sinb + sin 2 a

2 – 2cos(a+b) = 2 – 2cosa.cosb + 2sinb.sina

cos(a+b) = cosa. cosb – sina. sinb

BACK

Example-1

Full screen

BACK

Example-1:

cos 75 o = ?

Solution-1

Solution-1:

cos 75º = cos ( 45º + 30º )

= cos 45º.cos 30º - sin 45º. sin 30º

=

=

BACK

Proof-2 cos(a-b) = cos a . cos b + sin a . sin b

Since cos(a+b) = cosa . cosb – sina . s inb is valid far all real numbers a and b,

t hen cos(a+(-b)) = cosa . cos(-b) – sina . sin(-b)

cos(a-b) = cosa . cosb + sina . sinb

BACK

Example-2

Example-2:

cos 15 o = ?

Solution-2

Solution-2:

cos 1 5 º = cos ( 45 º - 30 º )

= cos 45 º .cos 30 º + sin 45 º . sin 30 º

=

=

BACK

Proof-3 sin(a+b) = sin a . cos b + cos a . sin b

We can write sine in terms of cosine by using reduction formulas. Hence,

sin(a+b) = sin a . cos b + cos a. sin b

BACK

Example-3

Example-3:

sin 105 o = ?

Solution-3

Solution-3:

sin 10 5º = cos ( 60 º + 45 º )

= sin 60 º.cos 45 º + cos 60 º. sin 45 º

=

=

BACK

Proof-4 sin(a+b) = sin a . cos b - cos a . sin b

Since the equality sin(a+b) = sin a . cos b + cos a. sin b is valid for all real numbers a and b, by writing –b instead of b, we get

sin(a+ (-b) ) = sin a . cos (- b ) + cos a. s in (- b ) then

sin(a+b) = sin a . cos b - cos a . sin b

BACK

Example-4

Example-4:

sin 15 o = ?

Solution-4

Solution-4:

sin 1 5º = cos ( 60 º - 45 º )

= sin 60 º.cos 45 º - cos 60 º. sin 45 º

=

=

BACK

Theorem 1.5

1. If a, b and a+b real numbers different from  /2+k  , k  Z, then

Proof-5

Example-5

2. If a, b and a-b real numbers different from  /2+k  , k  Z, then

Proof-6

Example- 6

BACK

Theorem 1.6

Proof-5

BACK

Example-5

Example-5:

Let  and  be two acute angles. If sin  = 3/5 and cos  = 5/13, then find tan(  +  ).

Solution-5

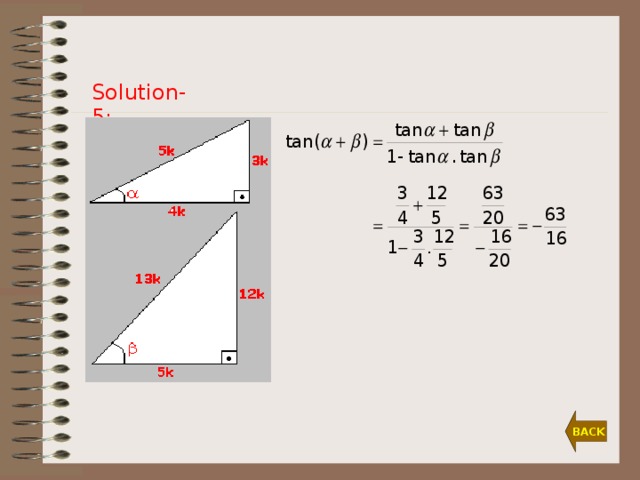
Solution-5:

BACK

Proof-6

2. If we write –b instead of b in the previous equality then,

BACK

Example-6

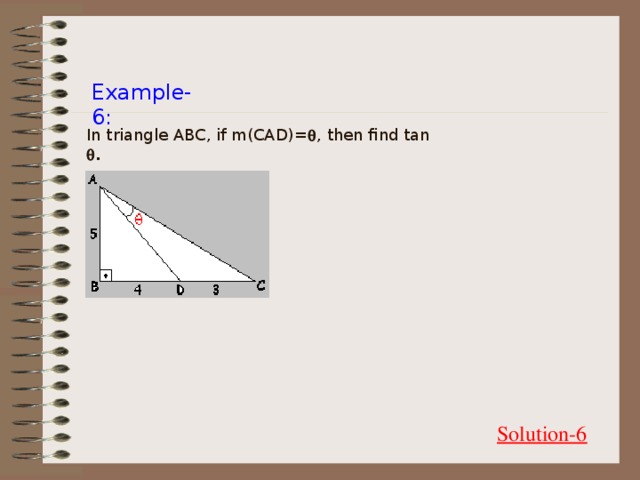
Example-6:

In triangle ABC, if m(CAD)=  , then find tan  .

Solution-6

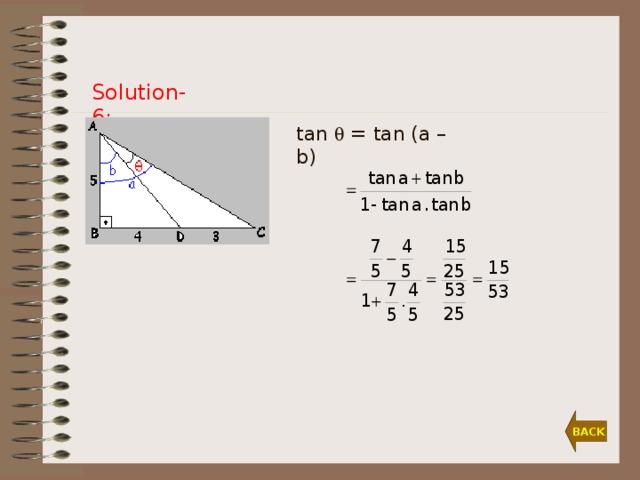
Solution-6:

tan  = tan (a – b)

BACK

Theorem 1.6

1. If a, b and a+b real numbers different from k  , k  Z, then

Proof-7

Example-7

2. If a, b and a-b real numbers different from k  , k  Z, then

Proof-8

Example-8

BACK

Theorem 1.7

Proof-7

BACK

Example-7

Example-7:

In the adjoining figure  AB  = 4,  BC  = 3,  AD  = 12 and m(ABC)=90º, m(CAD)=90º, m(CED)=90º. Find cot  , if m(DCE) =  .

Solution-7

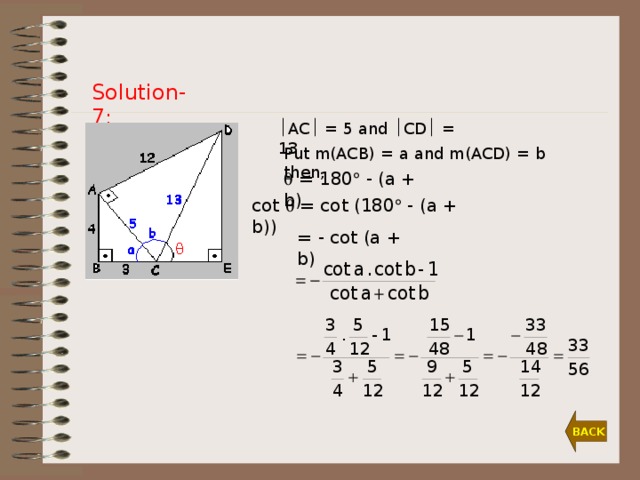
Solution-7:

 AC  = 5 and  CD  = 13.

Put m(ACB) = a and m(ACD) = b then,

 = 180  - (a + b)

cot  = cot (180  - (a + b))

= - cot (a + b)

BACK

Proof-8

2. If we write –b instead of b in the previous equality then,

BACK

Example-8

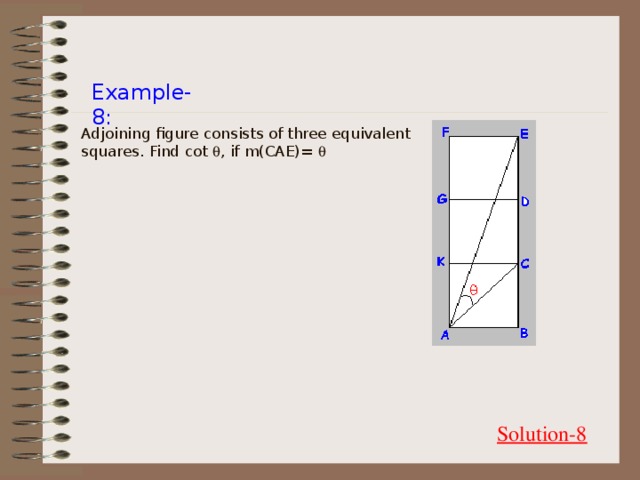
Example-8:

Adjoining figure consists of three equivalent squares. Find cot  , if m(CAE)= 

Solution-8

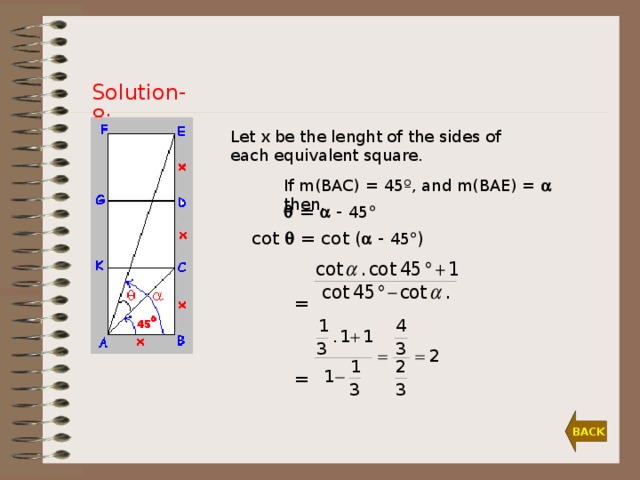
Solution-8:

Let x be the lenght of the sides of each equivalent square.

If m(BAC) = 45º, and m(BAE) =  then,

 =  - 45 

cot  = cot (  - 45  )

=

=

BACK

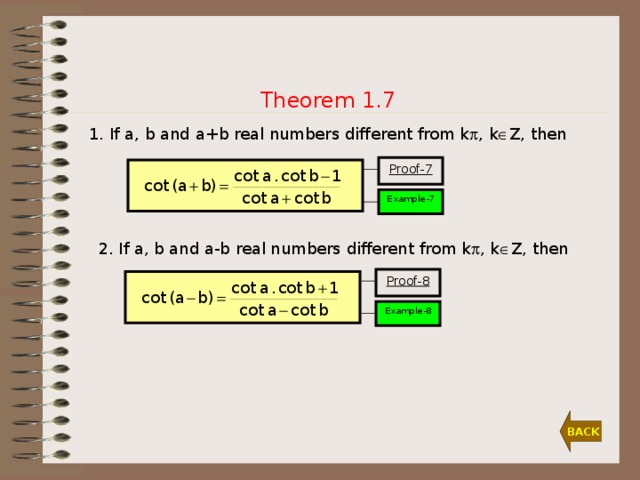
Theorem 1.7

1. If a, b and a+b real numbers different from k  , k  Z, then

Proof-7

Example-7

2. If a, b and a-b real numbers different from k  , k  Z, then

Proof-8

Example-8

BACK