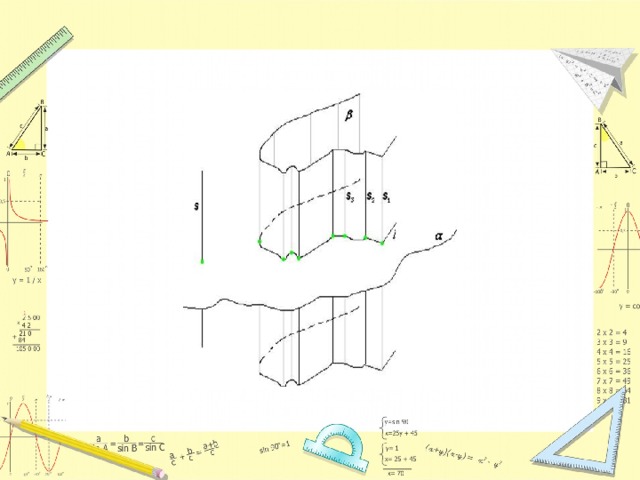
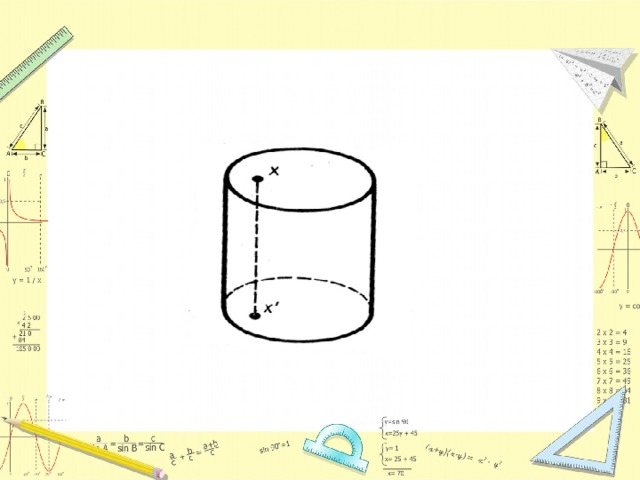
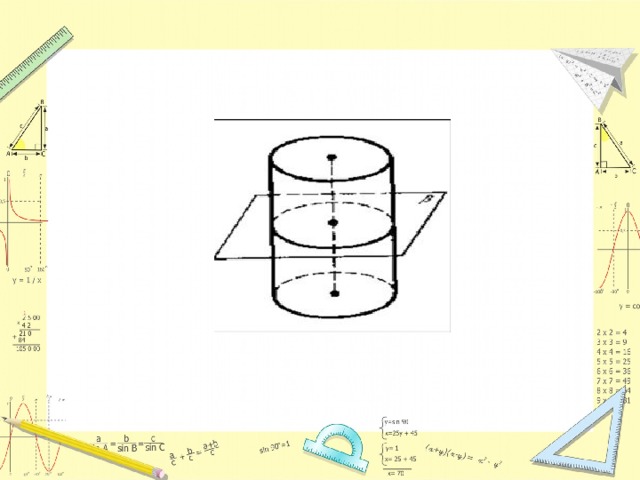
СЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ. ЭЛИПС.

Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой) цилиндрической поверхностью, а с торцов двумя плоскими параллельными основаниями. Оба основания цилиндра равны, также равны между собой и все образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между плоскостями оснований.
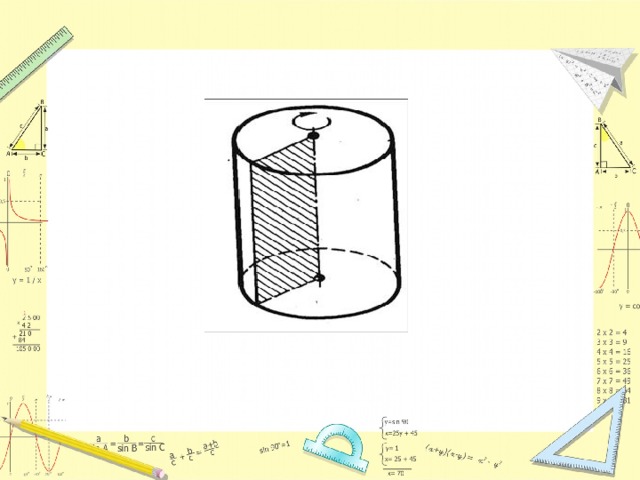
Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а.