Презентация для 5 класса, разработана для проведения кружкового занятия на тему «Деление окружности на части. Построение правильных многоугольников» научит учащихся на уроке математики делению этой геометрической фигуры на 3, 6 частей, и построению правильного шестиугольника и треугольника. Данное пособие можно использовать для проведения интегрированного урока по математике и изобразительному искусств, объединив в одном уроке работу с геометрическим материалом и построением орнаментов с использованием циркуля для вырисовывания узоров в круге. Содержит информационный материал по теме, что поможет расширить кругозор учащихся и повысить познавательный интерес.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
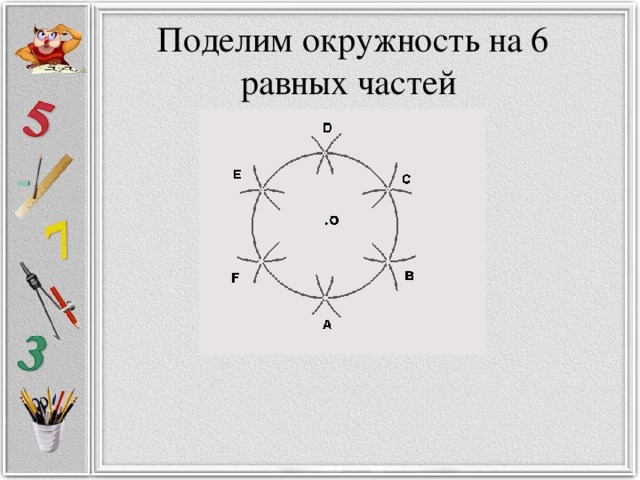
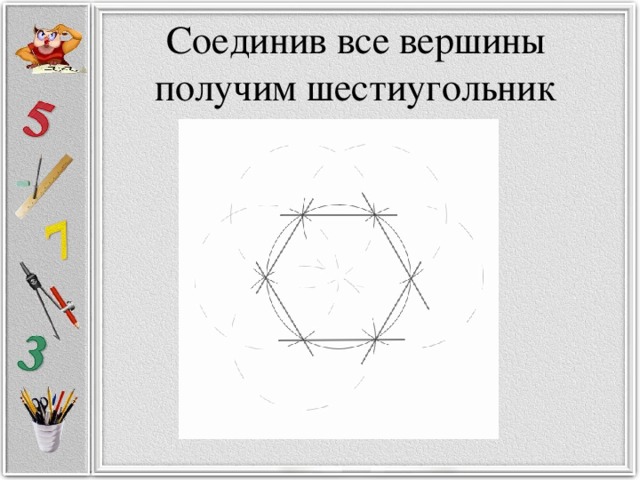
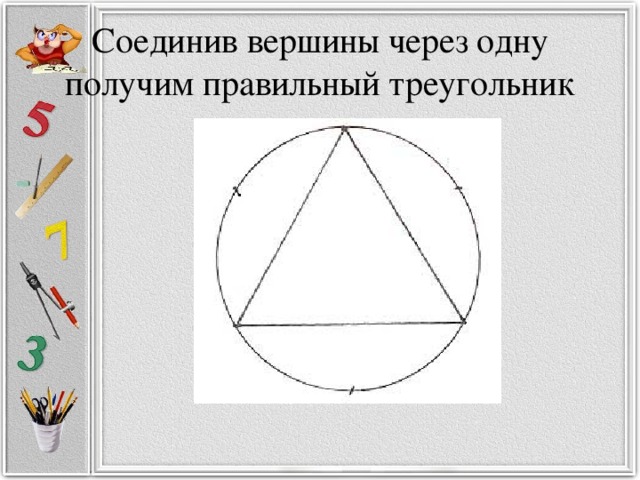
Разработка кружкового занятия "Построение правильных многоугольников (с помощью окружности). Деление окружности на части." .
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Разработка кружкового занятия "Построение правильных многоугольников
(с помощью окружности). Деление окружности на части." . »
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1800 руб.
3000 руб.
1720 руб.
2860 руб.
1690 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства