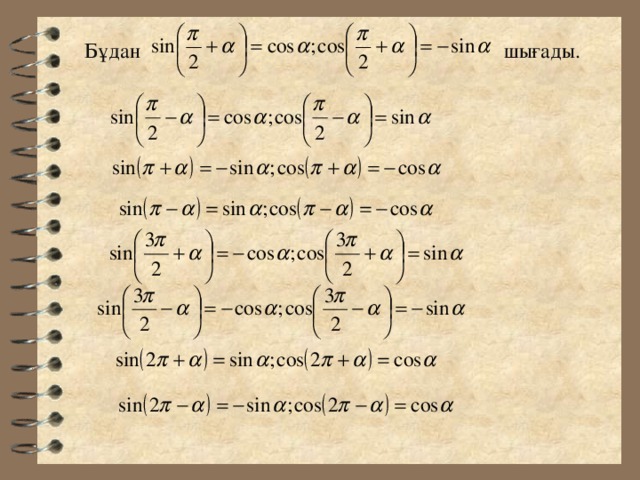Я учитель математики и информатики первой категории. Я горжусь своей профессией. Окончила педагогический институт имени Ш.Уалиханова в городе Кокшетау 1995 году. Я за свой 19 лет стажа накопила много опыта благодаря своим наставникам, учителям Ауезовской СШ Уалихановского района Северо-Казахстанской области Нугумановой Мариям Шаяхметовны и Ауталипова Мухтара Ауталиповича. Я работаю в данной Тургайской СШ с 2014 года. Я проводила районный семинар естественного математического цикла, районный мастер-класс. Участвовала на областном семинаре, на областной конференции Последние курсы по повышению квалификации в Петропавловском ИПК феврале 2014 г, в Астане в октябре 2014.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
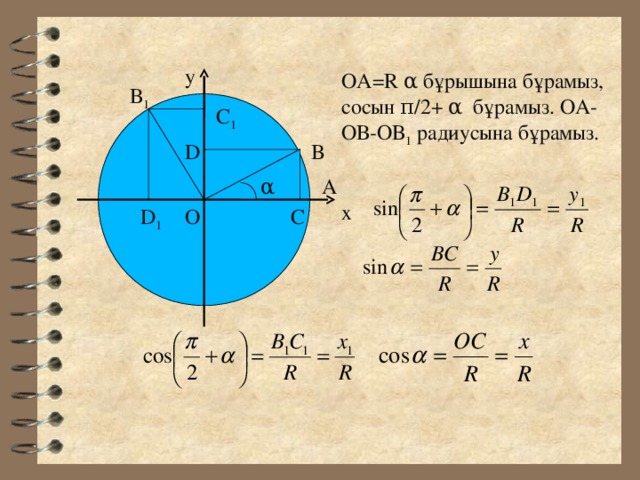
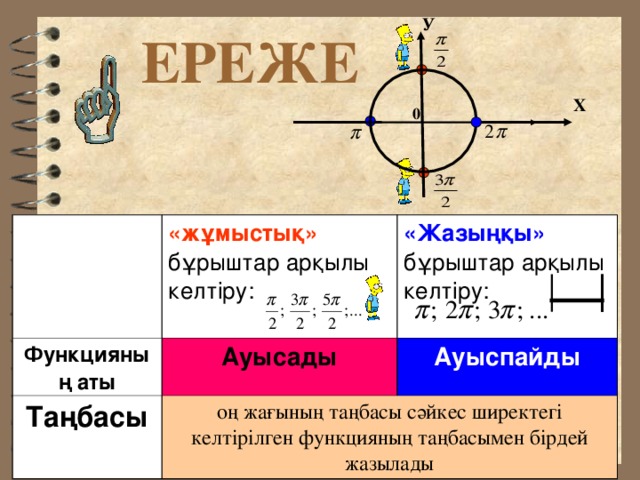
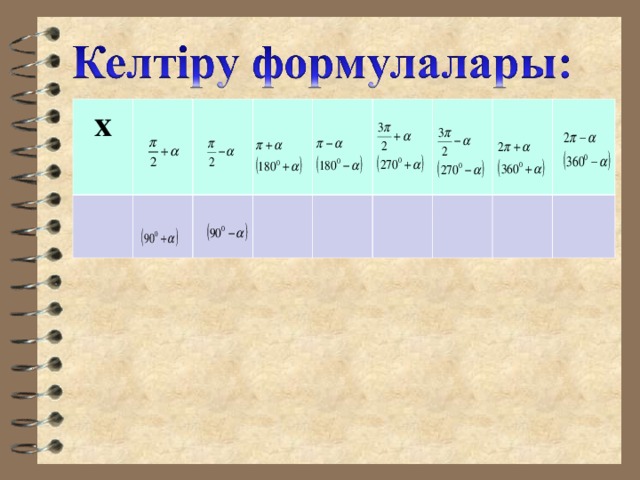
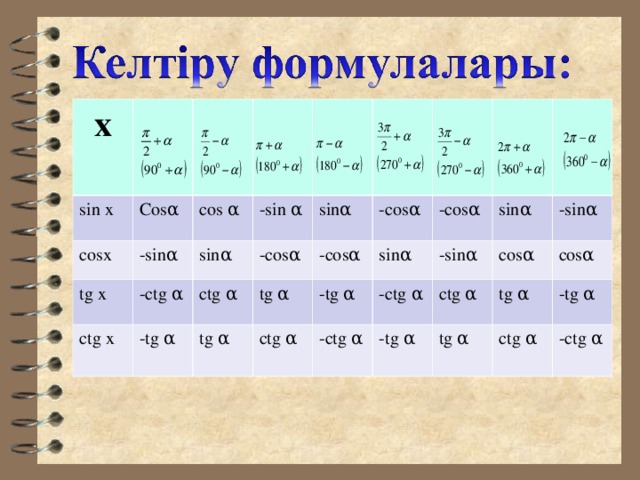
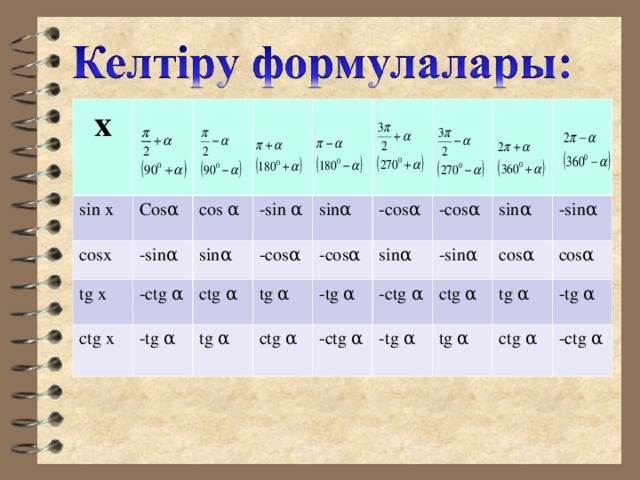
Презентация урока " Келтіру формулалары"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«презентация урока " Келтіру формулалары" »
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
1740 руб.
2480 руб.
2220 руб.
3170 руб.
2020 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства