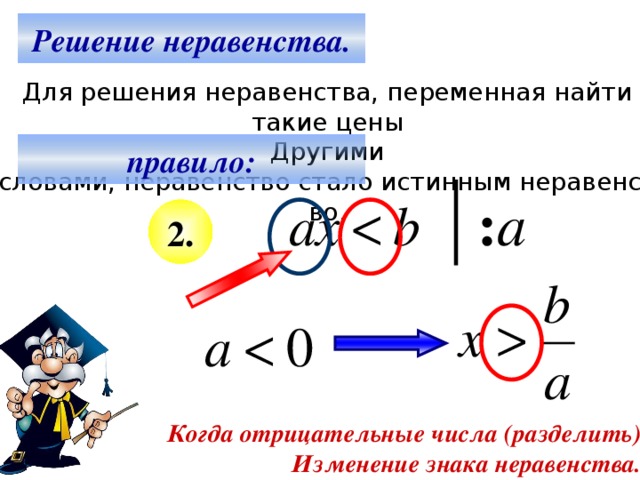
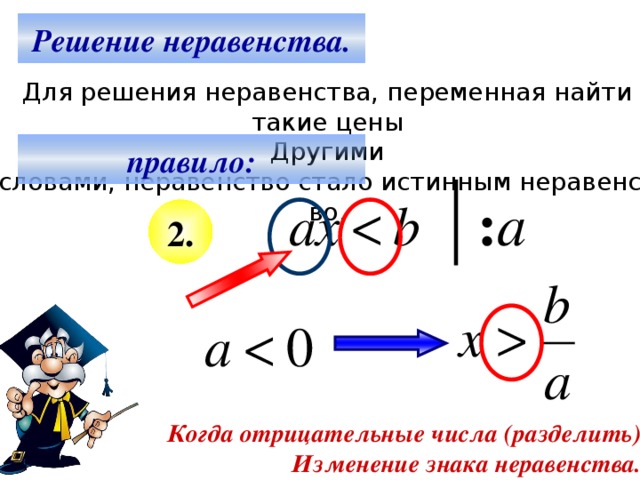
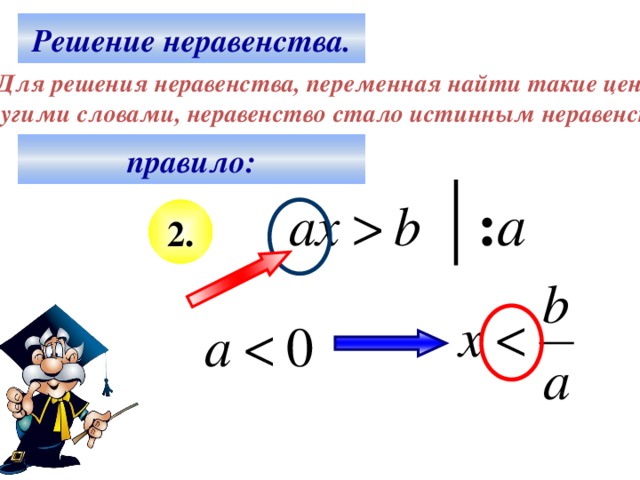
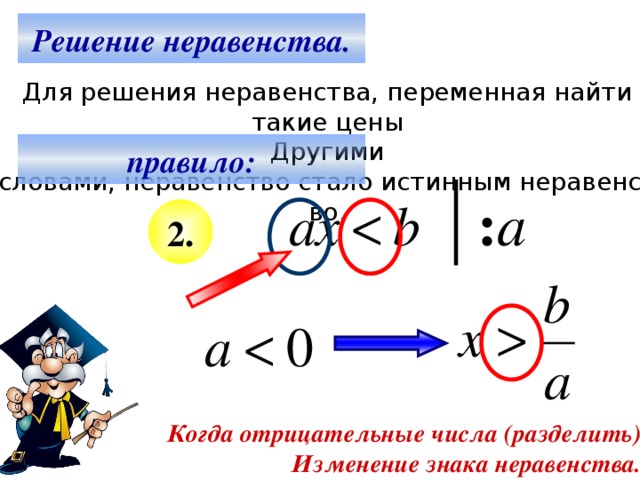
Пусть в результате преобразований исходного неравенства мы пришли к следующему неравенству:
(x-3)2*(x-7)3*(x+1) / (x-2)*(x+4)2 >= 0.
Обратите внимание, что в каждом из сомножителей переменная стоит на первом месте, то есть (х-2) а не (2-х).К такому виду всегда можно привести данные скобки умножая их на -1, и при этом не забывая менять знак.
Теперь нам необходимо на числовой прямой отметить все точки в которых в числителе или знаменателе получается нуль. Так как неравенство не строгое (>=), то нули числителя отмечаем обычными точками, а нули знаменателя выколотыми точками. Если бы неравенство было строгим, то все точки надо было бы рисовать выколотыми. Эти точки разбили нашу прямую на несколько интервалов.
Теперь надо расставить знаки. В самый правый интервал ставим знак «плюс». Далее знаки в каждом промежутке расставляются в соответствии со следующим правилом.
- Знак меняется, если у скобки была нечетная степень.
- Знак не меняется, если у скобки была четная степень.
Например, у нас. Сначала был знак «плюс». Далее точка 7. Смотрим неравенство, у нас там множитель с семеркой (х-7)^3 имеет третью степень. Тройка нечетное число, значит знак меняем и записываем его над промежутком. Следующая точка 3. Смотрим неравенство. Тройка имеется в множителе (x-3)^2. Степень четная значит знак остается таким же «минус». И так продолжаем до конца, пока у каждого промежутка не будет свой знак.
Получится следующая картинка.