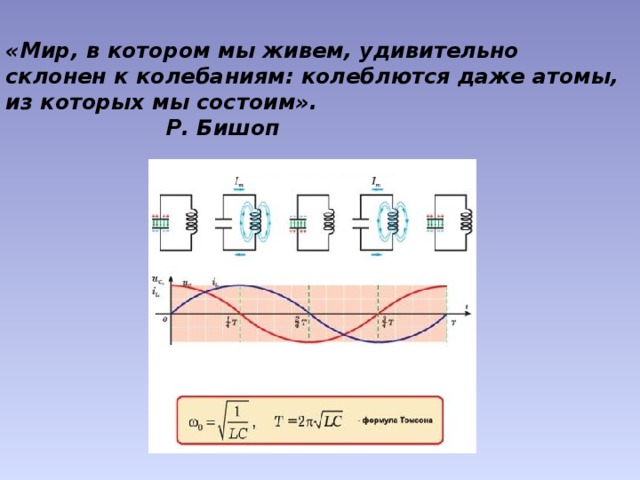
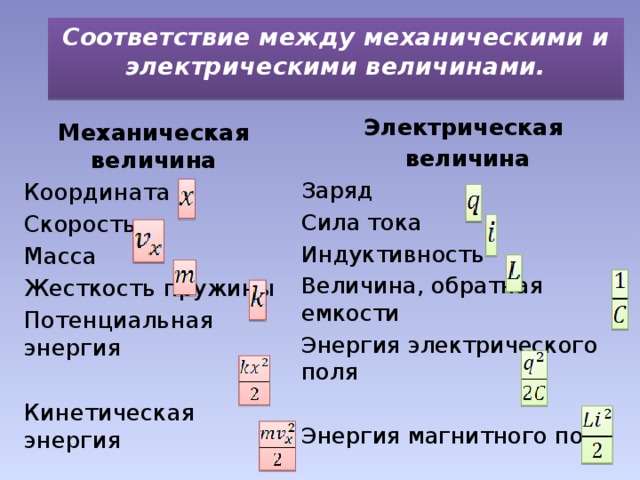
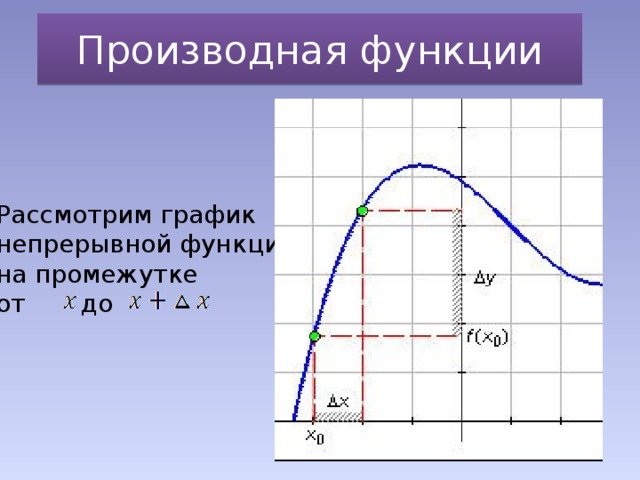
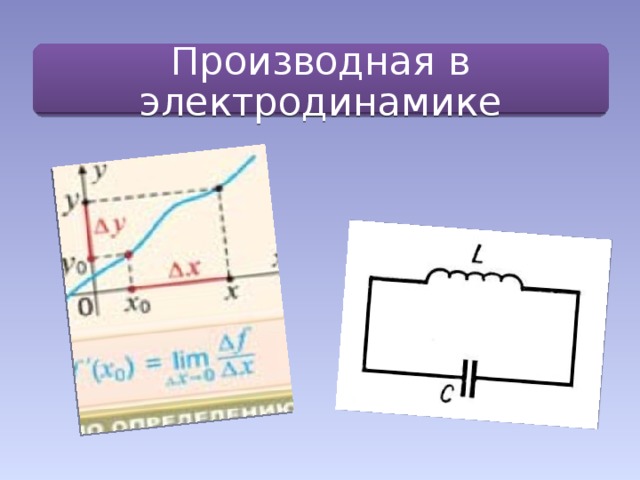
Интеграция обучения дает ученику те знания, которые отражают связанность отдельных частей мира как системы, учит представлять мир как единое целое, в котором все элементы взаимосвязаны. В данной презентации интегрированного урока по теме «Производная в электродинамике» повторяется принцип работы колебательного контура, устанавливается соответствие между механическими и электрическими величинами, вводятся основные понятия электродинамики. Для вывода уравнения электромагнитных колебаний дается определение производной, рассматривается ее физический смысл. Определяется роль математики в физических процессах, решаются задачи по теме «Электромагнитные колебания». На таком уроке создаются благоприятные условия для развития самых разных интеллектуальных умений учащихся.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация. Производная в электродинамике
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
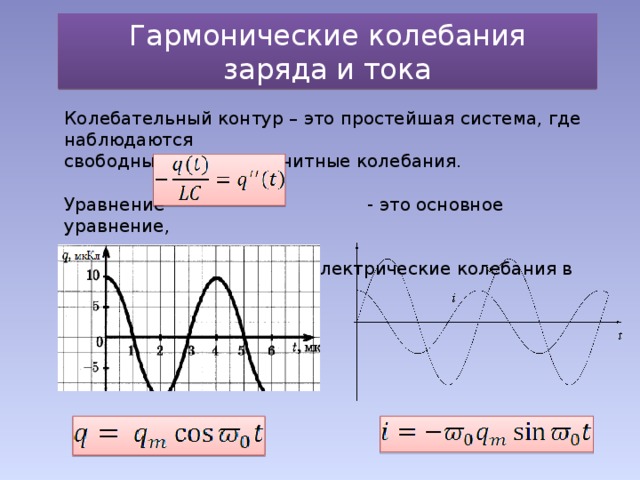
«Презентация. Производная в электродинамике»
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
2000 руб.
2860 руб.
2220 руб.
3170 руб.
2100 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства