
Преобразование графика квадратичной функции
Работа учителя математики
МОУ СОШ №3, с.Кочубеевское
Прокопенко Н.В.

Цель урока:
рассмотреть виды преобразований
графика квадратичной функции.
Задачи урока:
• ознакомить учащихся с графиками частных видов квадратичной функции – функций у = ах 2 , у = ах 2 + n , y = a (x – m) 2 ; у=a (x – m) 2 - n .
• научить выполнять преобразования графиков квадратичной функции.
- привитие практических умений и навыков по построению графиков.

Квадратичной функцией называется функция, которую можно задать формулой вида у=ах 2 +вх+с, где х - независимая переменная, а, в и с – некоторые числа, причем а ≠ 0.
 0 ветви параболы у = ах 2 направлены … . вверх 7).Если а отрицательные" width="640"
0 ветви параболы у = ах 2 направлены … . вверх 7).Если а отрицательные" width="640"
Заполни пропуски …
1) .Функция у = a х 2 + bx + c, где а, b, c – заданные действительные числа, а 0, х – действительная переменная, называется … функцией.
квадратичной
2).График функции у = ах 2 при любом а 0 называют … .
параболой
3).Функция у = х 2 является … (возрастающей, убывающей) на промежутке х 0.
убывающей
4).Значения х, при которых квадратичная функция равна нулю, называют … функции.
нулями функции
5).Точку пересечения параболы с осью симметрии называют … параболы.
вершиной параболы
6).При а 0 ветви параболы у = ах 2 направлены … .
вверх
7).Если а
отрицательные
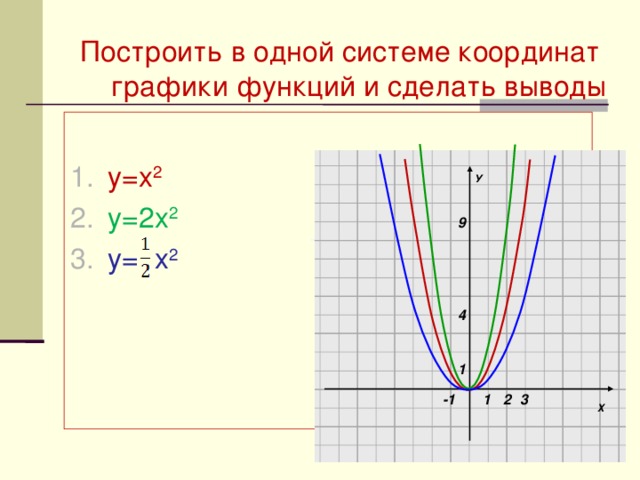
Построить в одной системе координат графики функций и сделать выводы
У
9
4
1
Х
-1
3
2
1

Выводы:
График функции у=2х 2 можно получить из параболы у=х 2 растяжением вдоль оси Оу в 2 раза;
График функции у= х 2 можно получить из параболы у=х 2 сжатием относительно оси Оу в 2 раза;
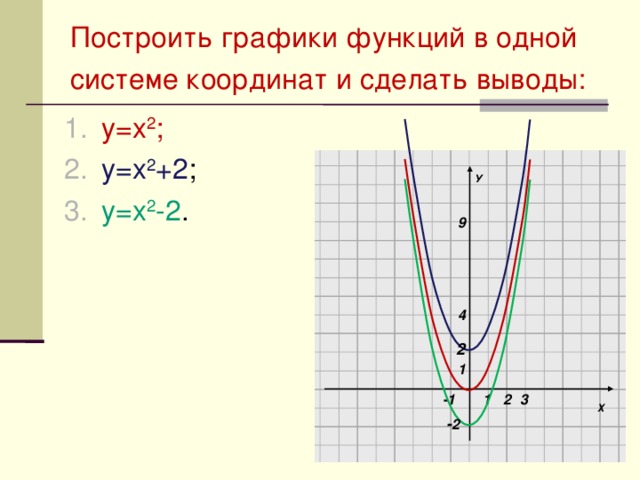
Построить графики функций в одной
системе координат и сделать выводы:
- у=х 2 ;
- у=х 2 +2 ;
- у=х 2 -2 .
У
9
4
2
1
Х
2
3
-1
1
- 2

Выводы:
- График функции у=х 2 +2 – парабола, полученная в результате сдвига вверх на 2единицы вдоль оси О у графика функции у=х 2 ;
- График функции у=х 2 +2 – парабола, полученная в результате сдвига вниз на 2 единицы вдоль оси О у графика функции у=х 2 .
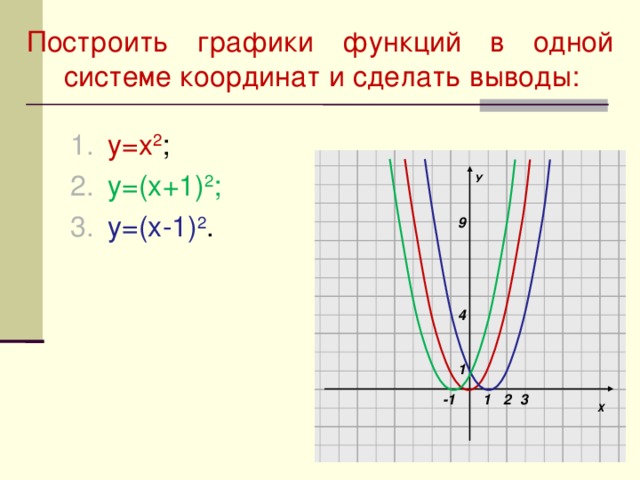
Построить графики функций в одной системе координат и сделать выводы:
- у=х 2 ;
- у=(х+1) 2 ;
- у=(х-1) 2 .
У
9
4
1
Х
3
-1
2
1

Выводы
- График функции у=(х+1) 2 – парабола, полученная в результате сдвига влево на 1 единицу вдоль оси Ох графика функции у=х 2 ;
- График функции у=(х-1) 2 – парабола, полученная в результате сдвига вправо на 1 единицу вдоль оси Ох графика функции у=х 2 .
Преобразования графика квадратичной функции
Преобразования
графика
Растяжение,
сжатие
Симметрия
Сдвиг
 1, сжатие в 1 /k раз, если 0 у= f( х ) + m Сдвиг вдоль оси ОУ на m единиц вверх, если m 0; на ImI единиц вниз, если m у= f( х- n) Сдвиг вдоль оси ОХ на а единиц вправо, если n 0; на InI единиц влево, если n
1, сжатие в 1 /k раз, если 0 у= f( х ) + m Сдвиг вдоль оси ОУ на m единиц вверх, если m 0; на ImI единиц вниз, если m у= f( х- n) Сдвиг вдоль оси ОХ на а единиц вправо, если n 0; на InI единиц влево, если n
Выводы
Функция
у=- f( х )
Преобразование графика функции у= f( х )
Симметрия относительно оси ОХ
у=а f( х )
Растяжение графика вдоль оси ОУ в к раз, если к 1, сжатие в 1 /k раз, если 0
у= f( х ) + m
Сдвиг вдоль оси ОУ на m единиц вверх, если m 0; на ImI единиц вниз, если m
у= f( х- n)
Сдвиг вдоль оси ОХ на а единиц вправо, если n 0; на InI единиц влево, если n

ПРОВЕРЬ СЕБЯ.
График какой функции изображен на рисунке?
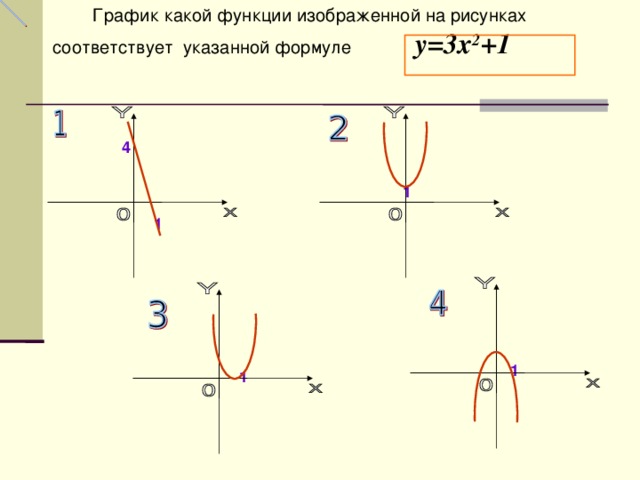
График какой функции изображенной на рисунках соответствует указанной формуле у =3 х 2 +1
1
1
4
1
1
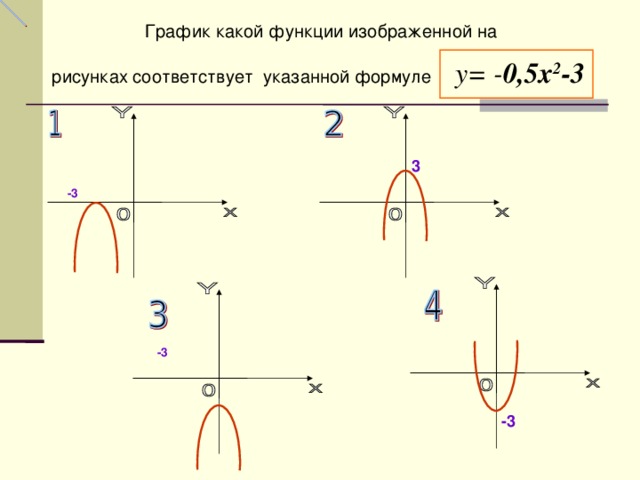
График какой функции изображенной на рисунках соответствует указанной формуле у = - 0,5 х 2 -3
3
-3
-3
-3
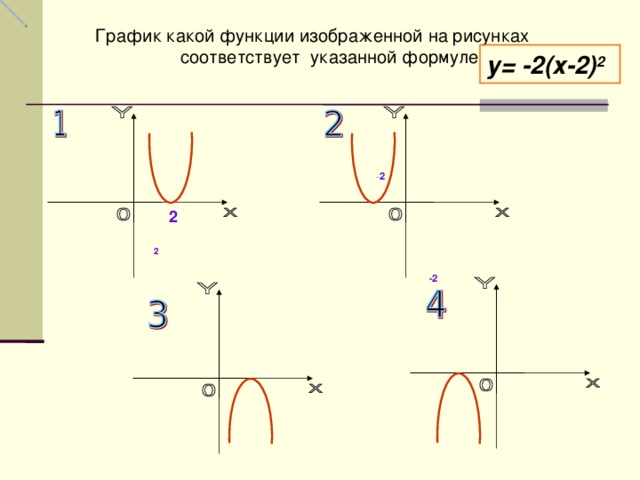
График какой функции изображенной на рисунках соответствует указанной формуле
у = -2( х -2) 2
- 2
-2
2
2
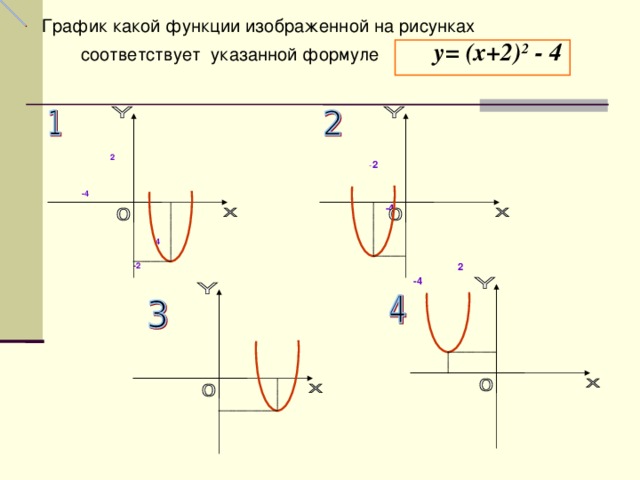
График какой функции изображенной на рисунках соответствует указанной формуле у = ( х +2) 2 - 4
- 2
-4
2
-4
2
-4
4
-2
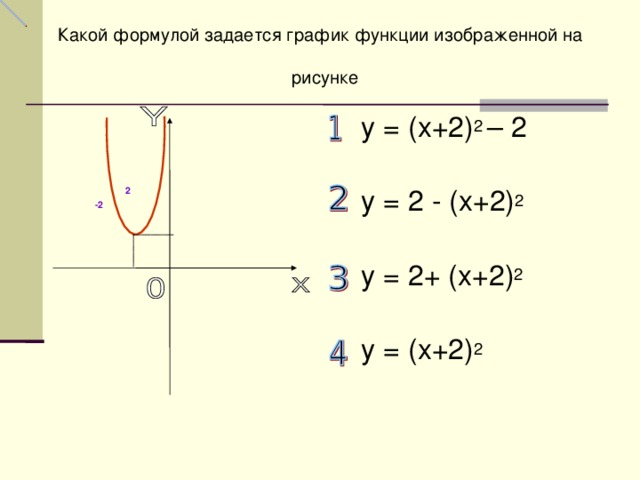
Какой формулой задается график функции изображенной на рисунке
у = (х+2) 2 – 2
у = 2 - (х+2) 2
у = 2+ (х+2) 2
у = (х+2) 2
2
- 2
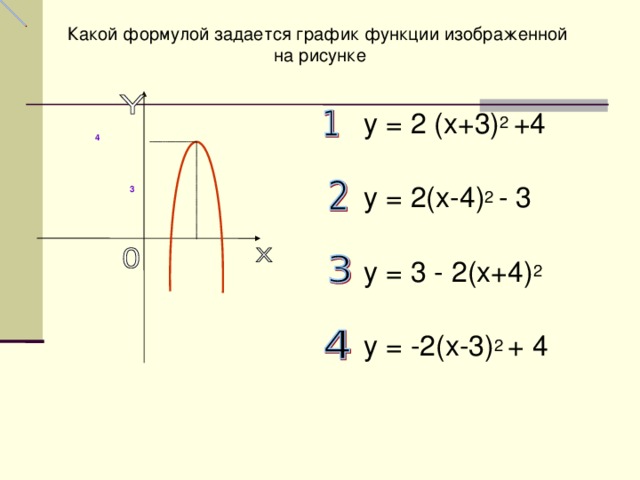
Какой формулой задается график функции изображенной
на рисунке
у = 2 (х+3) 2 +4
у = 2(х-4) 2 - 3
у = 3 - 2(х+4) 2
у = -2(х-3) 2 + 4
4
3
Ответы:
3
2
3
3
2
3
4

Спасибо за урок! Желаю удачи!

Список использованной литературы.
1. Макарычев Ю.Н.и др. под редакцией Теляковского С.А. Алгебра 9 класс. М.: Просвещение, 2013.
2. А.П.Ершова В.В.Голобородько. Самостоятельные и контрольные работы. Алгебра. Геометрия 9 класс. М.«Илекса», 2010.
3.П.И.Алтынов. Тесты по алгебре. 9 класс. М.«Экзамен», 2012.
Интернет – ресурсы.
www.testent.ru
http://www.uchportal.ru/load/24-1-0-22420
f estival.1september.ru/articles/534282/



 0 ветви параболы у = ах 2 направлены … . вверх 7).Если а отрицательные" width="640"
0 ветви параболы у = ах 2 направлены … . вверх 7).Если а отрицательные" width="640"







 1, сжатие в 1 /k раз, если 0 у= f( х ) + m Сдвиг вдоль оси ОУ на m единиц вверх, если m 0; на ImI единиц вниз, если m у= f( х- n) Сдвиг вдоль оси ОХ на а единиц вправо, если n 0; на InI единиц влево, если n
1, сжатие в 1 /k раз, если 0 у= f( х ) + m Сдвиг вдоль оси ОУ на m единиц вверх, если m 0; на ImI единиц вниз, если m у= f( х- n) Сдвиг вдоль оси ОХ на а единиц вправо, если n 0; на InI единиц влево, если n


























