Для подготовки к ЕГЭ 2015 года по демоверсии ЕГЭ 2015 года. С помощью этих презентаций выпускники смогут самостоятельно подготовиться к выполнению задания №4. Формула Пика позволит выпускникам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами. Примеры взяты из открытого банка заданий по математике.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
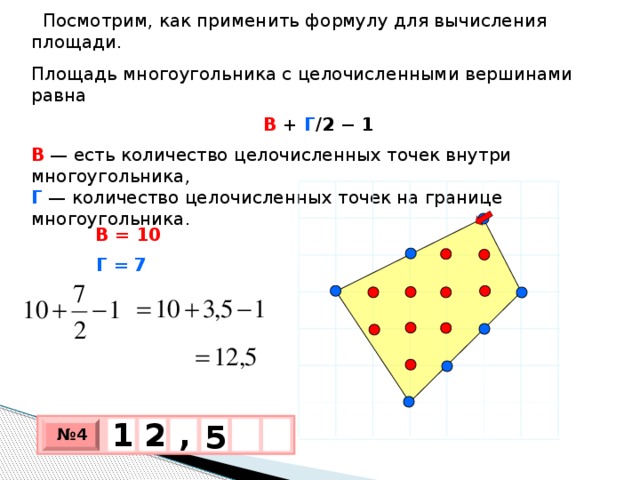
Методическое пособие по вычислению площадей многоугольников в том числе и по формуле Пика
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«ЗАДАНИЯ ДЛЯ САМ.РАБОТЫ(ВЫЧИСЛЕНИЕ ПЛОЩАДИ МНОГОУГОЛЬНИКА НА КЛЕТЧАТОЙ БУМАГЕ С ЦЕЛОЧИСЛЕННЫМИ ВЕРШИНАМИ)»
Просмотр содержимого презентации
«ВЫЧИСЛЕНИЕ ПЛОЩАДИ МНОГОУГОЛЬНИКА НА КЛЕТЧАТОЙ БУМАГЕ С ЦЕЛОЧИСЛЕННЫМИ ВЕРШИНАМИ»
Просмотр содержимого презентации
«Методическое пособие по вычислению площадей многоугольников в том числе и по формуле Пика(Часть 1)»
Просмотр содержимого презентации
«Методическое пособие по вычислению площадей многоугольников в том числе и по формуле Пика(Часть 2)»
Просмотр содержимого презентации
«Методическое пособие по вычислению площадей многоугольников в том числе и по формуле Пика(Часть 3)»
Полезное для учителя
Распродажа видеоуроков!
1570 руб.
2240 руб.
1790 руб.
2560 руб.
1970 руб.
2820 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

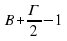
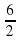
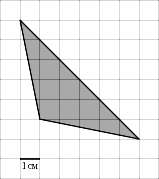
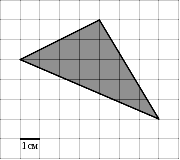

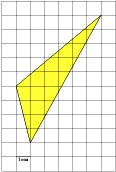
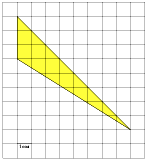
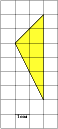
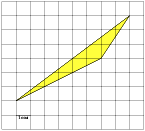

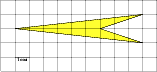

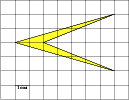
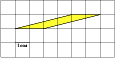


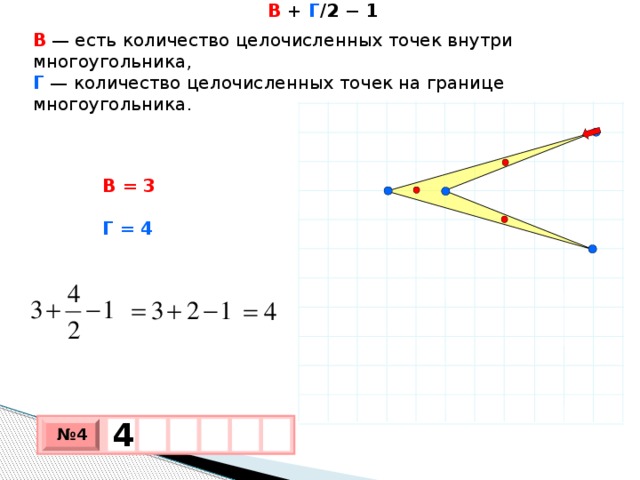
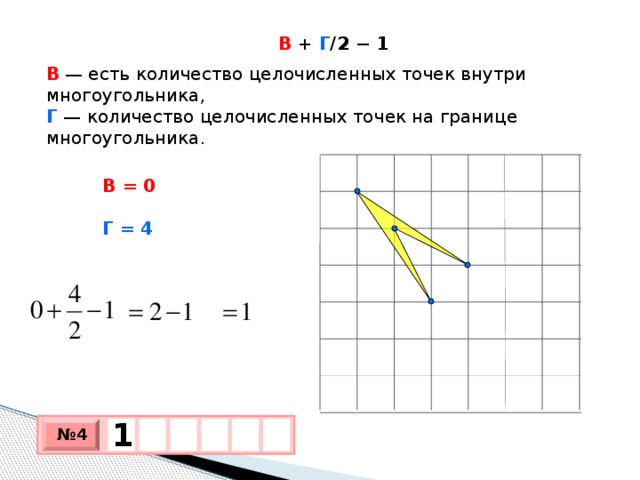


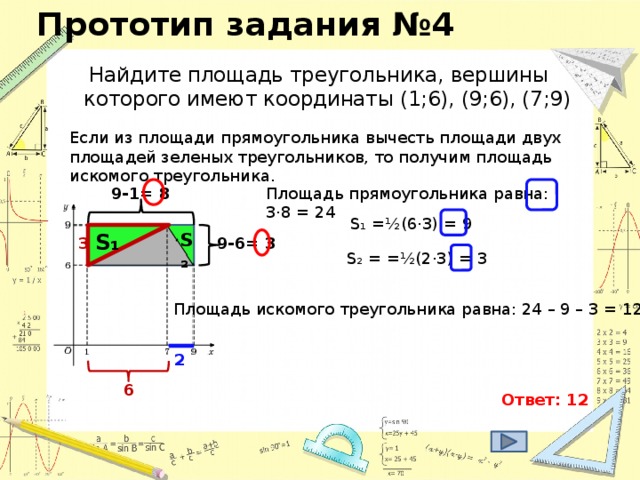
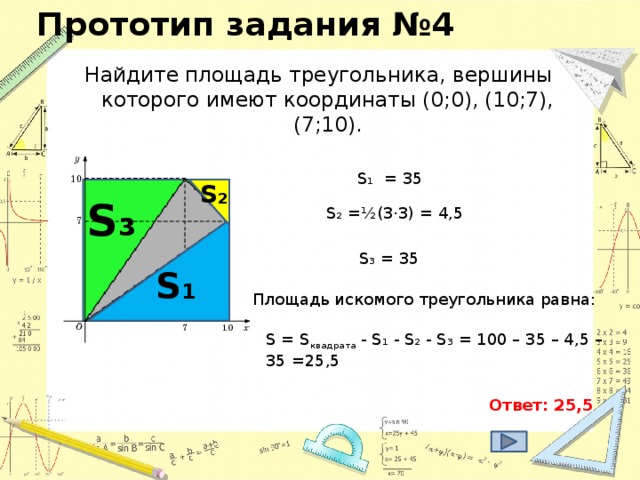
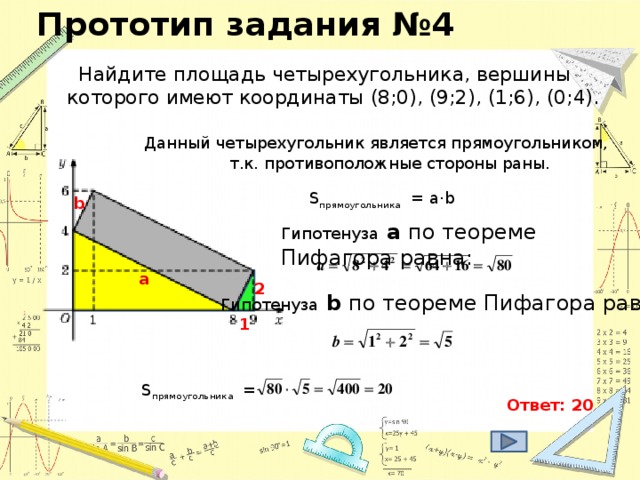
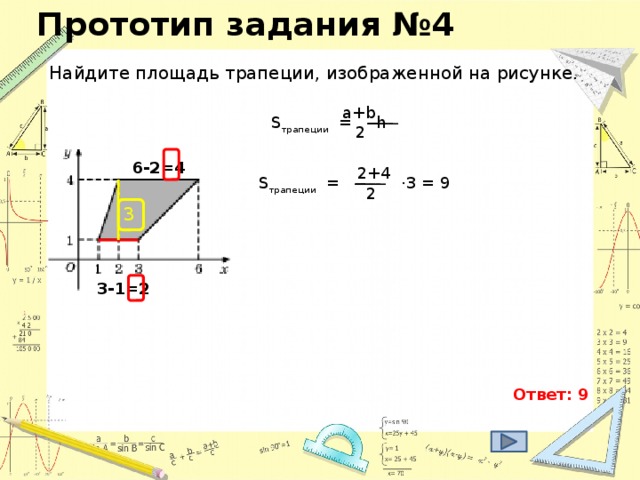
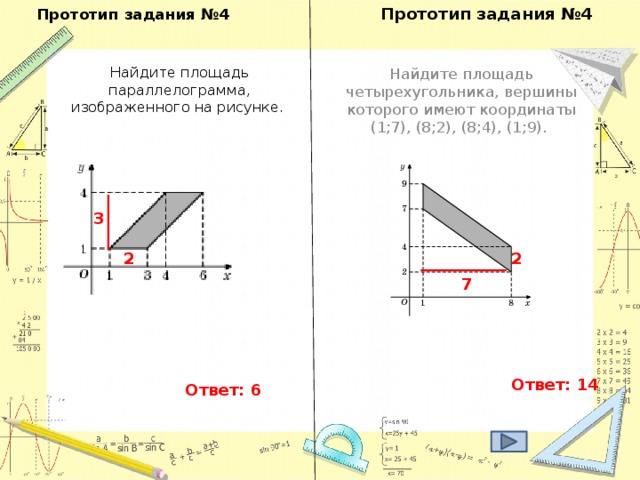
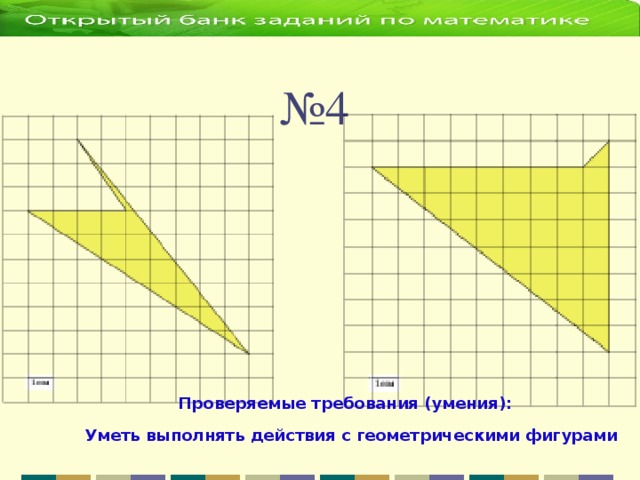
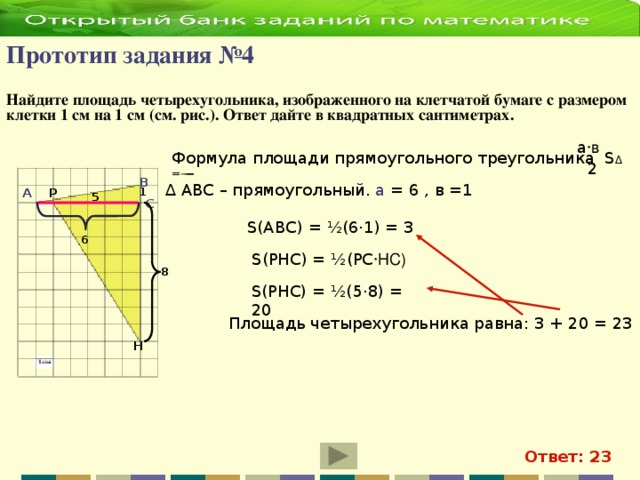



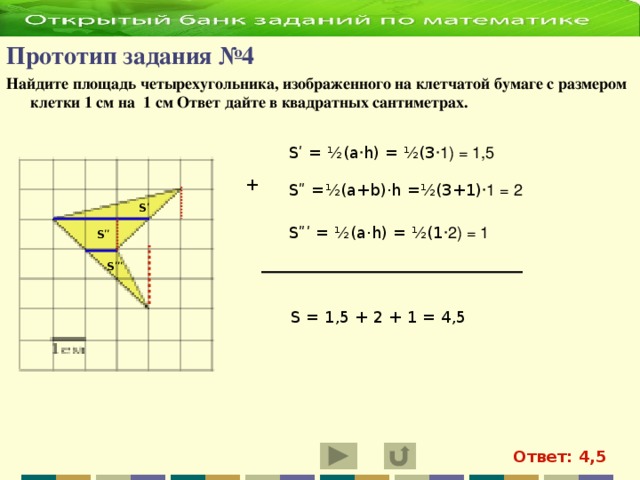
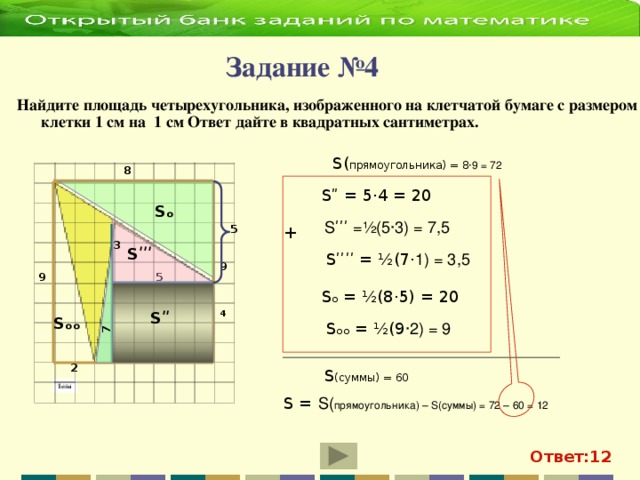

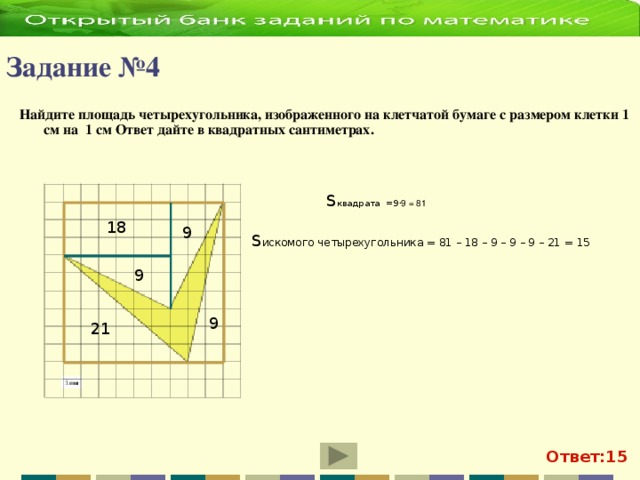


 2 х 2 = 35 2 = х 2 = 612,5 S₃ 392 d у S₁ = х 2 = 612,5 z S₁ х S₂ Из второго прямоугольного треугольника найдем у . 35 z у 21 у 2 + у 2 = 21 2 = 2 у 2 = 21 2 = у 2 = 220,5 S₂ = у 2 = 220,5 S₃ = z 2 z 2 = 392 S₃ = 612,5 – 220,5 = 392; S₃ = S₁ - S₂ ; z 2 + z 2 = d 2 (по теореме Пифагора); 2· z 2 = d 2 d 2 = 2·392 d 2 = 784 d = 28 Ответ: 28" width="640"
2 х 2 = 35 2 = х 2 = 612,5 S₃ 392 d у S₁ = х 2 = 612,5 z S₁ х S₂ Из второго прямоугольного треугольника найдем у . 35 z у 21 у 2 + у 2 = 21 2 = 2 у 2 = 21 2 = у 2 = 220,5 S₂ = у 2 = 220,5 S₃ = z 2 z 2 = 392 S₃ = 612,5 – 220,5 = 392; S₃ = S₁ - S₂ ; z 2 + z 2 = d 2 (по теореме Пифагора); 2· z 2 = d 2 d 2 = 2·392 d 2 = 784 d = 28 Ответ: 28" width="640"


















