Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Математика п?нінен ашы? саба? "Сан аралы?тары"
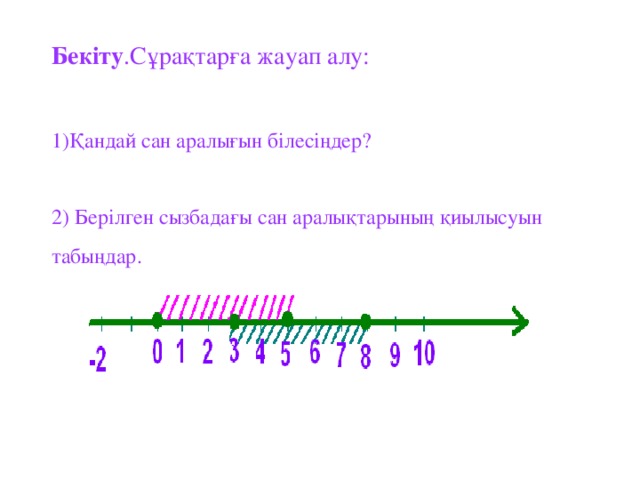
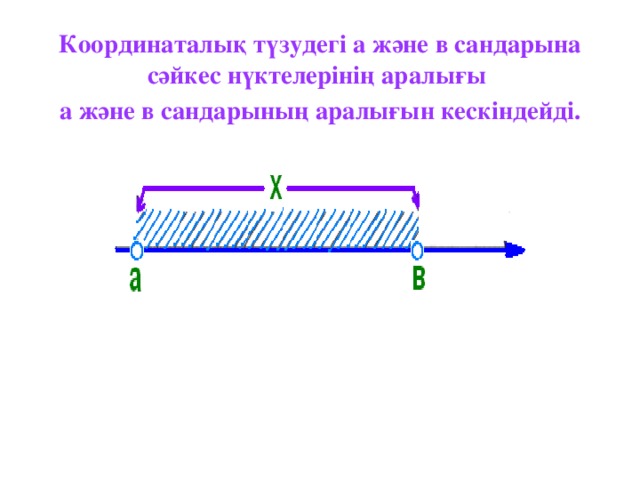
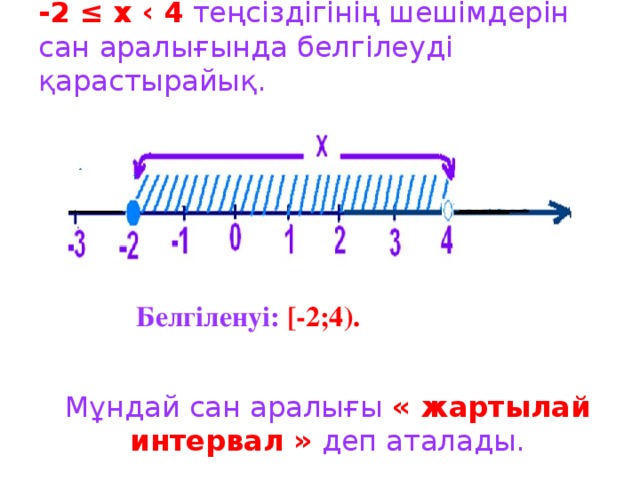
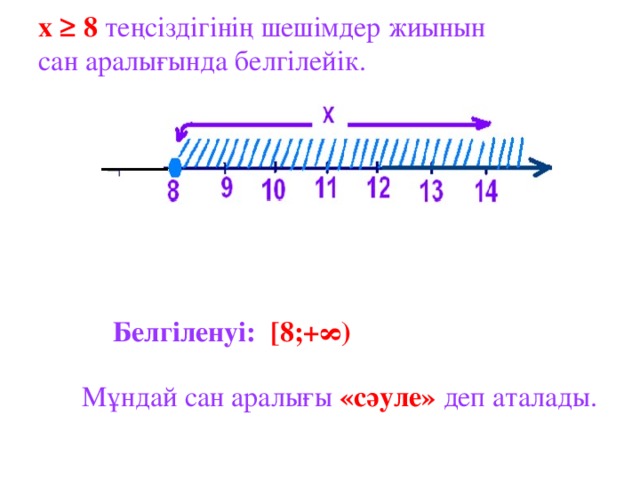
6 сыныпта математика п?нінен "Сан аралы?тары" та?ырыбында ашы? саба? ?тті. ?р т?рлі типтегі ж?мыстар ж?ргізілді, атап айтканда топпен ж?мыс, жеке дара ж?мыс, ?атармен ж?мыс. сергіту с?ті ?ызы?ты ?тті. Сан аралы?тарыны? т?рлерін, те?сіздігіні? шешімдеріні? жиындарын сан аралы?ымен к?рсете білу.
Сан аралы?тарыны? ?иылысуын, бірігуін аны?тай білу. о?ушылар саба?та ?з ойларын т?жырымап айта білді.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Математика п?нінен ашы? саба? "Сан аралы?тары"»
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
2710 руб.
2230 руб.
3190 руб.
1230 руб.
1760 руб.
1970 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


![-4 ≤ х ≤ 3 қатаң емес қос теңсіздігінің шешімдер жиынын сан аралығымен кескіндеуді қарастырайық Белгіленуі: [-4;3] Мұндай сан аралығы “кесінді” деп аталады.](https://fsd.kopilkaurokov.ru/uploads/user_file_568e48349b5a7/img_user_file_568e48349b5a7_4.jpg)

![Екі сан аралығының қиылысуы. [-2;4] аралығы мен [1; 6] аралығының қиылысуы- [1; 4] Белгіленуі: [-2;4] ∩ [1; 6] ═ [1; 4] Сан аралықтарының қиылыспайтын болуы. Мысалы , [-4;1] ∩ [3;7] ═Ø](https://fsd.kopilkaurokov.ru/uploads/user_file_568e48349b5a7/img_user_file_568e48349b5a7_8.jpg)
![Сан аралықтарының бірігуі. Мұндай жағдайда [-2;6] аралығын [-2;3] және [1;6] аралықтарының «бірігуі» деп атайды. Белгіленуі: [-2;3] U [1;6] = [-2;6].](https://fsd.kopilkaurokov.ru/uploads/user_file_568e48349b5a7/img_user_file_568e48349b5a7_9.jpg)
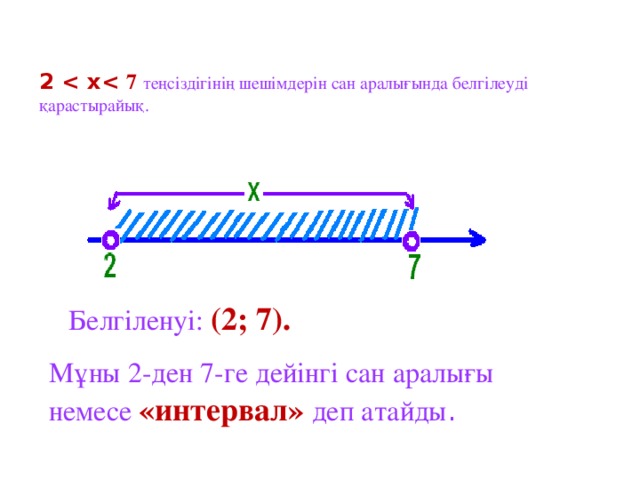
![2 (2; 7) - интервал -4 ≤ х ≤ 3 [-4;3] - кесінді -2 ≤ х ‹ 4 [-2;4) – жартылай интервал х ≥ 8 [8;+∞) - сәуле х ‹ 5 (-∞; 5) - ашық сәуле](https://fsd.kopilkaurokov.ru/uploads/user_file_568e48349b5a7/img_user_file_568e48349b5a7_10.jpg)