8 сынып, алгебра
Саба?ты? ма?саты: Квадратты? те?деуді шешуде формулаларды
тиімді пайдалану да?дыларын ?алыптастыру
Дискриминант ар?ылы квадрат те?деулерді
шешу
Дамытушылы? ма?саты: 1. Ал?ан білімдерін ?рт?рлі жа?дайда
?олдана білуге да?дыландыру.
2. Белсенділігін к?теруге, ойлау
?абілетін арттыру?а, ?з ойын
ж?йелеуге, тез шешім
?абылдау?а ??састы?ты, ?арама-
?айшылы?ты бай?ау?а да?дыландыру.
Т?рбиелік ма?саты: О?ушыларды? білімге деген ?ызы?ушылы?ын
арттыру. ?жым намысын ?ор?ай білетін,
шы?армашылы? ?абілеті дамы?ан т?л?а
т?рбиелеу. Ал?ан білімдеріне
жауапкершілікпен ?арау?а, ?з м?мкіндігіне
сенуге, ?лкен жетістікке ?мтылу?а ?йрету
Саба? т?рі: аралас саба?
Саба? ?дісі: С?ра?- жауап, ауызша жатты?у, есептер шы?ару, ізденіс.
Саба? типі: Білімді бекіту
Саба? барысы:
І. ?йымдастыру кезе?і
1. Т?гендеу.
?рбір бала?а н?тижелік карта ?лестіріледі.Оны бала толтырады.
Аты-ж?ні
Анаграмма
Сергіту
Тест
Теориядан с?ра?
Те?деу шешу
?здік ж?мыс
?орытынды
?пай саны
?пай саны
3
9
6
7
2
27
15-27 ?пай?а дейін «5» ба?а, 9-14 ?пай?а дейін «4» ба?асы ,5-8 дейін «3» ба?асы ?ойылады
І кезе?: «?ызы?ушылы?ты ояту»
1.Анаграмма ( те?деу, коэффициент, т?бір)
- ?еетду
- Фэкоцинетиф
- ?ртіб
2. Ой ?оз?ау . Теориялы? материалды ?айталау:
?рбір жауап?а бір ?пай ?ойылады.
С?ра? – жауап
- 1.?андай те?деуді квадратты? те?деу дейміз?
- 2.Толымсыз квадратты? те?деулер дегеніміз не?
- 3.Келтірілген квадратты? те?деу дегеніміз не?
- 4.Те?деуді? т?бірі дегеніміз не?
- 5.Те?деуді шешу дегеніміз не?
3. Тест «Квадрат те?деуді? т?рлері
Семантикалы? карта
Те?деу
Толымды
Толымсыз
Келтірілген
Келтірілмеген
Толы? балл
x2 + 5x – 3 =0
6x2 + 5 =0
2x2 – 4x =0
5x – 7x2 + 2 =0
2x2 =0
Тексеру
О?ушылар ж?ппен ж?мыс жасайды, бір-біріні? жауаптарын тексереді.
Те?деу
Толымды
Толымсыз
Келтірілген
Келтірілмеген
Толы? балл
x2 + 5x – 3 =0
6x2 + 5 =0
2x2 – 4x =0
5x – 7x2 + 2 =0
2x2 =0
Ба?алау: ?р д?рыс жауап 1 ?паймен ?ойылады.
О?ушылар кілт бойынша бір –бірін тексереді.
ІІ. ( электронды? о?улы? бойынша т?сіндіріледі.
1.Квадратты? те?деуді шешу алгоритмі
2.Дискриминантты? 3 жа?дайы
3. а+в+с, а-в+с ар?ылы те?деу т?бірлерін табу
Егер,а+в+с=0, болса, онда х1=1 х2= с?а
Егер,а-в+с=0, болса, онда х1=-1 х2= - с?а
ІІІ. Жа?а саба?ты бекітуге есептер шы?ару
№128 Квадрат те?деуді? дискриминантын есептеп, ?анша т?бірі болатынын к?рсеті?дер.
1) х2 – 5х – 8 = 0
a = 1, b = – 5, c = – 8
D = b2 – 4ac = (– 5)2 – 4(– 8) = 25+32 = 57>0
екі т?бірі бар.
3) х2 – 14х + 49 = 0
бір т?бірі бар.
5) – 0,5х2 + 6х - 7 = 0
a = – 0.5, b = 6, c = – 7
екі т?бірі бар.
№129 Те?деуді шеші?дер:
1) х2 + 3х + 2 = 0
a = 1, b = 3, c = 2
; ,
3) х2 + 7х + 12 = 0
a = 1, b = – 7 , c = 12
; ,
В де?гейі №134
3) 2х(5х-7) = 2x2 – 7
10x2 – 14x – 2x2 + 7 = 0
8x2 – 14x + 7 = 0
т?бірі жо?.
3) (х – 5)2 = 3х2 – x + 14 = 0
x2 – 10x + 5 – 3x2 + x – 14 = 0
– 2x2 – 9x – 9 = 0
; , ;
2. ?зіндік ж?мыс
Тиімді т?сілмен те?деулерді шеші?дер:
І н?с?а І н?с?а
а) 2х2-5х+3=0 а) х2-2х-3=0
?)5х2-8х+3=0 ?) х2+3х+2=0
Жауаптары: І н?с?а ІІ н?с?а
А)-1;1,5 а)1;-3
?) 1;0,6 ?) -1;-2
ІV. ?орытынды. ?йге тапсырма беру.
Кез-келген квадрат те?деуді шешуге болады. Ол ?шін:
- Жалпы жа?дайда ДИСКРИМИНАНТТЫ табу формуласын, оны? ?ш жа?дайын білуіміз керек.
- Дербес жа?дайларды м??ият ескеру:
- Егер,а+в+с=0, болса, онда х1=1 х2= с?а
- Егер,а-в+с=0, болса, онда х1=-1 х2= - с?а
V. Рефлексия
О?ушыларды? ойларын білу:
-Мен білдім...
-?ызы?тандым...
-?иын болды...
-Мен т?сіндім...
-Мен ?йрендім...
Мен шы?ара алдым...
Мен ?зім шы?арып к?рдім...
Рахмет, сау болы?ыздар!
Просмотр содержимого документа
«саб жосп»
8 сынып, алгебра
Сабақтың мақсаты: Квадраттық теңдеуді шешуде формулаларды
тиімді пайдалану дағдыларын қалыптастыру
Дискриминант арқылы квадрат теңдеулерді
шешу
Дамытушылық мақсаты: 1. Алған білімдерін әртүрлі жағдайда
қолдана білуге дағдыландыру.
2. Белсенділігін көтеруге, ойлау
қабілетін арттыруға, өз ойын
жүйелеуге, тез шешім
қабылдауға ұқсастықты, қарама-
қайшылықты байқауға дағдыландыру.
Тәрбиелік мақсаты: Оқушылардың білімге деген қызығушылығын
арттыру. Ұжым намысын қорғай білетін,
шығармашылық қабілеті дамыған тұлға
тәрбиелеу. Алған білімдеріне
жауапкершілікпен қарауға, өз мүмкіндігіне
сенуге, үлкен жетістікке ұмтылуға үйрету
Сабақ түрі: аралас сабақ
Сабақ әдісі: Сұрақ- жауап, ауызша жаттығу, есептер шығару, ізденіс.
Сабақ типі: Білімді бекіту
Сабақ барысы:
І. Ұйымдастыру кезеңі
1. Түгендеу.
Әрбір балаға нәтижелік карта үлестіріледі.Оны бала толтырады.
| Аты-жөні
| Анаграмма Сергіту | Тест | Теориядан сұрақ | Теңдеу шешу | Өздік жұмыс | Қорытынды |
| Ұпай саны |
|
|
|
|
|
|
| Ұпай саны | 3 | 9 | 6 | 7 | 2 |
27 |
15-27 ұпайға дейін «5» баға, 9-14 ұпайға дейін «4» бағасы ,5-8 дейін «3» бағасы қойылады
І кезең: «Қызығушылықты ояту»
1.Анаграмма ( теңдеу, коэффициент, түбір)
2. Ой қозғау . Теориялық материалды қайталау:
Әрбір жауапқа бір ұпай қойылады.
Сұрақ – жауап
1.Қандай теңдеуді квадраттық теңдеу дейміз?
2.Толымсыз квадраттық теңдеулер дегеніміз не?
3.Келтірілген квадраттық теңдеу дегеніміз не?
4.Теңдеудің түбірі дегеніміз не?
5.Теңдеуді шешу дегеніміз не?
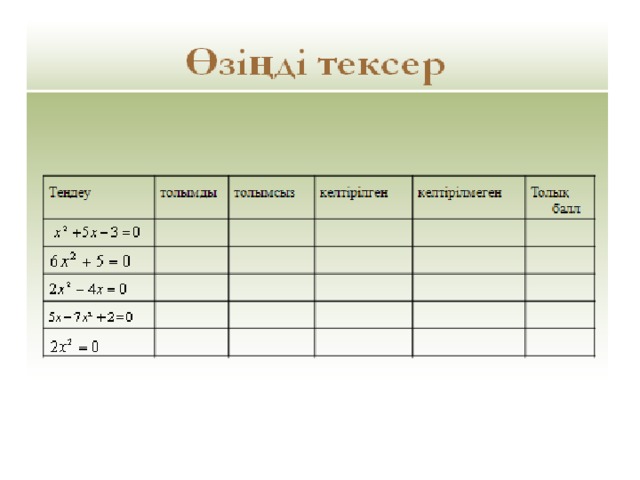
3. Тест «Квадрат теңдеудің түрлері
Семантикалық карта
| Теңдеу | Толымды | Толымсыз | Келтірілген | Келтірілмеген | Толық балл |
| x2 + 5x – 3 =0 |
|
|
|
|
|
| 6x2 + 5 =0 |
|
|
|
|
|
| 2x2 – 4x =0 |
|
|
|
|
|
| 5x – 7x2 + 2 =0 |
|
|
|
|
|
| 2x2 =0 |
|
|
|
|
|
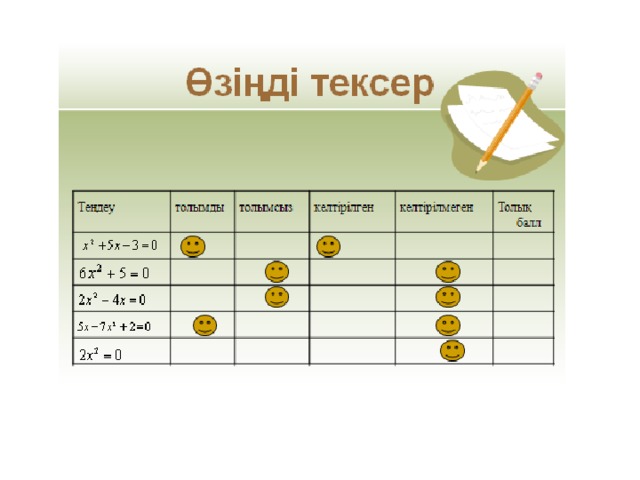
Тексеру
Оқушылар жұппен жұмыс жасайды, бір-бірінің жауаптарын тексереді.
| Теңдеу | Толымды | Толымсыз | Келтірілген | Келтірілмеген | Толық балл
|
| x2 + 5x – 3 =0 | 
|
|
|
|
|
| 6x2 + 5 =0 |
|
|
|
|
|
| 2x2 – 4x =0 |
|
|
|
|
|
| 5x – 7x2 + 2 =0 |
|
|
|
|
|
| 2x2 =0 |
|
|
|
|
|
Бағалау: Әр дұрыс жауап 1 ұпаймен қойылады.
Оқушылар кілт бойынша бір –бірін тексереді.
ІІ. Жаңа тақырып түсіндіру ( электрондық оқулық бойынша түсіндіріледі.
1.Квадраттық теңдеуді шешу алгоритмі
2.Дискриминанттың 3 жағдайы
3. а+в+с, а-в+с арқылы теңдеу түбірлерін табу
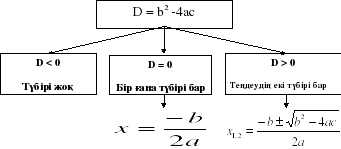
Егер,а+в+с=0, болса, онда х1=1 х2= с∕а
Егер,а-в+с=0, болса, онда х1=-1 х2= - с∕а
ІІІ. Жаңа сабақты бекітуге есептер шығару
№128 Квадрат теңдеудің дискриминантын есептеп, қанша түбірі болатынын көрсетіңдер.
1) х2 – 5х – 8 = 0
a = 1, b = – 5, c = – 8
D = b2 – 4ac = (– 5)2 – 4(– 8) = 25+32 = 570
екі түбірі бар.
3) х2 – 14х + 49 = 0
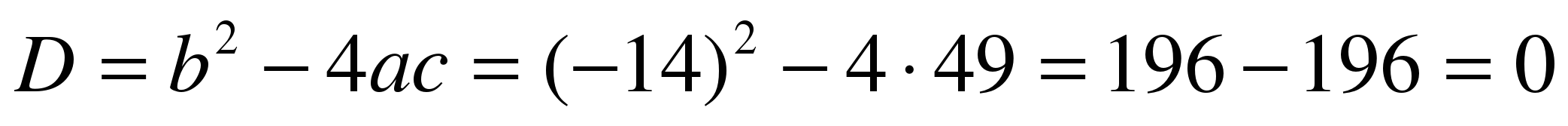
бір түбірі бар.
5) – 0,5х2 + 6х - 7 = 0
a = – 0.5, b = 6, c = – 7
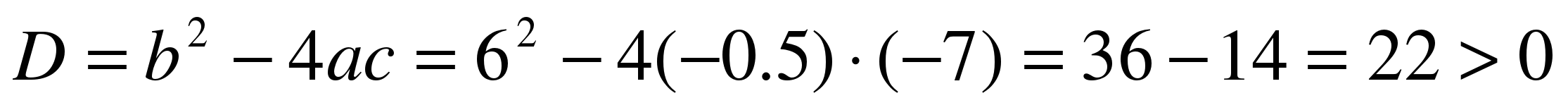
екі түбірі бар.
№129 Теңдеуді шешіңдер:
1) х2 + 3х + 2 = 0
a = 1, b = 3, c = 2
; 
, 
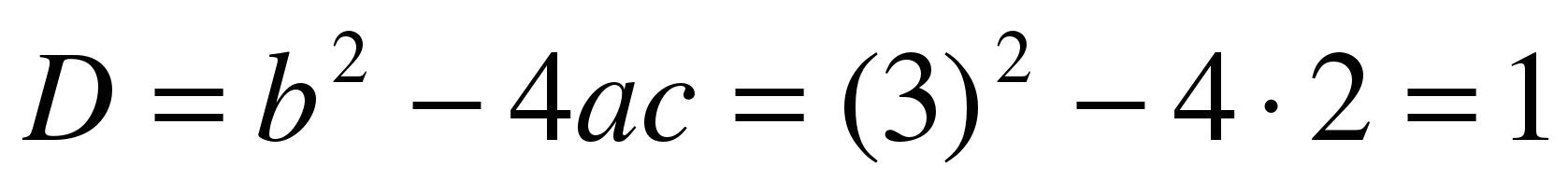
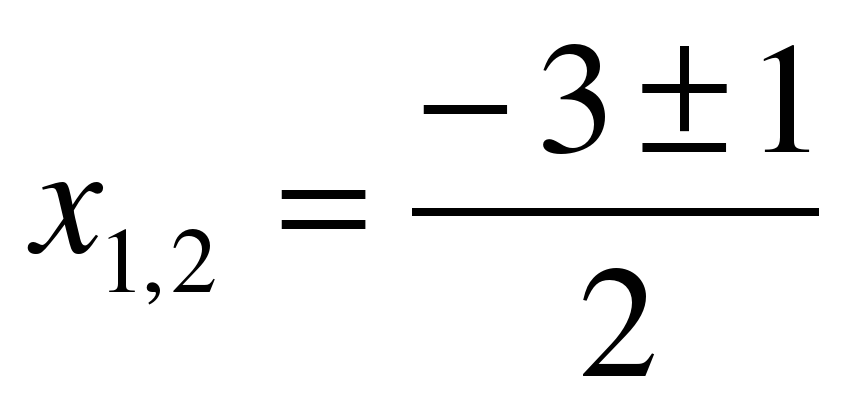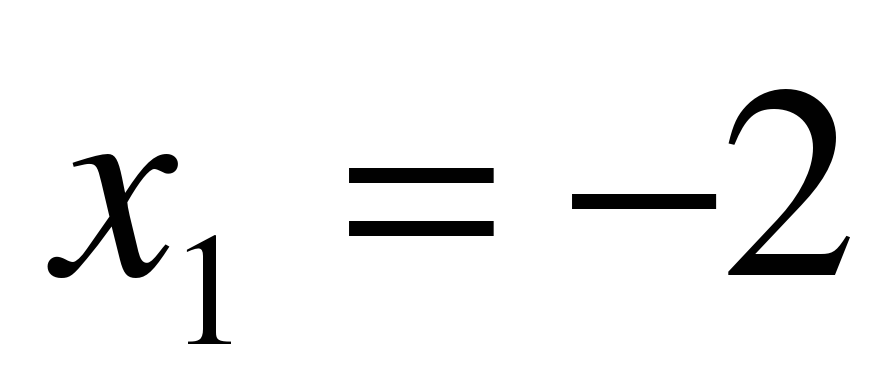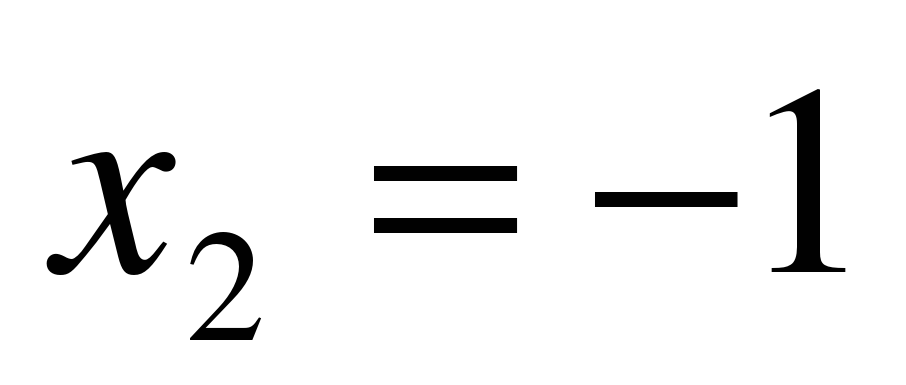
3) х2 + 7х + 12 = 0
a = 1, b = – 7 , c = 12
; 
, 
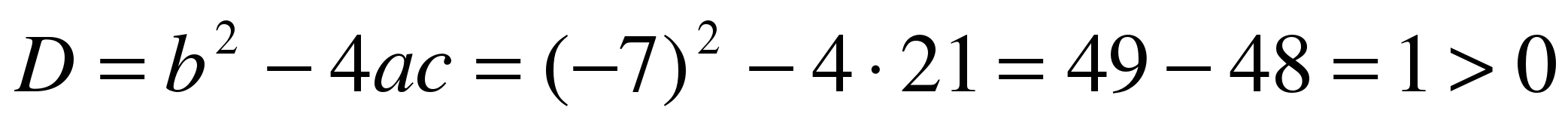
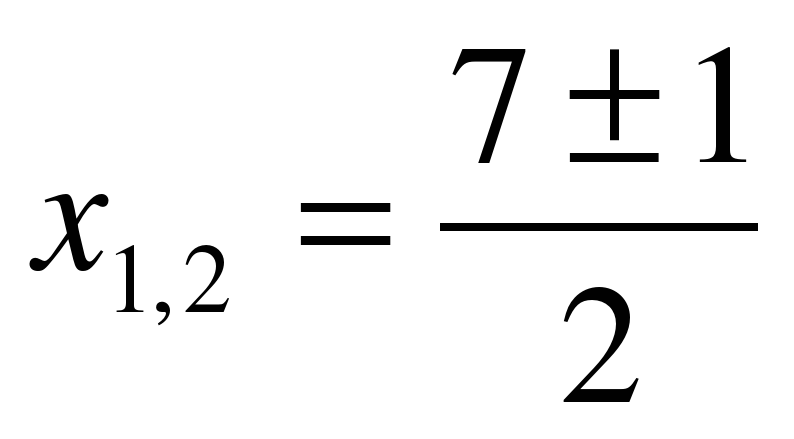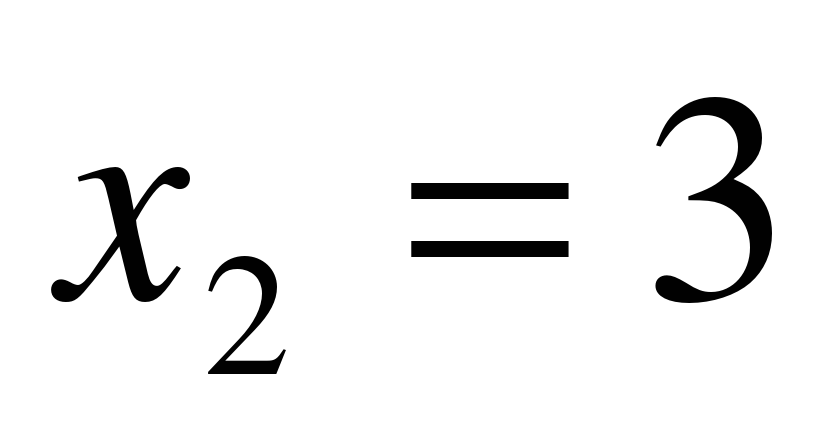
В деңгейі №134
3) 2х(5х-7) = 2x2 – 7
10x2 – 14x – 2x2 + 7 = 0
8x2 – 14x + 7 = 0
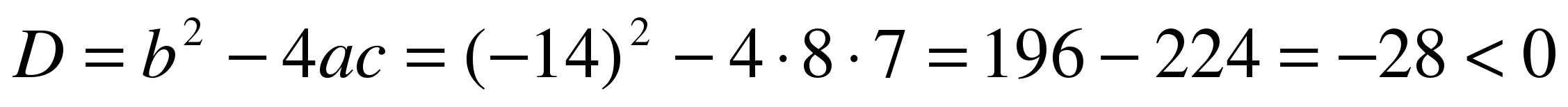
түбірі жоқ.
3) (х – 5)2 = 3х2 – x + 14 = 0
x2 – 10x + 5 – 3x2 + x – 14 = 0
– 2x2 – 9x – 9 = 0
; 
, 
;
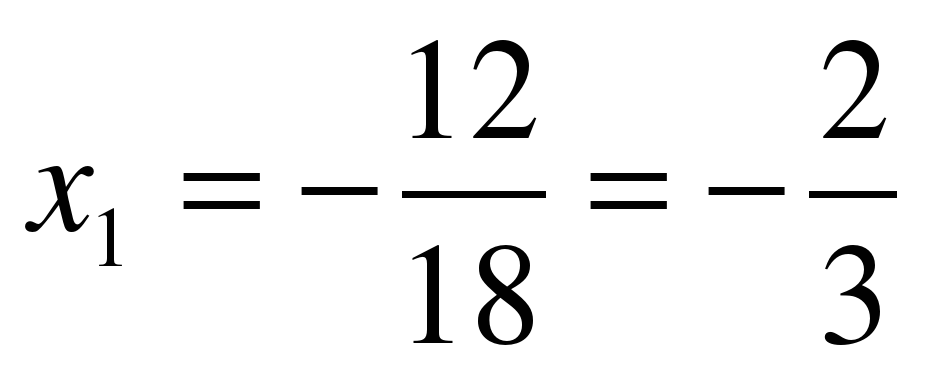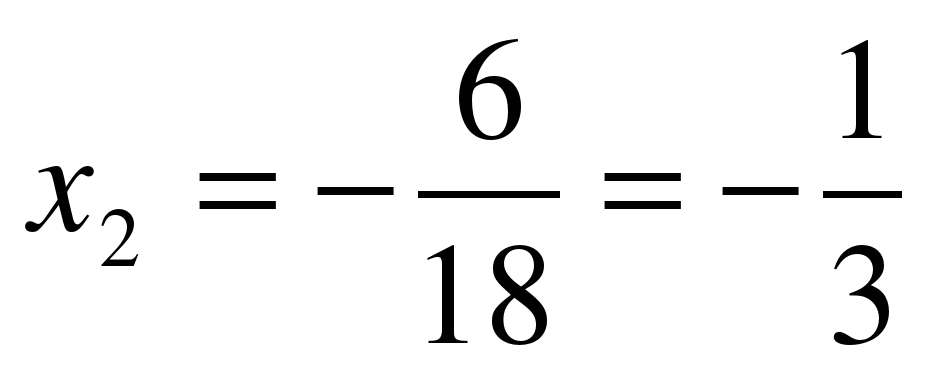2. Өзіндік жұмыс
Тиімді тәсілмен теңдеулерді шешіңдер:
І нұсқа І нұсқа
а) 2х2-5х+3=0 а) х2-2х-3=0
ә)5х2-8х+3=0 ә) х2+3х+2=0
Жауаптары: І нұсқа ІІ нұсқа
А)-1;1,5 а)1;-3
Ә) 1;0,6 ә) -1;-2
ІV. Қорытынды. Үйге тапсырма беру.
Кез-келген квадрат теңдеуді шешуге болады. Ол үшін:
Жалпы жағдайда ДИСКРИМИНАНТТЫ табу формуласын, оның үш жағдайын білуіміз керек.
Дербес жағдайларды мұқият ескеру:
Егер,а+в+с=0, болса, онда х1=1 х2= с∕а
Егер,а-в+с=0, болса, онда х1=-1 х2= - с∕а
V. Рефлексия
Оқушылардың ойларын білу:
-Мен білдім...
-Қызықтандым...
-Қиын болды...
-Мен түсіндім...
-Мен үйрендім...
Мен шығара алдым...
Мен өзім шығарып көрдім...
Рахмет, сау болыңыздар!
Келісемін__________ Бекітемін_____________
АҚБҮО-ның әдіскері №3 орта мектеп директоры
Жаңғалиева Н. Ғ Утесинов М.Ж
Тақырыбы: Квадрат теңдеу
түбірлерінің формуласы
№3 орта мектептің математика пәні мұғалімі
Кайрханова Айгүл Сейсенайқызы
Ақтау-2011
Просмотр содержимого презентации
«Презентация Microsoft PowerPoint»
« Ақтау қаласы №3 орта мектебі» мемлекеттік мекемесі .
Математика пәнінің мұғалімі
Кайрханова Айгүл
Сейсенайқызы
Оқушы білімін тексеру .
Аты-жөні
Анаграмма
Сергіту
Ұпай саны
Тест
Теориядан сұрақ
Теңдеу шешу
Өздік жұмыс
Қорытынды
Бағалау шектері:
15 – 20 ұпай – “5”. 9 – 14 ұпай – “4”. 5 - 8 ұпай – “3”.
Анаграмма
- Мына сөздерден математикалық термин құрастыр:
- Ңеетду
- Фэкоцинетиф
- Үрті б
СҰРАҚ-ЖАУАП
a х 2 - b х+ c =0 түріндегі теңдеу квадрат теңдеу деп аталады, мұндағы х – айнымалы, а, b және с – кез келген сандар және a≠0; а, в және с – сандары квадрат теңдеудің коэффициенттері
b немесе с, немесе b мен с нөлге тең
болатын дербес жағдайдағы квадраттық
теңдеу толымсыз квадрат теңдеу деп
аталады.
Егер толық квадрат теңдеудегі бірінші коэффициент 1 – ге тең ( a=1 ) болса,
онда келтірілген квадрат теңдеу деп аталады.
Квадрат теңдеуді дұрыс теңдікке
айналдыратын айнымалының мәні
теңдеудің түбірі деп аталады.
Квадрат теңдеуді шешу дегеніміз – оның барлық түбірлерін табу немесе түбірлері жоқ екенін көрсету.
28.10.2011
Сабақтың тақырыбы:
Квадрат теңдеу түбірлерінің формуласы
Квадрат теңдеулерді шешуде формулаларды тиімді пайдалану дағдыларын қалыптастыру,дискриминант арқылы квадрат теңдеулерді шешу
Алған білімдерін әр түрлі жағдайларда қолдана білуге дағдыландыру.Белсендігін көтеруге , ойлау қабілетін арттыруға , өз ойын жүйелеуге , тез шешім қабылдауға ұқсастықты , қарама-қайшылықты байқауғадағдыландыру
Оқушылардың білімге деген қызығушылығын арттыру. Ұжым намысын қорғай білетін, шығармашылық қабілеті дамыған тұлға тәрбиелеу. Алған білімдеріне жауапкершілікпен қарауға, өз мүмкіндігіне сенуге ,үлкен жетістікке ұмтылуға үйрету
ax 2 + bx + c =0
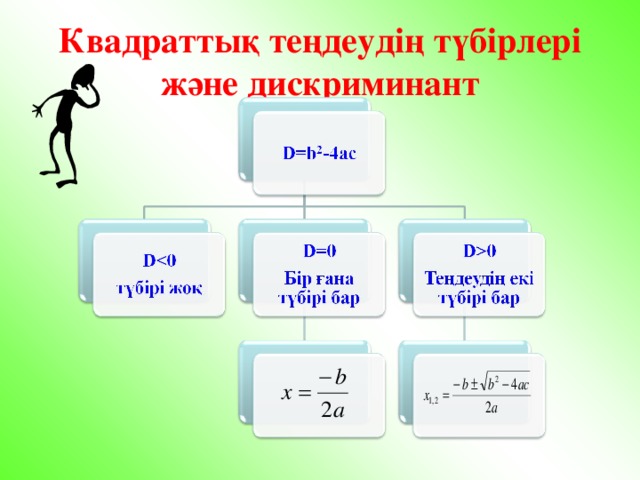
Квадраттық теңдеудің түбірлері және дискриминант
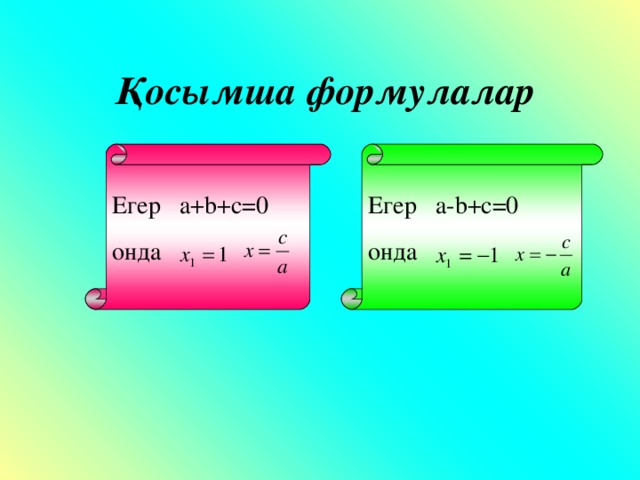
Қосымша формулалар
Егер а- b+c=0
онда
Егер а+ b+c=0
онда
Теңдеуді шешіңіздер:
- 2х 2 +3х-5=0
- 25х 2 -10х+1=0
- 9х 2 -3х+2=0
- 5х 2 -2х-7=0
а-в+с=0 5-(-2)+(-7)=0
Жұмыс дәптеріне есептер шығару
№ 129
№ 134
№ 12 8
А деңгей №128 Квадрат теңдеудің дискриминантын есептеу, қанша түбірі болатынын көрсетіңдер.
3) х 2 – 14х + 49 = 0
Егер квадрат теңдеу толық болса, түрінде болса, онда дискриминант табу арқылы шешеміз:
1.
2.
3.
(шешімі жоқ)
а+ b+c=0 болса, онда
4.
5.
а -c+b=0 болса, онда
В деңгей №134 Теңдеуді шешіңдер.
1 ) 2х(5х-7) = 2x 2 – 5
1-нұсқа
Теңдеу
Коэффициенттерді
қосындысы
а + в + с
Түбірлер
а+ в +с=0
2-нұсқа
Теңдеу
а - в + с
Түбірлері
а-в+с =0
1-нұсқа
Теңдеу
Коэффициенттердің
қосындысы
а + в + с
Түбірлер
2 – 5 + 3 = 0
5 – 8 + 3 = 0
а + в + с = 0
2-нұсқа
Теңдеу
а - в + с
1 – (- 2) +(- 3) = 0
Түбірлері
1 – 3 + 2 = 0
а - в + с = 0
Аты-жөні
Анаграмма
Сергіту
Ұпай саны
Тест
Теориядан сұрақ
Теңдеу шешу
Өздік жұмыс
Қорытынды
Бағалау шектері:
15 – 20 ұпай – “5”. 9 – 14 ұпай – “4”. 5 - 8 ұпай – “3”.
V. Оқушылар білімін бағалау
V І . Үй тапсырмасы:
- “ Квадрат теңдеуді шешу формулалары” тақырыбын оқу
2.
Жұмыс дәптеріне
№ 130(1,2), 135(1)есептер
0. D=0. D ; 2) Келт ірілген квадрат теңдеу болғанда, оны Виет теремасы арқылы шешу; 3) Дербес жағдайларды мұқият ескеру: a+b+c=0 болғанда , a-c+b=0 болғанда, Үйге тапсырма: № 130 –№135 есептер." width="640"
Қорытындылау:
Кез келген квадрат теңдеуді шешуге болады.
Ол үшін:
- Жалпы жағдайда ДИСКРМИНАНТТЫ табу формуласын біліуіміз қажет, оның үш жағдайын.
D0. D=0. D ;
2) Келт ірілген квадрат теңдеу болғанда, оны Виет теремасы арқылы шешу;
3) Дербес жағдайларды мұқият ескеру:
a+b+c=0 болғанда ,
a-c+b=0 болғанда,
Үйге тапсырма: № 130 –№135 есептер.
- Мен білдім…
- Қызықтандым…
- Қиын болды …
- Мен түсіндім…
- Мен үйрендім…
- Мен шығара алдым…
- Мен өзім шығарып көрдім…
Шығамын десең биік шыңның басына,
Адал досың – Біліміңді ал қасыңа.
Зула, топ жар! Бәйгеге түс, бекем бол,
Тула, толқы, тебірен бірақ тасыма!
