
Исследовательская деятельность как метод воспитания креативной личности.

Цель проведения: познакомить учителей с методическими приёмами организации исследовательской работы по решению задач на построение.

«Учитель не должен забывать, что ученье, лишённое всякого интереса и взятое только силой принуждения, убивает в ученике охоту к ученью, без которой он далеко не уйдёт»- слова, сказанные выдающимся русским педагогом К. Д. Ушинским,говорят о важности проблемы.


- Одной из психолого- педагогических концепций учения является теория проблемного обучения М.И. Махмутова. В основу этой теории положены частично-поисковый и поисково-исследовательский методы работы, которым я отвожу первостепенное значение. Новизна опыта заключается в создании системного подхода в развитии творческих способностей учащихся на уроках математики путем использования технологии проблемного обучения.

- Для определения уровней творческой самореализации учащихся использовался пакет методик:
- а) Методика Е. Торренса для определения творческой активности («беглость») и творческого мышления («гибкость»)
- б) Методика диагностики уровня творческой активности учащихся М.И. Рожкова и др.
- Эффективность исследовательской деятельности зависит и от меры увлеченности ученика, и от умения ее выполнять.

Задачи на построение


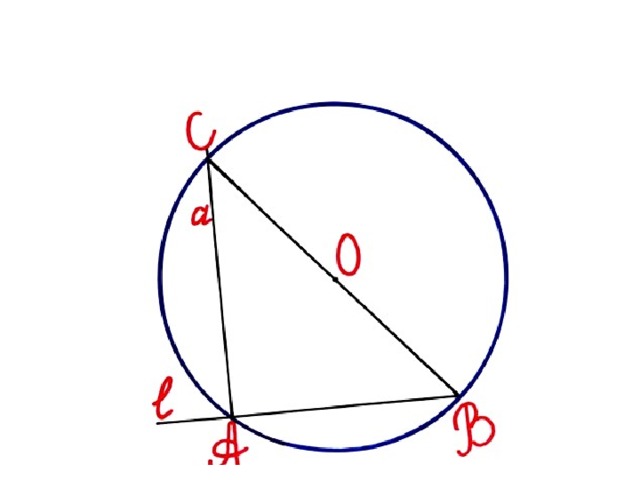


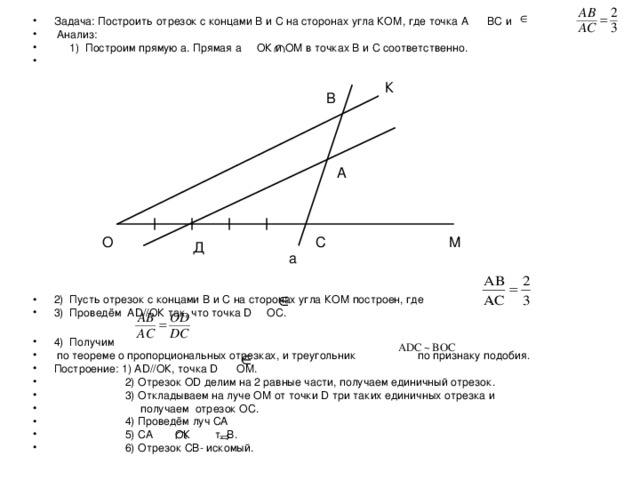
- Задача: Построить отрезок с концами В и С на сторонах угла КОМ, где точка А ВС и
- Анализ:
- 1) Построим прямую а. Прямая а ОК и ОМ в точках В и С соответственно.
- 2) Пусть отрезок с концами В и С на сторонах угла КОМ построен, где .
- 3) Проведём А D //ОК так, что точка D OC .
- 4) Получим
- по теореме о пропорциональных отрезках, и треугольник по признаку подобия.
- Построение: 1) А D //ОК, точка D OM.
- 2) Отрезок О D делим на 2 равные части, получаем единичный отрезок.
- 3) Откладываем на луче ОМ от точки D три таких единичных отрезка и
- получаем отрезок ОС.
- 4) Проведём луч СА
- 5) СА ОК т. В.
- 6) Отрезок СВ- искомый.
К
В
А
О
М
С
Д
а

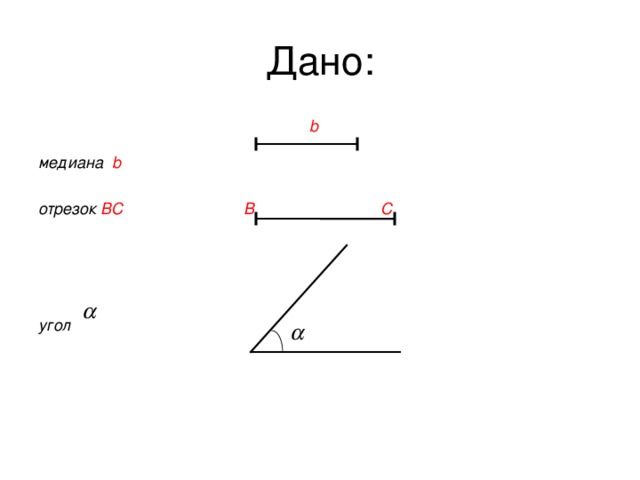
b
медиана b
отрезок ВС В С
угол
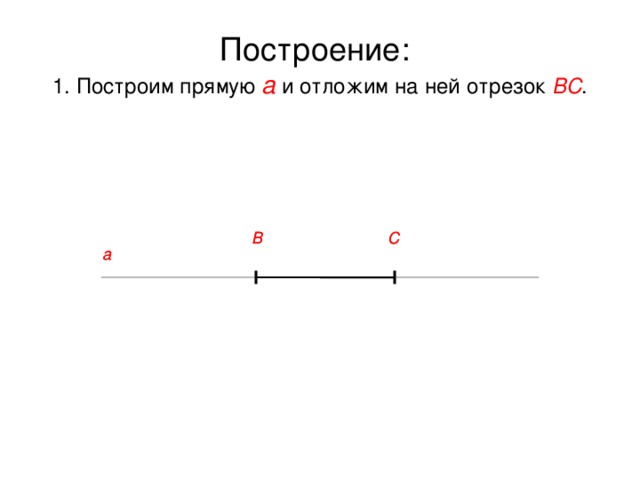
Построение: 1. Построим прямую а и отложим на ней отрезок ВС .
В С
В С
а
а
 т . S . В С а S" width="640"
т . S . В С а S" width="640"
•
2.Найдём середину отрезка ВС = т . S .
В С
а
S
•
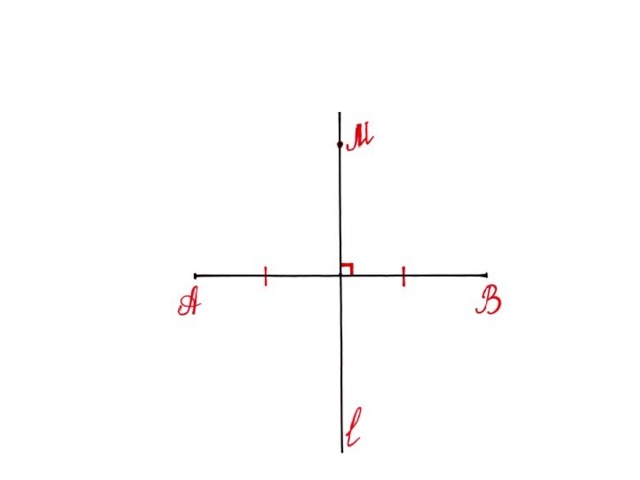
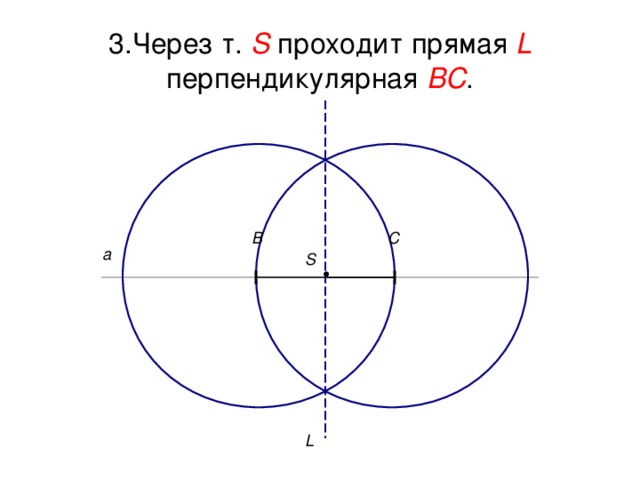
3.Через т. S проходит прямая L перпендикулярная ВС .
В С
а
S
L
•
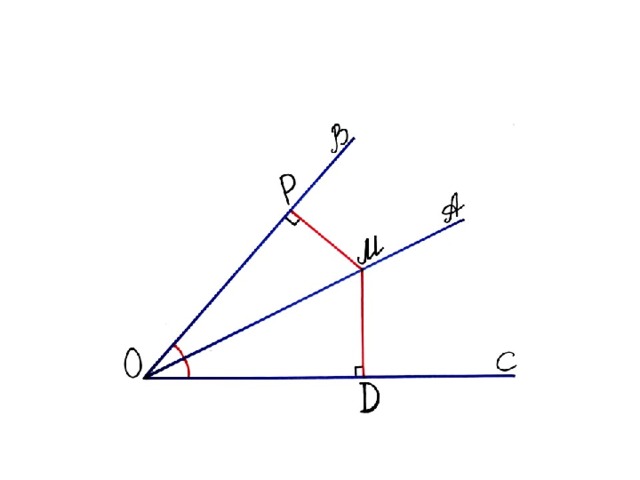
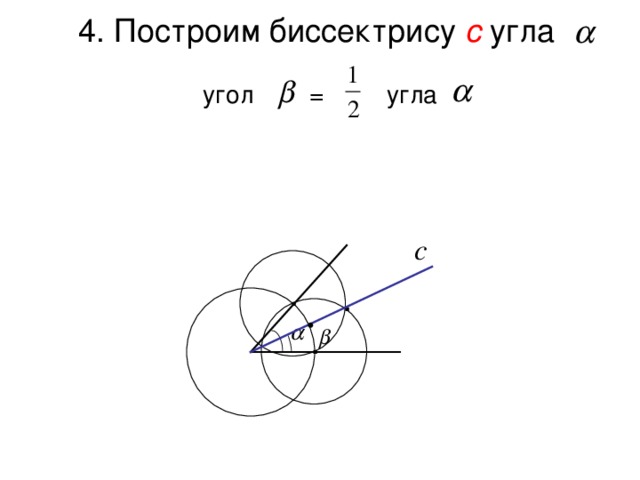
4. Построим биссектрису c угла угол = угла
.
.
.
•
•
•
•
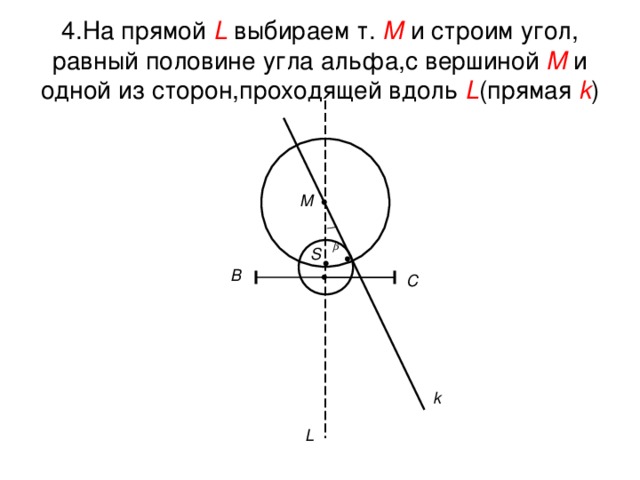
4.На прямой L выбираем т. М и строим угол, равный половине угла альфа,с вершиной М и одной из сторон,проходящей вдоль L (прямая k )
М
S
В
С
k
L
•
•
•
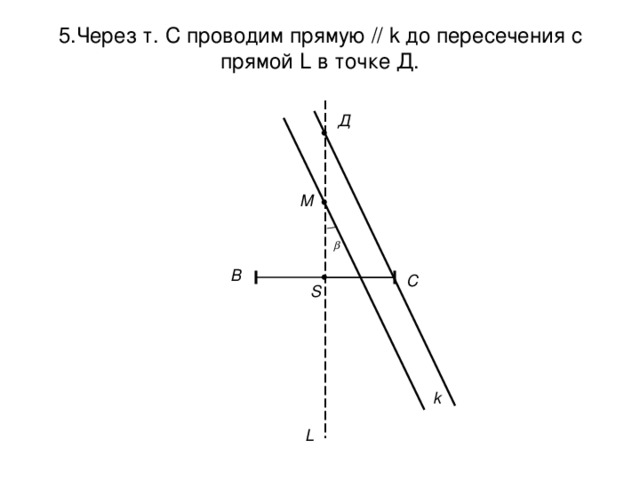
5 .Через т. С проводим прямую // k до пересечения с прямой L в точке Д.
Д
М
В
С
S
k
L
 т.О Д О В С S L" width="640"
т.О Д О В С S L" width="640"
•
•
•
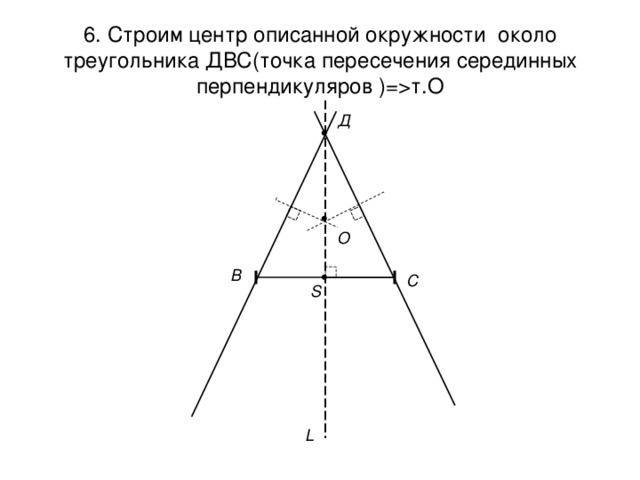
6. Строим центр описанной окружности около треугольника ДВС(точка пересечения серединных перпендикуляров )= т.О
Д
О
В
С
S
L
•
•
•
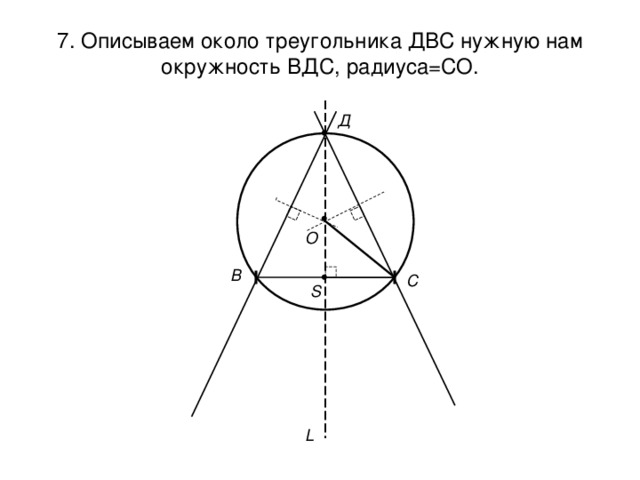
7. Описываем около треугольника ДВС нужную нам окружность ВДС, радиуса=СО.
Д
О
В
С
S
L
•
•
•
•
•
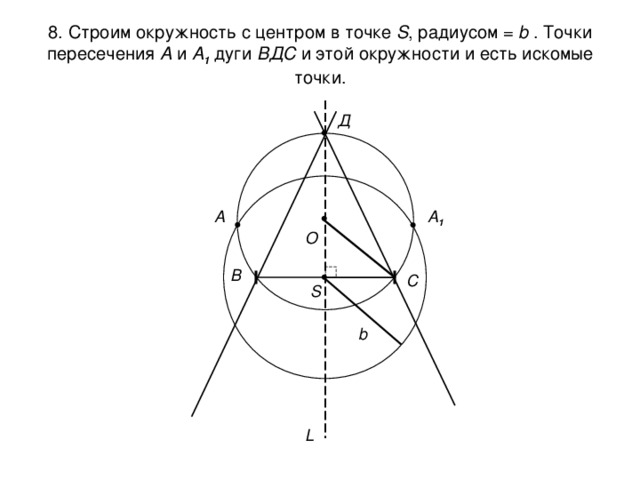
8. Строим окружность с центром в точке S , радиусом = b . Точки пересечения А и А 1 дуги ВДС и этой окружности и есть искомые точки.
Д
А
А 1
О
В
С
S
b
L
•
•
•
•
•
•
•
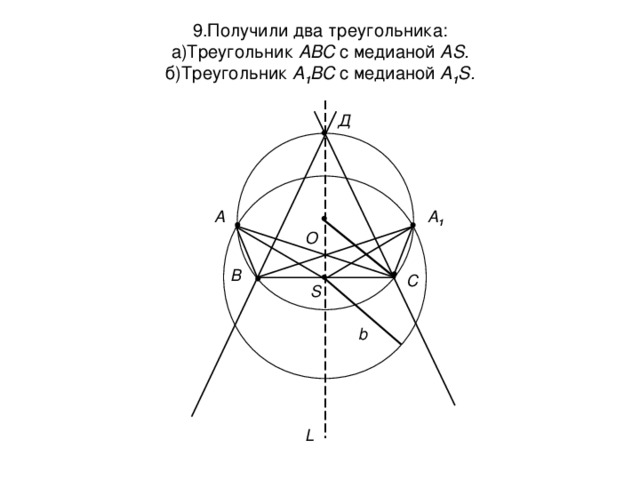
9.Получили два треугольника: а)Треугольник АВС с медианой А S . б)Треугольник А 1 ВС с медианой А 1 S .
Д
А
А 1
О
В
С
S
b
L

Построение правильного пятиугольника
"Геометрия обладает двумя великими
сокровищами. Первое - это теорема Пифагора,
второе - деления отрезка в крайнем и среднем
отношении"
Иоганн Кеплер

Правильные многоугольники привлекали внимание древнегреческих учёных
ещё задолго да Архимеда. Пифагорейцы, выбравшие эмблемой своего союза
пентаграмму - пятиконечную звезду, придавали очень большое значение
задаче о делении окружности на равные части, то есть о построении
правильного вписанного многоугольника.
Альбрехт Дюрер (1471-1527гг),
ставший олицетворением Возрождения в Германии
приводит теоретически точный способ построения
правильного пятиугольника, заимствованный из великого
сочинения Птолемея "Альмагест". Интерес Дюрера к
построению правильных многоугольников отражает
использование их в Средние века в арабских и готических
орнаментах, а после изобретения огнестрельного оружия
- в планировке крепостей

Дюрер пишет: «Необходимо, чтобы тот, кто что-либо умеет, обучил этому
других, которые в этом нуждаются. Это я и вознамерился сделать».
Живописец подробно разрабатывает теорию
пропорций человеческого тела. Важное место в своей системе соотношений
Дюрер отводил золотому сечению. Рост человека делится в золотых
пропорциях линией пояса, а также линией, проведенной через кончики средних
пальцев опущенных рук, нижняя часть лица – ртом и т.д.
Известен пропорциональный циркуль Дюрера.

Леонардо да Винчи также много писал о многоугольниках, но именно
Дюрер, а не Леонардо, передал средневековые способы построения
потомкам. Дюрер, конечно, был знаком с " Началами" Евклида, но не привел
в своем "Руководстве к измерению" (о построениях при помощи циркуля и
линейки) предложенный Евклидом теоретически точный способ построения
правильного пятиугольника.

Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении , названное впоследствии золотым сечением и привлекавшим к себе внимание художников и архитекторов на протяжении нескольких столетий.

Способ построения пятиугольника
по Дюреру
Приближенное построение правильного пятиугольника представляет собой интерес. А.Дюрером оно проводится при условии неизменности раствора циркуля, что повышает точность построения. Способ построения описан Дюрером так:
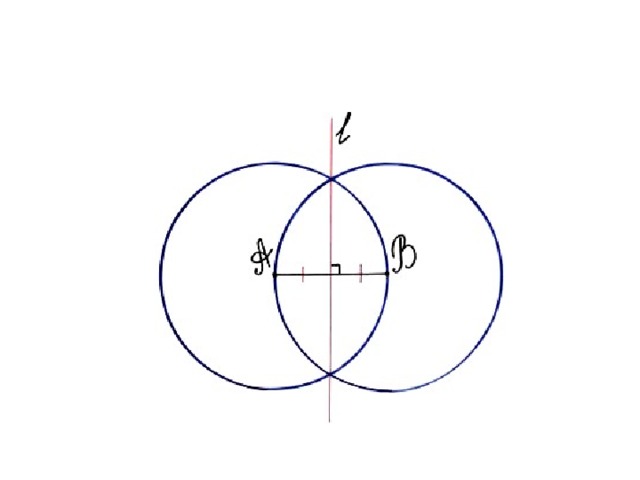
" Однако пятиугольник, построенный неизменным раствором циркуля, делай так. Проведи две окружности так, чтобы каждая из них проходила через центр другой. Два центра А и В соедини прямой линией. Это и будет стороной пятиугольника. Точки пересечения окружностей обозначь сверху С, снизу D и проведи прямую линию CD. После этого возьми циркуль с неизменным раствором и, установив одну его ножку в точку D, другой проведи через оба центра А и В дугу до пересечения её с обеими окружностями. Точки пересечения обозначь через E и F, а точку пересечения с прямой CD обозначь буквой G. Теперь проведи прямую линию через Е и G до пересечения с линией окружности. Эту точку обозначь Н. Затем проведи другую линию через F и G до пересечения с линией окружности и поставь здесь J. Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник."
Построение по Дюреру
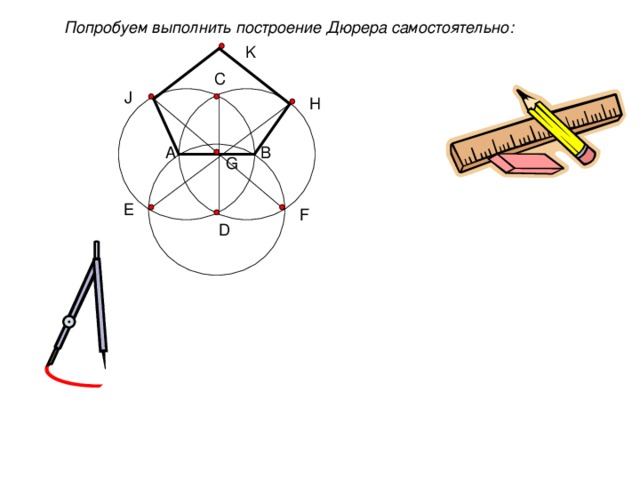
Попробуем выполнить построение Дюрера самостоятельно:
K
C
J
H
B
A
G
E
F
D
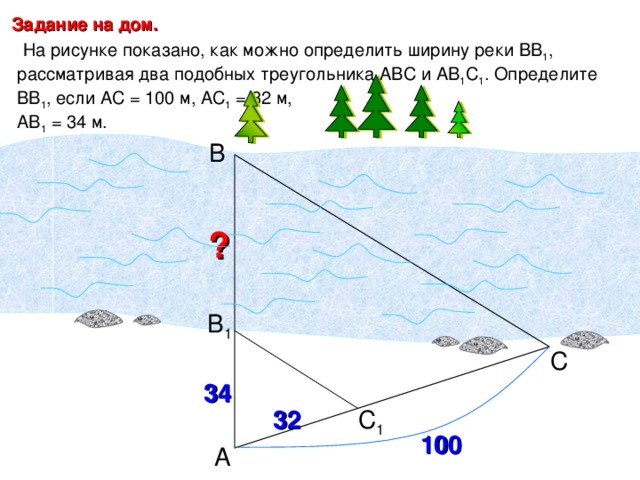
Задание на дом.
На рисунке показано, как можно определить ширину реки ВВ 1 , рассматривая два подобных треугольника АВС и АВ 1 С 1 . Определите ВВ 1 , если АС = 100 м, АС 1 = 32 м,
АВ 1 = 34 м.
В
?
В 1
С
34
С 1
3 2
100
А



















 т . S . В С а S" width="640"
т . S . В С а S" width="640"




 т.О Д О В С S L" width="640"
т.О Д О В С S L" width="640"



























