Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Білімділік:О?ушыларды? квадрат ?шм?ше ж?не оны к?бейткіштерге жіктеу, квадратты? те?деуге келтірілетін те?деулерді? кейбір т?рлерін шеше білу да?дыларын жетілдіру.
Дамытушылы?:Жылдам ой ?орыту, тап?ырлы?, тияна?тылы? ?асиеттерін дамыту. О?у материалын ?за? есте са?тау ?абілетін дамыту.
Т?рбиелік:О?ушыларды ?йымшылды??а, ??ыптылы??а, д?лдікке т?рбиелеу, ?з біліміне жауапкершілікпен ?арау?а да?дыландыру.
Мақсаты :
Білімділік :Оқушылардың квадрат үшмүше және оны көбейткіштерге жіктеу, квадраттық теңдеуге келтірілетін теңдеулердің кейбір түрлерін шеше білу дағдыларын жетілдіру.
Дамытушылық : Жылдам ой қорыту, тапқырлық, тиянақтылық қасиеттерін дамыту. Оқу материалын ұзақ есте сақтау қабілетін дамыту.
Тәрбиелік: Оқушыларды ұйымшылдыққа, ұқыптылыққа, дәлдікке тәрбиелеу, өз біліміне жауапкершілікпен қарауға дағдыландыру.
2
Анаграмма
Ответы:
7
Ұшқыр ойдан ,ұтымды жауап
1.ах² + b х+с=0 түріндегі көпмүше квадрат үшмүше ме?
ия
2.Квадрат үшмүшені нөльге айналдыратын х айнымалысының мәндері квадрат үшмүшенің түбірлері бола ма ?
ия
3.Квадрат үшмүшенің түбірлері болмаса, квадрат үшмүше көбейткіштерге жіктеледі.
жоқ, себебі түбірлері жоқ
4.Егер квадрат үшмүше көбейткіштерге жіктелсе, онда оның түбірлері бар болады
ия
жоқ ,таңбасында қате бар
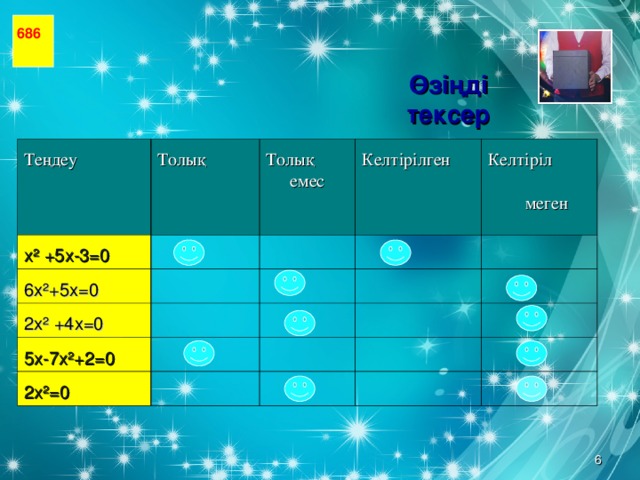
686
Өзіңді тексер
Теңдеу
Толық
х² +5х-3=0
6х²+5х=0
Толық емес
Келтірілген
2х² +4х=0
Келтіріл меген
5х-7х²+2=0
2х²=0
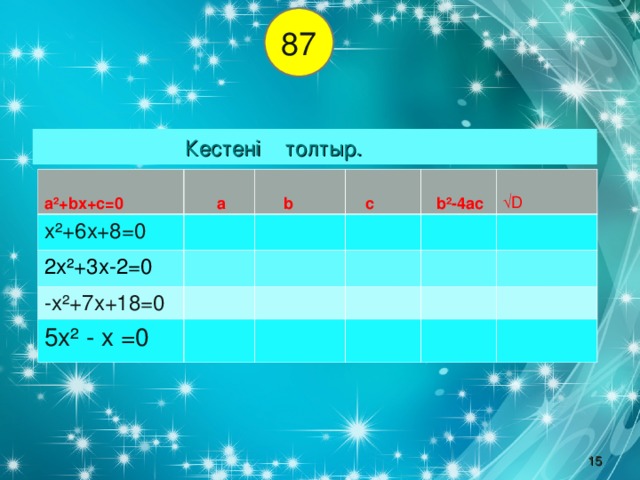
87
Кестені толтыр.
а²+ b х+с=0
а
х²+6х+8=0
b
2х²+3х-2=0
-х²+7х+18=0
с
5х² - х =0
b ²-4ас
√ D
15
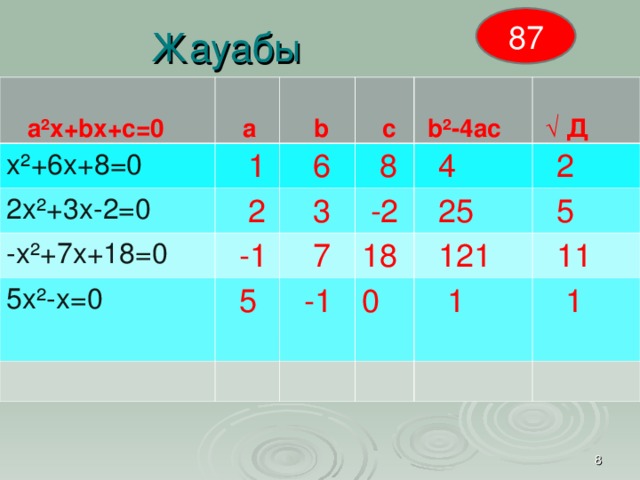
87
Жауабы
а²х+ b х+с=0
а
х²+6х+8=0
1
2х²+3х-2=0
b
-х²+7х+18=0
с
6
2
b ²-4ас
8
-1
3
5х²-х=0
7
-2
√ Д
4
5
2
18
25
-1
5
121
0
11
1
1
0, теңдеудің әртүрлі екі түбірі болады Егер х 1 және х 2 квадрат үшмүшенің түбірлері болса," width="640"
Квадрат теңдеулерді формула арқылы шешу.
а х² + bх + c=0
D көбейткіштерге жіктелмейді
D =0 ,бір түбірі болады
D0, теңдеудің әртүрлі екі түбірі болады
Ауызша есептер
10
1.х 2 -3х-4=0 теңдеуін шешпестен түбірін тап. х 1 =, х 2 =
(-1; 4)
2. Квадраттық үшмүше мына көбейтінді түрінде жіктелген: 4(х+8)(х-19). Түбірін тап.
(-8;19)
3.Түбірлері х 1 , х 2 болатын теңдеуді жаз. х 1 =6, х 2 = -2
(х 2 - 4х-12 =0)
4.а- ның қандай мәнінде теңбе- теңдік тура: х 2 + 3х+а = (х+2)(х+1)
(а =2)
11
Жаттығуды орындаңдар
а) х 1 = 1, х 2 = -2.
б) х 1 = - 5, х 2 = - 3.
в) х 1 = 9 , х 2 =- 11 .
Тексеру :
а) х 2 +х-2=0
б) х 2 +8х+15=0
в) х 2 +2х-99=0
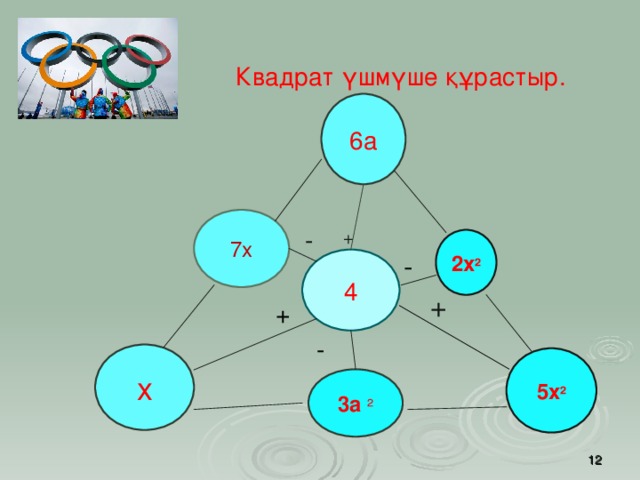
Квадрат үшмүше құрастыр.
6а
7х
-
+
2х ²
-
4
+
+
-
х
5х ²
3а ²
«Кім жылдам». Деңгейлік тапсырмалар
І деңгей.(1 ұпай)
ІІ деңгей. ( 2 ұпай ) Түбірлерін табыңдар:
1) х²-4х+3 2) х²-3х-18 3) х² +3х-10
ІІІ деңгей. ( 3 ұпай) Көбейткіштерге жіктеңдер.
1) 15х²+х+2 2) 5х²+8х+3 3) 2х²-5х+2
Жауаптары :
1деңгей. 1) а=3, b= -5 , с= -2 2) а=-5, b= 2 ,с=-3 3 ) а=-16 , b= 6 ,с=1
2 деңгей: 1 ) х 1 =1, х 2 =3 2 ) х 1 =-3, х 2 =6 , 3 ) х 1 =-5, х 2 =2 3 деңгей : 1) 15(х-0,3)(х+0,4) 2) 5(х+1)(х+0,6) 3) 2(х-2)(х-0,5)
С тобы
1300
Бөлшекті қысқарт:
3500
Есеп шығар
Көбейткіштерге жікте
1 нұсқа
1) Х 2 – 16 =
2) Х 2 –Х + 4 =
3) Х 2 – 5Х + 4 =
2 нұсқа
1) Х 2 – 25 =
2) Х 2 –8х +15 =
3) Х 2 + 3Х + 5 =
Жауап : 1 нұсқа
2 ) Жіктелмейді Д
3) (х-1)(х-4)
2 нұсқа
3500 олимпиада ойындарына қ атысатын спортшылар саны
Сөзжұмбақ
1
Д
3
и
Б
5
с
и
9
4
2
к
Т
к
к
в
В
Р
о
ү
р
а
э
б
а
и
и
6
і
8
д
ф
е
д
м
к
ф
р
Р
и
т
и
р
е
и
7
а
а
к
н
ц
т
л
11
т
а
10
а
ц
т
и
б
ш
13
л
о
н
и
е
е
і
ө
т
ф
о
л
ң
н
12
г
о
ы
н
р
а
т
д
р
м
і
т
б
е
л
м
с
л
е
е
у
г
ы
о
р
е
з
р
л
н
а
е
м
а
3500
Есепті шеш
Жауабыңды тексер :
1.х²+3х-88=0
2. х 1= - 8 х 2= 1
3. х 1= - 1/5 , х 2= 1
«Сөзжұмбақ».
1. b 2 –4 ac өрнегін қалай атайды?
2. Квадрат теңдеудің түбірлері туралы теорема қай ғалымның есімімен аталған?
3. ах 4 + вх 2 + с =0 түріндегі теңдеу қалай аталады?
4. Түбір белгісінің басқаша атауы.
5. Теңдеуді шешкенде табылатын сан.
6. Теңдеудің түрі.
7. в =0 немесе с =0, болмаса в =0, с =0 болатын квадрат теңдеудің түрі.
8. а =1 болатын квадрат теңдеу.
9. Квадрат теңдеудегі а , в қалай аталады?
10. Геометриялық фигура.
11. Теңдеуді қанағаттандырмайтын түбір.
12. Дәлелдеуді қажет ететін тұжырым.
13. Теңдеуді шешуге көмектесетін өрнек.
Тест (1ұпай)
1 . Бұл көпм ү ше ax 2 +bx+c
a/ квадрат теңдеуі в/ квадрат үшмүше c/ квадраттық функция d/ квадрат теңсіздік
2. ax 2 +bx+c=0- бұл
a/ квадрат теңдеуі в/ квадрат үшмүше c/ квадраттық функция d/ квадрат теңсіздік
3. x 2 +px+q =0- б ұл
a/ квадрат теңдеуі в/ толымсыз квадрат теңдеуі c/келтірілген квадрат теңдеуі d/ квадрат теңдеуі
4. Берілген өрнектердің ішінен квадрат үшмүшені табыңдар :
a/ 2x+3 в / x 3 -x 2 +5 c/ x 2 -19x+5 d/ 3x 2 -0 , 4x-x 3
5 . ax 4 +bx 2 +c=0- бұл
a/ квадрат теңдеуі в / биквадрат теңдеуі c/ келтірілген квадрат теңдеуі d/ квадрат үшмүше
6 . Дискриминант формуласы қайысы ?
a / D=b+4ac в / D=b-4ac 2 c/ D=b-4a 2 c d/ D=b 2 -4ac
0 в / D11. х 2 - 9х+8 көбейткіштерге жікте : a/ (х-1)(х-8) b/ (х+1)(х-9) c/ (х+1)(х+8) d/ жіктеуге болмайды 12. 2х 2 -10х+12 көбейткіштерге жікте : a/ (2х-4)(х+3) b/ 2(х-2)(х-3) c/ 2 (х+2)(х+3) d/ (х-2)(х-3)" width="640"
7. 4 х 2 -8х+4=0 дискриминанты неге тең ? а/ 4 в/ 16 с/ 36 d/ 0 8. Көбейткіштерге жікте : 9- 4 х 2
a/ (3+2х)(3+2х) в/ (3-2х)(3+2х) c/ (3-2х)(3-2х) d/ жіктеуге болмайды
9. Келтірілген квадрат теңдеуді табыңдар :
a/ 2x+3 в / x 3 -x 2 +5 c/ x 2 -19x+5 d/ 3x 2 -0.4x-x 3
10 . Қай кезде квадрат теңдеуінде шешімі болмайды ?
a/ D0 в / D
11. х 2 - 9х+8 көбейткіштерге жікте :
a/ (х-1)(х-8) b/ (х+1)(х-9) c/ (х+1)(х+8) d/ жіктеуге болмайды
12. 2х 2 -10х+12 көбейткіштерге жікте :
a/ (2х-4)(х+3) b/ 2(х-2)(х-3) c/ 2 (х+2)(х+3) d/ (х-2)(х-3)
Тест Тест жауабы
Сұрақ
1
Жауап
2
В
3
А
С
4
5
С
6
В
7
Д
Д
8
9
В
С
10
11
В
12
А
В
«Дарындылық – бұл 1% ,
еңбектеніп тер төгу 99% ».
Эдисон Т.
Рефлексия:
- сабақ ұнады ма?
-несімен ұнады?
-қай топ оқушылары жақсы қатысты ?
Ү йге тапсырма
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
