Тема урока: Как построить графики функции y= f(x+a); y=f(x)+a; y=f(x+a)+b, если известен график функции y=f(x).
Цель урока: Выяснить от чего зависит движение графика функции вправо, влево по оси 0х; вверх, вниз по оси 0у; одновременное движение по осям 0х и 0у.
Научиться выполнять построение графиков, используя параллельный перенос вдоль осей.
Научиться ставить перед собой цель, и пути ее достижения.
Формулировать новые понятия, в результате разрешения проблемной ситуации.
Воспитывать умение общаться, вести диалог, активность, стремление проявить себя.
Ход урока:
- Актуализация знаний
Цель: контроль знаний, подведение детей к изучению нового.
Слайд I
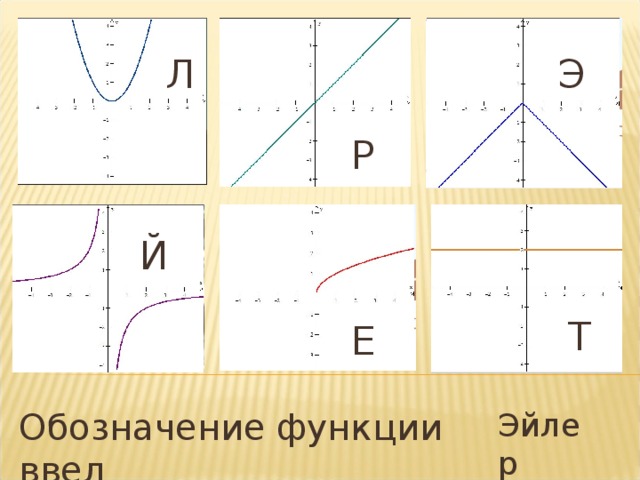
Перед вами зашифрованное задание, ответив на мои вопросы мы узнаем фамилию ученого, который впервые ввел обозначение функции. Выбрав верный ответ, в тетрадях запишите соответствующую верному ответу букву.
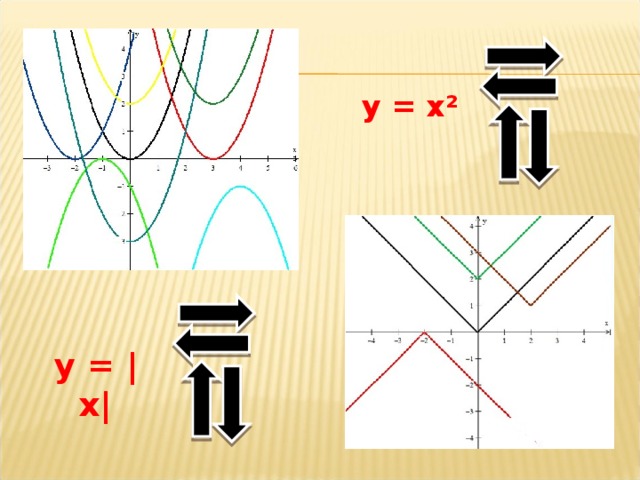
- Укажите график функции, симметричный графику функции у=|x| относительно оси абсцисс. Э
- Укажите график функции, которая претерпевает разрыв в точке х=0 Й
- Укажите график функции, убывающей на промежутке (-∞;0] Л
- Укажите функцию, область определения которой промежуток [0;+∞) Е
- Укажите график прямой зависимости Р
Один ученик записывает результаты на доске, трое сдают тетради на проверку учителю, остальные проверяют работу, ставят оценки.
- Проверка домашнего задания.
Цель: контроль умений и навыков, полученных на предведущих уроках, умений анализировать, сравнивать, подведение учащихся к восприятию нового.
Слайд II
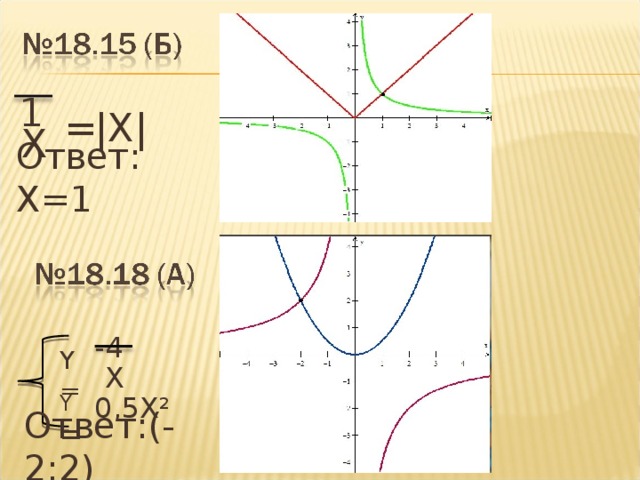
№ 18.15б|
1) у =1/х график функции явная гипербола
х
-2
-1
-1/2
-1/3
-1/2
1/3
1/2
2
у
-1/2
-1
-2
-3
-2
3
2
1/2
2) у=|х|
Ответ х=1
Слайд III
№ 18.18а
Ответ: (-2;2)
Слайд IV
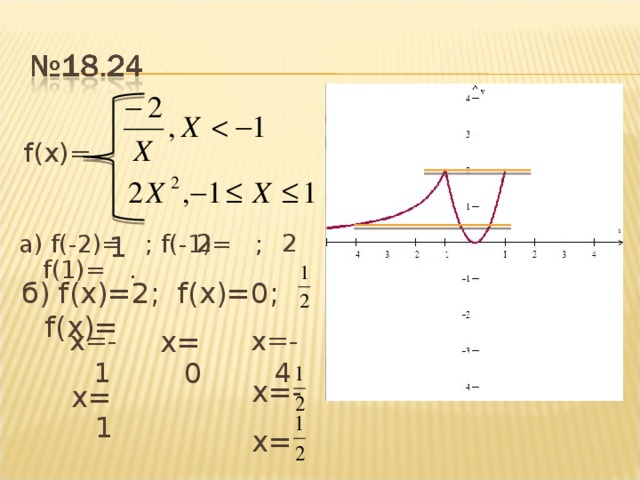
№ 18.24
f(x)
у=– , х < –1 графиком функции является часть гиперболы.
у=2х2, –1≤ х ≤ 1 графиком функции является часть параболы.
а) f(-2)=1; f(-1)= 2; f(1)=2
б) f(x)=2 f(x)=0 f(x)=1/2
x1=–1 x=0 x1=–4
x2=1 x2= 1/2
x3= –1/2
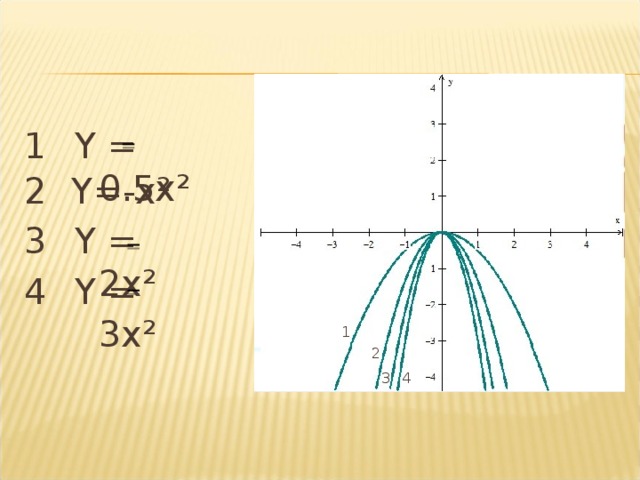
Сравните часть параболы в №18.24 и в №18.18. В №18.24 часть параболы сжата сильнее, чем в №18.18. От чего зависит, сжимается парабола или перемещается вдоль оси 0у? (от коэффициента а)
Слайд V
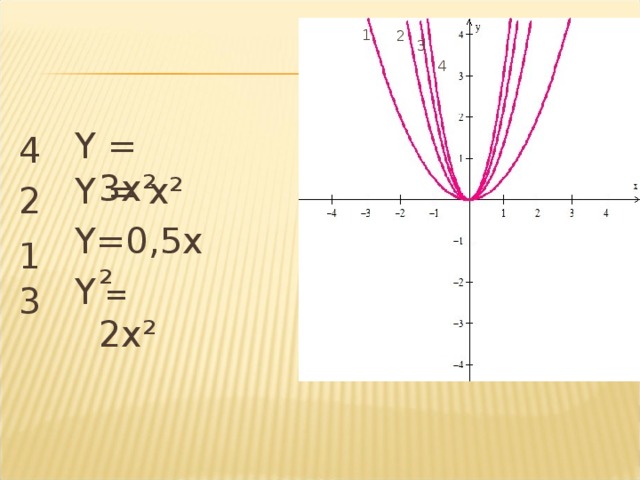
Сравните данные формулы, сопоставьте графики, назовите коэффициенты.
– Что произошло с параболами? (Ветви парабол сжимаются).
1. у=0,5х2 2. у=х2 3. у=2х2 4. у=3х2
Слайд VI
– Что происходит с параболами? По чему они зеркально отразились относительно оси 0х?
От чего это зависит? (коэффициент а<0)
1. у=–0,5х2 2. у=–х2 3. у=–2х2 4. у=–3х2
Слайд VII
Объяснение нового материала.
На этом чертеже происходит движение параболы у= х2
Как вы думаете, чем будем заниматься сегодня на уроке?
- Выясним, от чего зависит перемещение параболы вдоль осей 0х, 0у и одновременно.
- Будем учиться строить такие графики со смещением.
Практическая работа. (на доске)
- Строим систему отсчета.
- Строим у=х2
- I y=(x+2)2
II y=x2+2
III y=–(x–1)2
IV y=(x–3)2
V y=x2–1
Слайд VII
Презентация ученика «Графики функций» (анализируем, сравниваем, делаем выводы)
Как построить график функции, если известен график функции у=f(x)
Сделаем вывод:
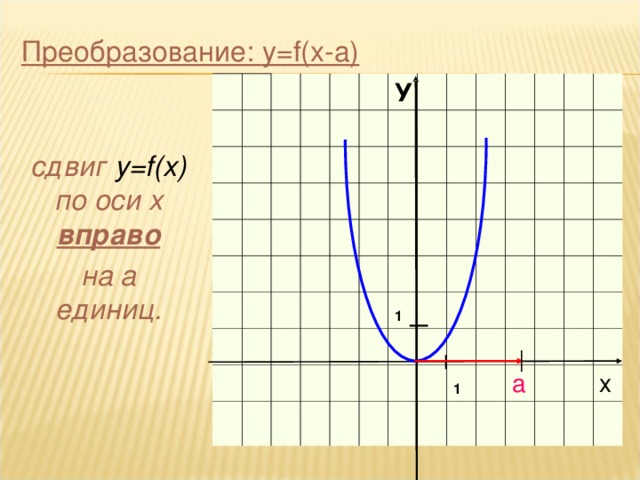
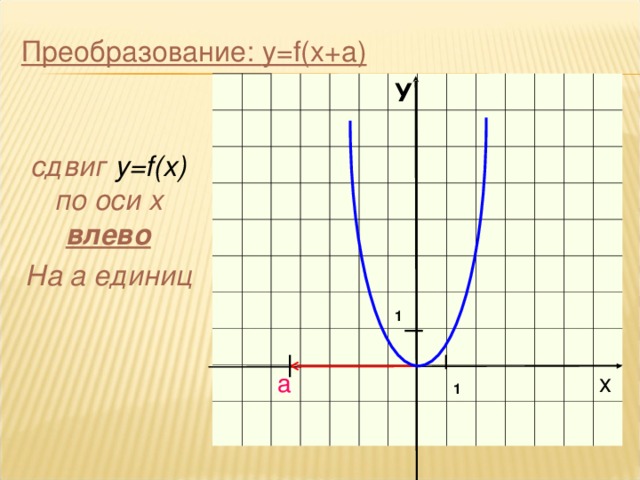
- у=f(х+а): из у=f(x) перемещается влево на а единиц по оси 0х
у=f(х–а): из у=f(x) перемещается вправо на а единиц по оси 0х
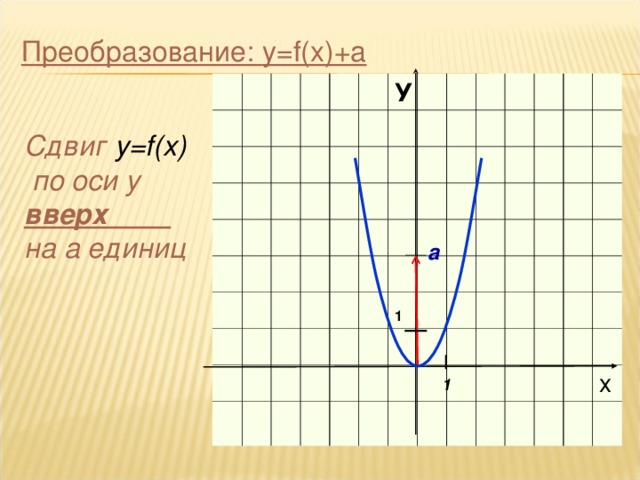
- y=f(x)+a: из y=f(x) перемещается вверх на а единиц по оси 0у
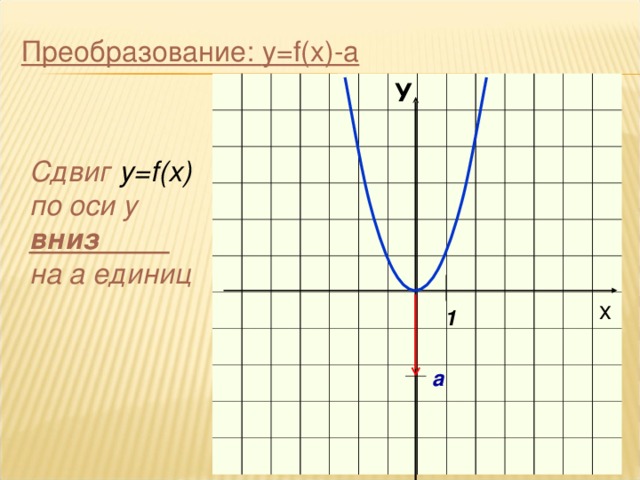
y=f(x)–a: из y=f(x) перемещается вниз на а единиц по оси 0у
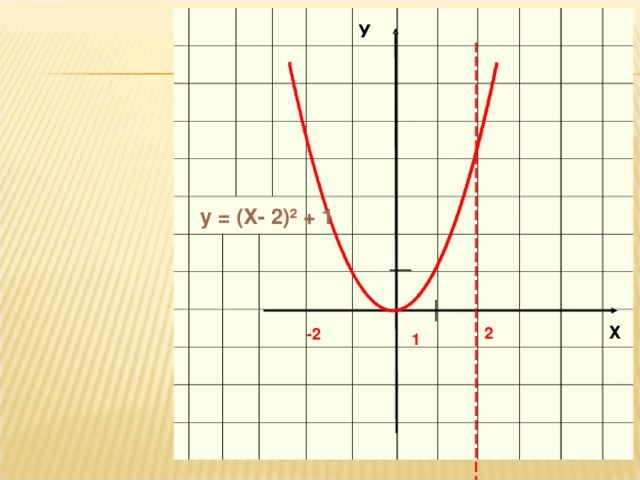
- y=f((x±a)±b: из y=f(x) перемещается (вправо-влево на а единиц по оси 0х) вверх-вниз на b единиц по оси 0у
На доске:
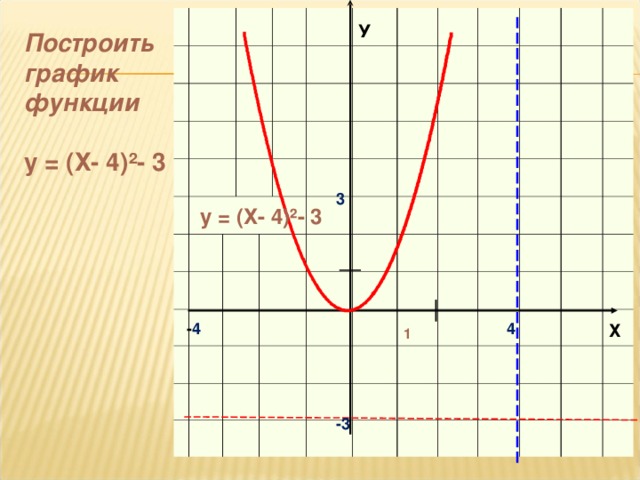
Как построить график функции у=(х+4)2–3: из у=х2 перемещается влево на 4 единице по оси 0х и вниз на 3 единице по оси 0у
Вершина (–4; 3)