Что нам стоит дом постороить

ЧТО НАМ СТОИТ ДОМ ПОСТРОИТЬ?

ПОСТРОЕНИЕ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ.

НЕМНОГО ИСТОРИИ

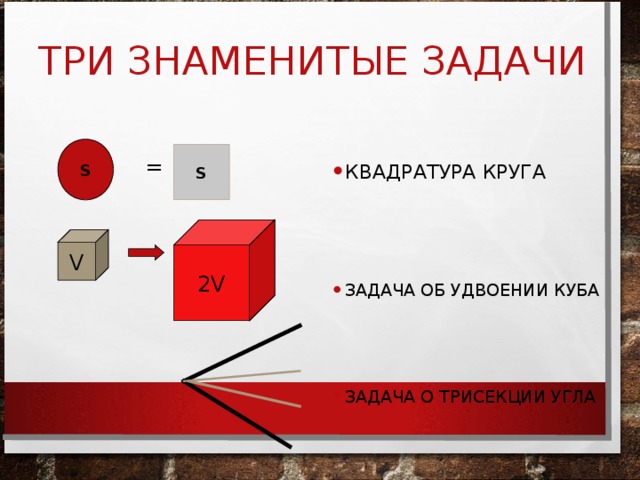
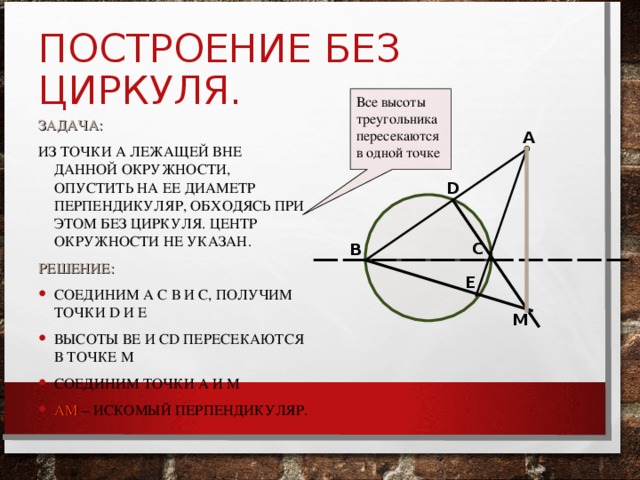
• ИСКУССТВО ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИХ ФИГУР БЫЛО В ВЫСОКОЙ СТЕПЕНИ РАЗВИТО В ДРЕВНЕЙ ГРЕЦИИ. ДРЕВНЕГРЕЧЕСКИЕ МАТЕМАТИКИ ЕЩЕ 3000 ЛЕТ НАЗАД ПРОВОДИЛИ СВОИ ПОСТРОЕНИЯ С ПОМОЩЬЮ ДВУХ ПРИБОРОВ: ГЛАДКОЙ ДОЩЕЧКИ С РОВНЫМ КРАЕМ (ЭТО ЛИНЕЙКА) И ДВУХ ЗАОСТРЕННЫХ ПАЛОК, СВЯЗАННЫХ НА ОДНОМ КОНЦЕ (ЭТО ЦИРКУЛЬ). ОДНАКО ЭТИХ ПРОСТЕЙШИХ ИНСТРУМЕНТОВ ОКАЗАЛОСЬ ДОСТАТОЧНО ДЛЯ ВЫПОЛНЕНИЯ ОГРОМНОГО МНОЖЕСТВА РАЗЛИЧНЫХ ПОСТРОЕНИЙ. ДРЕВНИМ ГРЕКАМ ДАЖЕ КАЗАЛОСЬ, ЧТО ЛЮБОЕ РАЗУМНОЕ ПОСТРОЕНИЕ МОЖНО СОВЕРШИТЬ ЭТИМИ ИНСТРУМЕНТАМИ, ПОКА ОНИ НЕ СТОЛКНУЛИСЬ С ТРЕМЯ ЗНАМЕНИТЫМИ ВПОСЛЕДСТВИИ ЗАДАЧАМИ.

ТРИ ЗНАМЕНИТЫЕ ЗАДАЧИ

• КВАДРАТУРА КРУГА
• ЗАДАЧА ОБ УДВОЕНИИ КУБА
• ЗАДАЧА О ТРИСЕКЦИИ УГЛА

S

S

=

2V

V

ЭВАРИСТА ГАЛУА

ТОЛЬКО В XΙX ВЕКЕ БЫЛО ДОКАЗАНО, ЧТО ВСЕ ТРИ ЗАДАЧИ НЕ ИМЕЮТ РЕШЕНИЯ. ВОПРОС НЕВОЗМОЖНОСТИ ПОСТРОЕНИЯ ПОЛНОСТЬЮ РЕШЕН АЛГЕБРАИЧЕСКИМИ МЕТОДАМИ, ОСНОВАННЫМИ НА ТЕОРИИ ГАЛУА.

• ЛИНЕЙКА НЕ ИМЕЕТ ДЕЛЕНИЙ И ИМЕЕТ ТОЛЬКО ОДНУ СТОРОНУ БЕСКОНЕЧНОЙ ДЛИНЫ.
• ЦИРКУЛЬ ИМЕЕТ СКОЛЬ УГОДНО БОЛЬШОЙ РАЗМЕР

В ЗАДАЧАХ НА ПОСТРОЕНИЕ ВОЗМОЖНЫ СЛЕДУЮЩИЕ ОПЕРАЦИИ, ИЗВЕСТНЫЕ С ДРЕВНИХ ВРЕМЕН:

• ВЫБОР ПРОИЗВОЛЬНОЙ ТОЧКИ НА ПЛОСКОСТИ
• НАХОЖДЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ДВУХ ПОСТРОЕННЫХ ЛИНИЙ.
• ВЫБОР ТОЧКИ НА ПРЯМОЙ

• С ПОМОЩЬЮ ЛИНЕЙКИ ПРОВЕСТИ ПРЯМУЮ, ПРОХОДЯЩУЮ ЧЕРЕЗ ДВЕ ПОСТРОЕННЫЕ ТОЧКИ.

• С ПОМОЩЬЮ ЦИРКУЛЯ ПРОВЕСТИ ОКРУЖНОСТЬ С ЦЕНТРОМ В ПОСТРОЕННОЙ ТОЧКЕ И С РАДИУСОМ, РАВНЫМ РАССТОЯНИЮ МЕЖДУ ДВУХ ПОСТРОЕННЫХ ТОЧЕК.

ПОСТРОЕНИЕ ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА

• ПОСТРОИМ ОКРУЖНОСТЬ РАДИУСОМ R
• ОТМЕТИМ НА ОКРУЖНОСТИ ПРОИЗВОЛЬНУЮ ТОЧКУ А
• НЕ МЕНЯЯ РАСТВОРА ЦИРКУЛЯ, ПОСТРОИМ НА ЭТОЙ ОКРУЖНОСТИ ТОЧКИ А 1; А 2; А 3; А 4; А 5
• СОЕДИНИМ ПОСЛЕДОВАТЕЛЬНО ПОЛУЧЕННЫЕ ТОЧКИ
• ПОЛУЧЕННЫЙ МНОГОУГОЛЬНИК – ИСКОМЫЙ.

А 2

А 1

А 3

А

А 4

А 5

РАЗБИЕНИЕ ОТРЕЗКА НА ДВЕ РАВНЫЕ ЧАСТИ.

• ЦИРКУЛЕМ И ЛИНЕЙКОЙ ПРОВОДИМ ОКРУЖНОСТЬ С ЦЕНТРОМ В ТОЧКЕ А И РАДИУСОМ АВ
• ПРОВОДИМ ОКРУЖНОСТЬ С ЦЕНТРОМ В ТОЧКЕ В РАДИУСОМ АВ
• НАХОДИМ ТОЧКИ ПЕРЕСЕЧЕНИЯ P И Q ДВУХ ПОСТРОЕННЫХ ОКРУЖНОСТЕЙ
• ЛИНЕЙКОЙ ПРОВОДИМ ОТРЕЗОК, СОЕДИНЯЮЩИЙ ТОЧКИ P И Q
• НАХОДИМ ТОЧКУ ПЕРЕСЕЧЕНИЯ АВ И PQ ТОЧКУ К. К – ИСКОМАЯ СЕРЕДИНА ОТРЕЗКА АВ

P

К

B

A

Q

ОКРУЖНОСТЬ АПОЛЛОНИЯ

• СТРОИМ ТОЧКИ P И Q, ДЕЛЯЩИЕ ДАННЫЙ ОТРЕЗОК АВ В ДАННОМ ОТНОШЕНИИ, ИСПОЛЬЗУЯ ТЕОРЕМУ ФАЛЕСА
• НА ОТРЕЗКЕ PQ КАК НА ДИАМЕТРЕ ОПИСЫВАЕМ ОКРУЖНОСТЬ.
• ЭТО И ЕСТЬ ОКРУЖНОСТЬ АПОЛЛОНИЯ.

A

P

B

m

Q

n

n

m

n

ПОСТРОЕНИЯ ОДНИМ ЦИРКУЛЕМ.

С ПОМОЩЬЮ ОДНОГО ЦИРКУЛЯ МОЖНО ПОСТРОИТЬ ЛЮБУЮ ФИГУРУ, КОТОРУЮ МОЖНО ПОСТРОИТЬ ЦИРКУЛЕМ И ЛИНЕЙКОЙ. ПРИ ЭТОМ ПРЯМАЯ СЧИТАЕТСЯ ПОСТРОЕННОЙ, ЕСЛИ НА НЕЙ ЗАДАНЫ ДВЕ ТОЧКИ.

ПО ТЕОРЕМЕ МОРА – МАКЕРОНИ.

ПОСТРОЕНИЕ ТОЧКИ, СИММЕТРИЧНОЙ ДАННОЙ ОТНОСИТЕЛЬНО ДАННОЙ ПРЯМОЙ.

• СТРОИМ ОКРУЖНОСТЬ (А;АС)
• СТРОИМ ОКРУЖНОСТЬ (В;ВС)
• ОКР.(А;АС)
• К - ИСКОМАЯ ТОЧКА

К

В

А

окр.(В;ВС)= К

С

ПОСТРОЕНИЕ ОДНОЙ ЛИНЕЙКОЙ.

• В 1833 ГОДУ ШВЕЙЦАРСКИЙ ГЕОМЕТР ЯКОБ ШТЕЙНЕР ОПУБЛИКОВАЛ РАБОТУ, В КОТОРОЙ ПОЛНО ИССЛЕДОВАЛ ПОСТРОЕНИЯ ОДНОЙ ЛИНЕЙКОЙ. В РАБОТЕ ОН ДОКАЗАЛ ТЕОРЕМУ:

«КАЖДАЯ ЗАДАЧА НА ПОСТРОЕНИЕ, РАЗРЕШИМАЯ ЦИРКУЛЕМ И ЛИНЕЙКОЙ, МОЖЕТ БЫТЬ РЕШЕНА И ОДНОЙ ЛИНЕЙКОЙ, ЕСЛИ В ПЛОСКОСТИ ЧЕРТЕЖА ДАНА ПОСТОЯННАЯ ОКРУЖНОСТЬ И ЕЕ ЦЕНТР».

ЭТО ТЕОРЕМА ПОНСЕЛЕ –ШТЕЙНЕРА. (В 1822 ГОДУ ЭТА ТЕОРЕМА БЫЛА ДОКАЗАНА ДРУГИМ СПОСОБОМ ФРАНЦУЗОМ Ж. ПОНСЕЛЕ).

ПОСТРОЕНИЕ БЕЗ ЦИРКУЛЯ.

Все высоты треугольника пересекаются в одной точке

ЗАДАЧА:

ИЗ ТОЧКИ А ЛЕЖАЩЕЙ ВНЕ ДАННОЙ ОКРУЖНОСТИ, ОПУСТИТЬ НА ЕЕ ДИАМЕТР ПЕРПЕНДИКУЛЯР, ОБХОДЯСЬ ПРИ ЭТОМ БЕЗ ЦИРКУЛЯ. ЦЕНТР ОКРУЖНОСТИ НЕ УКАЗАН.

РЕШЕНИЕ:

• СОЕДИНИМ А С В И С, ПОЛУЧИМ ТОЧКИ D И E
• ВЫСОТЫ ВЕ И СD ПЕРЕСЕКАЮТСЯ В ТОЧКЕ М
• СОЕДИНИМ ТОЧКИ А И М
• АМ – ИСКОМЫЙ ПЕРПЕНДИКУЛЯР.

А

D

С

В

E

M

ПОСТРОЕНИЕ ДВУСТОРОННЕЙ ЛИНЕЙКОЙ .

ЗАДАЧА:

ПОСТРОИТЬ БИССЕКТРИСУ ДАННОГО УГЛА АВС

РЕШЕНИЕ:

• ПРОВЕСТИ ПРЯМЫЕ ПАРАЛЛЕЛЬНЫЕ СТОРОНАМ УГЛА
• К – ТОЧКА ПЕРЕСЕЧЕНИЯ ЭТИХ ПРЯМЫХ
• ПРОВЕСТИ ПРЯМУЮ ЧЕРЕЗ ВЕРШИНУ УГЛА А И ТОЧКУ К
• АК – ИСКОМАЯ БИССЕКТРИСА

В

К

А

С

ПОСТРОЕНИЕ С ПОМОЩЬЮ ПРЯМОГО УГЛА

прямой угол- две стороны чертежного треугольника

ЗАДАЧА:

РАЗДЕЛИТЬ ДАННЫЙ ОТРЕЗОК ПОПОЛАМ

РЕШЕНИЕ:

• ПОСТРОИМ ПРЯМОУГОЛЬНИК ACBD , ГДЕ АВ – ДИАГОНАЛЬ.
• НАЙДЕМ ТОЧКУ ПЕРЕСЕЧЕНИЯ ДИАГОНАЛЕЙ ПРЯМОУГОЛЬНИКА.
• О – ИСКОМАЯ ТОЧКА

C

О

А

В

D

ЗАДАЧИ И НЕ ТОЛЬКО .

ЗАДАЧИ И НЕ ТОЛЬКО