Данная презентация предназначена для обучающихся 9 классов. Материал можно использовать при подготовке к итоговой аттестации, а также на итоговом уроке по теме "График квадратичной функции". В презентации рассматриваются правила определения коэффициентов квадратного трёхчлена а,b и с., а также зависимость коэффициэнтов от графика квадратичной функции, представлены тренировочные задания и задания для сомостоятельной работы, слайды для проверки выполнения самостоятельной работы.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
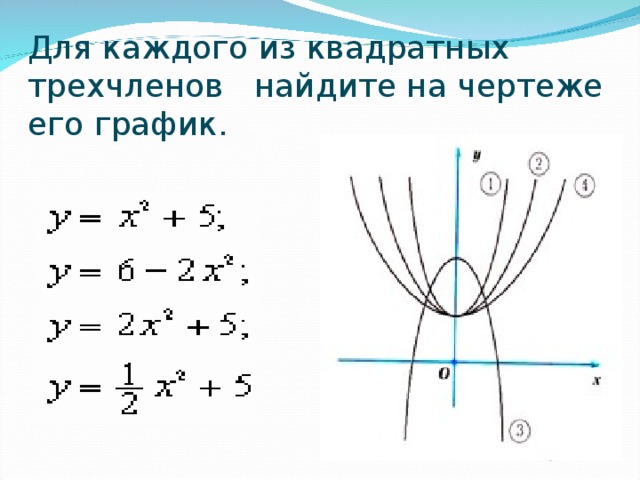
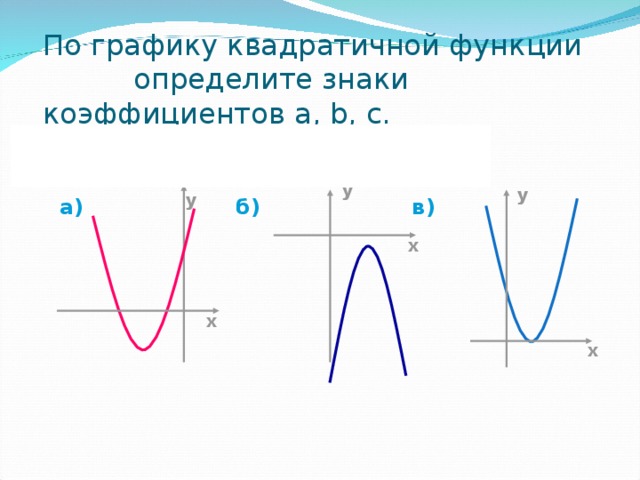
Что может рассказать парабола...
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Что может рассказать парабола... »
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
1740 руб.
2480 руб.
2220 руб.
3170 руб.
2230 руб.
3190 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




 0, то" width="640"
0, то" width="640"


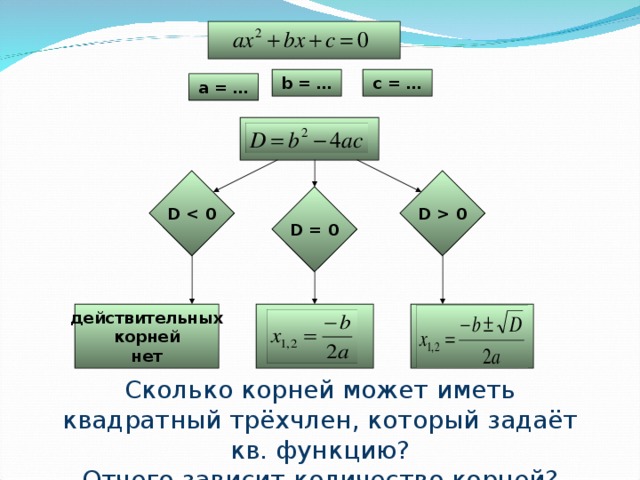 0 D D = 0 действительных корней нет" width="640"
0 D D = 0 действительных корней нет" width="640"
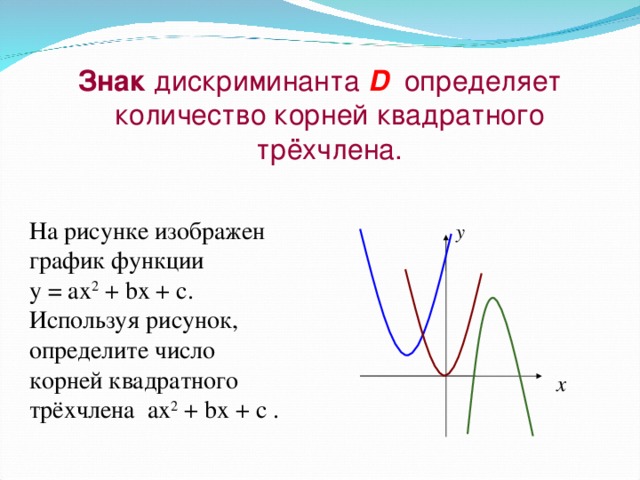
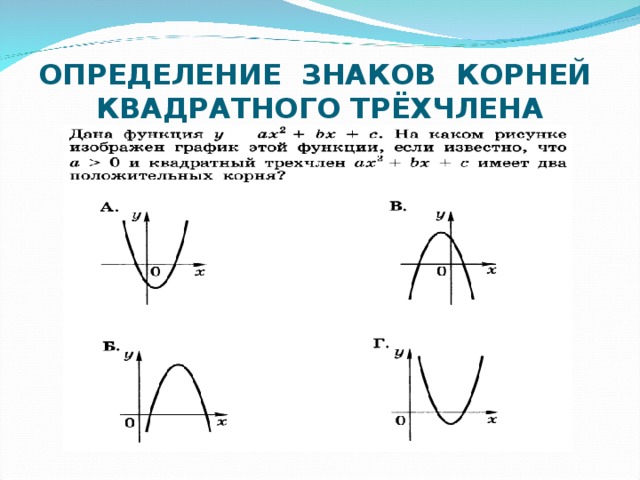
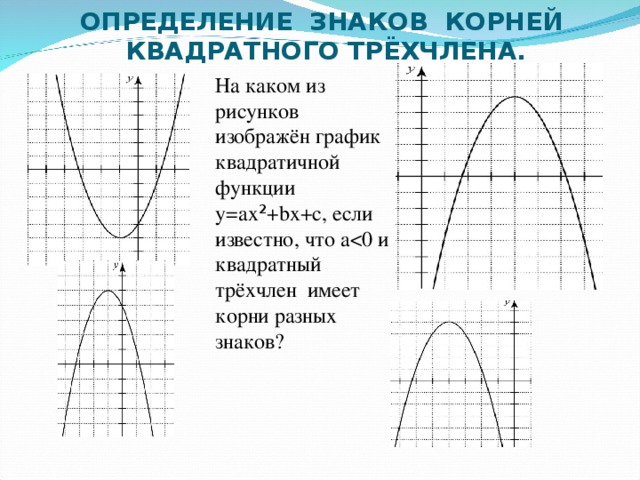
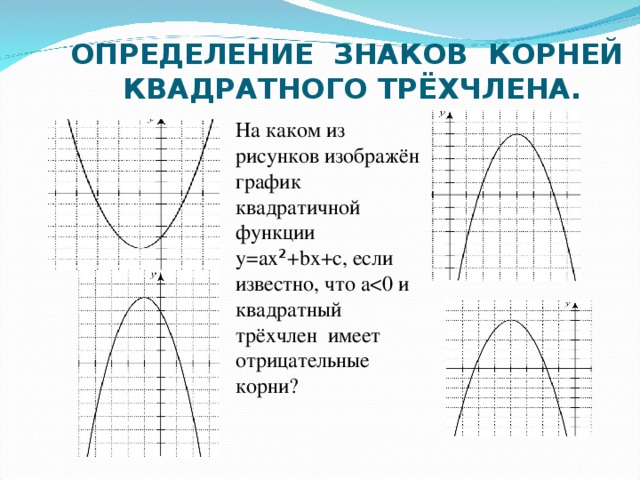
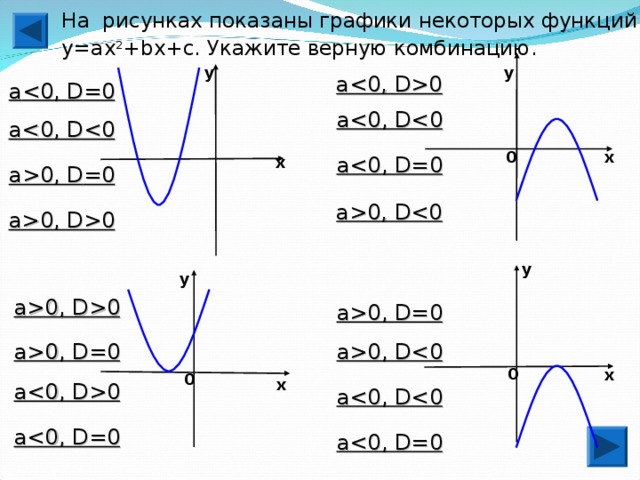 0, D = 0 a0, D a0, D0 у у a0, D0 a0, D=0 a0, D=0 a0, D 0 х 0 х a0 a a a" width="640"
0, D = 0 a0, D a0, D0 у у a0, D0 a0, D=0 a0, D=0 a0, D 0 х 0 х a0 a a a" width="640"

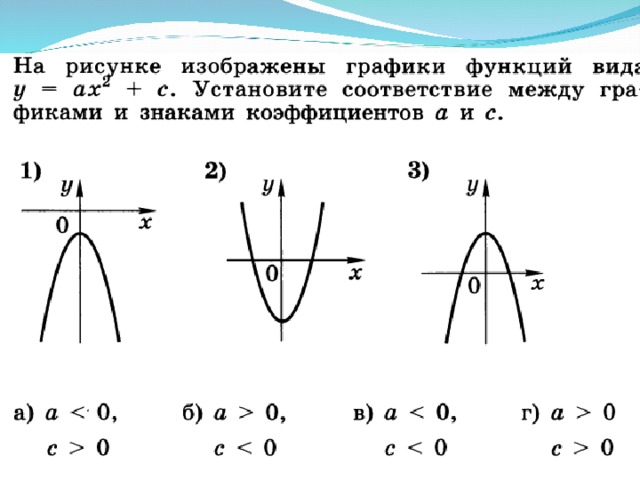
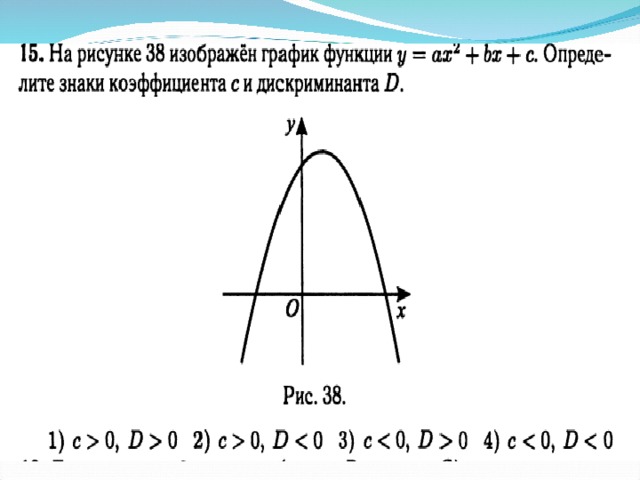
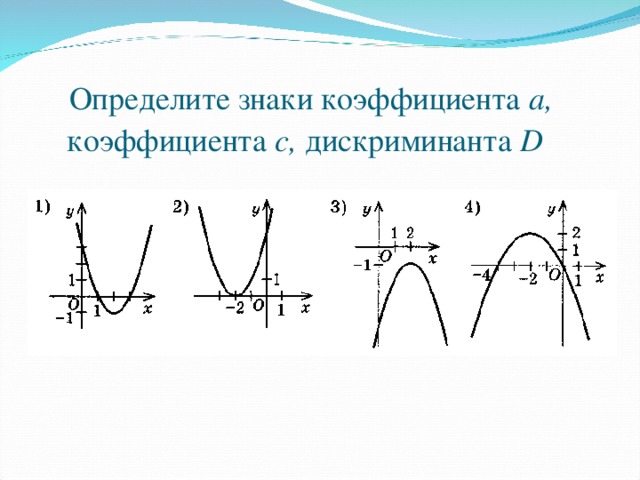
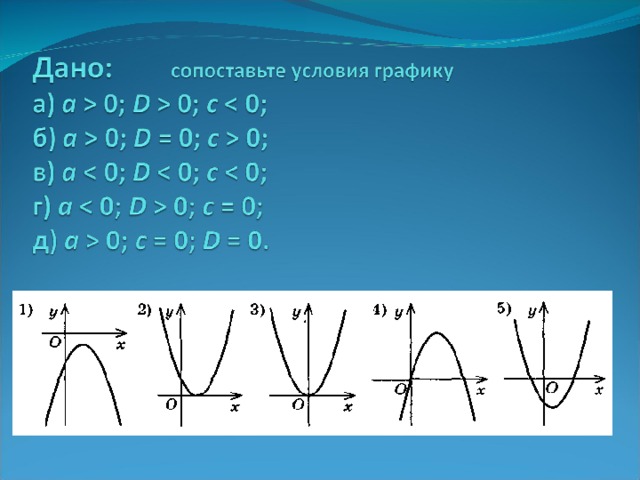

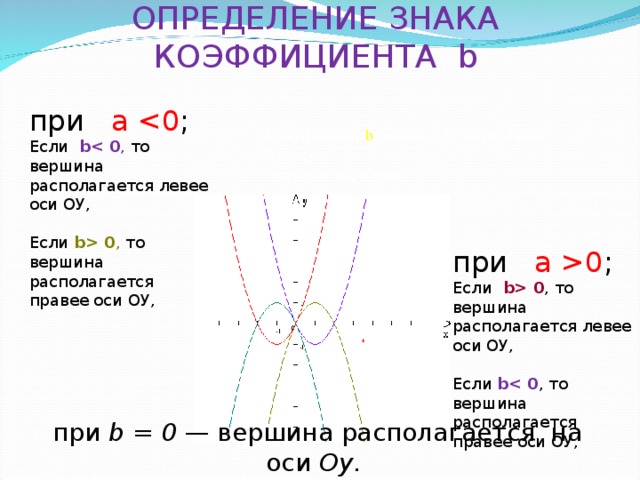 0 , то вершина располагается правее оси ОУ, ) Коэффициент b (вместе с ) определяет абсциссу вершины параболы: при a 0 ; Если b 0 , то вершина располагается левее оси ОУ, Если b 0 , то вершина располагается правее оси ОУ," width="640"
0 , то вершина располагается правее оси ОУ, ) Коэффициент b (вместе с ) определяет абсциссу вершины параболы: при a 0 ; Если b 0 , то вершина располагается левее оси ОУ, Если b 0 , то вершина располагается правее оси ОУ," width="640"
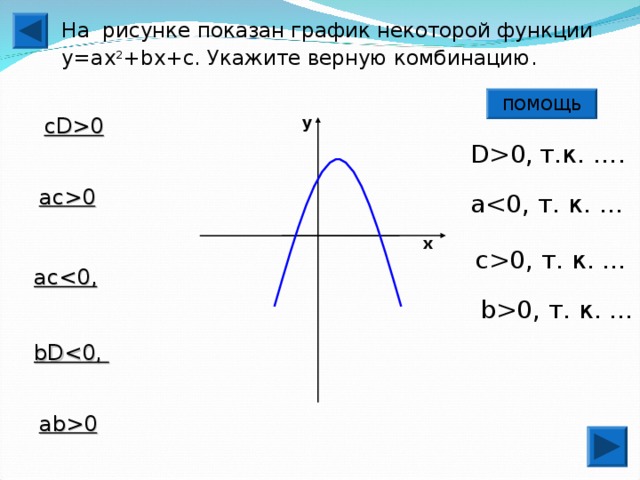 0 D0 , т.к. …. ac0 aх c0 , т. к. … ac b0 , т. к. … bD ab0" width="640"
0 D0 , т.к. …. ac0 aх c0 , т. к. … ac b0 , т. к. … bD ab0" width="640"
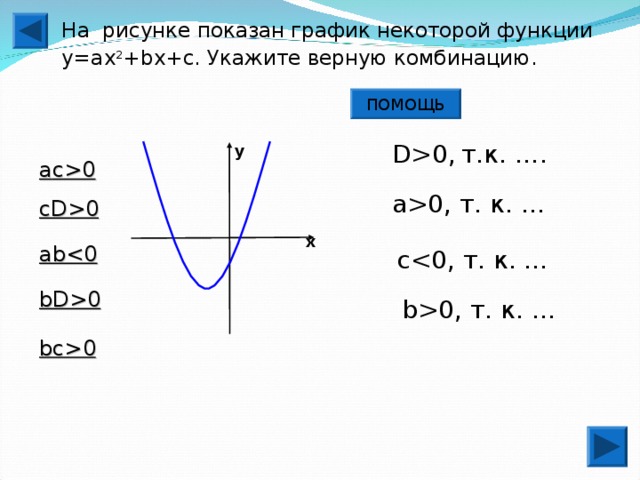 0 , т.к. …. у а c0 a0 , т. к. … cD0 х ab cbD0 b0 , т. к. … bc0" width="640"
0 , т.к. …. у а c0 a0 , т. к. … cD0 х ab cbD0 b0 , т. к. … bc0" width="640"
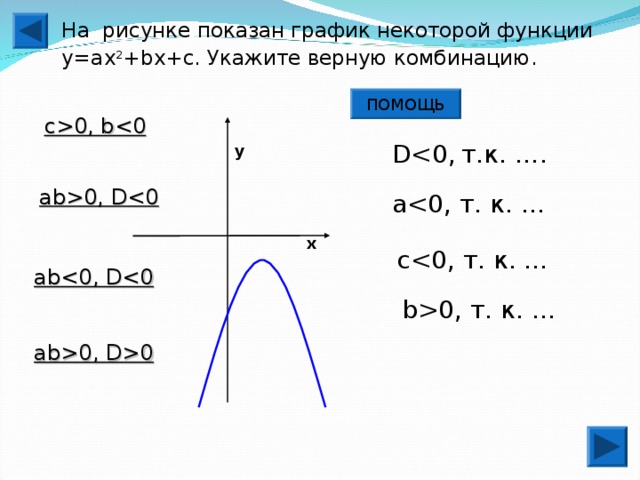 0, b Dу ab0, D aх cab b0 , т. к. … а b0, D0" width="640"
0, b Dу ab0, D aх cab b0 , т. к. … а b0, D0" width="640"

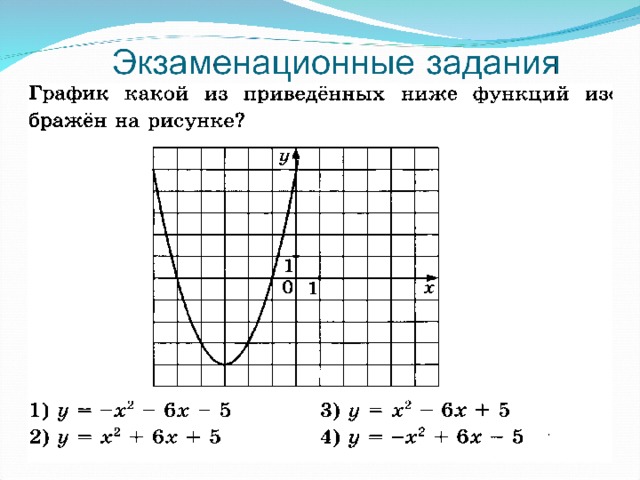

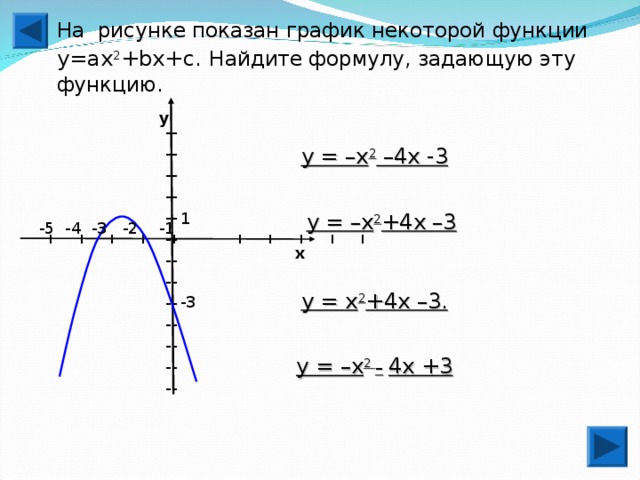
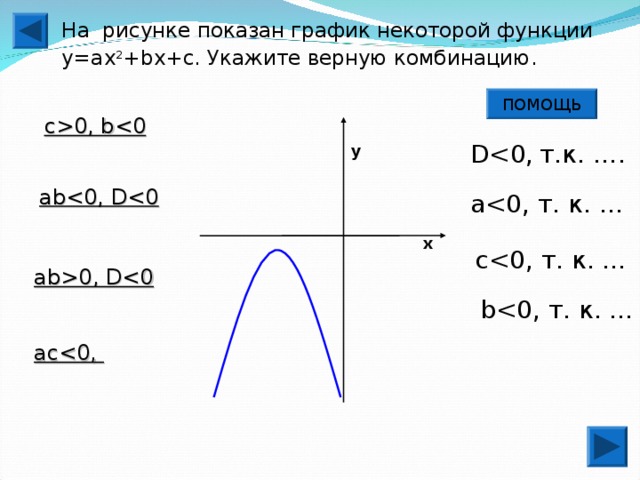 0, b Dу ab aх cab0, D bac" width="640"
0, b Dу ab aх cab0, D bac" width="640"
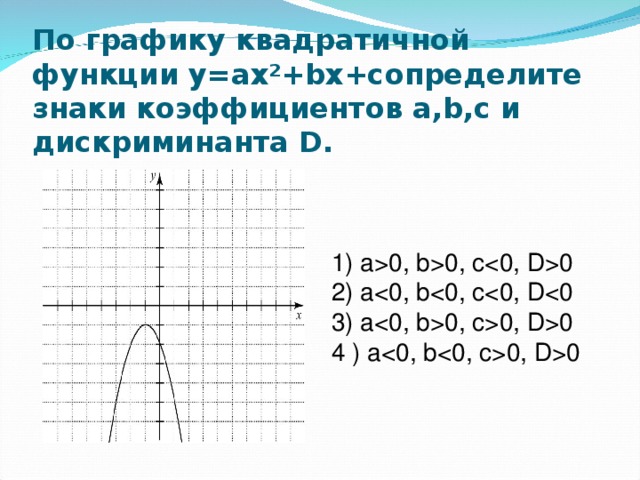 0, b0, c0 2) a0, c0, D0 4 ) a0, D0" width="640"
0, b0, c0 2) a0, c0, D0 4 ) a0, D0" width="640"
 0 (B) Вершина параболы лежит во второй четверти. (C) с ≥ 0 (D) c 0,1 (Е) 10²– 4 ас ≤ 0. у 0" width="640"
0 (B) Вершина параболы лежит во второй четверти. (C) с ≥ 0 (D) c 0,1 (Е) 10²– 4 ас ≤ 0. у 0" width="640"


















