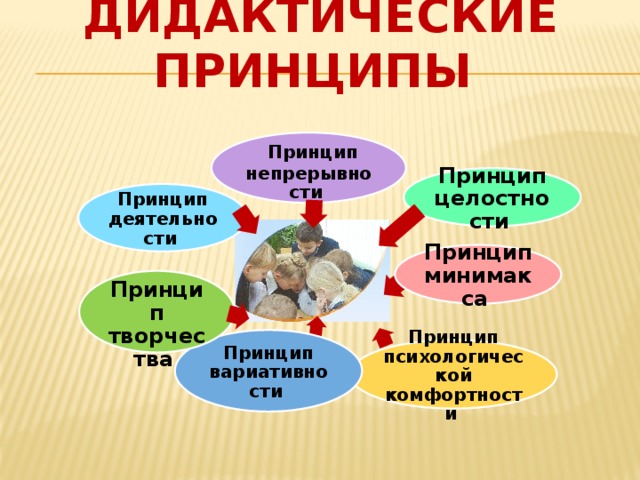
Активные и интерактивные методы обучения как способы активизации учебно-познавательной деятельности учащихся на уроках математики.В Концепции модернизации российского образования сформулированы социальные требования к системе российского образования. Сегодня многие методические новации и инновации связаны с реализацией интерактивного обучения, поскольку именно такое обучение обладает большими потенциальными возможностями для выполнения социального заказа современного общества.В России использование активных и интерактивных методов широко практиковалось в 20-х гг. ХХ в. (проектный, лабораторно-бригадный метод, производственные, трудовые экскурсии, практики). Дальнейшая разработка этих методов присутствует в трудах Сухомлинского (60-егг.), а также “педагогики – сотрудничества” (70-80-егг) - Шаталова, Амонашвили, Лысенковой и других. В последние десятилетия ХХ в. американские коллеги проводили многочисленные эксперименты и научные исследования в области интерактивных методов, разработали детальные руководства для учителей. Все эти методы и наработки способствуют активному использованию интерактивных средств в массовой школе.Вместе с тем следует отметить, что часто преподаватели считают, что для внедрения интерактивного обучения в образовательный процесс просто необходимо наличие компьютера, проектора в учебном кабинете, а лучше всего Smart – доски. Более того, среди учителей математики нередко бытует мнение о том, что единственным условием внедрения интерактивного обучения в образовательную практику является непосредственное использование компьютерных средств обучения. Таким образом, понимание того, что именно стоит за термином «интерактивное обучение», не стало пока достоянием широкой педагогической практики.В педагогике существуют многочисленные классификации методов обучения. Нас интересует, та в основе, которой – роль обучающегося в процессе обучения; традиционно в ней выделяют три метода:1) Пассивный метод 2) Активный метод 3) Интерактивный.Более подробно остановимся на последних двух.Активные методы обучения — методы, позволяющие активизировать учебный процесс, побудить обучаемого к творческому участию в нем. Задачей активных методов обучения является обеспечение развития и саморазвития личности обучаемого на основе выявления его индивидуальных особенностей и способностей. Активные методы обучения позволяют развивать мышление обучаемых; способствуют их вовлечению в решение проблем; не только расширяют и углубляют знания, но одновременно развивают практические навыки и умения.Методы активного обучения это совокупность способов организации и управления учебно-познавательной деятельностью обучаемых, которые обладают следующими основными признаками:
- самостоятельной выработкой решений обучаемым;
- высокой степенью вовлечённости обучаемых в учебный процесс;
- преимущественной направленностью на развитие или приобретения математических умений и навыков;
- постоянной обработкой связью учащихся и учителя, и контролем за самостоятельной работой обучения.
Методы активного обучения обеспечивают и направленную активизацию психических процессов учащихся, т.е. стимулируют мышление при использовании конкретных проблемных ситуаций и проведении деловых игр облегчают запоминание при выделении главного на практических занятиях, возбуждают интерес к математике и вырабатывают потребность к самостоятельному приобретению знаний.
Для организации на занятиях активно познавательной деятельности учащихся решающее значение имеет оптимальное сочетание методов активного обучения. Подбор этих методов можно осуществить по алгоритму, включающему в себя: анализ содержания учебного материала, определение целей урока.Цепь неудач может отвратить от математики и способных детей, с другой стороны, обучение должно идти близко к потолку возможностей ученика: ощущение успеха создаётся пониманием того, что удалось преодолеть значительные трудности. Поэтому к каждому уроку необходимо тщательно подбирать индивидуальные задания, карточки, учитывающие индивидуальные способности учащихся. Дифференцированное обучение способствует развитию интересов и способностей детей. Опыт показывает, что есть множество факторов, формирующих интерес к математике: это возбуждающие любопытство задачи, влияние учителя, родителей, честолюбие и т.д.Наиболее надёжный способ повысить вероятность пробуждения интереса - обеспечить проявление всех этих факторов. Значительное влияние на развитие математических способностей оказывают коллективные обсуждения и работа.Интерактивный метод – форма взаимодействия, ориентированная на более широкое взаимодействие учеников не только с учителем, но и друг с другом и на доминирование активности учащихся в процессе обучения.Отсюда следует, что главная особенность интерактивного обучения в том, что процесс учения происходит в совместной деятельности, а все виды групповой формы могут быть отнесены к формам интерактивного обучения. Сюда же можно отнести и коллективный способ обучения, под которым понимается такая форма организации учебной деятельности, когда один учит всех, а все учат каждого.Главные задачи интерактивных средств обучения: обеспечить диалоговый характер обучения, исключить монологическое преподнесение учебного материала ;исключить дублирование информации, которая может быть получена учащимися самостоятельно из доступных источников;способствовать отработке в различных формах коммуникативных компетенций учащихся. К методам интерактивного обучения относятся те, которые способствуют вовлечению в активный процесс получения и переработки знаний:
Основой реализации интерактивных подходов к содержанию обучения является разработка и использование интерактивных заданий и упражнений, которые будут выполняться учащимися. Основное отличие интерактивных упражнений и заданий от обычных в том, что они направлены не только и не столько на закрепление уже изученного материала, сколько на изучение нового.Именно поэтому каждое интерактивное задание – это творческое учебное задание, которое требует от учащихся не простого воспроизводства информации, а содержит бо/льший или меньший элемент неизвестности и имеет, как правило, несколько подходов.
В чем же заключаются положительные моменты использования интерактивных методов обучения?
При использовании интерактивных методов роль преподавателя резко меняется, перестаёт быть центральной, он лишь регулирует процесс и занимается его общей организацией, готовит заранее необходимые задания и формулирует вопросы или темы для обсуждения в группах, даёт консультации, контролирует время и порядок выполнения намеченного плана.
Психологами было установлено, что в условиях учебного общения наблюдается повышение точности восприятия, увеличивается результативность работы памяти, более интенсивно развиваются такие интеллектуальные и эмоциональные свойства личности, как - устойчивость внимания, умение его распределять; наблюдательность при восприятии; способность анализировать деятельность партнера, видеть его мотивы, цели. Интерактивное обучение помогает ребенку не только учиться, но и жить. Таким образом, интерактивное обучение – несомненно, интересное, творческое, перспективное направление нашей педагогики.