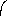"Тікб?рышты ?шб?рышты? с?йір б?рышыны? синусы, косинусы, тангенсі ж?не котангенсі." 8 сынып

«№8 жалпы орта білім беретін көркемдік-эстетикалық білім және тәрбие беру мектеп-кешені»КММ

Математика пәнінің мұғалімі: Батталова Галия Алимгазыевна

Сабақтың тақырыбы: Тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және котангенсі.

Сабақтың мақсаты:

Білімділік: Тікбұрышты үшбұрыштың сүйір бұрышының синусының, косинусының, тангенсінің, котангенсінің анықтамасын түсіндіру, сүйір бұрышының синусының, косинусының, тангенсінің, катангенсінің мәндерін табуға берілген есептерді шығаруға үйрету.

Дамытушылық: Есептер шығару арқылы логикалық ойлау қабілеттерін, математикалық тілде дұрыс сөйлей білу дағдыларын дамыту.

Тәрбиелік: Экологиялық және адамгершілік тәрбиесін беру.

Сабақтың көрнекілігі: Компютер, интерактивті тақта, таратпа материалдар, кесте, білім бағалау парағы.

Сабақтың түрі: Аралас сабақ.

Сабақтың типі: Жаңа білім беру сабағы.

Әдіс – тәсілдері: Сұрақ- жауап, тест, аймақтық компонентті қолдану.

Сабақ жоспары: 1 Ұйымдастыру.

2. Үй тапсырмасын тексеру.

3. Жаңа сабақты меңгерту.

4. Білімді бекіту, тиянақтау.

5. Тест.

6. Қорытындылау.

7. Оқушылар білімін бағалау.

8. Үйге тапсырма.

Сабақтың барысы:

І. Ұйымдастыру. Оқушылардың сабаққа қатысуын, оқу – құрал жабдықтарын түгендеу. Бағалау парағын тарату.

ІІ. Үй тапсырмасын тексеру. «Миға шабуыл»

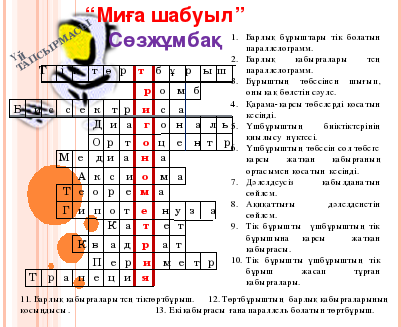
1. Осы тараудың қорытындысы бойынша білімдеріңді тексерейік. Ол үшін оқушылардың құрастырып әкелген есептерін шығарайық. (1-сурет)

2. Айданамен Еркежанның құрастырып әкелген сөзжұмбағын шешейік. Сол арқылы сендердің қандай деңгейде меңгергендеріңді көреміз. Осы сөзжұмбақты дұрыс шешсеңдер, біздің бүгінгі өтетін сабағымызға байланысты терминді аламыз. (1-слайд)

Сонымен біздің сөзжұмбағымыздағы ерекше торкөзде қандай сөз шықты. (тригонометрия)

Тарихи мәлімет:

Тригонометрия элементтерін адамзат ежелгі замандардан бастап, бұрыштарды өлшеу мұқтаждықтары барысында қолдана бастаған. Тригонометриялық фигуралардың қазіргі атаулары ХҮІ – ХҮІІІ ғасырларда пайда болған. Синус сөзі латын тілінен аударғанда «дөңестік» деген мағынаны білдіреді, ал косинустағы «ко» қосымшасы латынның complemeton – толықтауыш деген мағынаны білдіреді. Осы күнгі қолданылып жүрген sinx және cosx белгілеулері 1739 жылы И.Бернуллидің Л.Эйлерге жазған хатында алғаш рет ұсынылған. Бұл белгілеулерді соңынан Л.Эйлер және өзгелер кеңінен қолдана бастады.

ІІІ. Жаңа сабақ: «Мағынаны ашу».

Біз бүгін жаңа тарау бастаймыз. Тік бұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатыстар.

Осы тараудың алғашқы тақырыбы: Тіктөртбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және катангенсі. (2-слайд)

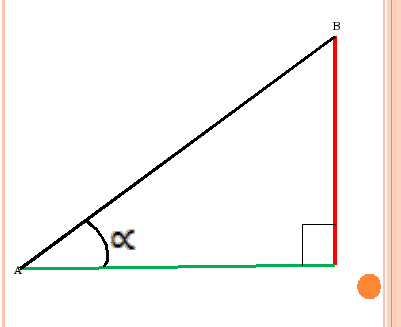
Интерактивті тақтада тікбұрышты үшбұрыш сызбасы көрсетіледі.

(3-слайд)

C = 90о болсын

1. Тік бұрышты ұшбұрыштың сүйір бұрыштары қайсылары?

2. а сүйір бұрышына қарсы жатқан катетті атаңдар?

3. а сүйір бұрышына іргелес жатқан катет?

Бүгінгі сабағымыздың мақсаты сендерді тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және котангенсінің анықтамаларын сендерге түсіндіру және есептер шығара білуге жаттықтыру.

Осы тік бұрышты үшбұрыштың қабырғаларының қатынастарын қарастырымыз.

Алдымен а сүйір бұрышының косинусыдеген түсінікке назар аударайық.

1. Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің гипотенузаға қатынасы осы бұрыштың косинусы деп аталады.

Оны қысқаша

cos a = **** (1)

Бұл қатыныастың маңызды бір ерекшелігін атап кетейік. (1) қатынас а бұрышының шамасына тәуелді. Ол тікбұрышты үшбұрыштың қабырғаларының ұзындықтарына тәуелді емес. Демек, берілген сүйір бұрыштың косинусы бір ғана мәнге ие болады.

20 – теорема. Бұрыштың косинусы тек оның градустық өлшеміне ғана тәуелді.

Бер: Дәлелдеу:

АВС АВ сәулесіне АД = k * с,

АДЕ АС сәулесіне АЕ = k * в (k 0) өлшеп саламыз,

мұндағы АДЕ – тік бұрыш. ДЕ АЕ, керісінше

ұйғарып ДҒ ┴ АЕ деп алайық, онда АДҒ-тік

cоs α = AC = в бұрышты болады.

АВ с Д

В

Д/к cоs а = АҒ ал АДЕ:

АС АД

cоs α= ----- = α

АВ А

cоs α = АЕ = k*в = в С F Е

АД k*с c

= АЕ ал cos α= в болғандықтан AF= в сонда

с AD с

АВС: АҒ = АЕ АҒ = АЕ және cоs α = АЕ, яғни

АД АД АД АД

соs α = АЕ

АД

Теорема дәлелденді.

Тағы төмендегідей екі қатынасты анықтауға болады.

2. Анықтама: Тік бұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы сол бұрыштың с и н у с ы деп аталады.

да sin α= a/c

3. Анықтама: Тік бұрышты ұшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың т а н г е н с і деп аталады.

оны tg α=a/b

α бұрышының косинусы сияқты α бұрышының синусы да, тангенсі де сол бұрыштың градустық өлшеміне ғана тәуелді.

4. Анықтама: Тік бұрышты ұшбұрыштың сүйір бұрышына іргелес жатқан катетке қатынасы сол бұрыштың к о т а н г е н с і деп аталады.

оны ctgα=b/a

sin α , cоs α, tg α , ctg α –лар тригонометриялық өрнектер деп аталады.

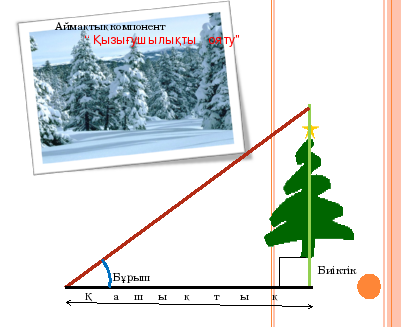
5. «Қызығушылықты ояту»аймақтық компонент. Ал осы тригонометриялық өрнектер өмірде пайдаланыла ма? Ағашқа шықпастан оның биіктігін қалай өлшеуге болады? Ол үшін ағашты тік бұрышты үшбұрыштың катеті ретіеде, ал өзіміз тұрған нүктеден ағаштың басына дейінгі екінші катет ретінде аламыз, сонда сүйір бұрышы белгілі болса ағаштың биіктігін табуға болады екен. Біздің Семейде қарағайлы орман бар. Ол дүние жүзінде 3 орын алады. Осы орманды сақтап қалу біздің борышымыз.

ІҮ.Білімді бекіту,тиянақтау/тақтамен жұмыс/ В

№125 есеп шешуі:

1. ВС=8, АВ=17 , АС=15 sin А =ВС = 8

АВ 17

т/к: sin А , cosА cosА = АС= 15 17

sin В , cosВ АВ 17 8

sin В= АС= 15

АВ 17

cosВ=ВС = 8 С 15 А

АВ 17

Жауабы: 8 , 15 , 15 , 8

17 17 17 17

Ү. «Ой толғаныс» тест жұмысы. /слайд/

Оқушыларға тапсырмалар таратылып беріледі.

Тест жұмысы

І – нұсқа

5

12

1)сos α=?

А)5 В) 12 С)13 Д)12

2 13 12 5

2)sin α=?

А)12 В) 13 С) 5 Д)5

5 12 13 12

3)tg α=?

А)5 В) 13 С)12 Д) 12

12 5 13 5

4)сtg α=?

А)13 В) 12 С) 5 Д) 13

12 5 13 5

___________________________________________________________________

1-В 2-С 3А 4В

2-нұсқа

5

β

1)сos β =?

А)3 В) 4 С) 5 Д) 3

5 5 4 4

2)sin β =?

А) 5 В) 3 С) 4 Д)5

4 5 3 3

3)tg β =?

А)5 В) 4 С) 3 Д) 4

3 3 4 5

4)сtg β =?

А)3 В) 3 С) 4 Д) 4

5 4 5 3

___________________________________________________________________

1-В 2-В 3-С 4-Д

ҮІ. Қорытынды. (слайд)

1. Тікбұрышты үшбұрыштың сүйір бұрышының синусы

2. Тікбұрышты үшбұрыштың сүйір бұрышының косинусы

3. Тікбұрышты үшбұрыштың сүйір бұрышының тангенсі

4. Тікбұрышты үшбұрыштың сүйір бұрышының котангенсі

ҮІІ. Оқушылар білімін бағалау. Бағалау парағындағы ұпайларыңды санаңдар. (слайд)

9-10 ұпай «5»

6-8 ұпай «4»

3-5 ұпай «3»

ҮІІІ. Үйге тапсырма.

8 № 125. (2) «Синус», «Косинус» сөздеріне сөзжұмбақ құрастырып келу. (слайд)