апрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерекапрырпвыарпврпв прп рпрпырвпрпрыпрваапрваекрк ерек
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
"Сан аралы?тары" 6 "А" сынып
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«"Сан аралы?тары" 6 "А" сынып»
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1400 руб.
2330 руб.
1730 руб.
2880 руб.
1340 руб.
2240 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
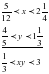 2)
2) 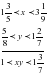 3)
3) 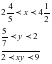 4)
4) 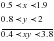
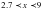 және
және 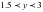
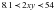 2)
2)  3)
3) 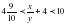
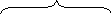

 а сан аралығы в
а сан аралығы в


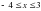 қатаң емес қос теңсіздігінің шешімдер жиынын сан аралығымен кескіндеуді қарастырайық. Теңсіздік қатаң емес болғандықтан, оның шешімдер жиынына сан аралығын көрсетіп тұрған – 4 және 3 сандары қоса енеді. Координаталық түзуде сан аралығына енетін нүкте кішкене дөңгелекпен кескінделген. Мұндай сан аралығын «кесінді» деп атайды. Белгіленуі: [ - 4;3].
қатаң емес қос теңсіздігінің шешімдер жиынын сан аралығымен кескіндеуді қарастырайық. Теңсіздік қатаң емес болғандықтан, оның шешімдер жиынына сан аралығын көрсетіп тұрған – 4 және 3 сандары қоса енеді. Координаталық түзуде сан аралығына енетін нүкте кішкене дөңгелекпен кескінделген. Мұндай сан аралығын «кесінді» деп атайды. Белгіленуі: [ - 4;3]. 
 теңсіздігінің шешімдерінің жиынын сан аралығында белгілейік. теңсіздігінің шешімдер жиынына – 2 саны енеді, бірақ 4 саны енбейді. Мұндай сан аралығы «жартылай интервал» деп аталады. Белгіленуі: [-2;4]. Оқылуы: «– 2 саны қоса алынған – 2 – ден 4 – ке дейінгі аралық».
теңсіздігінің шешімдерінің жиынын сан аралығында белгілейік. теңсіздігінің шешімдер жиынына – 2 саны енеді, бірақ 4 саны енбейді. Мұндай сан аралығы «жартылай интервал» деп аталады. Белгіленуі: [-2;4]. Оқылуы: «– 2 саны қоса алынған – 2 – ден 4 – ке дейінгі аралық». 

 теңсіздігі шешімдерінің жиынын сан аралығында белгілейік. теңсіздігі қатаң емес болғандықтан, оның шешімдер жиыны координаталық түзуде басы координатасы 8 – ге тең нүкте болатын сәулемен кескінделеді.
теңсіздігі шешімдерінің жиынын сан аралығында белгілейік. теңсіздігі қатаң емес болғандықтан, оның шешімдер жиыны координаталық түзуде басы координатасы 8 – ге тең нүкте болатын сәулемен кескінделеді. 
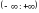 -сан түзуі д.а.
-сан түзуі д.а.