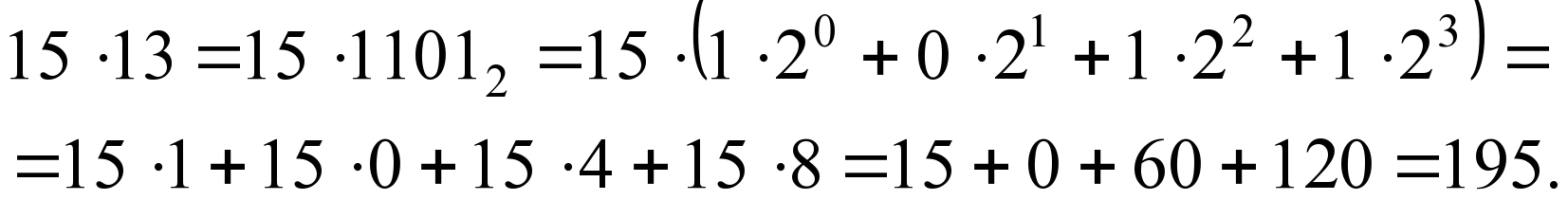А?ДАТПА
Ж?мыста б?дан 4 мы? жылдай б?рын?ы біріккен ?уатты мемлекет бол?ан ежелгі Мысыр еліні? математикасыны? т?сілдері ?арастырылады. Алдымен ежелгі Мысырда?ы арифметика тарихы беріліп, Ежелгі Мысыр т?сілімен есеп шы?аруды? ережелері (натурал сандарды к?бейту ж?не б?лу т?сілдері) келтіріледі. Мысыр т?сілі ар?ылы онды? ж?йеде берілген б?тін санды екілік санау ж?йесінде ?рнектеу ережесі беріледі.
МАЗМ?НЫ
Кіріспе
3
1
2
2.1
2.2
3
3.1
3.2
Ежелгі Мысыр математикасыны? тарихи дамуы
Ежелгі Мысыр т?сілімен есеп шы?аруды? ережелері
Ежелгі Мысыр т?сілімен сандарды к?бейту ережесі
Ежелгі Мысыр т?сілімен сандарды б?лу ережесі
Ертедегі мысырлы?тарды? ?олдан?ан есептеу ж?йелері
Мысырда?ы онды? санау ж?йесі
Мысырда?ы екілік санау ж?йесі
4
7
7
9
10
10
11
?орытынды
Пайдаланыл?ан ?дебиеттер тізімі
13
14
КІРІСПЕ
Бізді? заманымыздан 2000 жыл б?рын жазу-сызу м?дениеті г?лденген, тарих?а ?йгілі Мысыр еліні? айтулы абыздары ?осу, азайту ж?не к?бейту есептерін ал?аш рет шешкен ж?не оны ке? т?тын?ан.
Ежелгі Мысыр о?ымыстылары ?здеріні? ?ылыми е?бектерін папирустар?а жазып ?алдыр?ан. Мысырлы? математика папирустарында б?лшектерді «бірліктерге» жіктеу кестелері, кейбір геометриялы? фигураларды аудандарын ж?не к?лемдерін есептеп шы?ару ережелері, ескерткіштерді? салма?ын аны?тау?а берілген есептер, статуялар орнату ?шін ?ажетті ??рылыс материалдары мен к?н санын табу?а берілген ж?не бас?а да практикалы? есептер бар.
Натурал сандарды арифметикалы? ?осу ж?не азайту амалдары мысырлы?тарда негізінен ?азіргі кездегідей орындалатын, ал к?бейту ж?не б?луді мысырлы?тар тізбектеп екі еселеу мен ?осу?а келтіретін.
Ежелгі Мысыр т?сілімен есеп шы?аруды? ережелерін ?аза?тан шы??ан т???ыш физика-математика ?ылымдарыны? докторы, ?ла?атты ?стаз, профессор-математик, ?аза?ты? ?лтты? Академиясыны? академигі, ?аза?стан ?ылымына е?бегі сі?ген ?айраткер Орынбек Ахметбек?лы Ж?утіков ?зіні? 1969 жылы жары? к?рген математика тарихы жайында?ы е?бегінде к?рсеткен.
Зерттеу ж?мысыны? ?зектілігі:
Ежелгі Мысыр т?сілімен есеп шы?аруды? ережелерін 18 ?асыр?а дейін к?п математиктер ерекше арифметикалы? амалдар ретінде ?арастырып келді. ?азір олар арифметикалы? амалдарды? дербес жа?дайлары болып саналады. О?ушыларды? м?ндай амалдарды игеруі, оларды? математикалы? ойлау ?абілеттерін дамытады.
Зерттеуді? ма?саты мен міндеттері:
Ежелгі Мысыр т?сілімен есеп шы?аруды? ережелері ар?ылы о?ушыларды математика?а, я?ни есептеуге ?ызы?тыру.
Зерттеуді? ?дісі:
Талдау, с?хбаттасу, ба?ылау.
Зерттеуді? жа?ашылды?ы мен практикалы? ма?ыздылы?ы:
Ежелгі Мысыр т?сілімен б?тін сандарды к?бейту ж?не б?луді? ережелері игерілді, онды? санау ж?йесінде берілген сандарды екілік санау ж?йесінде ?рнектеу т?сілі берілді. Арифметикалы? амалдарды о?ушылар есеп шы?аруда ?олдана алады.
1 Ежелгі мысырда?ы математиканы? дамуы
Ежелгі Мысыр б?дан 4 мы? жылдай б?рын біріккен ?уатты мемлекет болып т?рды. Осы кезде ??рылыс аса к?шті ?ар?ынмен ж?ріп, архитектура аса ?ркендеп биік д?режеге к?теріледі, жер ?лшеу, те?ізде ж?зіп, жан-жа?пен ке?інен экономикалы?-саяси байланыс жасау ?ажеттігі к?шейеді. Мысыр пирамидалары м?ны? ай?а?ы болып табылады (1, 2-суреттер).
Сурет 1 – Ежелгі мысырда?ы пирамидалар – пер?ауындарды? мазарлары
Сурет 2 – Е? ?лкен Хеопс пирамидасы (б.э. дейінгі ІІІ?.), биіктігі 146м.
Орасан зор пирамидалар мен ?имараттарды салу ?шін, фигураларды? ?зынды?ын, ауданын, к?лемін есептей алу ?шін, ?рине, арифметиканы білу ?ажет болды. Арифметика сандармен ж?не санды (арифметикалы?) ?рнектермен айналысуды ?йретеді.
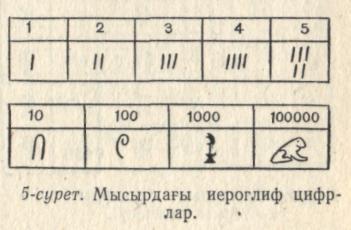
Ежелгі Мысырда б?дан 4 мы? жылдай б?рын сандарды белгілеу ?шін олар бас?а та?балар мен иероглифтерді ?олдан?ан. Бірлік ?азы?пен, онды? ?ос ?ол т?різденіп белгіленген, ж?здік б?ктелген пальма жапыра?ымен, мы? молшылы? символы ретіндегі лотос г?лімен, ж?з мы? ба?амен белгіленген, ?йткені Ніл ?зені тасы?анда ба?алар тіпті к?бейіп кететін (3, 4-суреттер).
Сурет 3 – Мысырда?ы иероглиф цифрлары
Сурет 4 – Мысырды? иероглифтік нумерациясы. 35736 саны.
Ежелгі Мысыр о?ымыстылары ?здеріні? ?ылыми е?бектерін папирустар?а жазып ?алдыр?ан. Папирус дегеніміз ежелгі Мысыр жерінде к?п ?сетін папирус деп аталатын тропиктік ірі ?сімдіктерді? саба?ынан жасал?ан аса берік те т?зімді орамдар беті, я?ни жазу материалы.
Бізді? заманымыз?а дейін са?талып келген е? к?не математикалы? папирус – Москвалы? папирус деп аталады – Москвада А.С Пушкин атында?ы музейде са?таулы, б.э. дейінгі 1850 жылы жазыл?ан папирус. Оны? ?зынды?ы 5,5 м, ал ені 8 см, онда 25 есеп келтірілген.
Мазм?ны жа?ынан аса ма?ызды папирус – Ахмес папирусы (5-сурет), Ежелгі Мысырда?ы м?ны жаз?ан хатшыны? есімімен атал?ан папирус – Лондонда Британ музейінде са?таулы. Оны? ?зынды?ы 5,5 м, ал ені 33 см. Б?л папирусты Ринд деген а?ылшын иемденген болатын, сонды?тан оны кейде Ринд папирусы деп те атайды, м?нда 85 есеп келтірілген.
Сурет 5 – Ахмес папирусыны? ?зіндісі
?алымдар са?тал?ан папирустарда?ы жазуларды аны?тап таны?аннан кейін, б?дан 4 мы? жыл б?рын?ы кезді? ?зінде мысырлы?тар онды? (біра? позициялы? емес) санау ж?йесін ?олдан?ан, сондай-а? ??рылыс, сауда ж?не ?скери істермен байланысты к?птеген есептерді шы?ара білген.
Папирустарда келтірілген есептер ?ыс?а т?рде берілген, я?ни есепті? шарты мен талабы беріледі де шешу жолы к?рсетіледі. Еш?андай д?лелдеу, тексеру жо?, барлы?ы иероглиф ар?ылы ?рнектелген с?здер мен с?йлемдерден т?рады.
4 мы? жылдай б?рын?ы мысырлы?тар жер ?лшеу, ??рылыс ж?не ?скери істеріні? ?р т?рлі есептерін те?деулер ??рып шы?ар?ан. Мысырлы?тар белгісізді «?ймек» - «Аха» деп ата?ан.
Ахмес папирусында?ы бір есеп ж?не оны шешу мысалы мынадай:
Есеп 1. ?ймек ж?не онымен 7-ні бірге ал?анда 15 болады.
Б?л есепті ?азіргіше шы?ар?анда
те?деуі ??рылады.
М?ны шешкенде табатынымыз:.
Москвалы? папирусында?ы бір есеп.
Есеп 2. Аулада 7 ?й бар. ?р ?йде 7 мысы? бар. ?р мысы? 7 тыш?ан жейді. ?р тыш?ан 7 д?н жейді. Д?ндерді? санын табу керек.
Б?л есепті? шешуі:
.
Мысырлы? математика папирустарында б?лшектерді «бірліктерге» жіктеу кестелері, кейбір геометриялы? фигураларды аудандарын ж?не к?лемдерін есептеп шы?ару ережелері, ескерткіштерді? салма?ын аны?тау?а берілген есептер, статуялар орнату ?шін ?ажетті ??рылыс материалдары мен к?н санын табу?а берілген ж?не бас?а да практикалы? есептер бар.
2 Ежелгі Мысыр т?сілімен есеп шы?аруды? ережелері
2.1 Ежелгі Мысыр т?сілімен сандарды к?бейту ережесі
Бізді? заманымыздан 2000 жыл б?рын жазу-сызу м?дениеті г?лденген, тарих?а ?йгілі Мысыр еліні? айтулы абыздары ?осу, азайту ж?не к?бейту есептерін ал?аш рет шешкен ж?не оны ке? т?тын?ан.
Натурал сандарды арифметикалы? ?осу ж?не азайту амалдары мысырлы?тарда негізінен ?азіргі кездегідей орындалатын, ал к?бейту ж?не б?луді мысырлы?тар тізбектеп екі еселеу мен ?осу?а келтіретін.
Ежелгі Мысыр т?сілімен есеп шы?аруды? ережелерін ?аза?тан шы??ан т???ыш физика-математика ?ылымдарыны? докторы, ?ла?атты ?стаз, профессор-математик, ?аза?ты? ?лтты? Академиясыны? академигі, ?аза?стан ?ылымына е?бегі сі?ген ?айраткер Орынбек Ахметбек?лы Ж?утіков ?зіні? 1969 жылы жары? к?рген математика тарихы жайында?ы е?бегінде к?рсеткен.
Ежелгі Мысыр т?сілімен сандарды к?бейту ережесін ?арастырайы?:
- Екі ?атар ба?аннан т?ратын кесте ??рамыз;
- Сол жа? ба?ан?а 1-ден бастап екі еселенген сандарды, о? жа? ба?ан?а екінші к?бейткіштен бастап екі еселенген сандарды жазамыз;
- ?рбір келесі сан алдында?ы санны? екі есесіне (?зіне-?зі ?ос?ан?а) те?;
- Сол жа? ба?анда?ы со??ы сан бірінші к?бейткіштен артпауы тиіс;
- Сол жа? ба?анда?ы сандарды? ішінен ?осындысы бірінші к?бейткішке те? болатын сандарды т?меннен жо?ары ?арай сайлап алып, соларды? т?старына к?лбеу сызы?тар ?ою керек;
- К?лбеу сызы?тар ж?ргізілген сандар?а ?арсы т?р?ан екінші ?атарда?ы сандарды ?осу керек.
Мысал 1. 3 –ті 29 –?а мысырлы?тарша к?бейту ?шін екі ?атар ба?аннан т?ратын мынадай кесте ??ру керек:
/ 1
29
/ 2
58
1 + 2 = 3
29 + 58 = 87
Мысал 2. 5 –ті 115 –ке мысырлы?тарша к?бейтейік:
/ 1
115
2
230
/ 4
460
1 + 4 = 5
460 + 115 = 575
Мысал 3. 7 –ні 79 –?а мысырлы?тарша к?бейтейік:
/ 1
79
/ 2
158
/ 4
316
4 + 2 + 1 = 7
316 + 158 + 79 = 553
Мысал 4. 13 –ті 15 –ке мысырлы?тарша к?бейтейік:
/ 1
15
2
30
/ 4
60
/ 8
120
8 + 4 + 1 = 13
120 + 60 + 15 = 195
Мысал 5. 12 –ні 18 –ге мысырлы?тарша к?бейтейік:
1
18
2
36
/ 4
72
/ 8
144
8 + 4 = 12
144 + 72 = 216
Мысал 6. К?бейтуді орында:
/ 1
34
2
68
4
136
/ 8
272
/ 16
544
16 + 8 + 1 = 25
544 + 272 + 34 = 850
Осы ?дісті к?бейткіштерді? бірі т?ра?ты болып келетін кейбір жа?дайда ?олдану ?тымды болады.
Мысалы, мынадай есепті шы?ару керек болсын:
Алыс сапар?а баратын поезд орта есеппен 57 км/са? жылдамды?пен ж?реді. Ол 8 са?атта ?андай ара ?ашы?ты?ты ж?ріп ?теді? 12; 15 са?атта ше?
Келесі кестені ??райы?:
/ 1
8
12
15
2
16
24
30
4
32
48
60
/ 8
64
96
120
/ 16
128
192
240
/ 32
256
384
480
256+128+64+8 = 456
384+192+96+12 = 684
480+240+120+15 = 855
км;
км;
км.
2.2 Ежелгі Мысыр т?сілімен сандарды б?лу ережесі
Ежелгі Мысыр т?сілімен сандарды б?лу амалы к?бейтуге кері ба?ытта келтіріледі:
- Екі ?атар ба?аннан т?ратын кесте ??рамыз;
- Сол жа? ба?ан?а 1-ден бастап екі еселенген сандарды, о? жа? ба?ан?а б?лгіштен бастап екі еселенген сандарды жазамыз;
- ?рбір келесі сан алдында?ы санны? екі есесіне (?зіне-?зі ?ос?ан?а) те?;
- О? жа? ба?анда?ы со??ы сан б?лінгіштен артпауы тиіс;
- О? жа? ба?анда?ы сандарды? ішінен ?осындысы б?лінгішке те? болатын сандарды т?меннен жо?ары ?арай сайлап алып, соларды? т?старына к?лбеу сызы?тар ?ою керек;
- К?лбеу сызы?тар ж?ргізілген сандар?а ?арсы т?р?ан сол жа? ?атарда?ы сандарды ?осу керек.
Мысал 7. Б?луді орында:
1
/ 5
2
/ 10
4
/ 20
8
40
16
80
32
/ 160
32 + 4 + 2 + 1 = 39
160 + 20 + 10 + 5 = 195
Мысал 8. Б?луді орында:
1
/ 6
2
/ 12
4
24
8
/ 48
16
/ 96
16 + 8 + 2 + 1 = 27
96 + 48 + 12 + 6 = 162
Мысал 9. Б?луді орында:
1
14
2
/ 28
4
56
8
112
16
/ 224
16 + 2 = 18
224 + 28 = 252
3 Ертедегі мысырлы?тарды? ?олдан?ан есептеу ж?йелері
3.1 Мысырда?ы онды? санау ж?йесі
Ертедегі мысырлы?тарды? ?олдан?ан есептеу ж?йесі иероглифтік онды? ж?йе бол?ан.
Он-оннан топтап санауды онды? санау ж?йесі немесе онды? нумерация деп атайды, я?ни біз он-оннан санайтынымыз белгілі: он бірліктен бір онды?, он онды?тан бір ж?здік т.с.с. ??ралады, бас?аша айт?анда: бірінші разрядты? он бірлігінен екінші разрядты? бір бірлігі, екінші разрядты? он бірлігінен ?шінші разрядты? бір бірлігі т.с.с. ??ралады. Он саны онды? санау ж?йесіні? негізі деп аталады. Олар мына т?рдегі т?йіндік сандарды та?балау ?шін арнаулы иероглифтік та?ба (6-сурет).
.
.
км;
км;
км.
түрдегі түйіндік сандарды таңбалау үшін арнаулы иероглифтік таңба (6-сурет).
, үшіншіде - 
, төртіншіде - 
тағы сол сияқты.
бүтін санды екілік есептеу жүйесінде өрнектеуге болатындығы жайлы теоремалық ой айтуға болатынын көреміз.
немесе 
