Рабочая программа по алгебре 7 класс по Ш.А.Алимову

Рабочая программа по алгебре разработана на основе ФГКОС 2004,примерной программы основного общего образования по алгебре,составитель Бурмистрова Т.А. М "Просвещение" 2011 гк мучебнику алгебры 7кл ав.Ш.А.Алимов, Колягин идр.,Москва "Просвещение" 2011г,с учётом адаптированной программы для детей с ОВЗ

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«рабочая программа по алгебре 7 класс по Ш.А.Алимову»

I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по алгебре ориентирована на учащихся 7 класса составлена на основе Примерной программы основного общего образования по алгебре 7-9, сост. Бурмистрова, Т.А. – М. Просвещение, 2011., с учетом требований федерального компонент и на основе государственного стандарта основного общего образования по математике 2004, в соответствии с авторской программой Ш.А. Алимова и адаптирована для учащихся с ОВЗ (ЗПР )Данная программа ориентирована на использование УМК Ш.А. Алимова и др.

В школе для детей с ОВЗ при изучении учебного курса ставятся те же учебно-воспитательные цели и задачи .Для учащихся с ОВЗ (характерны быстрая утомляемость, недостаточность внимания, памяти, логического мышления ,что отрицательно влияет на усвоение математических понятий в связи с этим некоторые темы будут даны в ознакомительном порядке. Для них будут использованы опорные памятки, пошаговые алгоритмы. При обучении алгебре будет продолжено использование индивидуально-дифференцированного подхода , который на основе достижения всеми обязательного уровня подготовки способствует разгрузке школьников, обеспечивает их посильной работой и формирует у них положительное отношение к учёбе.

Для достижения образовательных задач будут сочетаться традиционные и новые методы обучения, объяснительно-иллюстративные методы

Данная программа ориентирована на использование УМК Ш.А. Алимова и др.

Изучение алгебры в 7 классе направлено на достижение следующих целей:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии

2. Общая характеристика учебного предмета

Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.

При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Числа и вычисления», «Выражения и их преобразования», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики». В рамках указанных содержательных линий решаются следующие задачи:

развитие представление о числе и роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
формирование представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

3.Место предмета

Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения алгебры в 7 классе отводится 3 часа в неделю, т.е. 105 ч за год.

4.Личностные, метапредметные и предметные результаты освоения содержания курса

Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:

личностные:

сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

метапредметные:

умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково- символические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
9) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;

умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

предметные:

умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
умение решать линейные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
овладение основными способами представления и анализа статистических данных;
умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.

5.Содержание учебного предмета.

Повторение курса математики 6 класса 1ч

1. Алгебраические выражения 10 ч

Числовые выражения. Алгебраические выражения. Формулы. Свойства арифметических действий. Правила раскрытия скобок.

Основная цель — систематизировать и обобщить сведения о числовых выражениях, полученные в курсе математики 5 -6 классов; сформировать понятие алгебраического выражения, систематизировать сведения о преобразованиях алгебраических выражений, приобретенные учащимися при изучении курса математики 5-6 классов.

Первая тема курса 7 класса является связующим звеном между курсом математики 5—6 классов и курсом алгебры. При ее изучении развиваются и закрепляются вычислительные навыки, повторяются и систематизируются начальные сведения о преобразованиях выражений.

Повторяемые правила действий с рациональными числами являются основой, как для изучения данной темы, так и всего курса алгебры.

Формирование алгебраических представлений будет и в дальнейшем вестись с постоянной опорой на известные учащимся арифметические понятия, свойства, правила. В связи с этим рекомендуется первые два-три урока полностью посвятить повторению курса математики 5—6 классов, уделяя особое внимание развитию вычислительной культуры учащихся.

Через запись законов и свойств арифметических действий с помощью букв, запись формул четного и нечетного чисел и пp. осуществляется знакомство учащихся с формулами. Вплоть до изучения темы «Алгебраические дроби" принимается условная договоренность: если в формуле алгебраическое выражение записано в знаменателе, то его значение не может быть равно нулю.

При рассмотрении преобразований выражении формально-оперативные умения пока остаются на том же уровне, который был достигнут в 5-6 классах. Однако здесь учащиеся знакомятся с новым понятием алгебраической суммы, обосновывают правила раскрытия скобок соответствующими свойствами сложения и вычитания, используют свойства действий, чтобы, предварительно упростив алгебраическое выражение, найти его числовое значение.

2. Уравнения с одним неизвестным 10ч

Уравнение и его корни. Уравнения с одним неизвестным, сводящиеся к линейным. Решение задач с помощью уравнений.

Основная цель — систематизировать сведения о решении уравнений с одним неизвестным; сформировать умение решать уравнения, сводящиеся к линейным.

При изучении данной темы по сравнению с тем, что было известно учащимся ранее об уравнениях, усиливается роль теоретических знаний: вводятся определение уравнения и его корня, рассматриваются свойства уравнений, дается понятие линейного уравнения, исследуется вопрос о числе корней линейного уравнения.

Понятие равносильности уравнений на этом этапе обучения не рассматривается. Вместо этого дается пояснение того, что при решении уравнения первой степени с одним неизвестным переходят от данного уравнения к более простому, имеющему те же корни; поэтому проверку уравнения полезно делать только для того, чтобы убедиться в правильности вычислений.

Продолжается работа по формированию у учащихся умений использовать аппарат уравнений как средство для решения текстовых задач.

Одночлены и многочлены 19ч

Степень с натуральным показателем и ее свойства. Одночлен. Многочлен. Сложение, вычитание и умножение многочленов. Деление одночлена и многочлена на одночлен.

Основная цель — выработать умение выполнять действия над степенями с натуральными показателями, действия сложения, вычитания и умножения многочленов.

В данной теме дается определение степени с натуральным показателем. Понятие стандартного вида числа большего 10 и запись чисел в виде суммы разрядных слагаемых используются для иллюстрации применения понятия степени с натуральным показателем.

Впервые доказательство теоретического положения в курсе математики проводится при доказательстве свойств степени, которое осуществляется параллельно с аналогичными рассуждениями для степеней, основанием которых является число. Особое внимание следует уделить формированию навыков применения свойств степени с натуральным показателем в преобразованиях. Так как эти свойства находят применение при умножении и делении одночленов, возведении одночленов в степень, то основная нагрузка при закреплении этих навыков ложится именно на материал этого раздела.

Преобразования многочленов играют важную роль в формировании умения выполнять преобразования алгебраических выражений. Вводится понятие многочлена стандартного вида. Изучаются алгоритмы сложения, вычитания и умножения многочленов. Важно, чтобы учащиеся поняли, что при выполнении этих действий над многочленами в результате получается также многочлен. Деление многочленов и одночленов на одночлен дается в ознакомительном плане с целью пропедевтики темы «Алгебраические дроби».

Разложение многочленов на множители 13ч

Вынесение общего множителя за скобки. Способ группировки. Формулы сокращенного умножения:

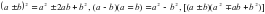Применение формул сокращённого умножения к разложению на множители.

Основная цель — выработать умения выполнять разложение многочленов на множители различными способами и применять формулы сокращенного умножения для преобразований алгебраических выражений.

При изучении данной темы рассматриваются такие способы разложения на множители, как вынесение общего множителя за скобки, группировка, использование формул сокращенного умножения. Объектом пристального внимания рекомендуется сделать темы «Способ группировки» и «Применение нескольких способов разложения на множители» как традиционно трудные, но необходимые для подготовки к изучению темы «Алгебраические дроби».

Применение разложения на множители при решении уравнений не является обязательным, так же как и изучение формул .

Формулы же (а + b)(а - b) = а2 - b2, (а ± b)2 = а2 ± 2ab + b2 должны быть усвоены учащимися и уверенно применяться ими в простейших случаях как для выполнения умножения, так и для разложения на множители.

При изучении заключительного материала темы особенно внимательно следует подойти к подбору упражнений на применение различных способов разложения многочленов на множители. Возможно ограничиться лишь выполнением упражнений обязательного уровня.

Выполнение различных упражнений на преобразования целых выражений подготавливает учащихся к изучению темы «Алгебраические дроби».

Алгебраические дроби 13ч

Алгебраическая дробь. Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. Совместные действия над алгебраическими дробями.

Основная цель - выработать умение выполнять преобразования алгебраических дробей.

Изучение темы начинается с введения понятия алгебраической дроби, ее числового значения и допустимых значений букв. Здесь же принимается важное для изучения в основной школе условие: буквы, входящие в алгебраическую дробь, принимают лишь допустимые значения.

Регулярное повторение правил действий с обыкновенными дробями существенно облегчает трудности изучения темы. Поэтому важное место в теме отводится сопоставлению алгоритмов действий над обыкновенными и алгебраическими дробями.

Важно не спешить переходить к выполнению комбинированных упражнений прежде, чем будут усвоены основные алгоритмы сложения, вычитания, умножения и деления алгебраических дробей. Не следует завышать уровень сложности упражнений на все действия с алгебраическими дробями. Соответствующие задания не должны быть излишне громоздкими и трудоемкими. Целесообразно добиваться безошибочного выполнения преобразований выражений, содержащих два-три действия.

Линейная функция и ее график 15ч

Прямоугольная система координат на плоскости. Понятие функции. Способы задания функции. График функции. Функция у = кх и ее график. Линейная функция и ее график.

Основная цель — сформировать представление о числовой функции на примере линейной функции.

Данная тема является начальным этапом в обеспечении систематической функциональной подготовки учащихся. Здесь вводятся такие понятия, как «функция», «функциональная зависимость», «независимая переменная», «график функции». Функция трактуется как зависимая переменная. Так как в 7 и 8 классах конкретные функции определены на множестве всех действительных чисел, то на данном этапе изучения функции вопрос об области ее определения в явном виде не ставится.

Рассматриваются способы задания функции. Начинается работа по формированию у учащихся умений находить значение функции, заданной формулой, графиком, по известному значению аргумента, по графику функции определять значение аргумента, если значение функции задано.

Изучению линейной функции предшествует изучение функции у = кх и ее графика. Рассматривается зависимость расположения графика функции от значений коэффициента k. Учащиеся должны понимать, как влияет знак k на расположение графика. Здесь же на физических примерах происходит первое знакомство с понятиями прямой и обратной пропорциональностей.

Построение графика линейной функции и чтение графика — важнейшие умения, необходимые учащимся для изучения как других разделов математики, так и смежных дисциплин. Формирование этих умений ведется не только при решении традиционных математических примеров, но и в процессе моделирования реальных процессов, протекающих по закону линейной зависимости.

Системы уравнений с двумя неизвестными 15 ч

Система уравнений с двумя неизвестными. Решение системы уравнений первой степени с двумя неизвестными способами подстановки и сложения, графическим способом. Решение задач методом составления систем уравнений.

Основная цель — научить решать системы линейных уравнений с двумя неизвестными различными способами и использовать полученные навыки при решении задач.

Изучение систем уравнений распределяется между курсами 7 и 8 классов. В 7 классе вводится понятие системы уравнений и рассматриваются системы линейных уравнений с двумя неизвестными.

Основное внимание при обучении решению систем уравнений уделяется способам подстановки и сложения. Графический способ используется для иллюстрации наличия или отсутствия решений системы.

Элементы комбинаторики.6 ч

Исторические комбинаторные задачи. Различные комбинации с выбором из трех элементов. Таблица вариантов. Правило произведения. Подсчет вариантов с помощью графов.

Основная цель — развить комбинаторное мышление, сформировать умение организованного перебора упорядоченных и неупорядоченных комбинаций из двух-четырех элементов.

В данной теме интегрируются арифметические, начальные алгебраические и геометрические знания учащихся. Рассматриваются исторические комбинаторные задачи, способы составления фигурных чисел, магических и латинских квадратов, выводится формула n-го треугольного числа. В ходе организованного перебора различных комбинаций элементов двух множеств обосновывается правило произведения. С его помощью решаются простейшие комбинаторные задачи.

Дополнительно приводится вывод формулы числа перестановок из n элементов, решается задача подсчета числа способов разбиения элементов выборки на две группы, проводятся рассуждения о возможности принятия или опровержения гипотезы.

Повторение. 9ч

Календарно-тематическое планирование

№ урока	№ урока в теме			Раздел, тема урока, количество часов	Основные виды учебной деятельности	Требования к результату	Виды контроля	Характеристика основных видов деятельности ученика(на уровне учебных действий)
№ урока	№ урока в теме	дата	ОВЗ	Раздел, тема урока, количество часов	Основные виды учебной деятельности	Требования к результату	Виды контроля
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 11 ЧАСОВ
1	1. 1.	01.09 3.09		Повторение.действия с десятичными и обыкновенными дробями Числовые выражения	Знакомятся с понятием «числовые выражения», применяют свойства при тождественных преобразованиях выражений.	Знать понятие числового выражения, числового равенства, действия по ступеням Уметь определять числовое выражение, определять порядок действий	Фронтальный опрос Беседа Индивидуальный опрос	Выполнять элементарные знаково-символические действия: применять буквы для обозначения чисел, для записи общих утверждений составлять выражения по условиям, заданным словесно, преобразовывать алгебраические суммы и произведения(выполнять приведение подобных слагаемых раскрытие скобок, упрощение произведений)Вычислять числовое значение буквенного выражения. Составлять формулы, выражающие зависимости между величинами ,вычислять по формулам
2	2	4.09		Алгебраические выражения	Знакомятся с понятием «алгебраические выражения», применяют свойства при тождественных преобразованиях алгебраических выражений.	Знают о допустимых и недопустимых значениях переменной в алг.выражении Умеют определять порядок действий, подставлять допустимые значения переменных в алг.выражения	Индивидуальный опрос
3	3	8.09		Алгебраические выражения	Находят значения алгебраических выражений при различных значениях переменных, сравнивать, применять свойства при вычислениях	Знать о допустимых и недопустимых значениях переменной в алг.выражении Умеют определять порядок действий, подставлять допустимые значения переменных в алг.выражениях	Взаимо-проверка Индивидуальный опрос
5	5	10.09		Алгебраические равенства.Формулы.	Знакомятся с понятием «алгебраические равенства», составляют алгебраические равенства и находят их значение	Знать что такое математическая модель Уметь составлять математическую модель реальной ситуации, используя математический язык, выбирать способ решения	Фронтальный опрос Беседа Индивидуальный опрос
6	6	11.09		Алгебраические равенства. Формулы	Знакомятся с формулами чётного и нечётного чисел и применяют их при решении задач	Знать понятие формулы Уметь решать текстовые задачи, выделяя этапы математического моделирования, проводить информационно-смысловой анализ текста, приводить примеры	Работа с опорными карточками Индивидуальный опрос
7	7	15.09	1	Входная к\р			к/р
8	8	17.09		свойства арифметических действий	Применяют свойства арифметических действий при вычислениях и тождественных преобразований выражений	Знать переместите-льный, сочетательный и распределительный законы сложения и умножения Уметь применять законы при решении и упрощении выражений	Фронтальный опрос Беседа Индивидуальный опрос
9	9	18.09		Правила раскрытия скобок	Знакомятся с понятием «алгебраическая сумма», повторяют правила раскрытия скобок	Знать правила раскрытия скобок, понятие «алг. сумма» Уметь раскрывать скобки, представлять выражение в виде алг.суммы
10	10	22.09	Работа с опорой	Правила раскрытия скобок	Выполняют преобразования выражений на основе раскрытия скобок	Знать правила раскрытия скобок, понятие «алг. сумма» Уметь раскрывать скобки, представлять выражение в виде алг.суммы	Взаимо-проверка в группах практикум
11		24.09	Работа с опорой	контрольная работа по теме ; «Алгебраические выражения»	Применяют полученные знания и умения при решении примеров и задач		к/р
Уравнения с одним неизвестным. 10 часов
12	1	25.09		Уравнение и его корни	Знакомятся с понятием уравнения, его корнями, элементами уравнения	Знать понятие уравнения и его корней Уметь определять является ли число корнем уравнения	Фронтальный опрос Беседа Индивидуальный опрос	Приводить доказательные рассуждения о корнях уравнения с опорой на определение корня, числовые свойства выражений. Распознавать линейные уравнения . Решать линейные уравнения, а также уравнения сводящиеся к ним. решать линейные уравнения и уравнения, сводящиеся к линейным с помощью основных свойств уравнений; решать простейшие уравнения с неизвестным под знаком модуля, составлять уравнение по условию текстовой задачи, переходить от словесной формулировки условия задачи к алгебраическим моделям путём составления линейного уравнения; решать составленное уравнение ,интерпретировать результат.
14	3	29.09		Уравнение и его корни	Решают уравнения используя алгоритм решения линейного уравнения	Знать алгоритм решения линейного уравнения Уметь решать линейные уравнения	Фронтальный опрос Беседа Индивидуальный опрос
15	4	1.10		Решение уравнений с одним неизвестным, сводящихся к линейным	Решают уравнения. Составляют уравнения по условию задания	Знать алгоритм решения уравнений, сводящихся к линейным Уметь выполнять преобразования и приводить уравнения к линейным	Работа с опорным материалом Индивидуальный опрос
16	5	2.10		Решение уравнений с одним неизвестным	Решают уравнения, проводят преобразования уравнений	Знать алгоритм решения уравнений, сводящихся к линейным Уметь выполнять преобразования и приводить уравнения к линейным	Взаимо-проверка в группах практикум
17	6	6.10	Ознакомит. Работа с опорными карточкам по уравнения	решение задач с помощью уравнений	Знакомятся со структурой решения текстовой задачи	Знать этапы составления математической модели задачи Умеют классифицировать текстовые задачи, строят модель и составляют уравнения	Фронтальный опрос Беседа Индивидуальный опрос
18	7	8.10	Работа с опорными карточкам по уравнения	Решение задач с помощью уравнений	«Переводят» задачу на математический язык, решают задачи «на движение»	Знать этапы составления математической модели задачи Уметь выделять условия, необходимые для решения задачи, составлять уравнение	Работа с опорными карточками Индивидуальный опрос
19 20	9	9.10 13.10		Решение упражнений по теме «Уравнения с одним неизвестным» Зачёт по теме уравнения	Решают уравнения. Составляют по условию задачи уравнение и решают задачи	Знать алгоритм решения уравнений, сводящихся клинейным Уметь решать линейные уравнения и сводящиеся к ним	Фронтальный опрос Беседа Индивидуальный опрос Индивид.задания
21	10	15.10 16.10		Контрольная работа № 2 по теме «Уравнение с одним неизвестным» Обобщение материала по теме: Уравнения.	Применяют полученные знания и умения при решении примеров и задач Решают уравнения и задачи с помощью уравнений		Индивидуальная работа
Одночлены и многочлены. 19 часов
22	1	20.10		Определение степени с натуральным показателем	Знакомятся с понятием степени числа, читают записывают степень числа	Знать определение степени числа Уметь записывать степень числа, читать выражение, содержащее степень числа	Работа с опорными карточками Индивидуальный опрос	Многочлен стандартного вида; выполнять умножение многочленов ; делить одночлен на одночлен; делить многочлен на Формулировать ,записывать в символической форме и обосновывать свойства степени с натуральным показателем, применять свойства степени для преобразования выражений и вычислений. Выполнять действия с одночленами и многочленами .Применять различные формы самоконтроля при выполнении преобразований выражений. Уметь приводить одночлены к стандартному виду; выполнять умножение одночленов и возводить одночлены в натуральную степень. Уметь называть члены многочлена; записывать все члены многочлена в стандартном виде; применять алгоритм приведения многочлена к стандартному виду; находить сумму и разность многочленов, преобразуяодночлен
23	2	22.10		Вычисление степени числа с натуральным показателем	Вычисляют степень числа с N показателем, упрощают выражения на основе определения степени числа	Знать определение степени числа Уметь проводить вычисление и упрощать выражения, содержащие степень с натуральным показателем	Фронтальный опрос Беседа Индивидуальный опрос
24	3	23.10		Свойства степени с натуральным показателем	Выводят свойства степеней с N показателем	Знать правила, выражающие свойства степени Уметь определять правило, необходимое в данному случаю	Взаимо-проверка в группах практикум
25	4	27.10		Применение свойств степени с натуральным показателем для преобразований числовых и алгебраических выражений	Преобразовывают числовые и алгебраические выражения на основе свойств степени N показателем	Знать правила, выражающие свойства степени Уметь применять данные правила для преобразования числовых и алгебраических выражений	Работа с опорными карточками Индивидуальный опрос
26	5	29.10		Применение свойств степени с натуральным показателем для упрощения вычислений	Упрощают числовые выражения, используя свойства степени N показателем	Знать правила, выражающие свойства степени Уметь применять данные правила для преобразования числовых и алгебраических выражений	Фронтальный опрос Беседа Индивидуальный опрос
27	6	30.10		Одночлен. Стандартный вид одночлена	Знакомятся с понятием «одночлен», читают, записывают одночлены. Приводят одночлены в стандартный вид	Знать определение одночлена Уметь представлять одночлен в стандартном виде	Фронтальный опрос Беседа Индивидуальный опрос
28	7	10.11		Алгоритм умножения одночленов	Знакомятся с алгоритмом умножения одночленов. Выполняют умножение одночленов по алгоритму	Знать алгоритм умножения одночленов Уметь выполнять умножение одночленов по алгоритму	Взаимо-проверка в группах практикум
29	8	12.11		Умножение одночленов	Умножают одночлены. Упрощают выражения, используя правило умножения одночленов	Знать алгоритм умножения одночленов Уметь выполнять умножение одночленов по алгоритму	Работа с опорными карточками Индивидуальный опрос
30	9	13.11		Контрольная работа № 3 по теме «Свойства степени с натуральным показателем. Одночлены»	Применяют полученные знания и умения при решении примеров и задач		Индивидуальный опрос
31	10	17.11		Многочлены	Знакомятся с понятием «многочлен», читают, записывают многочлены. Приводят многочлены в стандартный вид	Знать определение многочлена Уметь определять многочлен, записывать его и читать, приводить многочлен в стандартный вид	Фронтальный опрос Беседа Индивидуальный опрос
32	11	19.11		Приведение подобных членов	Повторяют понятие «подобные слагаемые», приводят подобные члены.	Знать, что значит привести подобные члены Уметь приводить подобные слагаемые	Взаимо-проверка в группах практикум
33	12	20.11		Сложение и вычитание многочленов	Выполняют сложение и вычитание многочленов. Упрощают выражения	Знать алгоритм сложения и вычитания многочленов Уметь выполнять операции сложения и вычитания многочленов	Работа с опорными карточками Индивидуальный опрос
34	13	24.11		Алгоритм умножения многочлена на одночлен	Умножают многочлен на одночлен. Упрощают выражения	Знать алгоритм умножения многочлена на одночлен Уметь применять алгоритм	Фронтальный опрос Беседа Индивидуальный опрос
35	14	26.11		Умножение многочлена на одночлен	Умножают многочлен на одночлен. Упрощают выражения и находят значение получившегося выражения	Знать алгоритм умножения многочлена на одночлен Уметь применять алгоритм	Фронтальный опрос Беседа Индивидуальный опрос
36	15	27.11		Алгоритм умножения многочлена на многочлен	Знакомятся с алгоритмом умножения многочлена на многочлен. Выполняют умножение по алгоритму	Знать алгоритм умножения многочлена на многочлен Уметь применять алгоритм при выполнении упражнений	Взаимо-проверка в группах практикум
37	16	1.12		Умножение многочлена на многочлен при упрощении выражений	Проводят упрощение выражений на основе правила умножения многочлена на многочлен	Знать алгоритм умножения многочлена на многочлен Уметь применять алгоритм при выполнении упражнений	Работа с опорными карточками Индивидуальный опрос
38	17	3.12		Деление одночлена на одночлен	Знакомятся с правилом деления многочлена на одночлен и многочлен	Знать алгоритм деления одночлена на одночлен Уметь применять алгоритм при выполнении упражнений	Фронтальный опрос Беседа Индивидуальный опрос
39	18	4.12		Деление многочлена на многочлен	Делят многочлены на многочлены . проводят упрощение выражений	Знать алгоритм деления многочлена на многочлен Уметь применять алгоритм при выполнении упражнений	Взаимо-проверка в группах практикум
40	19	8.12	Работа с опорой	Контрольная работа № 3 по теме «Одночлены и многочлены»	Применяют полученные знания и умения при решении примеров и задач		Индивидуальный опрос
Разложение многочленов на множители. 13 часов
41	1	10.12		Разложение многочлена на множители вынесением общего множителя за скобки	Знакомятся с задачей разложения многочлена на множители	Знать понятие разложение многочлена на множители Уметь определять, какой множитель необходимо вынести за скобки и выносить общий множитель за скобки	Фронтальный опрос Беседа Индивидуальный опрос	Доказывать формулы сокращённого умножения, применять их в преобразованиях выражений в многочлены и вычислениях. Выполнять разложение многочленов на множители с помощью формул сокращённого умножения. Решать уравнения, применять свойство равенства нулю произведения. выполнять вынесение общего множителя за скобки по алгоритму; выполнять разложение многочлена на множители способом группировки по алгоритму. Знать формулы сокращённого умножения, уметь разложить многочлен на множители различными способами. Применять различные формы самоконтроля при выполнении преобразований.
42	2	11.12		Вынесение общего множителя за скобки	Выносят общий множитель за скобки	Знать алгоритм вынесения общего множителя за скобки Уметь выносить общий множитель за скобки	Взаимо-проверка в группах практикум
43	3	15.12		Разложение на множители способом группировки	Выполняют разложение многочлена на множители способом группировки используя алгоритм	Знать алгоритм разложения на множители группировкой Уметь выполнять метод группировки многочлена, состоящего из четырёх множителей	Работа с опорными карточками Индивидуальный опрос
44	4	17.12		Разложение на множители способом группировки	Применяют для разложения на множители способ группировки	Знать алгоритм разложения на множи-тели группировкой Уметь выполнять метод группировки многочлена, состоящего из 4-х множителей	Фронтальный опрос Беседа Индивидуальный опрос
45	5	18.12		Способ группировки	Упрощают выражения и находят значение числовых выражений применяя способ группировки	Знать алгоритм разложения на множи-тели группировкой Уметь выполнять метод группировки многочлена, состоящего из 4-х множителей	Фронтальный опрос Беседа Индивидуальный опрос
46	6	22.12		Формула разности квадратов	Выводят формулу разности квадратов.	Знать формулу разности квадратов Уметь применять формулу разности квадратов	Взаимо-проверка в группах практикум
47	7	25.12	Работа с опорой на карт .разн квад.	Применение формулы разности квадратов для преобразований выражений	Раскладывают на множители, используя формулу разности квадратов	Знать формулу разности квадратов Уметь применять формулу разности квадратов в прямом и обратном виде при преобразованиях	Работа с опорными карточками Индивидуальный опрос
48	8	24.12		Квадрат суммы Квадрат разности	Выводят формулу квадрата суммы и разности двух чисел	Знать формулу квадрата суммы и разности Уметь применять формулу квадрата суммы	Фронтальный опрос Беседа Индивидуальный опрос
49	9	25.12	Работас формулами сокр умнож.	Применение формулы квадрата суммы для упрощения выражений	Упрощают выражения применяя формулу квадрата суммы	Знать формулу квадрата суммы Уметь применять формулу квадрата суммы при упрощении выражений	Фронтальный опрос Беседа Индивидуальный опрос
50	10	12.01		Применение нескольких способов разложения многочлена на множители	Представляют многочлены в виде произведения применяют одновременно несколько способов разложения на множители	Знать что означает термин «разложить многочлен на множители», способы разложения на множители Уметь определять способы и применять способы для решения	Взаимо-проверка в группах практикум
51	11	14.01	Работа с формулами	Алгоритм применения нескольких способов разложения многочлена на множители	Знакомятся с алгоритмом применения нескольких способов разложения многочлена на множители	Знать что означает термин «разложить многочлен на множители» Уметь определять способ и применять этот способ для решения	Работа с опорными карточками Индивидуальный опрос
52	12	1501		Упрощение выражений с применением нескольких способов разложения многочлена на множители	Упрощают выражения и находят их значения применяя одновременно несколько способов разложения на множители	Знать что означает термин «разложить многочлен на множители», способы разложения на множители Уметь определять способы и применять способы для решения	Фронтальный опрос Беседа Индивидуальный опрос
53	13	19.01	Работа с опорой	Контрольная работа № 4 по теме «Разложение многочленов на множители»	Применяют полученные знания и умения при решении примеров и задач		Индивидуальный опрос
Алгебраические дроби. 13 часов
54	1	21.01		Понятие алгебраической дроби. Сокращение алгебраических дробей	Знакомятся с понятием алгебраической дроби, находят значение алгебраические дроби	Знать понятие алгебраической дроби основное свойство дроби, Уметь определять алгебраическую дробь и проводить сокращение алгебраических дробей	Работа с опорными карточками Индивидуальный опрос	Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей. Выполнять действия с алгебраическими дробями. Находить допустимые значения букв ,входящих в алгебраическую дробь .Решать уравнения ,сводящиеся к линейным с дробными коэффициентами. Выполнять совместные действия над выражениями, содержащими алгебраические дроби.
55	2	22.01		Сокращение алгебраических дробей	Применяют алгоритм сокращения дробей, основное свойство дроби, сокращают дроби	Знать основное свойство дроби Уметь применять основное свойство дроби и выполнять сокращение дробей	Фронтальный опрос Беседа Индивидуальный опрос
56	3	26.01		Алгоритм приведения алгебраических дробей к общему знаменателю	Знакомятся с алгоритмом приведения алгебраических дробей к общему знаменателю и отрабатывают его при решении упражнений	Знать основное свойство дроби, понятие дополнительного множителя Уметь приводить алгебраические дроби к общему знаменателю	Взаимо-проверка в группах практикум
57	4	28		Приведение алгебраических дробей к общему знаменателю	Находят общий знаменатель двух дробей и приводят их к общему знаменателю	Знать основное свойство дроби, понятие дополнительного множителя Уметь приводить алгебраические дроби к общему знаменателю	Работа с опорными карточками Индивидуальный опрос
58	5	29.01		Алгоритм сложения и вычитания алгебраических дробей	Находят общий знаменатель двух дробей и приводят их к общему знаменателю	Знать алгоритм сложения и вычитания дробей Уметь определять общий знаменатель и выполнять сложения и вычитания дробей	Фронтальный опрос Беседа Индивидуальный опрос
59	6	5.02	Выполн.не сложных заданий	Сложение и вычитание алгебраических дробей	Находят общий знаменатель нескольких дробей и приводят их к общему знаменателю	Знать алгоритм сложения и вычитания дробей Уметь определять общий знаменатель и выполнять сложения и вычитания дробей	Взаимо-проверка в группах практикум
60	7	8.02		Сложение и вычитание алгебраических дробей	Находят общий знаменатель нескольких дробей и приводят их к общему знаменателю	Знать алгоритм сложения и вычитания дробей Уметь определять общий знаменатель и выполнять сложения и вычитания дробей	Работа с опорными карточками Индивидуальный опрос
61	8	10.02		Умножение и деление алгебраических дробей	Умножают дроби Делят дроби	Знать алгоритм умножения и деления алгебраических дробей Уметь выполнять умножение и деление	Фронтальный опрос Беседа Индивидуальный опрос
62	9	12.02		Умножение и деление алгебраических дробей	Находят значение выражений применяют правило умножения и деления дробей	Знать алгоритм умножения и деления алгебраических дробей Уметь выполнять умножение и деление	Фронтальный опрос Беседа Индивидуальный опрос
63	10	15.02		Определения порядка действий с дробями	Определяют в выражении порядок действий	Знать порядок выполнения ступеней действий Уметь определять порядок действий	Взаимо-проверка в группах практикум
64	11	17.02		Совместные действия над алгебраическими дробями	Определяют в выражении порядок действий и проводят упрощение выражений	Знать основные алгоритмы действий с алг. дробями Уметь выполнять сложение, вычитание, умножение и деление	Работа с опорными карточками Индивидуальный опрос
65	12	19.02		Совместные действия над алгебраическими дробями	Определяют в выражении порядок действий и проводят упрощение выражений	Знать основные алгоритмы действий с алг. дробями Уметь выполнять сложение, вычитание, умножение и деление	Фронтальный опрос Беседа Индивидуальный опрос
66	13	22.02		Контрольная работа № 6 по теме «Алгебраические дроби»	Применяют полученные знания и умения при решении примеров и задач		Индивидуальный опрос
Линейная функция и её график. 9 ч
67	1	24.02		Понятие функции, как зависимой переменной Способы задания функции	Знакомятся с понятием функции, аргумента функции, зависимой и независимой переменной Задают функции формулой, таблицами и графиком	Знать определение функции, аргумента функции Уметь приводить примеры функций, называть аргумент функции	Фронтальный опрос Беседа Индивидуальный опрос	Строить по точкам графики функций. Вычислять значения функций, заданными формулами .;составлять таблицы значений. Описывать свойства функций на основе её графического представления. Моделировать реальные зависимости, выражаемые линейной функцией, с помощью формул и графиков. Интерпретировать графики реальных зависимостей. Использовать функциональную символику для записи разнообразных фактов, обогащая опыт выполнения знаково-символических действий .Строить речевые конструкции с использованием функциональной терминологии. Распознавать линейную функцию. Показывать схематически положение на координатной плоскости графиков функций вида y = kx и y = kx +в в зависимости от значений коэффициента. Строить графики функций у=х. Строить график линейной функции ,описывать его свойства. Распознавать прямую и обратную пропорциональные зависимости. Решать текстовые задачина прямую и обратную зависимость.(в том числе и с констекстом из смежных дисциплин,из реальной жизни)
68	2	26.02		Функция у = kx и её график	Выражают формулой зависимость между двумя величинами	Знать формулу, выражающую зависимость уметь определять зависимость и задавать	Взаимо-проверка в группах практикум
69	3	29.02	Пошаговый алгоритм	Построение графика функции у = kx	Выполняют построение графикафункцииу = kx	Знать алгоритм построения графика функции Уметь выполнять построение графика	Работа с опорными карточками Индивидуальный опрос
70	4	2.03		Расположение графика функции у = kxв зависимости отk	Определяют положение графика функции у = kx, используя коэффициент k	Знать алгоритм построения графика функции Уметь выполнять построение графика	Фронтальный опрос Беседа Индивидуальный опрос
71	5	4.03		Понятие линейной функции	Знакомятся с линейной функцией	Знать определение линейной функции Уметь определять линейную функцию	Фронтальный опрос Беседа Индивидуальный опрос
72	6	7.03		Линейная функция и её график	Определяют является ли функция линейной	Знать определение линейной функции Уметь определять линейную функцию	Фронтальный опрос Беседа Индивидуальный опрос
73	7	9.03		Алгоритм построения графика линейной функции	Строят график линейной функции применяя алгоритм построения	Знать алгоритм построения графика линейной функции Уметь строить график линейной функции, задавая значения табличным способом	Взаимо-проверка в группах практикум
74	8	11.03		Построение графика линейной функции	Строят график линейной функции применяя алгоритм построения	Знать алгоритм построения графика линейной функции Уметь строить график линейной функции, задавая значения табличным способом	Работа с опорными карточками Индивидуальный опрос
75	9	14.03		Контрольная работа № 7 по теме «Линейная функция и её график»	Применяют полученные знания и умения при решении примеров и задач		Индивидуальный опрос
Системы двух уравнений с двумя неизвестными. 15 часов
76	1	16.03		Системы уравнений	Повторяют свойства решения уравнений, знакомятся с неопределёнными уравнениями и понятием системы уравнений с двумя неизвестными. Определяют, являются ли пара чисел решением системы	Знать понятие системы уравнений, решение системы уравнений Уметь определять, является ли пара чисел решением системы уравнений	Фронтальный опрос Беседа Индивидуальный опрос	Определять является ли пара чисел решением данного уравнения с двумя неизвестными,приводить примерырешений равнений с двумя неизвестными. Строить графики уравнений с двумя неизвестными, указанными в содержании. Находить целые решения системы путём перебора .Решать системы двух уравнений первой степени с двумя неизвестными. Решать текстовые задачи, алгебраической моделью которых является уравнение с двумя неизвестными: переходить от словесной формулировки к алгебраической модели путём составления системы уравнений :решать эту систему уравнений Использовать функционально-графические представления для решения и исследования уравнений и систем
77	2	18.03		Способ подстановки	Знакомятся со способом подстановки при решении систем	Знать алгоритм решения систем уравнений способом подстановки	Взаимо-проверка в группах практикум
78	3	30.03	Решение не сложных сист.ур.	Алгоритм решения систем уравнений с двумя неизвестными способом подстановки	Решают системы способом подстановки по алгоритму	Знать алгоритм решения систем уравнений способом подстановки Уметь решать системы способом подстановки	Карточки
79	4	1.04		Решение систем уравнений с двумя неизвестными способом подстановки	Решают системы способом подстановки по изученному алгоритму	Знать алгоритм решения систем уравнений способом подстановки Уметь решать системы способом подстановки рациональным способом	Работа с опорными карточками Индивидуальный опрос
80	5	4.04		Способ сложения	Знакомятся со способом сложения решения систем уравнений	Знать алгоритм решения способом алгебраического сложения
81	6	6.04		Алгоритм решения систем уравнений способом сложения	Решают системы способом сложения по алгоритму	Знать алгоритм решения способом алгебраического сложения Уметь решать системы способом алгебраического сложения	Карточки
82	7	8.04		Решение систем уравнений способом сложения	Решают системы способом сложения	Знать алгоритм решения способом алгебраического сложения Уметь решать системы способом алгебраического сложения	Фронтальный опрос Беседа Индивидуальный опрос
83	8	11.04		Понятие графика уравнения	Выражают у через х и строят график уравнения	Знать понятие графика функции Уметь в уравнении выражать одну переменную через другую	Карточки
84	9	13.04	Ознак.	Графический способ решения систем уравнений	Решают системы уравнений графическим способом	Знать алгоритм графического способа решения системы уравнений Уметь работать по заданному алгоритму, правильно оформлять задания	Фронтальный опрос Беседа Индивидуальный опрос
85	10	15.04	Ознаком.	Примеры решения задач с помощью систем уравнений	Рассматривают задачи, решаемые через системы уравнений	Знать как составляется математическая модель реальной ситуации Уметь выделить и записать главное в условии задачи	Взаимо-проверка в группах практикум
86	11	18.04		Алгоритм решения задач с помощью систем уравнений	Решают текстовые задачи применяя алгоритм	Знатькак составляется математическая модель реальной ситуации Уметь решать текстовые задачи с помощью систем	карточки
87	12	20.04	Решение систем уравн.способом подстан.	Решение задач с помощью систем уравнений	Решают задачи с помощью систем уравнений	Знать как составляется математическая модель реальной ситуации Уметь решать текстовые задачи с помощью систем	Работа с опорными карточками Индивидуальный опрос
88	13	22.04		Решение упражнений по теме «Системы линейных уравнений с двумя неизвестными»	Решают системы уравнений и задачи	Знать алгоритмы решения систем уравнений подстановкой, сложением и графическим Уметь выбирать рациональный способ	карточки
89	14	25.04		Контрольная работа № 8 по теме «Системы двух уравнений с двумя неизвестными	Применяют полученные знания и умения при решении примеров и задач		Индивидуальный опрос
90	15	27.04		Анализ контрольной работы	Устраняют ошибки и недочёты		Взаимо-проверка в группах практикум
Элементы комбинаторики. 6 ч
91	1	29.04		Различные комбинации из 3-х элементов	Знакомятся с понятиями «сочетание», «размещение», «перестановки» Решают задачи по алгоритму, сопоставляют предмет с окружающим миром	Знать основные понятия Уметь выполнять простейшие задачи на вычисление числа сочетаний, размещений, перестановок	Фронтальный опрос Беседа Индивидуальный опрос	Выполнять перебор всех возможных вариантов для пересчёта объектов или комбинаций объектов. Применять правило комбинаторного умножения для решения задач на нахождение числа объектов, вариантов или комбинаций.(диагонали многоугольника, рукопожатия, число кодов, шифров, ,паролей)Подсчитывать число вариантов с помощью графов.
92	2	2.05		Таблица вариантов и правило произведения	Знакомятся с правилом составления таблиц вариантов и составляют простейшие таблицы вариантов	Знают алгоритм составления таблиц вариантов Умеют составлять таблицы вариантов	Взаимо-проверка в группах практикум
93	3	4.05	Ознак.	Подсчёт вариантов с помощью графов	Знакомятся с алгоритмом решения комбинаторных задач с использованием полного графа, выполняют поиск и отбор информации	Знают алгоритм решения задач с помощью графов Умеют решать простейшие задачи с помощью графов	Фронтальный опрос Беседа Индивидуальный опрос
94	4	6.05		Методы решения комбинаторных задач	Знакомятся с разнообразием комбинаторных задач и методами их решения .Решают комбинаторные задачи	Знают основные типы задач Умеют определять тип задачи и решать простейшие задачи	Взаимо-проверка в группах практикум
95	5	9.05	Решен.неслож.комбин. зад.	Решение комбинаторных задач	Решают задачи используя таблицу вариантов, выполняют поиск и отбор информации	Знают основные типы задач Умеют определять тип задачи и решать простейшие задачи	Работа с опорными карточками Индивидуальный опрос
96	6	11.05		Решение комбинаторных задач	Решают задачи используя таблицу вариантов, выполняют поиск и отбор информации	Знают основные типы задач Умеют определять тип задачи и решать простейшие задачи	Работа с опорными карточками Индивидуальный опрос
Повторение. 9 ч
97	1	13.05		Решение линейных уравнений	Решают линейные уравнения и уравнения, сводящиеся к ним	Знать алгоритм решения Уметь решать линейные уравнени	Фронтальный опрос Индивидуальный опрос
98	2	16.05	Работа сопорн.карт.	Формулы сокращенного умножения	Повторяют формулы сокращённого умножения применяют их при решении задач	Знать формулы сокращённого умножения Уметь раскладывать при любых значениях	Фронтальный опрос Индивидуальный опрос
99	3	18.05		Итоговая контрольная работа			к/р
100	4	20.05		Разложение многочлена на множители	применяют приём вынесения общего множителя за скобки для упрощения выражений и решения уравнений	Знают способы разложения на множители Умеют их применять	Фронтальный опрос Индивидуальный опрос
101	5	23.05		Применение нескольких способов разложения на множители при упрощении выражений	Выполняют разложение многочлена на множители	Знают способы разложения на множители Умеют их применять	Взаимо-проверка в группах практикум
102	6	25.05		Алгебраические дроби	Выполняют действия с алгебраическими дробями	Знают алгоритмы действий с алгебраическими дробями Умеют их выполнять	Взаимо-проверка в группах практикум
103	7	27.05	Решен.линейныхуравн	Решение систем уравнений	Выбирают способ решения и решают системы уравнений	Знают способы решения систем уравнений Умеют решать системы уравнений	Фронтальный опрос Беседа Индивидуальный опрос
104	8	30.05		Линейная функция и её график	Выполняют построение графика линейной функции	Знают алгоритм построения прямой Умеют выполнять построение	Взаимо-проверка в группах практикум

Материально-техническое обеспечение учебного предмета

Программа для общеобразовательных учреждений (Сборник “Программы для общеобразовательных учреждений: Алгебра 7-9 кл.”/ Сост. Т.А. Бурмистрова, 2-е изд.,.- М. Просвещение, 2011г..).
Стандарт основного общего образования по математике.

(Стандарт основного общего образования по математике //Математика в школе. – 2004г,- №4, - с.4)

Базисный учебный план ОУ

Учебник «Алгебра». Учебник для 7 класса общеобразовательных учреждений. Под ред. Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова и др. – Москва «Просвещение.» 2011г

Алгебра. 7 класс: Поурочные планы (по учебнику Ш.А. Алимова и др.)/Авт.-сост.Е.Г. Лебедева – Волгоград: Учитель, 2004.
Л.Ф. Пичурина. За страницами учебника алгебры. – Москва «Просвещение», 2007.
Тематические тесты 7 класс М.В.Ткачёва Москва «Просвещение» 2010
Цифровые образовательные ресурсы

8.Планируемые результаты изучения курса алгебры 7 класса.

В результате изучения курса алгебры в 7 классе учащиеся должны

знать/понимать:

математический язык;
свойства степени с натуральным показателем;
определение одночлена и многочлена, операции над одночленами и многочленами; формулы сокращенного умножения; способы разложения на множители;
свойство сокращения дробей, приведение алгебраических дробей к общему знаменателю;
линейную функцию, ее свойства и график;
способы решения систем двух линейных уравнений с двумя переменными;

уметь:

выполнять арифметические действия, сочетая устные и письменные приемы;

составлять математическую модель при решении задач;
выполнять действия над степенями с натуральными показателями, показателем, не равным нулю, используя свойства степеней;
выполнять арифметические операции над одночленами и многочленами, раскладывать многочлены на множители, используя метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения;
выполнять основные действия с алгебраическими дробями;
решать линейные и рациональные уравнения с одной переменной;
решать несложные текстовые задачи алгебраическим методом;
строить график линейной функции, определять свойства функции по ее графику; применять графические представления при решении уравнений, систем линейных уравнений
решать системы двух линейных уравнений с двумя переменными;

решать следующие жизненно-практические задачи:

самостоятельно приобретать и применять знания в различных ситуациях;
работать в группах;
аргументировать и отстаивать свою точку зрения;
уметь слушать других
пользоваться предметным указателем инциклопедий и справочников для нахождения информации;
самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем