- Меню
- Главная
- Дошкольное образование
- Начальные классы
- Астрономия
- Биология
- География
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Естествознание
- Всемирная история
- Всеобщая история
- История России
- Право
- Окружающий мир
- Обществознание
- Экология
- Искусство
- Литература
- Музыка
- Технология (мальчики)
- Технология (девочки)
- Труд (технология)
- Физкультура
- ИЗО
- МХК
- ОБЗР (ОБЖ)
- Внеурочная работа
- ОРК
- Директору
- Завучу
- Классному руководителю
- Экономика
- Финансовая грамотность
- Психологу
- ОРКиСЭ
- Школьному библиотекарю
- Логопедия
- Коррекционная школа
- Всем учителям
- Прочее
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
- Главная
- Математика
- Планирование
- Рабочая программа по математике 5-9 класс по А.Г.Мерзляк
Рабочая программа по математике 5-9 класс по А.Г.Мерзляк
Просмотр содержимого документа
«Рабочая программа по математике 5-9 класс по А.Г.Мерзляк»
Муниципальное бюджетное общеобразовательное учреждение Шахунская средняя общеобразовательная школа №2
| СОГЛАСОВАНО | СОГЛАСОВАНО | УТВЕРЖДЕНО
|
| Протокол заседания МО учителей | Протокол заседания педагогического совета | Директор__________Масленникова Т.А. |
| от «____»________2015г. | от «____»___________2015г. | Приказ №____ |
| №___ | №___ | Дата_______________ |
| Руководитель МО: |
|
|
| ________/____________ (подпись/расшифровка подписи) |
|
|
РАБОЧАЯ ПРОГРАММА
учебного курса
«Математика»
для обучающихся 5-9 классов
(базовый уровень)
Разработали :
Масленникова Татьяна Алексеевна
(первая квалификационная категория) ,
Шлякова Галина Дмитриевна
(высшая квалификационная категория) ,
Новоженова Яна Владимировна
(первая квалификационная категория),
Николаевская Екатерина Александровна
(первая квалификационная категория).
г/о г.Шахунья
2015г.
Пояснительная записка
Рабочая программа по математике составлена на основе Федерального государственного образовательного стандарта основного общего образования, примерной программы по математике и авторской программы А.Г. Мерзляка, В.Б. Полонского, М.С. Якир, Е. В. Буцко.
Данная рабочая программа ориентирована на учащихся 5-9 классов и реализуется на основе следующих документов:
- программы по курсу математики 5–9 классов, созданной на основе единой концепции преподавания математики в средней школе, разработанной А.Г. Мерзляком, В.Б. Полонским, М.С. Якиром — авторами учебников, включённых в систему «Алгоритм успеха»;
- стандарта основного общего образования по математике;
- ООП ООО МБОУ СОШ№2
Программа соответствует учебнику «Математика» для 5-9 классов образовательных учреждений /А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко. — М. :Вентана-Граф, 2014 г.
Программа по математике составлена на основе Фундаментального ядра содержания общего образования, требований к результатам освоения образовательной программы основного общего образования, представленных в федеральном государственном стандарте основного общего образования с учётом преемственности с Примерными программами для начального общего образования по математике. В ней также учитываются доминирующие идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования, которые обеспечивают формирование российской гражданской идентичности, коммуникативных качеств личности, и способствуют формированию ключевой компетенции – умению учиться.
Курс математики 5-9 классов является фундаментом для математического образования и развития школьников, доминирующей функцией при его изучении в этом возрасте является интеллектуальное развитие учащихся. Курс построен на взвешенном соотношении новых и ранее усвоенных знаний, обязательных и дополнительных тем для изучения, а также учитывает возрастные и индивидуальные особенности усвоения знаний учащимися.
Практическая значимость школьного курса геометрии 7-9 классов состоит в том, что предметом её изучения являются пространственные формы и количественные отношения реального мира. В современном обществе математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.
Геометрия является одним из опорных школьных предметов. Геометрические знания и умения необходимы для изучения других школьных дисциплин (физика, география, химия, информатика и др.).
Одной из основных целей изучения геометрии является развитие мышления, прежде всего формирование абстрактного мышления. В процессе изучения геометрии формируются логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность. Для адаптации в современном информационном обществе важным фактором является формирование математического стиля мышления, включающего в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию.
Обучение геометрии даёт возможность школьникам научиться планировать свою деятельность, критически оценивать её, принимать самостоятельные решения, отстаивать свои взгляды и убеждения.
В процессе изучения геометрии школьники учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого выполнения математических записей, при этом использование математического языка позволяет развивать у учащихся грамотную устную и письменную речь.
Знакомство с историей развития геометрии как науки формирует у учащихся представления о геометрии как части общечеловеческой культуры.
Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, доказательство, обобщение и систематизацию. Особо акцентируются содержательное раскрытие математических понятий, толкование сущности математических методов и области их применения, демонстрация возможностей применения теоретических знаний для решения разнообразных задач прикладного характера. Осознание общего, существенного является основной базой для решения упражнений. Важно приводить детальные пояснения к решению типовых упражнений. Этим раскрывается суть метода, предлагается алгоритм или эвристическая схема решения упражнений определённого типа.
Цели курса:
Изучение математики в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
• развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении
• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении
• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Практическая значимость школьного курса математики 5-9 классов состоит в том, что предметом её изучения являются пространственные формы и количественные отношения реального мира. В современном мире математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.
Математика является одним из опорных школьных предметов. Математические знания и умения необходимы для изучения алгебры и геометрии в старших классах, а также для изучения смежных дисциплин.
Одной из основных целей изучения математики является развитие мышления, прежде всего формирования абстрактного мышления.
В процессе изучения математики также формируются и такие качества мышления, как сила и гибкость, конструктивность и критичность.
В процессе изучения математики ученики 5-9 классов учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого и грамотного выполнения математических записей, при этом использование математического языка позволяет развивать у учащихся грамотную устную и письменную речь.
Знакомство с историей развития математики как науки формирует у учащихся представления о математике как части общечеловеческой культуры.
Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, обобщение и систематизацию. Особо акцентируется содержательное раскрытие математических понятий, толкование сущности математических методов и области их применения, демонстрация возможностей применения теоретических знаний для решения задач прикладного характера, например, решение текстовых задач, денежные и процентные расчеты, умение пользоваться количественной информацией, представленной в различных формах, умение «читать» графики. Осознание общего, существенного является основной базой для решения упражнений. Важно приводить детальные пояснения к решению типовых упражнений. Этим раскрывается суть метода, подхода, предлагается алгоритм или эвристическая схема решения упражнений определенного типа.
С точки зрения воспитания творческой личности, особенно важно, чтобы в структуру мышления учащихся, кроме алгоритмических умений и навыков, которые сформулированы в стандартных правилах, формулах и алгоритмах действий, вошли эвристические приёмы как общего, так и конкретного характера. Эти приёмы, в частности, формируются при поиске решения задач высших уровней сложности. Для адаптации в современном информационном обществе важным фактором является формирование математического стиля мышления, включающее в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию.
Обучение математики даёт возможность школьникам научиться планировать свою деятельность, критически оценивать свою деятельность, принимать самостоятельные решения, отстаивать свои взгляды и убеждения.
Знакомство с историей развития математики как науки формирует у учащихся представления о математике как части общечеловеческой культуры.
Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, обобщение и систематизацию. Особо акцентируется содержательное раскрытие математических понятий, толкование сущности математических методов и области их применения, демонстрация возможностей применения теоретических знаний для решения задач прикладного характера, например, решение текстовых задач, денежные и процентные расчеты, умение пользоваться количественной информацией, представленной в различных формах, умение «читать» графики. Осознание общего, существенного является основной базой для решения упражнений. Важно приводить детальные пояснения к решению типовых упражнений. Этим раскрывается суть метода, подхода, предлагается алгоритм или эвристическая схема решения упражнений определенного типа.
Общая характеристика курса математики в 5-9 классах
Содержание математического образования в 5-9 классах представлено в виде следующих содержательных разделов: «Арифметика», «Числовые и буквенные выражения. Уравнения», «Геометрические фигуры. Измерение геометрических величин», «Элементы статистики, вероятности. Комбинаторные задачи», «Математика в историческом развитии».»,»Алгебра», «Числовые множества», «Функции», «Элементы прикладной математики», «Алгебра в историческом развитии»
Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики и смежных дисциплин, способствует развитию вычислительной культуры и логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе связано с изучением рациональных чисел: натуральных чисел, обыкновенных и десятичных дробей, положительных и отрицательных чисел.
Содержание раздела «Числовые и буквенные выражения. Уравнения» формирует знания о математическом языке. Существенная роль при этом отводится овладению формальным аппаратом буквенного исчисления. Изучение материала способствует формированию у учащихся математического аппарата решения задач с помощью уравнений.
Содержание раздела «Геометрические фигуры. Измерения геометрических величин» формирует у учащихся понятия геометрических фигур на плоскости и в пространстве, закладывает основы формирования геометрической «речи», развивает пространственное воображение и логическое мышление.
Содержание раздела «Элементы статистики, вероятности. Комбинаторные задачи» - обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности, умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор вариантов, в том числе в простейших прикладных задачах.
Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания математического образования.
Содержание раздела «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, овладение навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.
Раздел»Числовые множества» нацелен на математическое развитие учащихся, формирование у них точно, сжато и ясно излагать мысли в устной и письменной речи.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Содержание раздела «Элементы прикладной математики» раскрывают прикладное и практическое значения математики в современном мире. Материал способствует формированию умения представлять и анализировать информацию.
Раздел «Алгебра в историческом развитии» предназначается для формирования представлений о математике как части человеческойкультуры, для общего развития школьников, создания культурно- исторической среды обучения.
Цель содержания раздела «Геометрия» — развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний. Материал, относящийся к блокам «Координаты» и «Векторы», в значительной степени несет в себе межпредметные знания, которые находят применение как в различных математических дисциплинах, так и в смежных предметах.
Содержание курса геометрии в 7-9 классах представлено в виде следующих содержательных разделов: «Геометрические фигуры», «Измерение геометрических величин», «Координаты», «Векторы», «Геометрия в историческом развитии».
Содержание раздела «Геометрические фигуры» служит базой для дальнейшего изучения учащимися геометрии. Изучение материала способствует формированию у учащихся знаний о геометрической фигуре как важнейшей математической модели для описания реального мира. Главная цель данного раздела — развить у учащихся воображение и логическое мышление путём систематического изучения свойств геометрических фигур и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности с формально-логическим подходом является неотъемлемой частью геометрических знаний.
Содержание раздела «Измерение геометрических величин» расширяет и углубляет представления учащихся об измерениях длин, углов и площадей фигур, способствует формированию практических навыков, необходимых как при решении геометрических задач, так и в повседневной жизни.
Содержание разделов «Координаты», «Векторы» расширяет и углубляет представления учащихся о методе координат, развивает умение применять алгебраический аппарат при решении геометрических задач, а также задач смежных дисциплин.
Раздел «Геометрия в историческом развитии», содержание которого фрагментарно внедрено в изложение нового материала как сведения об авторах изучаемых фактов и теорем, истории их открытия, предназначен для формирования представлений о геометрии как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения.
Место курса математики в учебном плане
Базисный учебный (образовательный) план на изучение математики в5-9классах основной школы отводит 5 учебных часов в неделю в течение каждого года обучения, всего 170 часов. (5-9 классы – 5 часов в неделю, всего 850 часов). Учебное время может быть увеличено до 6 часов в неделю за счёт вариативной части Базисного плана.
Требования к результатам обучения и освоению содержания курса
Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов развития:
в личностном направлении:
1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
2) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
4) креативность мышления, инициатива, находчивость, активность при решении математических задач;
5) умение контролировать процесс и результат учебной математической деятельности;
6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
7) воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
8) ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
9) осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
10) умение контролировать процесс и результат учебной и математической деятельности;
11) критичность мышления, инициатива, находчивость, активность при решении геометрических задач;
в метапредметном направлении:
1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и пред-ставлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
6) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
7) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
8) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
9) умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
10) умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
11) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
12) умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
13) устанавливать причинно-следственные связи, проводить доказательное рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
14) умение иллюстрировать изученные понятия и свойства фигур, опровергать неверные утверждения;
15) компетентность в области использования информационно-коммуникационных технологий;
16) первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
17) умение видеть геометрическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
18) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
19) умение понимать и использовать математические средства наглядности (чертежи, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
20) умение выдвигать гипотезы при решении задачи и понимать необходимость их проверки;
в предметном направлении:
1) овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений;
4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
5) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей;
6) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
7) овладение геометрическим языком, умение использовать его для описания предметов окружающего мира; развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
8) усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
9) умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
10) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера;
11) осознание значения геометрии для повседневной жизни человека;
12) представление о геометрии как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
13) развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования;
14) владение базовым понятийным аппаратом по основным разделам содержания;
15) систематические знания о фигурах и их свойствах;
16) практически значимые геометрические умения и навыки, умение применять их к решению геометрических и негеометрических задач, а именно:
изображать фигуры на плоскости;
использовать геометрический язык для описания предметов окружающего мира;
измерять длины отрезков, величины углов, вычислять площади фигур;
распознавать и изображать равные, симметричные и подобные фигуры;
выполнять построения геометрических фигур с помощью циркуля и линейки;
читать и использовать информацию, представленную на чертежах, схемах;
проводить практические расчёты.
Планируемые (ожидаемые) результаты обучения
математики в 5-9 классах
ЛИЧНОСТНЫЕ, МЕТАПРЕДМЕТНЫЕИ ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ СОДЕРЖАНИЯ КУРСА МАТЕМАТИКИ
Изучение математики способствует формированию у учащихся личностных, метапредметных и предметных результатов обучения, соответствующих требованиям федерального государственного образовательного стандарта основного общего образования.
Личностные результаты:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать процесс и результат учебной и математической деятельности;
критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
развитие компетентности в области использования информационно-коммуникационных технологий;
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
осознание значения математики для повседневной жизни человека;
представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования;
владение базовым понятийным аппаратом по основным разделам содержания;
практически значимые математические умения и навыки, их применение к решению математических и нематематических задач, предполагающее умения:
выполнять вычисления с натуральными числами, обыкновенными и десятичными дробями, положительными и отрицательными числами;
решать текстовые задачи арифметическим способом и с помощью составления и решения уравнений;
изображать фигуры на плоскости;
использовать геометрический «язык» для описания предметов окружающего мира;
измерять длины отрезков, величины углов, вычислять площади и объёмы фигур;
распознавать и изображать равные и симметричные фигуры;
проводить несложные практические вычисления с процентами, использовать прикидку и оценку; выполнять необходимые измерения;
использовать буквенную символику для записи общих утверждений, формул, выражений, уравнений;
строить на координатной плоскости точки по заданным координатам, определять координаты точек;
читать и использовать информацию, представленную в виде таблицы, диаграммы (столбчатой или круговой), в графическом виде;
решать простейшие комбинаторные задачи перебором возможных вариантов.
Арифметика
По окончании изучения курса учащийся научится:
особенности десятичной системы счисления;
использовать понятия, связанные с делимостью натуральных чисел;
выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
сравнивать и упорядочивать рациональные числа;
выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
использовать понятия и умения, связанные с пропорциональностью величин, процентами, в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты;
анализировать графики зависимостей между величинами (расстояние, время; температура и т.п.).
Учащийся получит возможность:
познакомиться с позиционными системами счисления с основаниями, отличными от 10;
углубить и развить представления о натуральных числах и свойствах делимости;
научиться использовать приёмы, рационализирующие вычисления, приобрести навык контролировать вычисления, выбирая подходящий для ситуации способ.
Числовые и буквенные выражения. Уравнения
По окончании изучения курса учащийся научится:
выполнять операции с числовыми выражениями;
выполнять преобразования буквенных выражений (раскрытие скобок, приведение подобных слагаемых);
решать линейные уравнения, решать текстовые задачи алгебраическим методом.
Учащийся получит возможность:
развить представления о буквенных выражениях и их преобразованиях;
овладеть специальными приёмами решения уравнений, применять аппарат уравнений для решения как текстовых так и практических задач.
Геометрические фигуры.
Измерение геометрических величин
По окончании изучения курса учащийся научится:
распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры и их элементы;
строить углы, определять их градусную меру;
распознавать и изображать развёртки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;
определять по линейным размерам развёртки фигуры линейные размеры самой фигуры и наоборот;
вычислять объём прямоугольного параллелепипеда и куба.
Учащийся получит возможность:
научиться вычислять объём пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;
углубить и развить представления о пространственных геометрических фигурах;
научиться применять понятие развёртки для выполнения практических расчётов.
Элементы статистики, вероятности. Комбинаторные задачи
По окончании изучения курса учащийся научится:
использовать простейшие способы представления и анализа статистических данных;
решать комбинаторные задачи на нахождение количества объектов или комбинаций.
Учащийся получит возможность:
приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы;
научиться некоторым специальным приемам решения комбинаторных задач.
Наглядная геометрия
Выпускник научится:
• распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;
• распознавать развёртки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;
• строить развёртки куба и прямоугольного параллелепипеда;
• определять по линейным размерам развёртки фигуры линейные размеры самой фигуры и наоборот;
• вычислять объём прямоугольного параллелепипеда.
Выпускник получит возможность:
• научиться вычислять объёмы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов.
Натуральные числа. Дроби. Рациональные числа
Выпускник научится:
• понимать особенности десятичной системы счисления;
• оперировать понятиями, связанными с делимостью натуральных чисел;
• выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
• сравнивать и упорядочивать рациональные числа;
• выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
• использовать понятия и умения, связанные с пропорциональностью величин, процентами, в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.
Выпускник получит возможность:
• познакомиться с позиционными системами счисления с основаниями, отличными от 10;
• углубить и развить представления о натуральных числах и свойствах делимости;
• научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
Действительные числа
Выпускник научится:
• использовать начальные представления о множестве действительных чисел;
• оперировать понятием квадратного корня, применять его в вычислениях.
Выпускник получит возможность:
• развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике;
• развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
Измерения, приближения, оценки
Выпускник научится:
• использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Выпускник получит возможность:
• понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
• понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.
Алгебраические выражения
Выпускник научится:
• оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
• выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
• выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;
• выполнять разложение многочленов на множители.
Выпускник получит возможность научиться:
• выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
• применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).
Уравнения
Выпускник научится:
• решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;
• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
• применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Выпускник получит возможность:
• овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
• применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
Неравенства
Выпускник научится:
• понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
• решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
• применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность научиться:
• разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
• применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
Основные понятия. Числовые функции
Выпускник научится:
• понимать и использовать функциональные понятия и язык (термины, символические обозначения);
• строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
• понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Выпускник получит возможность научиться:
• проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
• использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
Числовые последовательности
Выпускник научится:
• понимать и использовать язык последовательностей (термины, символические обозначения);
• применять формулы, связанные с арифметической и геометрической прогрессией, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.
Выпускник получит возможность научиться:
• решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессии, применяя при этом аппарат уравнений и неравенств;
• понимать арифметическую и геометрическую прогрессию как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.
Описательная статистика
Выпускник научится использовать простейшие способы представления и анализа статистических данных.
Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
Случайные события и вероятность
Выпускник научится находить относительную частоту и вероятность случайного события.
Выпускник получит возможность приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов.
Комбинаторика
Выпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Геометрические фигуры
Выпускник научится:
• пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
• распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
• находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 0° до 180°, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, подобие, симметрии, поворот, параллельный перенос);
• оперировать с начальными понятиями тригонометрии и выполнять элементарные операции над функциями углов;
• решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств;
• решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;
• решать простейшие планиметрические задачи в пространстве.
Выпускник получит возможность:
• овладеть методами решения задач на вычисления и доказательства: методом от противного, методом подобия, методом перебора вариантов и методом геометрических мест точек;
• приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении геометрических задач;
• овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки:анализ, построение, доказательство и исследование;
• научиться решать задачи на построение методом геометрического места точеки ,методом подобия;
• приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных программ;
• приобрести опыт выполнения проектов по темам «Геометрические преобразования на плоскости», «Построение отрезков по формуле».
Измерение геометрических величин
Выпускник научится:
• использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, длины окружности, длины дуги окружности, градусной меры угла;
• вычислять площади треугольников, прямоугольников, параллелограммов, трапеций, кругов и секторов;
• вычислять длину окружности, длину дуги окружности;
• вычислять длины линейных элементов фигур и их углы, используя формулы длины окружности и длины дуги окружности, формулы площадей фигур;
• решать задачи на доказательство с использованием формул длины окружности и длины дуги окружности, формул площадей фигур;
• решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).
Выпускник получит возможность научиться:
• вычислять площади фигур, составленных из двух или более прямоугольников, параллелограммов, треугольников, круга и сектора;
• вычислять площади многоугольников, используя отношения равновеликости и равносоставленности;
• применять алгебраический и тригонометрический аппарат и идеи движения при решении задач на вычисление площадей многоугольников.
Координаты
Выпускник научится:
• вычислять длину отрезка по координатам его концов; вычислять координаты середины отрезка;
• использовать координатный метод для изучения свойств прямых и окружностей.
Выпускник получит возможность:
• овладеть координатным методом решения задач на вычисления и доказательства;
• приобрести опыт использования компьютерных программ для анализа частных случаев взаимного расположения окружностей и прямых;
• приобрести опыт выполнения проектов на тему «Применение координатного метода при решении задач на вычисления и доказательства».
Векторы
Выпускник научится:
• оперировать с векторами: находить сумму и разность двух векторов, заданных геометрически, находить вектор, равный произведению заданного вектора на число;
• находить для векторов, заданных координатами: длину вектора, координаты суммы и разности двух и более векторов, координаты произведения вектора на число, применяя при необходимости сочетательный, переместительный и распределительный законы;
• вычислять скалярное произведение векторов, находить угол между векторами, устанавливать перпендикулярность прямых.
Выпускник получит возможность:
• овладеть векторным методом для решения задач на вычисления и доказательства;
• приобрести опыт выполнения проектов на тему «применение векторного метода при решении задач на вычисления и доказательства».
Требования к уровню подготовки выпускников
В результате изучения курса математики ученик должен знать/ понимать:
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Арифметика
Уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь – в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближенные числа с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
Уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координата точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составление формул, выражающих зависимость между реальными величинами; нахождения нужной формулы в справочных материала;
моделирование практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Геометрия
Уметь
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов); в том числе: для углов от 00 до 1800 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения тригонометрических задач с использованием тригонометрии;
решение практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построение геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Элементы логики, комбинаторики, статистики и теории вероятностей
Уметь
Проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и использованием правил умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве и в диалоге;
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
ОЦЕНКА УСТНЫХ ОТВЕТОВ ОБУЧАЮЩИХСЯ ПО МАТЕМАТИКЕ
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при отработке умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке обучающихся»);
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
ОЦЕНКА ПИСЬМЕННЫХ КОНТРОЛЬНЫХ РАБОТ ОБУЧАЮЩИХСЯ ПО МАТЕМАТИКЕ
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
ОБЩАЯ КЛАССИФИКАЦИЯ ОШИБОК
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
единая шкалА Критериев оценивания работы в группе
| Кол-во баллов | Критерии оценивания | |||
| Активность | Сотрудничество | Высказывание своей позиции | Поведение | |
| 0 | Не выполнено | |||
| 1 | Ученик участвует в работе группы, но не проявляет инициативы, занимает пассивную позицию | Пассивно относится к распределению и выполнению своих обязанностей в работе группы; безответственно относится к работе в команде (не может спокойно выслушать, часто перебивает и/или навязывает свою точку зрения; не оказывает помощи другим) | Высказывает свое мнение; высказывание не всегда адекватно цели, содержательно, конкретно, логично или вообще не высказывает свое мнение | При выполнении задания ученик мешает работе группы, или других групп, отвлекает от выполнения задания, нарушает дисциплину (выкрикивает с места и др.) создает конфликтные ситуации (возможно наличие неразрешенных конфликтов) |
| 2 | Участвует в работе ситуативно (время от времени); положительно влияет на успешное выполнения задания | Участвует в распределении обязанностей в группе и выполняет свои обязанности; не всегда учитывает мнения других | Высказывает свое мнение по обсуждаемому вопросу, высказывания не всегда логичны, содержательны, корректны; не всегда слушает высказывания товарищей, задает вопросы на уточнение и понимание | Ученик работает в группе, сосредоточившись на поставленном учебном задании (не отвлекая других); не нарушает дисциплину (индивидуально выполняет свою часть задания; возможно наличие разрешенного конфликта) |
| 3 | Активно работает в группе
| Ответственно относится к работе в группе; сотрудничает | Высказывает свое мнение, высказывания логичны, содержательны, корректны; считается с мнением группы; способен дать оценку группы, выступить от имени группы | Ученик выполняет задание, помогает участникам своей группы в выполнении (не отвлекая других / другие группы); не нарушает дисциплину, не создает конфликтных ситуаций |
Единая шкала критериев оценки исследования (исследовательской работы)
| Кол-во баллов | Критерии оценивания |
| ||||
| Аппарат исследования, | Содержание и полнота | Структура и оформление результатов | Грамотность и методика исследования | Публичное | ||
| 0 | Задание не выполнено | |||||
| 1–2 | Ученик выполнил задание. С помощью учителя поставлена проблема, определена тема, выявлены противоречия, сформулирована цель и задачи исследования; выводы не соответствуют поставленным задачам исследования; следует плану предложенным учителем; низкая доля самостоятельности в реализации работы на всех этапах исследования | Проведенное исследование не раскрывает тему, проблему и / или не носит исследовательского характера, оригинальные идеи отсутствуют или принадлежат научному руководителю. Ученик использует источники предложенные учителем или неадекватно их подбирает | Учеником не выдержана структура работы и / или плохо упорядочена, оформление работы не соответствует формальным требованиям и требуемому объему культура оформления | Ученик допустил значительное количество орфографических и синтактических ошибок, стилистических погрешностей (не соблюден научный стиль изложения), наличие опечаток, сокращений. Методика исследования плохо прописана, личный вклад автора в разработку средств, методов незначителен (заимствован или разработан учителем) и / или результаты исследования описаны при помощи учителя | Ученик при публичном представлении не использовал никаких наглядно-иллюстративных средств, плохо выстроил логику выступления, не смог сформулировать вывод исследования, не смог ответить на дополнительные вопросы (и / или не уложился в регламент выступления) | |
| 3–4 | Ученик справился с заданием. Самостоятельно или при небольшой помощи учителя определил тему, проблему, выявил противоречия, сформулировал цель и задачи исследования (имеются незначительные неточности, замечания); в заключении выводы не до конца отвечают на поставленные задачи; большая доля самостоятельности в реализации на всех этапах исследования | Проведенное исследование не до конца раскрывает проблему, носит исследовательский характер, имеются собственные оригинальные идеи. Ученик при незначительной помощи учителя подобрал подборку первоисточников касающиеся темы исследования | Учеником не до конца выдержана структура исследования и его оформление, текст разделен на смысловые части. Объем слегка больше или меньше требуемого. Ссылки и цитаты не все корректно оформлены | Ученик допустил незначительное количество грамматических ошибок и / или стилистических погрешностей. Методика исследования не достаточно хорошо прописана, личный вклад автора в разработку средств и методов исследования более половины (адаптирована или создана при помощи учителя); зафиксировал результаты наблюдений, исследования с использованием различных инструментов, приборов, аппаратов и др. В исследовании нет инновационных подходов и методов решения проблемы, или плохо аргументированы | Ученик не адекватно применил наглядно-иллюстративные средства, допустил нарушения в логике выступления, ответил на все дополнительные вопросы, хотя были не точности в ответах, и аргументации (даны неполные ответы), соблюден регламент | |
| 5–6 | Ученик справился с заданием. Проявил творческий подход к выбору темы исследования, самостоятельно разработал научный аппарат исследования; выводы полностью раскрывают содержание поставленных целей и задач исследования; высокая доля самостоятельности в реализации работы на всех этапах исследования | Проведенное исследование полностью раскрывает проблему, имеет исследовательский характер (результат был не очевиден до его проведения), оригинальные идеи значительны. Ученик самостоятельно нашел и использовал (обработал) большой объем источников по теме | Ученик полностью выдержал структуру исследовательской работы, прослеживается логика рассуждений при переходе от одной части к другой, оформление соответствует формальным требованиям, правильное оформление ссылок и цитат, соблюден необходимый объем работы. Высокая культура оформления | Ученик не допустил грамматических ошибок и стилистических погрешностей (соблюден научный стиль изложения); логичность, четкость и последовательность изложения информации. Методика исследования хорошо прописана, самостоятельно разработана или при небольшой поддержки учителя; ученик самостоятельно зафиксировал результаты наблюдений, опросов, анкетирования и др., используя рисунки, пояснения, таблицы, графики, диаграммы и т.д. Исследование содержит различные инновационные подходы и методы решения проблемы (хорошо аргументированы предлагаемые методы решения проблемы) | Ученик выстроил логику выступления, оптимально использовал наглядно-иллюстративные средства раскрывающие тему, четко и лаконично ответил на все заданные вопросы, соблюден регламент | |
Единая шкала критериев оценки карты самостоятельной работы ОБучаЮщихся
| Кол-во | Критерии оценивания самостоятельной работы | ||
| Срочность выполнения | Качество выполненного | Полнота | |
| 0 | Задание не выполнено | ||
| 1 | Ученик выполнил задание не | Ученик допустил неточности в выполнении задания, не раскрыта тема задания, неправильно подобран материал или полностью заимствован с литературы, Интернета, не систематизирован, не нагляден | Задание выполнено не полностью |
| 2 | Ученик выполнил задание, но с небольшим опозданием | Учеником допущены незначительные неточности в выполнении задания, тема не до конца раскрыта, слабо систематизирован материал, представлено наглядно | Задание выполнено (с небольшими замечаниями) |
| 3 | Ученик выполнил задание в срок | Учеником раскрыта тема задания, успешно подобран материал, систематизирована в искомую в соответствии с заданием, представлена наглядно | Задание выполнено полностью |
Единая шкала критериев оценки портфолио по предмету
|
Кол-во баллов | Критерии оценивания |
| ||||
| Содержание и полнота | Структура и оформление | Рефлексия | Презентация портфолио | Ответы на вопросы | ||
| 0 | Задание не выполнено | |||||
| 1–2 | По содержанию портфолио трудно судить об уровне сформированности компетенций, об усилиях приложенных в процессе выполнения работ, достижений учащихся: представлены отрывочные или незаконченные работы (не исправлены замечания, ошибки указанные учителем в карте самостоятельной работы), наличие не всех обязательных заданий (рубрик) | Учеником не выдержана структура портфолио и / или плохо упорядочена, оформление работы не соответствует формальным требованиям (неаккуратно, небрежно, ненаглядно оформлена). Низкая культура оформления | Ученик осуществляет рефлексию своей деятельности формально или не проводит совсем. Нет самооценки выполненных заданий, допущенных недочетов и путей их устранения и / или неадекватная оценка себя, своей деятельности
| Ученик демонстрирует неумение и / или нежелание самопрезентовать свои достижения | Ученик не смог ответить на заданные вопросы одноклассников, учителя | |
| 3–4 | Содержание портфолио демонстрирует уровень сформированности компетенций ученика: устранены не все замечания, рекомендации, данные учителем в карте самостоятельной работы; наличие всех обязательных заданий (рубрик) | Учеником не до конца выдержана структура портфолио, материал упорядочен; в оформлении нет или допущены незначительные нарушения, (недостаточно выражена оригинальность в оформлении) | Ученик осознает свои недостатки в работе – планирует деятельность по их устранению. Наличие самооценки, анализа своих затруднений, демонстрация динамики личностного роста | Ученик демонстрирует способность самопрезентовать свои достижения; соблюдена культура представления, но допустил нарушения в логике выступления; не до конца раскрыта суть, содержание портфолио; не адекватно применил наглядно-иллюстративные средства; соблюден регламент | Ученик ответил на все заданные вопросы одноклассников, учителя (даны неполные ответы) | |
| 5–6 | Содержание портфолио свидетельствует о больших приложенных усилиях и прогрессе учащегося | Ученик полностью выдержал структуру портфолио, материал структурирован, упорядочен; оформление соответствует формальным требованиям, проявлена оригинальность, творчество. Высокая культура оформления | Ученик проводит самооценку и рефлексию своей деятельности, способствующей к самореализации, самосовершенствованию. Проведен рефлексивный анализ своих достижений и трудностей с которыми столкнулись при выполнении заданий, определены пути их устранения, раскрыта динамика личностного роста | Ученик демонстрирует умение самопрезентовать себя, свои достижения; соблюдена культура представления: композиция речи, убедительность, аргументированность; отражены цели работы, их реализация, основные достижения, содержание работ; выстроил логику выступления, оптимально использовал наглядно-иллюстративные средства раскрывающие тему; соблюден регламент | Ученик четко и лаконично ответил на все заданные вопросы | |
Единая шкала критериев оценки проектов
|
Кол-во | Критерии оценивания |
| ||||
| Актуальность проекта, | Теоретическое | Структура и оформление | Грамотность и методика | Презентация проекта | ||
| 0 | Задание не выполнено | |||||
| 1–2 | Ученик выполнил задание. | В проекте нет полного теоретического обоснования всех положений, концепций; работа не имеет практической значимости или не описана. Новые научные результаты отсутствуют или принадлежат научному руководителю | Учеником не выдержана структура работы и / или плохо упорядочена, оформление работы не соответствует формальным требованиям и требуемому объему (слишком велик или мал). Некорректное оформление сносок, ссылок на используемую литературу или их отсутствие. Низкая культура оформления | Ученик допустил значительное количество орфографических и синтактических ошибок, стилистических погрешностей (не соблюден научный стиль изложения), наличие опечаток, сокращений. Плохо разработаны критерии и показатели реализации проекта, методы их диагностики; личный вклад автора в разработку средств, методов незначителен (заимствован или разработан учителем); результаты описаны при значительной помощи учителя | Ученик при презентации не использовал никаких наглядно-иллюстративных средств, плохо выстроил логику выступления, не смог ответить на дополнительные вопросы | |
| 3–4 | Ученик справился с заданием. Самостоятельно или при небольшой помощи учителя определил проблему, сформулировал цель и задачи проекта (имеются незначительные неточности, замечания), выбрана тематика по актуальным, перспективным направлениям, имеются собственные оригинальные идеи; большая доля самостоятельности в реализации на всех этапах проекта | В проекте не до конца дано теоретическое обоснование всех положений проекта, продукт проекта имеет небольшую значимость для решения отдельных практических задач (может быть использована в учебных целях) | Учеником не до конца выдержана структура проекта и его оформление, текст разделен на смысловые части. Объем слегка больше или меньше требуемого. Ссылки и цитаты не все корректно оформлены | Ученик допустил незначительное количество грамматических ошибок и / или стилистических погрешностей. Достаточно хорошо разработаны критерии и показатели реализации проекта, методы их диагностики, есть неточности; личный вклад автора в разработку средств и методов исследования более половины (адаптирована или создана при помощи учителя); результаты описаны при незначительной помощи учителя или самостоятельно | Ученик не адекватно применил наглядно-иллюстративные средства, допустил нарушения в логике выступления, ответил на все дополнительные вопросы, хотя были не точности в ответах, и аргументации (даны неполные ответы), соблюден регламент | |
| 5–6 | Ученик справился с заданием. Самостоятельно или при небольшой помощи учителя определил проблему, верно определил цель (способствующая решению проблемы, диагностична), задачи взаимосвязаны, обеспечивают достижение цели, выбрана тематика по актуальным и перспективным направлениям и имеющая практическое применение, оригинальные идеи значительны. Высокая доля самостоятельности в реализации работы на всех этапах проекта | В проекте представлена информация об объекте проектирования, дано теоретическое обоснование всех положений проекта, продукт имеет значимость для решения отдельных практических задач. Новые научные результаты принадлежат учащемуся и их значимость значительна | Ученик полностью выдержал структуру проекта, прослеживается логика рассуждений при переходе от одной части к другой, оформление соответствует формальным требованиям, правильное оформление ссылок и цитат, соблюден необходимый объем работы. Высокая культура оформления | Ученик не допустил грамматических ошибок и стилистических погрешностей (соблюден научный стиль изложения); логичность, четкость и последовательность изложения информации. Представлены ожидаемые результаты от реализации проекта, критерии и показатели, методы их диагностики. Методика исследования хорошо прописана, самостоятельно разработана или при небольшой поддержки учителя | Ученик выстроил логику выступления, оптимально использовал наглядно-иллюстративные средства раскрывающие тему, четко и лаконично ответил на все заданные вопросы, соблюден регламент, речь выступающего соответствует правилам публичного выступления | |
Единая шкала критериев оценки электронной презентации
| Кол-во баллов | Критерии оценивания | |||
| Полнота освещения вопроса | Качество презентации | Умение отвечать на вопросы: лаконичность и аргументированность | Дизайн презентации | |
| 0 | Электронная презентация не выполнена | |||
| 1 | Ученик или группа учащихся выполнили задание, тема не раскрыта, материал не систематизирован, не выстроена логика презентации | Регламент презентации не соблюден, информация, изложенная в презентации не соответствует обозначенной теме, переизбыток или недостаток текстовой информации, полностью заимствованная с литературы, Интернета | Ученик не смог ответить на вопросы | Иллюстрации низкого качества, отсутствует необходимые таблицы, схемы графики, эффекты примененные в презентации отвлекают от содержания |
| 2 | Ученик или группа учащихся создали презентацию, тема творческого задания не до конца раскрыта, имеются незначительные неточности, слабая систематизации информации, есть нарушения в логике презентации | Немного нарушен регламент презентации, информация по проблеме изложена не полностью, присутствуют незначительные недочеты, использованы различные источники информации, материал проанализирован | Ученик ответил на все вопросы, хотя были не точности в ответах, и аргументации | Иллюстрации хорошего качества, подобранна соответствующая графическая информация, примененные эффекты немного мешают усвоению информации |
| 3 | Ученик или группа учащихся справились с заданием, тема раскрыта, успешно извлечена информация, систематизирована, выстроена логика презентации | Презентация разработана самими учащимися, регламент не нарушен, информация изложена полно и чет- ко, текст на слайде представляет собой опорный конспект, отсутствует переизбыток информации | Ученик четко и лаконично ответил на все заданные вопросы | Дизайн презентации четко продуман, примененные эффекты помогают усвоению информации, не отвлекают внимание |
Единые критерии оценки активности ОБучаЮщихся
на уроке
3 балла – систематически (на протяжении всего урока) проявлял активность: участвовал в процессе постановке цели урока, правильно отвечал на вопросы учителя, задавал вопросы; был активно вовлечён в познавательную деятельность, участвовал в работе группы, подводил итоги рефлексию урока и т. д.;
2 балла ситуативно проявлял активность на занятии (на отдельных этапах урока); был вовлечен в познавательную деятельность, участвовал в работе группы и т. д.;
1 балл – эпизодическая активность (пассивность, созерцательный познавательный интерес); присутствовал на уроке, слушал, смотрел, записывал под диктовку учителя, переписывал с доски;
0 баллов – отсутствовал.
Мониторинг ключевых компетенций у обучающихся
| Показатели | 1 балл | 2 балла | 3 балла |
| Информационная компетенция | |||
| Планирование информационного поиска
| Слабо развиты умения определения недостающей информации, определения источника недостающей информации, планирования информационного поиска | Способен определить какой информации не хватает для решения задания, и определить ее источник | Самостоятельно определяет стратегию поиска необходимой недостающей информации и его источник |
| Поиск информации в сети Интернет | Слабо развиты умения поиска информации в сети Интернет. Испытывает затруднения в определении индикаторов поиска информации в соответствии с поставленной целью | Определяет индикаторы поиска информации в соответствии с поставленной задачей | Моделирует множество индикаторов поиска информации, используя расширенные параметры поисковых систем |
| Извлечение информации | Слабо развиты умения извлечения наиболее значимой информации из текста, выделения главного | Способен извлечь необходимую информацию из нескольких источников, и/или большого объема | Умеет извлекать наиболее значимую информацию из текста, из наглядного материала: карты, таблицы, графики, диаграммы и др. |
| Преобразование информации в другие формы | Испытывает затруднения преобразования информации из одного вида в другой | Умеет преобразовать информацию из одного вида в другой в соответствии с требованием задачи | Умеет представлять информацию в наиболее эффективном виде исходя из поставленных задач |
| Систематизация информации | Испытывает затруднение в систематизации информации в соответствии с требованием задания, может допускать ошибки в подборе, систематизации материала | Способен систематизировать информацию в соответствии с требованием задания, но допускает незначительные неточности в выполнении задания, слабо систематизирует материал | Умеет систематизировать, преобразовать и адаптировать полученную информацию требованием задания |
| Использование современных компьютерных технологий при работе с информацией | Испытывает затруднения при обработке информации с использованием современных компьютерных технологий: создание теста, графиков, таблиц, схем и др., компьютерных презентаций | Способен использовать современные технологии при работе с информацией, но нуждается в поддержке учителя | Умеет использовать современные технологии при работе с информацией, создавать электронные презентации, схемы, графики, таблицы, диаграммы и др. |
| Публичное представление своих результатов с использованием компьютерных технологий | Затрудняется в публичном представлении своих результатов с использованием компьютерных средств и технологий | Демонстрация своих результатов с использованием компьютерных средств и технологий с помощью учителя (большой объем работы делает учитель) | Публично демонстрирует результаты своих исследований с использованием компьютерных средств и технологий (самостоятельно или при незначительной помощи учителя) |
| Коммуникативная компетенция | |||
| Устная коммуникация | Монологическая и диалогическая речь развита на низком уровне, слабое владение терминологическим «языком предмета» | Монологическая и диалогическая речь развита на хорошем уровне, допускает ошибки при использовании «языка предмета» | Развитая монологическая и диалогическая речь, умение грамотно пользоваться «языком предмета» |
| Письменная коммуникация | Испытывает затруднения в оформлении своих мыслей в письменный текст: объем работы не соответствует требуемому (слишком велик или мал); при изложении допускает существенные отступления от темы; допускает грубые грамматические ошибки; не всегда обосновывает свои тезисы; некорректно оформляет ссылки и цитаты; не до конца раскрывает тему | Соблюдает нормы оформления текста заданные образцом, требованиями. При этом объем работы может быть слегка больше или меньше требуемого. При изложении допускает незначительные отступления от темы, допускает незначительное количество грамматических ошибок. Приведенные примеры не всегда уместны и убедительны, ссылки и цитаты не всегда корректно оформлены. Тема раскрыта с небольшими замечаниями | Умеет представлять результаты в письменной нерегламентированной форме, определяет жанр и структуру письменного документа в соответствии с поставленной целью. При изложении мыслей полностью придерживается темы, не допуская грубых грамматических ошибок. В подтверждении своих тезисов подкрепляет убедительными примерами, фактами. Грамотно использует первоисточники, корректно ставя ссылки и цитаты. Тема раскрыта полностью |
| Презентация результатов своей деятельности | Затрудняется в публичном представлении своих результатов | Способен к публичному представлению результатов своей деятельности, но испытывает затруднения в выборе формы, способа и в выстраивании логики выступления | Умеет публично представить результаты своей собственной деятельности, выбрать способ или форму, выстроив логику выступления, адекватно подобрав наглядные средства
|
| Продуктивная групповая коммуникация | Участвует в работе группы, но не проявляет инициативы, чаще занимает пассивную позицию или высказывает свое мнение только по ситуации | Участвует в групповой работе, высказывает свое мнение, слушает высказывания товарищей, задает вопросы на уточнение и понимание; положительно влияет на успешное выполнение задания. Способен к сотрудничеству и работе в группе | Активно работает в группе, выступает с инициативой, высказывает свое мнение, считается с мнениями группы. Сотрудничает в совместном решении проблем. Способен организовать деятельность группы на успешное выполнение задания, распределить работу среди членов группы, координировать ход выполнения задания, дать оценку группы и ее участников, выступать от имени группы |
| Участие в дискуссии / дебатах | Затрудняется высказать свою позицию. Высказывание не всегда адекватно цели, содержательно, конкретно, логично. Не умеет отстаивать свое мнение | Способен отстаивать свое мнение по обсуждаемому вопросу, но не всегда может подтвердить его доказательствами или сделать выводы. Высказывания не всегда логичны, содержательны, конкретны | Умеет делать выводы, подводить итоги обсуждения, заявлять свою позицию, формулировать и аргументированно отстаивать свою точку зрения. Высказывания логичны, содержательны, конкретны |
| Выполнение различных социальных ролей | Испытывает затруднения с выполнением заданий, где необходимо взять на себя социальной роль или от имени которого необходимо решить задание | Способен к выполнению различных заданий от имени одной или нескольких социальных ролей, но испытывает небольшие трудности | Умеет выполнять различные социальные роли и выступать от имени взятой на себя социальной роли |
| Умение отвечать и задавать вопросы | Испытывают затруднения при ответе на вопросы и в формулировании их | Способны хорошо либо ответить на поставленный вопрос либо сформулировать его | Умеет грамотно отвечать на поставленные вопросы и их формулировать |
| Учебно-познавательная компетенция | |||
| Планирование познавательной деятельности | Не способен самостоятельно спланировать свою учебную познавательную деятельность | Способен самостоятельно спланировать свою познавательную деятельность | Организовывает собственную познавательную деятельность, умеет прогнозировать результаты своей работы |
| Нахождение, переработка, использование информации для решения учебных задач/ситуаций | Испытывает затруднение в нахождении, переработке и использовании информации для решения задания в известной неизменяющейся ситуации | Способен при помощи учителя найти, переработать и использовать информацию для решения заданий в предсказуемых изменяемых условиях
| Способен находить, перерабатывать и использовать информацию для решения учебных заданий в новых незнакомых ситуациях |
| Применение знаний в нестандартной ситуации | Способен выполнить задания воспроизводящего характера с помощью учителя | Способен выполнить задания выходящее за рамки стандартных ситуаций при помощи учителя (самостоятельное выполнение заданий воспроизводящего характера, а творческого при помощи учителя) | Умеет выполнять задания, порождать новые решения, как в стандартных, так и нестандартных ситуациях (выполнение заданий как воспроизводящего, так и творческого характера) |
| Проектная и исследовательская деятельность | Испытывает затруднения при выполнении проектной и исследовательской деятельности, не предполагающей использования инновационных подходов и методов решения | Способен к выполнению проектной и исследовательской деятельности. Нуждается в помощи учителя в организации и проведении исследовательской и проектной деятельности, в поиске подходов и методов решения | Вовлечен в проектную и исследовательскую деятельность предполагающая получение нового знания, требующих различных инновационных подходов и методов решения |
| Способность ставить и задавать вопросы по сути проблемы и отыскивать на них ответ | Не задает вопросы по сути проблемы, не замечает свои ошибки и не умеет их исправлять | Не всегда задает вопросы по сути проблемы, но способен устранить и исправить допущенные ошибки по рекомендации учителя | Задает вопросы по сути проблемы, замечает свои ошибки и умеет их исправлять |
| Анализ, рефлексия, самооценка учебно-познавательной деятельности | Испытывают затруднение в анализе, рефлексии и оценке своей познавательной деятельности | Способны осуществлять указанные действия, но испытывают затруднения в адекватной оценке своей учебно-познавательной деятельности | Способны адекватно себя оценивать и проводить рефлексию своей учебно-познавательной деятельности |
| Умение анализировать, выделять главное, отбрасывать второстепенное, находить причинно-следственные связи, систематизировать, отыскивать доказательства | Испытывают затруднения в осуществлении мыслительных операций: анализ, синтез, сравнение, обобщение | Способны осуществлять указанные действия, но испытывают затруднения в сопоставлении, выделении главного, установления причинно-следственных связей | Умеет анализировать, выделять главное, отбрасывать второстепенное, находить причино-следственные связи, систематизировать, отыскивать доказательства |
Метапредметные результаты оцениваются учителем математики в ходе наблюдения за обучающимися на уроке и во внеурочное время, а также психологом школы в результате тестирования два раза в год.
Содержание учебного курса.
СОДЕРЖАНИЕ КУРСА МАТЕМАТИКИ 5 КЛАССА
Натуральные числа и нуль
Натуральный ряд чисел и его свойства
Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками на числовой прямой. Использование свойств натуральных чисел при решении задач.
Запись и чтение натуральных чисел
Различие между цифрой и числом. Позиционная запись натурального числа, поместное значение цифры, разряды и классы, соотношение между двумя соседними разрядными единицами, чтение и запись натуральных чисел.
Округление натуральных чисел
Необходимость округления. Правило округления натуральных чисел.
Сравнение натуральных чисел, сравнение с числом 0
Понятие о сравнении чисел, сравнение натуральных чисел друг с другом и с нулём, математическая запись сравнений, способы сравнения чисел.
Действия с натуральными числами
Сложение и вычитание, компоненты сложения и вычитания, связь между ними, нахождение суммы и разности, изменение суммы и разности при изменении компонентов сложения и вычитания.
Умножение и деление, компоненты умножения и деления, связь между ними, умножение и сложение в столбик, деление уголком, проверка результата с помощью прикидки и обратного действия.
Переместительный и сочетательный законы сложения и умножения, распределительный закон умножения относительно сложения, обоснование алгоритмов выполнения арифметических действий.
Степень с натуральным показателем
Запись числа в виде суммы разрядных слагаемых, порядок выполнения действий в выражениях, содержащих степень, вычисление значений выражений, содержащих степень.
Числовые выражения
Числовое выражение и его значение, порядок выполнения действий. Числовые выражения. Значение числового выражения.
Порядок действий в числовых выражениях.
Деление с остатком
Деление с остатком на множестве натуральных чисел, свойства деления с остатком. Практические задачи на деление с остатком.
Уравнения.
Уравнения. Корень уравнения. Основные свойства уравнений. Решение текстовых задач с помощью уравнений.
Дроби
Обыкновенные дроби
Доля, часть, дробное число, дробь. Дробное число как результат деления. Правильные и неправильные дроби, смешанная дробь (смешанное число).
Запись натурального числа в виде дроби с заданным знаменателем, преобразование смешанной дроби в неправильную дробь и наоборот.
Сравнение обыкновенных дробей.
Сложение и вычитание обыкновенных дробей. Арифметические действия со смешанными дробями.
Арифметические действия с дробными числами.
Способы рационализации вычислений и их применение при выполнении действий.
Десятичные дроби
Целая и дробная части десятичной дроби. Преобразование десятичных дробей в обыкновенные. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Округление десятичных дробей. Умножение и деление десятичных дробей. Преобразование обыкновенных дробей в десятичные дроби. Конечные и бесконечные десятичные дроби.
Среднее арифметическое чисел
Среднее арифметическое двух чисел. Изображение среднего арифметического двух чисел на числовой прямой. Решение практических задач с применением среднего арифметического. Среднее арифметическое нескольких чисел.
Проценты
Понятие процента. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах. Решение несложных практических задач с процентами.
Решение текстовых задач
Единицы измерений: длины, площади, объёма, массы, времени, скорости. Зависимости между единицами измерения каждой величины. Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость.
Задачи на все арифметические действия
Решение текстовых задач арифметическим способом. Использование таблиц, схем, чертежей, других средств представления данных при решении задачи.
Задачи на движение, работу и покупки
Решение несложных задач на движение в противоположных направлениях, в одном направлении, движение по реке по течению и против течения. Решение задач на совместную работу. Применение дробей при решении задач.
Задачи на части, доли, проценты
Решение задач на нахождение части числа и числа по его части. Решение задач на проценты и доли. Применение пропорций при решении задач.
Логические задачи
Решение несложных логических задач. Решение логических задач с помощью графов, таблиц.
Основные методы решения текстовых задач: арифметический, перебор вариантов.
Элементы статистики, вероятности. Комбинаторные задачи
• Представление данных в виде таблиц, графиков.
• Среднее арифметическое. Среднее значение величины.
• Решение комбинаторных задач.
Наглядная геометрия
Фигуры в окружающем мире. Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Четырехугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Правильные многоугольники. Изображение основных геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Длина отрезка, ломаной. Единицы измерения длины. Построение отрезка заданной длины. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира.
Периметр многоугольника. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближенное измерение площади фигур на клетчатой бумаге. Равновеликие фигуры.
Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры разверток многогранников, цилиндра и конуса.
Понятие объема; единицы объема. Объем прямоугольного параллелепипеда, куба.
Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.
Решение практических задач с применением простейших свойств фигур.
История математикиПоявление цифр, букв, иероглифов в процессе счёта и распределения продуктов на Древнем Ближнем Востоке. Связь с Неолитической революцией.
Рождение шестидесятеричной системы счисления. Появление десятичной записи чисел.
Рождение и развитие арифметики натуральных чисел.
Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Л. Магницкий.
Римская система счисления. Позиционные системы счисления. Обозначение цифр в Древней Руси. Старинные меры длины. Введение метра как единицы длины. Метрическая система мер в России, в Европе. История формирования математических символов. Дроби в Вавилоне, Египте, Риме, на Руси.
РАБОТА С ОДАРЕННЫМИ ДЕТЬМИ.
На уроках проводится работа с одаренными детьми (дифференциация и индивидуализация в обучении):
- разноуровневые задания (обучающие и контролирующие);
- обучение самостоятельной работе (работа самостоятельно с учебником, с дополнительной литературой);
- развивающие задачи, в том числе олимпиадные задачи;
- творческие задания (составить задачу, выражение, кроссворд, ребус, анаграмму и т. д.).
Математика. 5 класс
6 часов в неделю, всего 210 часов
| Номер параграфа | Содержание учебного материала | Характеристика основных видов деятельности ученика (на уровне учебных действий) | |||
|
|
|
| |||
| Глава 1 Натуральные числа | 23ч. | 2 | |||
| 1 | Ряд натуральных чисел | 2 | Описывать свойства натурального ряда. Читать и записывать натуральные числа, сравнивать и упорядочивать их. Распознавать на чертежах, рисунках, в окружающем мире отрезок, прямую, луч, плоскость. Приводить примеры моделей этих фигур. Измерять длины отрезков. Строить отрезки заданной длины. Решать задачи на нахождение длин отрезков. Выражать одни единицы длин через другие. Приводить примеры приборов со шкалами. Строить на координатном луче точку с заданной координатой, определять координату точки. Сравнивать натуральные числа | ||
| 2 | Цифры. Десятичная запись натуральных чисел | 3 | |||
| 3 | Отрезок. Длина отрезка | 5 | |||
| 4 | Плоскость. Прямая. Луч | 4 | |||
| 5 | Шкала. Координатный луч | 3 | |||
| 6 | Сравнение натуральных чисел | 4 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 1 | 1 | |||
| Глава 2 Сложение и вычитание натуральных чисел | 38ч. | 5 | |||
| 7 | Сложение натуральных чисел. Свойства сложения | 5 | Формулировать свойства сложения и вычитания натуральных чисел, записывать эти свойства в виде формул. Приводить примеры числовых и буквенных выражений, формул. Составлять числовые и буквенные выражения по условию задачи. Решать уравнения на основании зависимостей между компонентами действий сложения и вычитания. Решать текстовые задачи с помощью составления уравнений. Распознавать на чертежах и рисунках углы, многоугольники, в частности треугольники, прямоугольники. Распознавать в окружающем мире модели этих фигур. С помощью транспортира измерять градусные меры углов, строить углы заданной градусной меры, строить биссектрису данного угла. Классифицировать углы. Классифицировать треугольники по количеству равных сторон и по видам их углов. Описывать свойства прямоугольника. Находить с помощью формул периметры прямоугольника и квадрата. Решать задачи на нахождение периметров прямоугольника и квадрата, градусной меры углов. Строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи. Распознавать фигуры, имеющие ось симметрии | ||
| 8 | Вычитание натуральных чисел | 6 | |||
| 9 | Числовые и буквенные выражения. Формулы | 3 | |||
|
| Контрольная работа № 2 | 1 | |||
| 10 | Уравнение | 4 | |||
| 11 | Угол. Обозначение углов | 2 | |||
| 12 | Виды углов. Измерение углов | 5 | |||
| 13 | Многоугольники. Равные фигуры | 3 | |||
| 14 | Треугольник и его виды | 4 | |||
| 15 | Прямоугольник. Ось симметрии фигуры | 3 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 3 | 1 | |||
| Глава 3 Умножение и деление натуральных чисел | 45ч. |
| |||
| 16 | Умножение. Переместительное свойство умножения | 5 | Формулировать свойства умножения и деления натуральных чисел, записывать эти свойства в виде формул. Решать уравнения на основании зависимостей между компонентами арифметических действий. Находить остаток при делении натуральных чисел. По заданному основанию и показателю степени находить значение степени числа. Находить площади прямоугольника и квадрата с помощью формул. Выражать одни единицы площади через другие. Распознавать на чертежах и рисунках прямоугольный параллелепипед, пирамиду. Распознавать в окружающем мире модели этих фигур. Изображать развёртки прямоугольного параллелепипеда и пирамиды. Находить объёмы прямоугольного параллелепипеда и куба с помощью формул. Выражать одни единицы объёма через другие. Решать комбинаторные задачи с помощью перебора вариантов | ||
| 17 | Сочетательное и распределительное свойства умножения | 4 | |||
| 18 | Деление | 8 | |||
| 19 | Деление с остатком | 3 | |||
| 20 | Степень числа | 3 | |||
|
| Контрольная работа № 4 | 1 | |||
| 21 | Площадь. Площадь прямоугольника | 5 | |||
| 22 | Прямоугольный параллелепипед. Пирамида | 4 | |||
| 23 | Объём прямоугольного параллелепипеда | 5 | |||
| 24 | Комбинаторные задачи | 4 | |||
|
| Повторение и систематизация учебного материала | 2 | |||
|
| Контрольная работа № 5 | 1 | |||
| Глава 4 Обыкновенные дроби | 20ч. | 6 | |||
| 25 | Понятие обыкновенной дроби | 6 | Распознавать обыкновенную дробь, правильные и неправильные дроби, смешанные числа. Читать и записывать обыкновенные дроби, смешанные числа. Сравнивать обыкновенные дроби с равными знаменателями. Складывать и вычитать обыкновенные дроби с равными знаменателями. Преобразовывать неправильную дробь в смешанное число, смешанное число в неправильную дробь. Уметь записывать результат деления двух натуральных чисел в виде обыкновенной дроби | ||
| 26 | Правильные и неправильные дроби. Сравнение дробей | 3 | |||
| 27 | Сложение и вычитание дробей с одинаковыми знаменателями | 2 | |||
| 28 | Дроби и деление натуральных чисел | 1 | |||
| 29 | Смешанные числа | 6 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 6 | 1 | |||
| Глава 5 Десятичные дроби | 55ч. |
| |||
| 30 | Представление о десятичных дробях | 5 | Распознавать, читать и записывать десятичные дроби. Называть разряды десятичных знаков в записи десятичных дробей. Сравнивать десятичные дроби. Округлять десятичные дроби и натуральные числа. Выполнять прикидку результатов вычислений. Выполнять арифметические действия над десятичными дробями. Находить среднее арифметическое нескольких чисел. Приводить примеры средних значений величины. Разъяснять, что такое один процент. Представлять проценты в виде десятичных дробей и десятичные дроби в виде процентов. Находить процент от числа и число по его процентам | ||
| 31 | Сравнение десятичных дробей | 4 | |||
| 32 | Округление чисел. Прикидки | 3 | |||
| 33 | Сложение и вычитание десятичных дробей | 7 | |||
|
| Контрольная работа № 7 | 1 | |||
| 34 | Умножение десятичных дробей | 18 | |||
| 35 | Деление десятичных дробей | 10 | |||
|
| Контрольная работа № 8 | 1 | |||
| 36 | Среднее арифметическое. Среднее значение величины | 3 | |||
| 37 | Проценты. Нахождение процентов от числа | 5 | |||
| 38 | Нахождение числа по его процентам | 5 |
| ||
|
| Повторение и систематизация учебного материала | 2 | |||
|
| Контрольная работа № 9 | 1 | |||
| Повторение и систематизация учебного материала | 29ч. | 28 | |||
| 39 | Упражнения для повторения курса 5 класса | 28 |
| ||
|
| Контрольная работа № 10 | 1 |
| ||
Математика. 6 класс
6 часов в неделю, всего 210 часов
| Номер параграфа | Содержание учебного материала | Характеристика основных видов деятельности ученика (на уровне учебных действий) | |||
|
|
|
| |||
| Глава 1 Делимость натуральных чисел | 22ч. |
| |||
| 1 | Делители и кратные | 3 | Формулировать определения понятий: делитель, кратное, простое число, составное число, общий делитель, наибольший общий делитель, взаимно простые числа, общее кратное, наименьшее общее кратное и признаки делимости на 2, на 3, на 5, на 9, на 10. Описывать правила нахождения наибольшего общего делителя (НОД), наименьшего общего кратного (НОК) нескольких чисел, разложения натурального числа на простые множители | ||
| 2 | Признаки делимости на 10, на 5, на 2 | 3 | |||
| 3 | Признаки делимости на 9 и на 3 | 4 | |||
| 4 | Простые и составные числа | 2 | |||
| 5 | Наибольший общий делитель | 4 | |||
| 6 | Наименьшее общее кратное | 4 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 1 | 1 | |||
| Глава 2 Обыкновенные дроби | 47ч. |
| |||
| 7 | Основное свойство дроби | 3 | Формулировать определения понятий: несократимая дробь, общий знаменатель двух дробей, взаимно обратные числа. Применять основное свойство дроби для сокращения дробей. Приводить дроби к новому знаменателю. Сравнивать обыкновенные дроби. Выполнять арифметические действия над обыкновенными дробями. Находить дробь от числа и число по заданному значению его дроби. Преобразовывать обыкновенные дроби в десятичные. Находить десятичное приближение обыкновенной дроби | ||
| 8 | Сокращение дробей | 4 | |||
| 9 | Приведение дробей к общему знаменателю. Сравнение дробей | 4 | |||
| 10 | Сложение и вычитание дробей | 5 | |||
|
| Контрольная работа № 2 | 1 | |||
| 11 | Умножение дробей | 6 | |||
| 12 | Нахождение дроби от числа | 4 | |||
|
| Контрольная работа № 3 | 1 | |||
| 13 | Взаимно обратные числа | 1 | |||
| 14 | Деление дробей | 6 | |||
| 15 | Нахождение числа по значению его дроби | 4 | |||
| 16 | Преобразование обыкновенных дробей в десятичные | 2 | |||
| 17 | Бесконечные периодические десятичные дроби | 2 |
| ||
| 18 | Десятичное приближение обыкновенной дроби | 2 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 4 | 1 | |||
| Глава 3 Отношения и пропорции | 35ч. |
| |||
| 19 | Отношения | 3 | Формулировать определения: отношения, пропорции, процентного отношения двух чисел, прямо пропорциональных и обратно пропорциональных величин. Применять основное свойство отношения и основное свойство пропорции. Приводить примеры и описывать свойства величин, находящихся в прямой и обратной пропорциональных зависимостях. Находить процентное отношение двух чисел. Делить число на пропорциональные части. Записывать с помощью букв основные свойства дроби, отношения, пропорции. Анализировать информацию, представленную в виде столбчатых и круговых диаграмм. Представлять информацию в виде столбчатых и круговых диаграмм. Приводить примеры случайных событий. Находить вероятность случайного события в опытах с равновозможными исходами. Распознавать на чертежах и рисунках окружность, круг, цилиндр, конус, сферу, шар и их элементы. Распознавать в окружающем мире модели этих фигур. Строить с помощью циркуля окружность заданного радиуса. Изображать развёртки цилиндра и конуса. Называть приближённое значение числа π. Находить с помощью формул длину окружности, площадь круга | ||
| 20 | Пропорции | 5 | |||
| 21 | Процентное отношение двух чисел | 4 | |||
|
| Контрольная работа № 5 | 1 | |||
| 22 | Прямая и обратная пропорциональные зависимости | 3 | |||
| 23 | Деление числа в данном отношении | 2 | |||
| 24 | Окружность и круг | 3 | |||
| 25 | Длина окружности. Площадь круга | 4 | |||
| 26 | Цилиндр, конус, шар | 1 | |||
| 27 | Диаграммы | 3 | |||
| 28 | Случайные события. Вероятность случайного события | 3 | |||
|
| Повторение и систематизация учебного материала | 2 | |||
|
| Контрольная работа № 6 | 1 | |||
| Глава 4 Рациональные числа и действия над ними | 79ч. |
| |||
| 29 | Положительные и отрицательные числа | 2 | Приводить примеры использования положительных и отрицательных чисел. Формулировать определение координатной прямой. Строить на координатной прямой точку с заданной координатой, определять координату точки. Характеризовать множество целых чисел. Объяснять понятие множества рациональных чисел. Формулировать определение модуля числа. Находить модуль числа. | ||
| 30 | Координатная прямая | 3 | |||
| 31 | Целые числа. Рациональные числа | 2 | |||
| 32 | Модуль числа | 4 | Сравнивать рациональные числа. Выполнять арифметические действия над рациональными числами. Записывать свойства арифметических действий над рациональными числами в виде формул. Называть коэффициент буквенного выражения. Применять свойства при решении уравнений. Решать текстовые задачи с помощью уравнений. Распознавать на чертежах и рисунках перпендикулярные и параллельные прямые, фигуры, имеющие ось симметрии, центр симметрии. Указывать в окружающем мире модели этих фигур. Формулировать определение перпендикулярных прямых и параллельных прямых. Строить с помощью угольника перпендикулярные прямые и параллельные прямые. Объяснять и иллюстрировать понятие координатной плоскости. Строить на координатной плоскости точки с заданными координатами, определять координаты точек на плоскости. Строить отдельные графики зависимостей между величинами по точкам. Анализировать графики зависимостей между величинами (расстояние, время; температура и т. п.) | ||
| 33 | Сравнение чисел | 4 | |||
|
| Контрольная работа № 7 | 1 | |||
| 34 | Сложение рациональных чисел | 4 | |||
| 35 | Свойства сложения рациональных чисел | 3 | |||
| 36 | Вычитание рациональных чисел | 5 | |||
|
| Контрольная работа № 8 | 1 | |||
| 37 | Умножение рациональных чисел | 4 | |||
| 38 | Свойства умножения рациональных чисел | 3 | |||
| 39 | Коэффициент. Распределительное свойство умножения | 6 | |||
| 40 | Деление рациональных чисел | 5 | |||
|
| Контрольная работа № 9 | 1 | |||
| 41 | Решение уравнений | 5 | |||
| 42 | Решение задач с помощью уравнений | 6 |
| ||
|
| Контрольная работа № 10 | 1 | |||
| 43 | Перпендикулярные прямые | 3 | |||
| 44 | Осевая и центральная симметрии | 4 | |||
| 45 | Параллельные прямые | 2 | |||
| 46 | Координатная плоскость | 4 | |||
| 47 | Графики | 3 | |||
|
| Повторение и систематизация учебного материала | 2 | |||
|
| Контрольная работа № 11 | 1 |
| ||
| Повторение и систематизация | 25ч. |
| |||
| 48 | Упражнения для повторения курса 6 класса | 24 |
| ||
|
| Контрольная работа № 12 | 1 |
| ||
Алгебра. 7 класс
4 часа в неделю, всего 140 часов
Номер
параграфа
Содержание учебного
материала
Характеристика основных видов деятельности ученика
(на уровне учебных действий)
Глава 1
Линейное уравнение
с одной переменной
16ч.
1
Введение в алгебру
3
Распознавать числовые выражения и выражения с переменными, линейные уравнения. Приводить примеры выражений с переменными, линейных уравнений. Составлять выражение с переменными по условию задачи. Выполнять преобразования выражений: приводить подобные слагаемые, раскрывать скобки. Находить значение выражения с переменными при заданных значениях переменных. Классифицировать алгебраические выражения. Описывать целые выражения.
Формулировать определение линейного уравнения. Решать линейное уравнение в общем виде. Интерпретировать уравнение как математическую модель реальной ситуации. Описывать схему решения текстовой задачи, применять её для решения задач
2
Линейное уравнение с одной переменной
6
3
Решение задач с помощью уравнений
5
Повторение и систематизация учебного материала
1
Контрольная работа № 1
1
Глава 2
Целые выражения
68ч.
4
Тождественно равные выражения. Тождества
2
Формулировать:
определения: тождественно равных выражений, тождества, степени с натуральным показателем, одночлена, стандартного вида одночлена, коэффициента одночлена, степени одночлена, многочлена, степени многочлена;
свойства: степени с натуральным показателем, знака степени;
правила: доказательства тождеств, умножения одночлена на многочлен, умножения многочленов.
Доказывать свойства степени с натуральным показателем.
Записывать и доказывать формулы: произведения суммы и разности двух выражений, разности квадратов двух выражений, квадрата суммы и квадрата разности двух выражений, квадрата суммы нескольких выражений, куба суммы и куба разности двух выражений, суммы кубов и разности кубов двух выражений, формулы для разложения на множители выражений вида an – bn и an + bn.
Вычислять значение выражений с переменными. Применять свойства степени для преобразования выражений. Выполнять умножение одночленов и возведение одночлена в степень. Приводить одночлен к стандартному виду. Записывать многочлен в стандартном виде, определять степень многочлена. Преобразовывать произведение одночлена и многочлена; суммы, разности, произведения двух многочленов в многочлен. Выполнять разложение многочлена на множители способом вынесения общего множителя за скобки, способом группировки, по формулам сокращённого умножения и с применением нескольких способов. Использовать указанные преобразования в процессе решения уравнений, доказательства утверждений, решения текстовых задач
5
Степень с натуральным показателем
2
6
Свойства степени с натуральным показателем
4
7
Одночлены
3
8
Многочлены
2
9
Сложение и вычитание многочленов
4
Контрольная работа № 2
1
10
Умножение одночлена на многочлен
4
11
Умножение многочлена на многочлен
5
12
Разложение многочленов на множители. Вынесение общего множителя за скобки
4
13
Разложение многочленов на множители. Метод группировки
4
Контрольная работа № 3
1
14
Произведение разности и суммы двух выражений
3
15
Разность квадратов двух выражений
3
16
Квадрат суммы и квадрат разности двух выражений. Квадрат суммы нескольких выражений
5
17
Преобразование многочлена в квадрат суммы или разности двух выражений либо в квадрат суммы нескольких выражений
3
Контрольная работа № 4
1
18
Сумма и разность кубов двух выражений
3
19
Куб суммы и куб разности двух выражений
3
20
Применение различных способов разложения многочлена на множители
7
21
Формулы для разложения на множители выражений вида
an – bn и an + bn
2
Повторение и систематизация учебного материала
1
Контрольная
работа № 5
1
Глава 3
Функции
18ч.
22
Множество и его элементы
2
Приводить примеры множеств, зависимостей между величинами. Различать среди зависимостей функциональные зависимости.
Описывать понятия: множества, пустого множества, зависимой и независимой переменных, функции, аргумента функции; способы задания множества и функции. Формулировать определения: равных множеств, области определения функции, области значений функции, графика функции, линейной функции, прямой пропорциональности.
Вычислять значение функции по заданному значению аргумента. Составлять таблицы значений функции. Строить график функции, заданной таблично. По графику функции, являющейся моделью реального процесса, определять характеристики этого процесса. Строить график линейной функции. Описывать свойства этих функций
23
Связи между величинами. Функция
3
24
Способы задания функции
4
25
График функции
3
26
Линейная функция, её график и свойства
4
Повторение и систематизация учебного материала
1
Контрольная работа № 6
1
Глава 4
Системы линейных уравнений
с двумя переменными
20ч.
27
Уравнения с двумя переменными
2
Приводить примеры: уравнения с двумя переменными; линейного уравнения с двумя переменными; системы двух линейных уравнений с двумя переменными; реальных процессов, для которых уравнение с двумя переменными или система уравнений с двумя переменными являются математическими моделями.
Определять, является ли пара чисел решением данного уравнения с двумя переменными.
Формулировать:
определения: решения уравнения с двумя переменными; что значит решить уравнение с двумя переменными; графика уравнения с двумя переменными; линейного уравнения с двумя переменными; решения системы уравнений с двумя переменными;
свойства уравнений с двумя переменными.
Описывать: свойства графика линейного уравнения в зависимости от значений коэффициентов, графический метод решения системы двух уравнений с двумя переменными, метод подстановки и метод сложения для решения системы двух линейных уравнений с двумя переменными.
Строить график линейного уравнения с двумя переменными. Решать системы двух линейных уравнений с двумя переменными.
Решать текстовые задачи, в которых система двух линейных уравнений с двумя переменными является математической моделью реального процесса, и интерпретировать результат решения системы
28
Линейное уравнение с двумя переменными и его график
3
29
Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными
4
30
Решение систем линейных уравнений методом подстановки
2
31
Решение систем линейных уравнений методом сложения
3
32
Решение задач с помощью систем линейных уравнений
4
Повторение и систематизация учебного материала
1
Контрольная
работа № 7
1
Глава 5
Элементы комбинаторики
и описательной статистики
6ч.
33
Основные правила комбинаторики
2
Описывать, что́ является предметом изучения комбинаторики, этапы статистического исследования, понятия выборки, генеральной совокупности, статистические характеристики совокупности данных: среднее значение, мода, размах, медиана выборки.
Уметь представлять и читать данные в виде таблиц, круговых и столбчатых диаграмм, графиков.
Формулировать комбинаторные правила произведения и суммы, определение статистики.
Решать комбинаторные задачи на применение правил произведения и суммы.
Проводить простейшие статистические исследования
34
Начальные сведения о статистике
2
Повторение и систематизация учебного материала
1
Контрольная работа № 8
1
Повторение и систематизация
учебного материала
12ч.
Повторение и систематизация курса алгебры 7 класса
11
Контрольная работа № 9
1
Алгебра. 8 класс
4 часа в неделю, всего 140 часов
| Номер параграфа | Содержание учебного материала | Характеристика основных видов деятельности ученика (на уровне учебных действий) | |||
|
|
|
| |||
| Глава 1 Множества и операции над ними | 10ч. |
| |||
| 1 | Множество. Подмножества данного множества | 2 | Приводить примеры множеств, элементов множества, названий множеств, счётных и несчётных множеств, применения операций над множествами. Описывать способы задания множеств, понятие мощности множества. Иллюстрировать операции над множествами с помощью диаграмм Эйлера. Формулировать определения: равных множеств, подмножества данного множества, пересечения множеств, объединения множеств, разности множеств, взаимно однозначного соответствия между двумя множествами, равномощных множеств, счётного множества. Находить пересечение, объединение, разность данных множеств. Доказывать формулу включений-исключений для двух и трёх множеств. Применять формулу включений-исключений для решения задач. Устанавливать взаимно однозначное соответствие между двумя равномощными множествами | ||
| 2 | Операции над множествами | 3 | |||
| 3 | Формула включения-исключения. Взаимно однозначное соответствие | 2 | |||
| 4 | Счётные множества | 1 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 1 |
| |||
| Глава 2 Рациональные выражения | 31ч. |
| |||
| 5 | Рациональные дроби | 1 | Распознавать целые рациональные выражения, дробные рациональные выражения, приводить примеры таких выражений. Формулировать: определения: рационального выражения, рациональной дроби, области определения выражения, тождественно равных выражений, тождества, области определения уравнения, равносильных уравнений, уравнения-следствия, постороннего корня, рационального уравнения, степени с нулевым показателем, степени с целым отрицательным показателем, стандартного вида числа, обратной пропорциональности; свойства: основное свойство рациональной дроби, степени с целым показателем, уравнений, функции правила: сложения, вычитания, умножения, деления рациональных дробей, возведение рациональной дроби в степень; условие равенства дроби нулю. Доказывать свойства степени с целым показателем, свойства равносильных уравнений. Описывать графический метод решения уравнений с одной переменной. Применять основное свойство рациональной дроби для сокращения и преобразования рациональных дробей. Приводить рациональные дроби к новому (общему) знаменателю. Находить сумму, разность, произведение и частное рациональных дробей, возводить рациональную дробь в степень. Выполнять тождественные преобразования рациональных выражений. Применять свойства степени с целым показателем для преобразования выражений. Записывать числа в стандартном виде. Решать уравнения с переменной в знаменателе дроби, рациональные уравнения с параметрами. Выполнять построение и чтение графика функции | ||
| 6 | Основное свойство рациональной дроби | 2 | |||
| 7 | Сложение и вычитание рациональных дробей с одинаковыми знаменателями | 2 | |||
| 8 | Сложение и вычитание рациональных дробей с разными знаменателями | 4 | |||
|
| Контрольная работа № 2 | 1 | |||
| 9 | Умножение и деление рациональных дробей. Возведение рациональной дроби в степень | 2 | |||
| 10 | Тождественные преобразования рациональных выражений | 5 | |||
|
| Контрольная работа № 3 | 1 | |||
| 11 | Равносильные уравнения. Уравнение-следствие. Рациональные уравнения | 2 | |||
| 12 | Рациональные уравнения с параметрами | 2 | |||
| 13 | Степень с целым отрицательным показателем | 2 | |||
| 14 | Свойства степени с целым показателем | 3 | |||
| 15 | Функция | 2 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 4 | 1 | |||
| Глава 3 Основы теории делимости | 15ч. |
| |||
| 16 | Делимость нацело и её свойства | 3 | Формулировать: определения: делимости нацело, чисел, сравнимых по данному модулю, наибольшего общего делителя двух чисел, наименьшего общего кратного двух чисел, взаимно простых чисел, простого числа, составного числа; свойства: делимости нацело, чисел, сравнимых по данному модулю, наибольшего общего делителя, наименьшего общего кратного, взаимно простых чисел, простых чисел; основные свойства сравнения; признаки делимости: на 9, 3, 11. Описывать: алгоритм Эвклида Доказывать теоремы: о свойствах деления нацело, о делении с остатком, о свойствах чисел, сравнимых по модулю, о признаках делимости на 9, 3, 11, о свойствах НОД и НОК двух чисел, о бесконечности множества простых чисел. Доказывать основную теорему арифметики, малую теорему Ферма. Решать задачи на делимость | ||
| 17 | Деление с остатком. Сравнения по модулю и их свойства | 4 | |||
| 18 | Наибольший общий делитель и наименьшее общее кратное двух натуральных чисел. Взаимно простые числа | 2 | |||
| 19 | Признаки делимости | 2 | |||
| 20 | Простые и составные числа | 2 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 5 | 1 | |||
| Глава 4 Неравенства | 15ч. |
| |||
| 21 | Числовые неравенства и их свойства | 2 | Распознавать и приводить примеры числовых неравенств, неравенств с переменными, линейных неравенств с одной переменной, двойных неравенств. Формулировать: определения: сравнения двух чисел, решения неравенства с одной переменной, равносильных неравенств, неравенства-следствия, решения системы и совокупности неравенств с одной переменной; свойства числовых неравенств, сложения и умножения числовых неравенств; теоремы о равносильности неравенств с одной переменной, о решении уравнений и неравенств, содержащих знак модуля. Доказывать: свойства числовых неравенств, теоремы о сложении и умножении числовых неравенств, о равносильности неравенств с одной переменной. Решать линейные неравенства. Записывать решения неравенств и их систем в виде числовых промежутков, объединения, пересечения числовых промежутков. Решать систему и совокупность неравенств с одной переменной, неравенства, содержащие знак модуля. Оценивать значение выражения. Изображать на координатной прямой заданные неравенствами числовые промежутки | ||
| 22 | Сложение и умножение числовых неравенств. Оценивание значения выражения | 2 | |||
| 23 | Неравенства с одной переменной. Числовые промежутки | 2 | |||
| 24 | Системы и совокупности линейных неравенств с одной переменной | 4 | |||
| 25 | Уравнения и неравенства, содержащие знак модуля | 3 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 6 | 1 | |||
| Глава 5 Квадратные корни. Действительные числа | 19ч. |
| |||
| 26 | Функция y = x2 и её график | 2 | Описывать: множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел и связи между этими числовыми множествами; связь между бесконечными десятичными дробями и рациональными, иррациональными числами. Распознавать рациональные и иррациональные числа. Приводить примеры рациональных чисел и иррациональных чисел. Записывать с помощью формул свойства действий с действительными числами. Формулировать: определения: квадратного корня из числа, арифметического квадратного корня из числа, множества действительных чисел; свойства: функции y = x2, арифметического квадратного корня, функции Доказывать свойства арифметического квадратного корня. Строить графики функций y = x2 и Применять понятие арифметического квадратного корня для вычисления значений выражений. Упрощать выражения, содержащие арифметические квадратные корни. Решать уравнения. Сравнивать значения выражений. Выполнять преобразование выражений с применением вынесения множителя из-под знака корня, внесения множителя под знак корня. Выполнять освобождение от иррациональности в знаменателе дроби, анализ соотношений между числовыми множествами и их элементами | ||
| 27 | Квадратные корни. Арифметический квадратный корень | 3 | |||
| 28 | Множество действительных чисел | 2 | |||
| 29 | Свойства арифметического квадратного корня | 4 | |||
| 30 | Тождественные преобразования выражений, содержащих арифметические квадратные корни | 4 | |||
| 31 | Функция | 2 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 7 | 1 | |||
| Глава 6 Квадратные уравнения | 37ч. |
| |||
| 32 | Квадратные уравнения. Решение неполных квадратных уравнений | 3 | Распознавать и приводить примеры квадратных уравнений различных видов (полных, неполных, приведённых), квадратных трёхчленов. Описывать в общем виде решение неполных квадратных уравнений. Формулировать: определения: уравнения первой степени, квадратного уравнения; квадратного трёхчлена, дискриминанта квадратного уравнения и квадратного трёхчлена, корня квадратного трёхчлена; биквадратного уравнения; деления нацело многочленов, корня многочлена, целого рационального уравнения; свойства квадратного трёхчлена; теорему Виета и обратную ей теорему, теорему о делении многочленов с остатком, теорему Безу, теорему о целом корне целого рационального уравнения. Записывать и доказывать формулу корней квадратного уравнения. Исследовать количество корней квадратного уравнения в зависимости от знака его дискриминанта. Доказывать теоремы: Виета (прямую и обратную), о разложении квадратного трёхчлена на множители, о свойстве квадратного трёхчлена с отрицательным дискриминантом, теорему Безу и следствия из неё, теорему о целом корне целого рационального уравнения. Описывать на примерах метод замены переменной для решения уравнений. Находить корни квадратных уравнений различных видов. Применять теорему Виета и обратную ей теорему. Выполнять разложение квадратного трёхчлена на множители. Находить корни уравнений, которые сводятся к квадратным. Составлять квадратные уравнения и уравнения, сводящиеся к квадратным, являющиеся математическими моделями реальных ситуаций. Решать уравнения методом замены переменной. Находить целые корни целого рационального уравнения | ||
| 33 | Формула корней квадратного уравнения | 3 | |||
| 34 | Теорема Виета | 4 | |||
|
| Контрольная работа № 8 | 1 | |||
| 35 | Квадратный трёхчлен | 4 | |||
| 36 | Решение уравнений, приводимых к квадратным уравнениям | 4 | |||
| 37 | Решение уравнений методом замены переменной | 6 | |||
| 38 | Рациональные уравнения как математические модели реальных ситуаций | 4 | |||
| 39 | Деление многочленов | 2 | |||
| 40 | Корни многочлена. Теорема Безу | 2 | |||
| 41 | Целое рациональное уравнение | 2 | |||
|
| Повторение и систематизация учебного материала | 1 | |||
|
| Контрольная работа № 9 | 1 | |||
| Повторение и систематизация | 13ч. |
| |||
|
| Повторение и систематизация курса алгебры 8 класса | 12 |
| ||
|
| Контрольная работа № 10 | 1 |
| ||
Алгебра. 9 класс
4 часа в неделю, всего 140 часов
Номер
параграфа
Содержание учебного
материала
Характеристика основных видов деятельности ученика
(на уровне учебных действий)
Глава 1
Квадратичная функция
40ч.
1
Функция
3
Описывать понятия: функции как правила, устанавливающего связь между элементами двух множеств, отображения одного множества на другое как синоним понятия функции, сложной функции.
Описывать способы задания функции, метод интервалов.
Формулировать:
определения: графика функции, нуля функции; промежутков знакопостоянства функции; функции, возрастающей (убывающей) на множестве; чётной и нечётной функции, наибольшего и наименьшего значений функции, квадратичной функции; квадратного неравенства;
теоремы о свойствах: возрастающей и убывающей функции, чётной и нечётной функций;
свойства квадратичной функции; правила построения графиков функций с помощью преобразований вида f (x) → f (x) + b, f (x) → f (x + а), f (x) → kf (x),
f (x) → f (kx), f (x) → f (|x|) и f (x) → | f (x)|.
Доказывать: теоремы о свойствах возрастающей (убывающей) функции, чётной и нечётной функций.
Строить графики функций с помощью преобразований вида f (x) → f (x) + а,
f (x) → f (x + а), f (x) → kf (x), f (x) → f (kx), f (x) → f (|x|) и f (x) → | f (x)|.
Строить график квадратичной функции. По графику квадратичной функции описывать её свойства.
Описывать схематичное расположение параболы относительно оси абсцисс в зависимости от знака старшего коэффициента и дискриминанта соответствующего квадратного трёхчлена.
Решать квадратные неравенства, используя схему расположения параболы относительно оси абсцисс, неравенства методом интервалов.
Исследовать условия расположения нулей квадратичной функции относительно заданных точек
2
Возрастание и убывание функции. Наибольшее и наименьшее значения функции
5
3
Чётные и нечётные функции
2
4
Построение графиков функций y = kf (x), y = f (kx)
3
5
Построение графиков функций y = f (x) + b и y = f (x + a)
3
6
Построение графиков функций y = f (|x|) и y = | f (x)|
3
Контрольная работа № 1
1
7
Квадратичная функция, её график и свойства
5
8
Решение квадратных нерaвенств
4
9
Решение неравенств методом интервалов
6
10
Расположение нулей квадратичной функции относительно данной точки
3
Повторение и систематизация учебного материала
1
Контрольная работа № 2
1
Глава 2
Уравнения с двумя переменными
и их системы
18ч.
11
Уравнение с двумя переменными и его график
4
Описывать графический метод решения системы двух уравнений с двумя переменными, метод подстановки и метод сложения и умножения, метод замены переменных для решения системы двух уравнений с двумя переменными.
Формулировать:
определения: решения уравнения с двумя переменными, графика уравнения с двумя переменными, равносильных систем уравнений с двумя переменными, системы-следствия, однородного многочлена, симметрического многочлена;
правила построения графиков уравнений с помощью преобразований вида
F(x; y) = 0 → F(x + a; y) = 0, F(x; y) = 0 → F(x; y + b) = 0, F(x; y) = 0 → F(–x; y) = 0,
F(x; y) = 0 → F(x; –y) = 0, F(x; y) = 0 → F(kx; y) = 0, F(x; y) = 0 → F(x; ky) = 0,
F(x; y) = 0 → F(|x|; y) = 0, F(x; y) = 0 → F(x; |y|) = 0;
методы: подстановки, сложения, умножения, замены переменных для систем двух уравнений с двумя переменными;
теоремы: о свойствах равносильных систем уравнений, о симметрическом многочлене
12
Графические методы решения систем уравнений с двумя переменными
3
13
Решение систем уравнений с двумя переменными методом подстановки и методами сложения и умножения
4
14
Метод замены переменных и другие способы решения систем уравнений с двумя переменными
5
Повторение и систематизация учебного материала
1
Контрольная работа № 3
1
Глава 3
Неравенства с двумя переменными
и их системы.
Доказательство неравенств
17ч.
15
Неравенства с двумя переменными
3
Описывать понятия: неравенства с двумя переменными, системы неравенств с двумя переменными, графические методы решения систем двух неравенств с двумя переменными.
Описывать: основные методы доказательства неравенств.
Формулировать:
определения: решения неравенства с двумя переменными, графика неравенства с двумя переменными, линейного неравенства с двумя переменными, равносильных систем уравнений с двумя переменными.
Доказывать: неравенства между средними величинами, неравенство Коши — Буняковского.
Изображать на координатной плоскости множества точек, задаваемые неравенствами с двумя переменными и их системами.
Применять основные методы доказательства неравенств
16
Системы неравенств с двумя переменными
3
17
Основные методы доказательства неравенств
5
18
Неравенства между средними величинами. Неравенство Коши — Буняковского
4
Повторение и систематизация учебного материала
1
Контрольная работа № 4
1
Глава 4
Элементы прикладной математики
10ч.
19
Математическое моделирование
3
Приводить примеры:
математических моделей реальных ситуаций; прикладных задач; приближённых величин.
Формулировать:
определения: абсолютной погрешности, относительной погрешности.
Описывать этапы решения прикладной задачи.
Пояснять и записывать формулу сложных процентов. Проводить процентные расчёты с использованием сложных процентов.
Решать текстовые задачи, в которых система двух уравнений с двумя переменными является математической моделью реального процесса, и интерпретировать результат решения системы.
Находить точность приближения по таблице приближённых значений величины. Использовать различные формы записи приближённого значения величины. Оценивать приближённое значение величины
20
Процентные расчёты
3
21
Приближённые вычисления
2
Повторение и систематизация учебного материала
1
Контрольная работа № 5
1
Глава 5
Элементы комбинаторики
и теории вероятностей
19ч.
22
Метод математической индукции
2
Приводить примеры: индуктивных рассуждений, использования комбинаторных правил суммы и произведения; случайных событий, включая достоверные и невозможные события; опытов с равновероятными исходами; использования вероятностных свойств окружающих явлений.
Описывать метод математической индукции, различные схемы доказательства методом математической индукции.
Формулировать:
определения: упорядоченного множества, перестановки, размещения, сочетания, достоверного события, невозможного события; классическое определение вероятности;
правила: комбинаторное правило суммы, комбинаторное правило произведения.
Доказывать формулы: для нахождения количества перестановок, размещений, сочетаний, выражающие свойства сочетаний.
Проводить опыты со случайными исходами.
Пояснять и записывать формулу нахождения частоты случайного события. Описывать статистическую оценку вероятности случайного события. Находить вероятность случайного события в опытах с равновероятными исходами
23
Основные правила комбинаторики. Перестановки
3
24
Размещения
2
25
Сочетания
4
26
Частота и вероятность случайного события
2
27
Классическое определение вероятности
2
28
Вычисление вероятностей с помощью правил комбинаторики
3
Контрольная работа № 6
1
Глава 6
Числовые последовательности
19ч.
29
Числовые последовательности
2
Приводить примеры: последовательностей; числовых последовательностей, в частности арифметической и геометрической прогрессий; числовых последовательностей, имеющих предел; использования последовательностей в реальной жизни; задач, в которых рассматриваются суммы с бесконечным числом слагаемых.
Описывать понятия: последовательности; члена последовательности; конечной последовательности; бесконечной последовательности; последовательности, имеющей предел; способы задания последовательности; в чём состоит задача суммирования.
Вычислять члены последовательности, заданной формулой n-го члена или рекуррентно.
Формулировать:
определения: стационарной последовательности, арифметической прогрессии, геометрической прогрессии;
свойства членов геометрической и арифметической прогрессий.
Задавать арифметическую и геометрическую прогрессии рекуррентно.
Записывать и доказывать: формулы общего члена арифметической и геометрической прогрессий, формулы суммы n первых членов арифметической и геометрической прогрессий; формулы, выражающие свойства членов арифметической и геометрической прогрессий.
Вычислять сумму бесконечной геометрической прогрессии, у которой | q | 1. Представлять бесконечные периодические дроби в виде обыкновенных.
Решать несложные задачи на суммирование
30
Арифметическая прогрессия
3
31
Сумма n первых членов арифметической прогрессии
3
32
Геометрическая прогрессия
3
33
Сумма n первых членов геометрической прогрессии
2
34
Представление о пределе последовательности. Сумма бесконечной геометрической прогрессии, у которой | q | 1
2
35
Суммирование
2
Повторение и систематизация учебного материала
1
Контрольная работа № 7
1
Повторение и систематизация
учебного материала
17ч.
Повторение и систематизация курса алгебры 9 класса
16
Контрольная
работа № 8
1
Геометрия. 7 класс
(2 часа в неделю, всего 70 часов)
Номер
параграфа
Содержание учебного
материала
Количество часов
Характеристика основных видов деятельности ученика
(на уровне учебных действий)
Глава 1
Простейшие
геометрические фигуры
и их свойства
15
1
Точки и прямые
2
Приводить примеры геометрических фигур.
Описывать точку, прямую, отрезок, луч, угол.
Формулировать:
определения: равных отрезков, середины отрезка, расстояния между двумя точками, дополнительных лучей, развёрнутого угла, равных углов, биссектрисы угла, смежных и вертикальных углов, пересекающихся прямых, перпендикулярных прямых, перпендикуляра, наклонной, расстояния от точки до прямой;
свойства: расположения точек на прямой, измерения отрезков и углов, смежных и вертикальных углов, перпендикулярных прямых; основное свойство прямой.
Классифицировать углы.
Доказывать: теоремы о пересекающихся прямых, о свойствах смежных и вертикальных углов, о единственности прямой, перпендикулярной данной (случай, когда точка лежит на данной прямой).
Находить длину отрезка, градусную меру угла, используя свойства их измерений.
Изображать с помощью чертёжных инструментов геометрические фигуры: отрезок, луч, угол, смежные и вертикальные углы, перпендикулярные прямые, отрезки и лучи.
Пояснять, что такое аксиома, определение.
Решать задачи на вычисление и доказательство, проводя необходимые доказательные рассуждения
2
Отрезок и его длина
3
3
Луч. Угол. Измерение углов
3
4
Смежные и вертикальные углы
3
5
Перпендикулярные прямые
1
6
Аксиомы
1
Повторение и систематизация учебного материала
1
Контрольная работа № 1
1
Глава 2
Треугольники
18
7
Равные треугольники. Высота, медиана, биссектриса треугольника
2
Описывать смысл понятия «равные фигуры». Приводить примеры равных фигур.
Изображать и находить на рисунках равносторонние, равнобедренные, прямоугольные, остроугольные, тупоугольные треугольники и их элементы.
Классифицировать треугольники по сторонам и углам.
Формулировать:
определения: остроугольного, тупоугольного, прямоугольного, равнобедренного, равностороннего, разностороннего треугольников; биссектрисы, высоты, медианы треугольника; равных треугольников; серединного перпендикуляра отрезка; периметра треугольника;
свойства: равнобедренного треугольника, серединного перпендикуляра отрезка, основного свойства равенства треугольников;
признаки: равенства треугольников, равнобедренного треугольника.
Доказывать теоремы: о единственности прямой, перпендикулярной данной (случай, когда точка лежит вне данной прямой); три признака равенства треугольников; признаки равнобедренного треугольника; теоремы о свойствах серединного перпендикуляра, равнобедренного и равностороннего треугольников.
Разъяснять, что такое теорема, описывать структуру теоремы. Объяснять, какую теорему называют обратной данной, в чём заключается метод доказательства от противного. Приводить примеры использования этого метода.
Решать задачи на вычисление и доказательство
8
Первый и второй признаки равенства треугольников
5
9
Равнобедренный треугольник и его свойства
4
10
Признаки равнобедренного треугольника
2
11
Третий признак равенства треугольников
2
12
Теоремы
1
Повторение и систематизация учебного материала
1
Контрольная работа № 2
1
Глава 3
Параллельные прямые. Сумма углов треугольника
16
13
Параллельные прямые
1
Распознавать на чертежах параллельные прямые.
Изображать с помощью линейки и угольника параллельные прямые.
Описывать углы, образованные при пересечении двух прямых секущей.
Формулировать:
определения: параллельных прямых, расстояния между параллельными прямыми, внешнего угла треугольника, гипотенузы и катета;
свойства: параллельных прямых; углов, образованных при пересечении параллельных прямых секущей; суммы улов треугольника; внешнего угла треугольника; соотношений между сторонами и углами треугольника; прямоугольного треугольника; основное свойство параллельных прямых;
признаки: параллельности прямых, равенства прямоугольных треугольников.
Доказывать: теоремы о свойствах параллельных прямых, о сумме углов треугольника, о внешнем угле треугольника, неравенство треугольника, теоремы о сравнении сторон и углов треугольника, теоремы о свойствах прямоугольного треугольника, признаки параллельных прямых, равенства прямоугольных треугольников.
Решать задачи на вычисление и доказательство
14
Признаки параллельности прямых
2
15
Свойства параллельных прямых
3
16
Сумма углов треугольника
4
17
Прямоугольный треугольник
2
18
Свойства прямоугольного треугольника
2
Контрольная работа № 3
1
Глава 4
Окружность и круг.
Геометрические построения
16
19
Геометрическое место точек. Окружность и круг
2
Пояснять, что такое задача на построение; геометрическое место точек (ГМТ). Приводить примеры ГМТ.
Изображать на рисунках окружность и её элементы; касательную к окружности; окружность, вписанную в треугольник, и окружность, описанную около него. Описывать взаимное расположение окружности и прямой.
Формулировать:
определения: окружности, круга, их элементов; касательной к окружности; окружности, описанной около треугольника, и окружности, вписанной в треугольник;
свойства: серединного перпендикуляра как ГМТ; биссектрисы угла как ГМТ; касательной к окружности; диаметра и хорды; точки пересечения серединных перпендикуляров сторон треугольника; точки пересечения биссектрис углов треугольника;
признаки касательной.
Доказывать: теоремы о серединном перпендикуляре и биссектрисе угла как ГМТ;
о свойствах касательной; об окружности, вписанной в треугольник, описанной около треугольника; признаки касательной.
Решать основные задачи на построение: построение угла, равного данному; построение серединного перпендикуляра данного отрезка; построение прямой, проходящей через данную точку и перпендикулярной данной прямой; построение биссектрисы данного угла; построение треугольника по двум сторонам и углу между ними; по стороне и двум прилежащим к ней углам.
Решать задачи на построение методом ГМТ.
Строить треугольник по трём сторонам.
Решать задачи на вычисление, доказательство и построение
20
Некоторые свойства окружности. Касательная к окружности
3
21
Описанная и вписанная окружности треугольника
3
22
Задачи на построение
3
23
Метод геометрических мест точек в задачах на построение
3
Повторение и систематизация учебного материала
1
Контрольная работа № 4
1
Обобщение
и систематизация
знаний учащихся
5
Упражнения для повторения курса 7 класса
4
Контрольная работа № 5
1
Геометрия. 8 класс
(2 часа в неделю, всего 70 часов)
Номер
параграфа
Содержание учебного
материала
Количество часов
Характеристика основных видов деятельности ученика
(на уровне учебных действий)
Глава 1
Четырёхугольники
22
1
Четырёхугольник и его элементы
2
Пояснять, что такое четырёхугольник. Описывать элементы четырёхугольника.
Распознавать выпуклые и невыпуклые четырёхугольники.
Изображать и находить на рисунках четырёхугольники разных видов и их элементы.
Формулировать:
определения: параллелограмма, высоты параллелограмма; прямоугольника, ромба, квадрата; средней линии треугольника; трапеции, высоты трапеции, средней линии трапеции; центрального угла окружности, вписанного угла окружности; вписанного и описанного четырёхугольника;
свойства: параллелограмма, прямоугольника, ромба, квадрата, средних линий треугольника и трапеции, вписанного угла, вписанного и описанного четырёхугольника;
признаки: параллелограмма, прямоугольника, ромба, вписанного и описанного четырёхугольника.
Доказывать: теоремы о сумме углов четырёхугольника, о градусной мере вписанного угла, о свойствах и признаках параллелограмма, прямоугольника, ромба, вписанного и описанного четырёхугольника.
Применять изученные определения, свойства и признаки к решению задач
2
Параллелограмм. Свойства параллелограмма
2
3
Признаки параллелограмма
2
4
Прямоугольник
2
5
Ромб
2
6
Квадрат
1
Контрольная работа № 1
1
7
Средняя линия треугольника
1
8
Трапеция
4
9
Центральные и вписанные углы
2
10
Вписанные и описанные четырёхугольники
2
Контрольная работа № 2
1
Глава 2
Подобие треугольников
16
11
Теорема Фалеса. Теорема о пропорциональных отрезках
6
Формулировать:
определение подобных треугольников;
свойства: медиан треугольника, биссектрисы треугольника, пересекающихся хорд, касательной и секущей;
признаки подобия треугольников.
Доказывать:
теоремы: Фалеса, о пропорциональных отрезках, о свойствах медиан треугольника, биссектрисы треугольника;
свойства: пересекающихся хорд, касательной и секущей;
признаки подобия треугольников.
Применять изученные определения, свойства и признаки к решению задач
12
Подобные треугольники
1
13
Первый признак подобия треугольников
5
14
Второй и третий признаки подобия треугольников
3
Контрольная работа № 3
1
Глава 3
Решение прямоугольных
треугольников
14
15
Метрические соотношения в прямоугольном треугольнике
1
Формулировать:
определения: синуса, косинуса, тангенса, котангенса острого угла прямоугольного треугольника;
свойства: выражающие метрические соотношения в прямоугольном треугольнике и соотношения между сторонами и значениями тригонометрических функций в прямоугольном треугольнике.
Записывать тригонометрические формулы, выражающие связь между тригонометрическими функциями одного и того же острого угла.
Решать прямоугольные треугольники.
Доказывать:
теорему о метрических соотношениях в прямоугольном треугольнике, теорему Пифагора;
формулы, связывающие синус, косинус, тангенс, котангенс одного и того же острого угла.
Выводить основное тригонометрическое тождество и значения синуса, косинуса, тангенса и котангенса для углов 30°, 45°, 60°.
Применять изученные определения, теоремы и формулы к решению задач
16
Теорема Пифагора
5
Контрольная работа № 4
1
17
Тригонометрические функции острого угла прямоугольного треугольника
3
18
Решение прямоугольных треугольников
3
Контрольная работа № 5
1
Глава 4
Многоугольники.
Площадь многоугольника
10
19
Многоугольники
1
Пояснять, что такое площадь многоугольника.
Описывать многоугольник, его элементы; выпуклые и невыпуклые многоугольники.
Изображать и находить на рисунках многоугольник и его элементы; многоугольник, вписанный в окружность, и многоугольник, описанный около окружности.
Формулировать:
определения: вписанного и описанного многоугольника, площади многоугольника, равновеликих многоугольников;
основные свойства площади многоугольника.
Доказывать: теоремы о сумме углов выпуклого n-угольника, площади прямоугольника, площади треугольника, площади трапеции.
Применять изученные определения, теоремы и формулы к решению задач
20
Понятие площади
многоугольника.
Площадь прямоугольника
1
21
Площадь параллелограмма
2
22
Площадь треугольника
2
23
Площадь трапеции
3
Контрольная работа № 6
1
Повторение
и систематизация
учебного материала
8
Упражнения для повторения курса 8 класса
7
Контрольная работа № 7
1
Геометрия. 9 класс
(2 часа в неделю, всего 70 часов)
Номер
параграфа
Содержание учебного
материала
Количество часов
Характеристика основных видов деятельности ученика
(на уровне учебных действий)
Глава 1
Решение треугольников
16
1
Синус, косинус, тангенс и котангенс угла от 0° до 180°
2
Формулировать:
определения: синуса, косинуса, тангенса, котангенса угла от 0° до 180°;
свойство связи длин диагоналей и сторон параллелограмма.
Формулировать и разъяснять основное тригонометрическое тождество. Вычислять значение тригонометрической функции угла по значению одной из его заданных функций.
Формулировать и доказывать теоремы: синусов, косинусов, следствия из теоремы косинусов и синусов, о площади описанного многоугольника.
Записывать и доказывать формулы для нахождения площади треугольника, радиусов вписанной и описанной окружностей треугольника.
Применять изученные определения, теоремы и формулы к решению задач
2
Теорема косинусов
3
3
Теорема синусов
3
4
Решение треугольников
3
5
Формулы для нахождения площади треугольника
4
Контрольная работа № 1
1
Глава 2
Правильные многоугольники
8
6
Правильные многоугольники и их свойства
4
Пояснять, что такое центр и центральный угол правильного многоугольника, сектор и сегмент круга.
Формулировать:
определение правильного многоугольника;
свойства правильного многоугольника.
Доказывать свойства правильных многоугольников.
Записывать и разъяснять формулы длины окружности, площади круга.
Записывать и доказывать формулы длины дуги, площади сектора, формулы для нахождения радиусов вписанной и описанной окружностей правильного многоугольника.
Строить с помощью циркуля и линейки правильные треугольник, четырёхугольник, шестиугольник.
Применять изученные определения, теоремы и формулы к решению задач
7
Длина окружности. Площадь круга
3
Контрольная работа № 2
1
Глава 3
Декартовы
координаты на плоскости
11
8
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
3
Описывать прямоугольную систему координат.
Формулировать: определение уравнения фигуры, необходимое и достаточное условия параллельности двух прямых.
Записывать и доказывать формулы расстояния между двумя точками, координат середины отрезка.
Выводить уравнение окружности, общее уравнение прямой, уравнение прямой с угловым коэффициентом.
Доказывать необходимое и достаточное условие параллельности двух прямых.
Применять изученные определения, теоремы и формулы к решению задач
9
Уравнение фигуры. Уравнение окружности
3
10
Уравнение прямой
2
11
Угловой коэффициент прямой
2
Контрольная работа № 3
1
Глава 4
Векторы
12
12
Понятие вектора
2
Описывать понятия векторных и скалярных величин. Иллюстрировать понятие вектора.
Формулировать:
определения: модуля вектора, коллинеарных векторов, равных векторов, координат вектора, суммы векторов, разности векторов, противоположных векторов, умножения вектора на число, скалярного произведения векторов;
свойства: равных векторов, координат равных векторов, сложения векторов, координат вектора суммы и вектора разности двух векторов, коллинеарных векторов, умножения вектора на число, скалярного произведения двух векторов, перпендикулярных векторов.
Доказывать теоремы: о нахождении координат вектора, о координатах суммы и разности векторов, об условии коллинеарности двух векторов, о нахождении скалярного произведения двух векторов, об условии перпендикулярности.
Находить косинус угла между двумя векторами.
Применять изученные определения, теоремы и формулы к решению задач
13
Координаты вектора
1
14
Сложение и вычитание векторов
2
15
Умножение вектора на число
3
16
Скалярное произведение векторов
3
Контрольная работа № 4
1
Глава 5
Геометрические
преобразования
13
17
Движение (перемещение) фигуры. Параллельный перенос
4
Приводить примеры преобразования фигур.
Описывать преобразования фигур: параллельный перенос, осевая симметрия, центральная симметрия, поворот, гомотетия, подобие.
Формулировать:
определения: движения; равных фигур; точек, симметричных относительно прямой; точек, симметричных относительно точки; фигуры, имеющей ось симметрии; фигуры, имеющей центр симметрии; подобных фигур;
свойства: движения, параллельного переноса, осевой симметрии, центральной симметрии, поворота, гомотетии.
Доказывать теоремы: о свойствах параллельного переноса, осевой симметрии, центральной симметрии, поворота, гомотетии, об отношении площадей подобных треугольников.
Применять изученные определения, теоремы и формулы к решению задач
18
Осевая и центральная симметрии. Поворот
4
19
Гомотетия. Подобие фигур
4
Контрольная работа № 5
1
Повторение
и систематизация
учебного материала
10
Упражнения для повторения курса 9 класса
9
Контрольная работа № 6
1
Описание учебно-методического и
материально-технического обеспечения учебного процесса
Учебно-методические пособия:
Авторская программа А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко (Математика: программы : 5–9 классы А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко /. — М. : Вентана-Граф, 2013. — 112 с.
Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2014 г.
Математика: 5 класс: дидактические материалы: сборник задач и контрольных работ / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2014.
Математика: 5 класс: рабочая тетрадь №1, №2 / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
Математика: 5 класс: методическое пособие / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
ПЕЧАТНЫЕ ПОСОБИЯ
1. Таблицы по математике для 5 класса.
2. Портреты выдающихся деятелей математики.
ТЕХНИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ
1. Компьютер.
2. Мультимедиа проектор.
3. Экран навесной.
УЧЕБНО-ПРАКТИЧЕСКОЕ И УЧЕБНО-ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ
1. Доска с координатной сеткой.
2. Наборы «Части целого на круге», «Простые дроби».
3. Наборы геометрических тел (демонстрационный).
4. Комплект чертёжных инструментов (классных и личных): линейка, транспортир, угольник (30°, 60°), угольник (45°, 45°), циркуль
ПРИМЕНЕНИЕ ИКТ НА УРОКАХ:
Предусмотрено данной программой применение на уроках ИКТ, в форме наглядных презентаций для устного счета, при изучении материала, для контроля знаний, что обусловлено:
улучшением наглядности изучаемого материала,
увеличением количества предлагаемой информации,
уменьшением времени подачи материала
Интернет-ресурсы:
http://metodsovet.moy.su/,
http://zavuch.info/,
http://nsportal.ru
http://matemproekt56.blogspot.ru/
http://school-collection.edu.ru/
http://infourok.ru/
Подтверждение авторства
Пожалуйста, введите ваш Email.
Если вы хотите увидеть все свои работы, то вам необходимо войти или зарегистрироваться
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
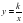 ;
;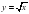 .
.















