Контрольная работа №1
Четырехугольники
Вариант 1
А1. Периметр параллелограмма ABCD равен 80 см.  А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма
А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма
А2. Докажите, что у равнобедренной трапеции углы при основании равны.
А3. Постройте ромб по двум диагоналям. Сколько осей симметрии у ромба?
________________________________________________
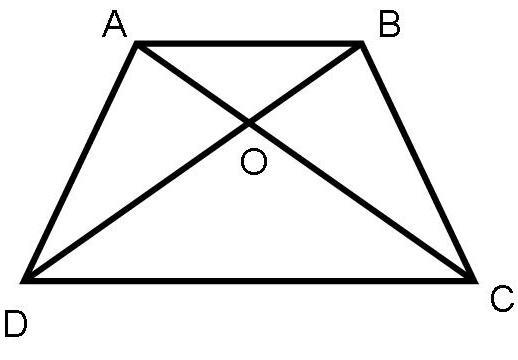
В1. Точки Р, К, L, M – середины сторон ромба АВСD. Докажите, что четырехугольник РКLM – прямоугольник.
________________________________________________________________
Контрольная работа №1
Четырехугольники
Вариант 2
А1. Диагональ квадрата равна 4 см. Сторона его равна диагонали другого квадрата. Найдите сторону последнего.
А2. Докажите, что середины сторон прямоугольника являются вершинами ромба.
А3. Постройте квадрат по диагонали. Сколько осей симметрии имеет квадрат?
________________________________________________
В1. В трапеции АВСD меньшее основание ВС равно 4 см. Через вершину В проведена прямая, параллельная стороне СD. Периметр образовавшегося треугольника равен 12 см. Найдите периметр трапеции.
Контрольная работа №2
Площади фигур
Вариант 1
А1. В прямоугольнике ABCD АВ = 24 см, АС = 25 см. Найдите площадь прямоугольника.
А2. Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см, а острый угол равен 60о.
А3. Найдите площадь ромба, если его диагонали равны 14 и 6 см.
А4. Найдите площадь равнобедренной трапеции, у которой высота равна 16 см, а диагонали взаимно перпендикулярны.
____________________________________________________
В1. Середины оснований трапеции соединены отрезком.
Докажите, что полученные две трапеции равновелики.
________________________________________________________________
Контрольная работа №2
Площади фигур
Вариант 2
А1. В ромбе ABCD АВ = 10 см, меньшая диагональ АС = 12 см. Найдите площадь ромба.
А2. Найдите площадь равнобедренного треугольника, если его боковая сторона равна 6 см, а угол при вершине равен 60о.
А3. Найдите площадь прямоугольника, если его диагональ равна 13 см, а одна из сторон 5 см.
А4. Найдите площадь равнобедренной трапеции, у которой высота равна 16 см, а диагонали взаимно перпендикулярны.
____________________________________________________
В1. Докажите, что медиана треугольника разбивает его на два треугольника одинаковой площади.
Контрольная работа №3
Признаки подобия треугольников
Вариант 1
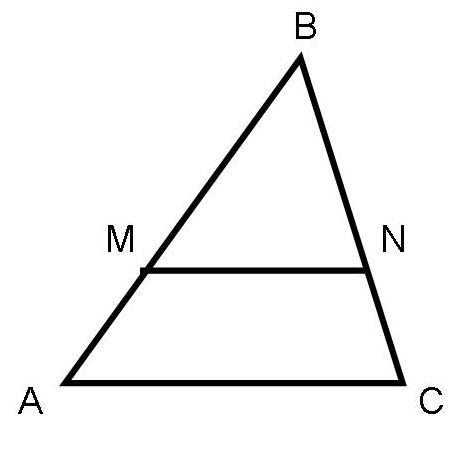
А1. На рисунке АВ || CD.
а) Докажите, что АО : ОС = ВО : OD.
б) Найдите АВ, если OD = 15 см, ОВ = 9 см,
CD = 25 см.
А2. Найдите отношение площадей треугольников ABC и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, КМ = 10 см, MN = 15 см, NK = 20 см.
__________________________________________
В1. Докажите, что в подобных треугольниках отношение двух сходственных сторон равно отношению двух сходственных высот.
____________________________________________________________________
Контрольная работа №3
Признаки подобия треугольников
Вариант 2
А1. На рисунке MN || АС.
а) Докажите, что 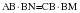 .
.
б) Найдите MN, если AM = 6 см, ВМ = 8 см,
АС = 21 см.
А2. Даны стороны треугольников PКМ и ABC:
PК = 16 см, КМ = 20 см, РМ = 28 см и АВ = 12 см,
ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.
______________________________________
В1. Докажите, что в подобных треугольниках отношение двух сходственных сторон равно отношению двух сходственных биссектрис.
Контрольная работа №4
Подобные треугольники
Вариант 1
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АО=12 см, ОВ=3 см, СО=8 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=9 см, ВС=12 см, АС=15 см и АК : КВ=2:1.
А3. В треугольнике АВС угол С=900. АС=15см, ВС=8 см. Найдите 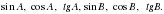
__________________________________________
В1. Между пунктами А и В находится болото. Чтобы найти расстояние между А и В, отметили вне болота произвольную точку С, измерили расстояние АС = 600 м и ВС = 400 м, а также 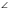 АСВ = 62°.
АСВ = 62°.
Начертите план в масштабе 1 : 10 000 и найдите по нему расстояние между пунктами А и В.
Контрольная работа №4
Подобные треугольники
Вариант 2
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АС=15 см, ВМ=3 см, СО=10 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=16 см, ВС=8 см, АС=15 см и АК =4 см.
А3. В треугольнике АВС угол С=900. АС=4 см, АВ=5 см. Найдите 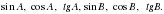
______________________________________
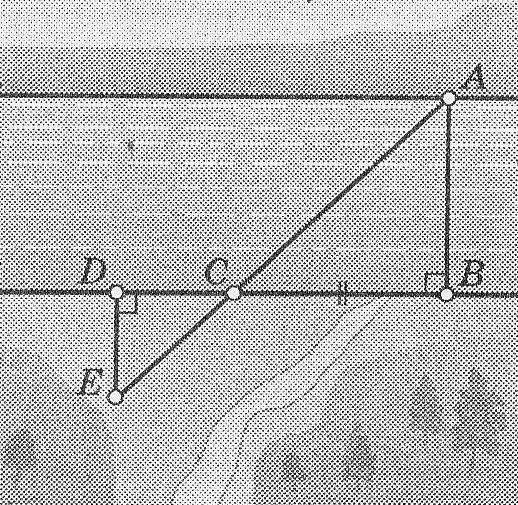
В1. На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Обоснуйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки
(масштаб рисунка 1 : 1000).
Контрольная работа №5
Окружность
Вариант 1
А1. Из точки данной окружности проведены диаметр и хорда, равная радиусу. Найдите угол между ними.
А2. Хорда АВ стягивает дугу, равную 125о, а хорда АС – дугу в 52о. Найдите угол ВАС
А3. Постройте окружность, описанную около тупоугольного треугольника.
_____________________________________________
В1. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Контрольная работа №5
Окружность
Вариант 2
А1. Через точку данной окружности проведены касательная и хорда, равная радиусу. Найдите угол между ними.
А2. Хорда АВ стягивает дугу, равную 75о, а хорда АС – дугу в 112о. Найдите угол ВАС
А3. Постройте окружность, вписанную в данный треугольник.
_____________________________________________
В1. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Контрольная работа №6
Итоговая контрольная работа за курс геометрии 8 класса
Вариант 1
А1. В прямоугольном треугольнике найдите гипотенузу с, если его катеты равны: а=5 см, b=12 см.
А2. В треугольнике АВС 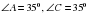 . Найдите
. Найдите 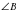 .
.
А3. В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите: а)высоту треугольника, проведенную к основанию треугольника; б) площадь треугольника.
А4. Постройте равнобедренный треугольник по боковой стороне и углу при основании.
__________________________________________________
В1. Около остроугольного треугольника АВС описана окружность с центром О. Расстояние от точки О до прямой АВ равно 6 см, 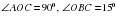 .
.
Найдите: а) угол АВО; б) радиус окружности.
__________________________________________________________________
Контрольная работа №6
Итоговая контрольная работа за курс геометрии 8 класса
Вариант 2
А1. В прямоугольном треугольнике гипотенуза с=25 см, один из его катетов: а=24 см. Найдите другой катет b.
А2. В прямоугольном треугольнике АВС 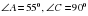 . Найдите
. Найдите 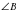 .
.
А3. В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите: а)высоту этого треугольника, проведенную к основанию треугольника; б) площадь треугольника.
А4. Постройте окружность данного радиуса, проходящую через две данные точки.
__________________________________________________
В1. В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон АВ, ВС и СА в точках DE и F соответственно. Известно, что 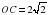 .
.
Найдите: а) радиус окружности; б) углы EOF и EDF.
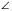 А = 30о, а перпендикуляр ВН к прямой А
А = 30о, а перпендикуляр ВН к прямой А

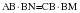 .
.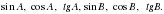
 АСВ = 62°.
АСВ = 62°. 
 . Найдите
. Найдите 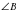 .
.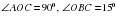 .
. 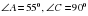 . Найдите
. Найдите 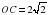 .
. 

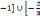



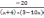
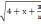

 ;
;

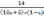
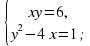
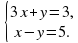
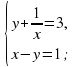
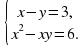
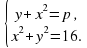 имеет три решения ?
имеет три решения ?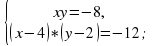
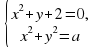 имеет:
имеет: 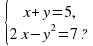
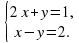
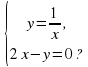
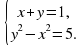
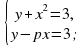 имеет одно решение ?
имеет одно решение ?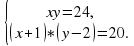
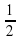 х + 6 и у =
х + 6 и у = 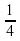 х +
х + 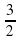 , попарно пересекаясь, образуют треугольник. Вычислите координаты его вершин. Постройте этот треугольник.
, попарно пересекаясь, образуют треугольник. Вычислите координаты его вершин. Постройте этот треугольник.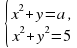 имеет :
имеет :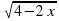 :
: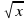 .
.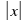 .
.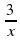 ; 3) у = 5х ; 4) у =
; 3) у = 5х ; 4) у = 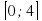 ; г) [4 ; +∞).
; г) [4 ; +∞).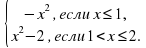
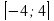 ; Е(
; Е(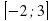 ; у =
; у = 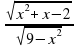 .
.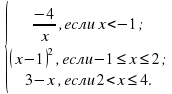
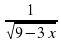
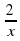 ; 3) у = 3х ; 4) у =
; 3) у = 3х ; 4) у =  .
.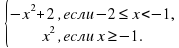
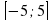 ; Е(
; Е(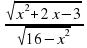 .
.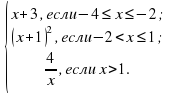
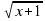 можно получить из графика функции у =
можно получить из графика функции у = 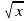 путём:
путём: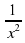 = 4
= 4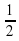 , х2=-2; г) х1=-
, х2=-2; г) х1=-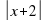 можно получить из графика функции у = х+2 путём:
можно получить из графика функции у = х+2 путём: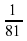 ; б) 81 ; в) 16 ; г)
; б) 81 ; в) 16 ; г) 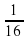 .
. (0 ; 1] ; б) (1 ; +∞) ; в) [1 ; +∞) ; г) нет решений.
(0 ; 1] ; б) (1 ; +∞) ; в) [1 ; +∞) ; г) нет решений.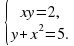
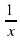 ) 8*
) 8*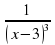 +
+ 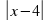 - 1= 0.
- 1= 0. 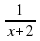 можно получить из графика функции у =
можно получить из графика функции у = 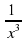 = -х2 .
= -х2 .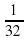 ; г) -32.
; г) -32.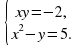
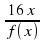 3*
3*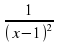 –
– 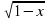 = 0.
= 0.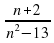 ;
;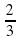 ; б)
; б) 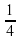 ; в) -
; в) -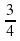 . Её семнадцатый член равен:
. Её семнадцатый член равен: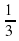 ; в) -12
; в) -12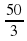 .
.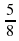 , а
, а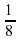 ; г) -
; г) -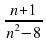 :
: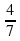 ; в) -
; в) - 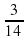 .
.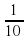 ; в) 0,1 ; г) -0,1 .
; в) 0,1 ; г) -0,1 .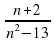 ;
;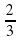 ; б)
; б) 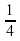 ; в) -
; в) -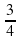 . Её семнадцатый член равен:
. Её семнадцатый член равен: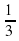 ; в) -12
; в) -12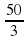 .
.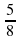 , а
, а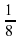 ; г) -
; г) -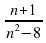 :
: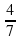 ; в) -
; в) - 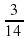 .
.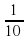 ; в) 0,1 ; г) -0,1 .
; в) 0,1 ; г) -0,1 .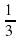 . Укажите формулу
. Укажите формулу 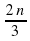 ; б)
; б) 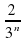 ; в)
; в) 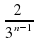 ; г)
; г) 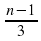 .
. 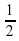 .
.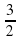 , … . Найдите номер члена этой прогрессии, равного
, … . Найдите номер члена этой прогрессии, равного 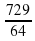 .
.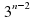 .
.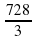 ; б)
; б) 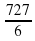 ; в)
; в) 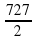 ; г)
; г) 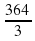 .
.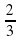 ; г)
; г) 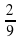 .
.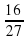 ;
; 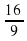 ;
; 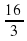 ; … .
; … .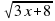 ,
, 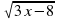 , 1 являются тремя последовательными членами геометрической прогрессии .
, 1 являются тремя последовательными членами геометрической прогрессии .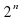 ; в)
; в) 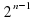 ; г)
; г) 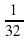 .
.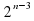 .
.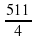 ; г)
; г) 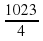 .
.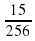 ;
; 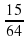 ;
; 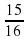 ; … .
; … .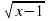 ,
, 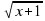 ,
,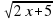 являются тремя последовательными членами геометрической прогрессии.
являются тремя последовательными членами геометрической прогрессии.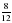 ; б)
; б) 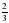 .
.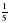 книги. Сколько страниц в книге?.
книги. Сколько страниц в книге?.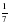 которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами
которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами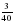 собственной скорости катера?
собственной скорости катера?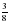 диаметра первой. Начертите эти окружности.
диаметра первой. Начертите эти окружности.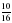 ; б)
; б) 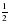 .
. книги. Сколько страниц прочитал мальчик?
книги. Сколько страниц прочитал мальчик?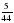 собственной скорости катера?
собственной скорости катера?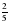 диаметра второй окружности. Начертите эти окружности.
диаметра второй окружности. Начертите эти окружности.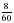 .
.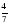 которой занята под помидоры, составляет 140 а. Найдите площадь, занятую помидорами.
которой занята под помидоры, составляет 140 а. Найдите площадь, занятую помидорами.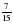 книги. Сколько страниц в книге?
книги. Сколько страниц в книге?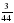 собственной скорости теплохода?
собственной скорости теплохода?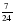 диаметра первой. Начертите эти окружности.
диаметра первой. Начертите эти окружности.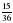 ; б)
; б) 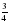 .
.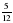 всей площади огорода. Найдите площадь огорода.
всей площади огорода. Найдите площадь огорода.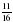 книги. Сколько страниц прочитал мальчик?
книги. Сколько страниц прочитал мальчик?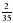 собственной скорости катера?
собственной скорости катера?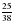 диаметра второй окружности. Начертите эти окружности.
диаметра второй окружности. Начертите эти окружности.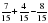 ; б)
; б) 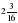 +
+ 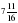 –
– 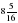 .
.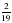 5; б)
5; б) 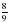 : 3.
: 3.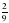 числа всех пар обуви, во второй –
числа всех пар обуви, во второй – 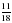 . Какая часть обуви была продана в третий день?
. Какая часть обуви была продана в третий день?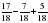 ; б) 3
; б) 3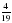 – 1
– 1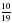 .
.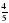 : 7; б)
: 7; б) 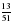
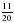 всей работы. Какую часть работы осталось выполнить бригаде?
всей работы. Какую часть работы осталось выполнить бригаде?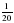 часть котлована, а второй –
часть котлована, а второй – 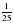 . Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно?
. Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно? 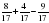 ; б)
; б) 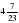 –
– 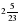 +
+ 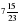 .
.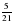 4; г)
4; г) 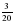 : 5.
: 5.















