Сыныбы: 11
П?ні: Алгебра
Саба?ты? та?ырыбы : Ньютон-Лейбниц формуласы.
Саба?ты? ма?саты: 1) Ньютон-Лейбниц формуласы ж?не оларды шешу т?сілдері туралы т?сінік ;
2) Ньютон-Лейбниц формуласы ж?не шешімін аны?тауды ме?герту;
3)П?нге ?ызы?ушылы?ын арттыра отырып ?з бетімен е?бектенуге, ізденіске баулу ;
Саба? т?рі: жа?а білімді ме?герту.
?дісі: т?сіндіру, салыстыру, тірек-сызба, жатты?у.
?олдан?ан к?рнекіліктер: слаид, тірек-сызба.
Жоспары:
1.?йымдастыру кезе?і.
2.?й тапсырмасын тексеру,?айталау.
3.Жа?а саба?ты т?сіндіру.
4.Білімді бекіту.
5.Саба?ты ?орыту.
6.?йге тапсырма.
Барысы:
1.?йымдастыру кезе?і.
О?ушылармен амандасып,т?гендеу.Саба?ты? ма?саты туралы т?сінік.
2.?й тапсырмасын тексеру,?ткенді ?айталау.
3.Жа?а саба?ты т?сіндіру.
Ньютон-Лейбниц формуласы.
?здiксiз функция ?шiн
м?нда?ы, F(x) – f(x) функциясыны? ал?аш?ы функциясы.
1-мысал. y=sinx, y=cosx, x=0 сызы?тарымен шектелген фигураны? ауданын табы?ыз.
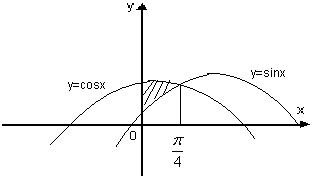
Шешуі: y=sinx, y=cosx функцияларыны? графиктеріні? ?иылысу н?ктелерін табамыз:
(4) формуланы ?олданса?, онда ізделінді аудан аны?тал?ан интеграл ар?ылы былайша аны?талады:
Жауабы: А).
А) ; В) ; С) ; D) ; Е)
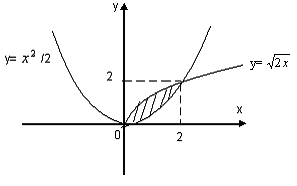
2-мысал. y=, y= сызы?тарымен шектелген фигураны? ауданын табы?ыз.
Шешуі: y= функциясыны? аны?талу облысы x[0;+∞). Функцияны? графиктеріні? ?иылысу н?ктелерін табамыз:
(4) формуланы ?олданса?, онда ізделінді аудан аны?тал?ан интеграл ар?ылы былайша аны?талады:
Жауабы: D).
А) ; В) ; С) ; D) ; Е).
3-мысал. y=, y=1, y=0, x=0 сызы?тарымен шектелген фигураны? ауданын табы?ыз.
Шешуі: Егер фигура y=c, y=d (c<d) т?зулерімен, oy осімен ж?не ?здіксіз ?спелі (кемімелі) y=f(x) (x≥0) функцияны? графигімен шектелген болса, онда оны? ауданы аны?тал?ан интеграл ар?ылы былайша аны?талады:
(5)
м?нда?ы - y=f(x) функциясына кері функция.
функциясына кері функцияны табайы?: x=, - функциясы y= функциясына кері функция.
(5) формуланы ?олданса?, онда ізделінді аудан аны?тал?ан интеграл ар?ылы былайша аны?талады:
Жауабы: С).
А) ; В) ; С) ; D) ; Е) 1.
4-мысал. а параметріні? ?андай м?нінде интеграл максимум м?нін ?абылдайды?
Ш е ш у і. Ньютон-Лейбниц формуласын ?олданып табатынымыз: Сонда бол?анда, интеграл ?зіні? максимум м?ні -ді ?абылдайтынды?ы ай?ын.
Демек, параметр а-ны? ізделінді м?ні -ге те?.
Жауабы: А) .
A) ; B) ; C) ; D) ; E).
5-мысал. Параметр а-ны? ?андай м?ндерінде те?дігі орындалады?
Ш е ш у і. Ньютон-Лейбниц формуласын ?олданып табатынымыз: ; Есепті? шарты бойынша: Б?дан немесе
Демек, параметр а-ны? ізделінді м?ндері -3-ке немесе 1-ге те?.
Жауабы: Е) немесе.
A) ; B) ; C) ; D) ; E) немесе. 4.Білімді бекіту. Тест есептерін шы?ару.
1. ж?не сызы?тарымен шектелген фигураны? ауданын табы?ыз:
А) ; В) ; С); D) ; Е).
2. y=1-x2 ж?не y=0 сызы?тармен шектелген фигураны? ауданын табы?ыз:
А) 2,5; В) 4/3; С) 10/3; D) 5/3; Е) 7/3.
3. Мына сызы?тармен шектелген фигураны? ауданын табы?ыз:
А) 1,5; В) 2,5; С) 3,5; D) 4,5; Е) 5,5.
4. Мына сызы?тармен шектелген ?исы? сызы?ты абсцисса осiнен айналдыра б?р?анда шы?атын дененi? к?лемiн табы?ыз: y=x2, x=1, x=2, y=0
А) ; В) ; С) 2p; D) ; Е).
5. интегралын есепте?із:
А) ; В) 0; С) 1; D) ; Е).
6. Мына сызы?тармен шектелген фигураны? ауданын табы?ыз: y=x2+5x+4, y=3x+4
А) 2; В) ; С) ; D) ; Е).
7. Мына сызы?тармен шектелген ?исы? сызы?ты абсцисса осiнен айналдыра б?р?анда шы?атын дененi? к?лемiн табы?ыз:
А) 7p; В) 9p С) 6p; D) 8p; Е) 5p.
5.Саба?ты ?орыту. Б?гінгі саба?тан т?йген ойлары мен т?жырымдарына байланысты кері байланыс жасайды. Бірін-бірі ба?алайды.
6.?йге тапсырма. О?улы?та?ы есептер ж?не тест есептері.
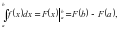
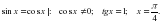
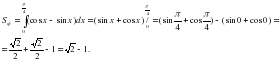
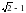 .
.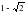 ; С)
; С) 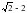 ; D)
; D) 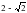 ; Е)
; Е) 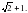
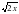 , y=
, y=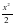 сызықтарымен шектелген фигураның ауданын табыңыз.
сызықтарымен шектелген фигураның ауданын табыңыз. [0;+∞). Функцияның графиктерінің қиылысу нүктелерін табамыз:
[0;+∞). Функцияның графиктерінің қиылысу нүктелерін табамыз: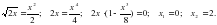
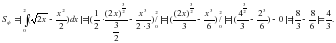
 .
. ; В)
; В) 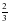 ; С)
; С) 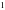 ; D)
; D) 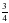 .
.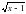 , y=1, y=0, x=0 сызықтарымен шектелген фигураның ауданын табыңыз.
, y=1, y=0, x=0 сызықтарымен шектелген фигураның ауданын табыңыз.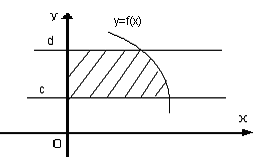
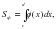 (5)
(5)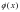 - y=f(x) функциясына кері функция.
- y=f(x) функциясына кері функция.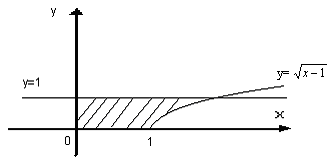
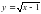 функциясына кері функцияны табайық: x=
функциясына кері функцияны табайық: x=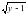 ,
, 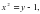
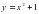 - функциясы y=
- функциясы y=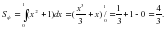
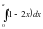 максимум мәнін қабылдайды?
максимум мәнін қабылдайды?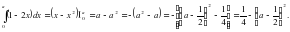 Сонда
Сонда 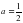 болғанда, интеграл өзінің максимум мәні
болғанда, интеграл өзінің максимум мәні 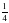 -ді қабылдайтындығы айқын.
-ді қабылдайтындығы айқын.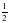 -ге тең.
-ге тең. 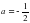 ; C)
; C) 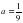 ; D)
; D) 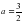 ; E)
; E) 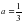 .
.















