Саба?ты? та?ырыбы: Кері тригонометриялы? те?деу мен те?сіздіктер. Саба?ты? ма?саты: Білімділік кері тригонометриялы? те?деу, те?сіздіктерді шеше білуге ?йрету. Дамытушылы?: о?ушыларды? ойлау ?абілеттерін дамыту, ми ж?мысыны? ікерлігін арттыру. Т?рбиелік: ??ыптылы??а, жина?талы??а, тап?ырлы??а т?рбиелеу. Саба?ты? т?рі: жа?а саба?. Саба?ты? ?ту ?дісі: ?жымды?, даралап о?ыту.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Кері тригонометриялы? те?деу ж?не те?сіздіктер
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Кері тригонометриялы? те?деу ж?не те?сіздіктер »
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
2000 руб.
2860 руб.
2020 руб.
2880 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

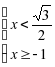
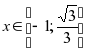 .
.















