| №п/п | Кол-во час | Календ.сроки | Тема урока | КЭС |
| КПУ | | Метапредметные результаты | Дом.задание |
-
|
|
| Тригонометрические уравнения и нера-венства. Преобразование тригономет-рических выражений. | 1.4.4., 2.1.4 |
| 1.3., 2.1. | Проводить преобразования тригонометрическ. выражений, решать уравнения |
|
|
-
|
|
| Тригонометрические уравнения и нера-венства. Преобразование тригономет-рических выражений. | 1.4.4., 2.1.4 |
| 1.3., 2.1. | П. |
|
|
-
|
|
| Производная. Примеры использования производной в прикладных задачах. | 4.1, 4.2 |
| 3.2, 3.3 | Вычислять производные функций, исследовать функции на монотонность и т. д. |
|
|
-
|
|
| Производная. Примеры использования производной в прикладных задачах. | 4.1, 4.2 |
| 3.2, 3.3 | тест №4 |
|
|
-
|
|
| Вводный контроль. |
|
|
|
|
|
|
-
|
|
| Входной срез |
|
|
|
|
|
|
-
|
|
| §1. Многочлены от одной переменной Арифметические операции над многочленами от одной переменной, п. 1 | 1.4.1., 1.4.2. | Стандартный вид многочлена, степень многочлена, корень многочлена. Деление многочлена на многочлен «уголком», теорема Безу, разложение многочлена на линейные множители. | 1.1.-1.3 | Складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители многочлены от одной и нескольких переменных |
|
|
-
|
|
| Деление многочлена на многочлен с остатком, п. 2 |
| Схема Горнера, ее применение для разложения многочлена на множители. |
|
|
|
|
-
|
|
| Разложение многочлена на множители, п. 3 |
| Разложение многочленов с несколькими переменными на множители, стандартный вид, корни многочлена с несколькими переменными. |
|
|
|
|
-
|
|
|
|
| Построение графиков уравнений с двумя переменными, решение систем уравнений. |
|
|
|
|
-
|
|
| Разложение многочлена на множители, п. 3 |
| Симметрические и однородные многочлены. |
|
|
|
|
-
|
|
| §2. Многочлены от нескольких переменных | 1.4.1., 1.4.2. |
| 1.1.-1.3 |
|
|
|
-
|
|
| §2. Многочлены от нескольких переменных |
|
|
|
|
|
|
-
|
|
| §2. Многочлены от нескольких переменных |
|
|
|
|
|
|
-
|
|
| §2. Многочлены от нескольких переменных |
|
|
|
|
|
|
-
|
|
| §3. Уравнения высших степеней | 1.4.1., 1.4.2. | Виды уравнений высших степеней, методы их решения. |
| Применять метод разложения на множители и метод введения новой переменной для уравнений высших степеней |
|
|
-
|
|
| §3. Уравнения высших степеней | 1.4.1., 1.4.2. | Развитие умения определять вид уравнения и применять наиболее рациональные методы к его решению. |
|
|
|
|
-
|
|
| §3. Уравнения высших степеней | 1.4.1., 1.4.2. | Закрепление умения решать уравнения высших степеней различными методами. Подготовка к контрольной работе. |
|
|
|
|
-
|
|
| §3. Уравнения высших степеней | 1.4.1., 1.4.2. | . |
|
|
|
|
-
|
|
| Контрольная работа № 1 по теме: «Многочлены», §§ 1 – 3 | 1.4.1., 1.4.2. | Проверка уровня ЗУН по данной теме |
|
|
|
|
-
|
|
| Контрольная работа № 1 по теме: «Многочлены», §§ 1 – 3 | 1.4.1., 1.4.2. | Проверка уровня ЗУН по данной теме |
|
|
|
|
-
|
|
| §5 16 часов Многогранники Двугранные углы.Многранные углы. |
|
|
|
|
|
|
-
|
|
| Многогранники.Призмы |
|
|
|
|
|
|
-
|
|
| Сечения многогранников. |
|
|
|
|
|
|
-
|
|
|
|
|
|
|
|
|
|
-
|
|
| Площади сечений и поверхностей призм. |
|
|
|
|
|
|
-
|
|
| Параллелепипеды. Прямоугольные параллелепипеды .Куб |
|
|
|
|
|
|
-
|
|
| Параллелепипеды. Прямоугольные параллелепипеды .Куб |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 1 |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 1 |
|
|
|
|
|
|
-
|
|
| Площади поверхностей пирамид. |
|
|
|
|
|
|
-
|
|
| Площади поверхностей пирамид |
|
|
|
|
|
|
-
|
|
| Усеченные пирамиды. |
|
|
|
|
|
|
-
|
|
| Усеченные пирамиды. |
|
|
|
|
|
|
-
|
|
| Правильные многогранники |
|
|
|
|
|
|
-
|
|
| Правильные многогранники |
|
|
|
|
|
|
-
|
|
|
ГЛАВА 2. СТЕПЕНИ И КОРНИ. СТЕПЕННЫЕ ФУНКЦИИ
§4. Понятие корня n-й степени из действительного числа | 1.1.5 | Анализ ошибок, допущенных в контрольной работе. Ввести понятие корня n-й степени. | 3.1., 3.3. | Описывать новую математическую модель. Строить график функции. Исследовать график функции на монотонность, экстремумы, наибольшее и наименьшее значения, четность, ограниченность, непрерывность, выпуклость3.1., 3.3 |
|
|
-
|
|
| §4. Понятие корня n-й степени из действительного числа |
| Ввести понятие функции, рассмотреть ее свойства и график. |
|
|
|
|
-
|
|
| §5. Функции 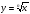 , их свойства и графики , их свойства и графики |
| Область определения данной функции, решение уравнений содержащих знак радикала графическим способом. |
|
|
|
|
-
|
|
| §5. Функции 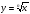 , их свойства и графики , их свойства и графики |
| Доказательство свойств для неотрицательных значений переменных. |
|
|
|
|
-
|
|
| §5. Функции 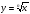 , их свойства и графики , их свойства и графики |
| Доказательство свойств для неотрицательных значений переменных. |
|
|
|
|
-
|
|
| §5. Функции 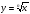 , их свойства и графики , их свойства и графики |
| Отработка навыка применения свойств корней n-й степени |
|
|
|
|
-
|
|
| §6. Свойства корня n-й степени | 1.1.5,1.4.3. | Отработка навыка использования свойств корней n-й степени преобразований выражений. | 1.3 |
|
|
|
-
|
|
| §6. Свойства корня n-й степени |
| Отработка навыка использования свойств корней n-й степени преобразований выражений. |
|
|
|
|
-
|
|
| §6. Свойства корня n-й степени |
| Отработка навыка использования свойств корней n-й степени преобразований выражений. |
|
|
|
|
-
|
|
| §6. Свойства корня n-й степени |
| Отработка навыка использования свойств корней n-й степени преобразований выражений. |
|
|
|
|
-
|
|
| §7. Преобразование выражений, содержащих радикалы |
| Проверка уровня ЗУН по данной теме. |
| Применять свойства извлечения корня при преобразова-нии иррациональ-ных выражений |
|
|
-
|
|
| Преобразование выражений, содержащих радикалы. Внесение множителя под знак радикала |
|
|
|
|
|
|
-
|
|
| Преобразование выражений, содержащих радикалы. Внесение множителя под знак радикала |
| Анализ ошибок, допущенных в контрольной работе. Ввести понятие степени с рациональным показателем. |
|
|
|
|
-
|
|
| Преобразование выражений, содержащих радикалы. Вынесение множителя из под знака радикала |
| Свойства степени. Разложение на множители. |
|
|
|
|
-
|
|
| Преобразование выражений, содержащих радикалы. Вынесение множителя из под знака радикала |
| Преобразование выражений, используя ФСУ. Сравнение чисел, используя свойства степени. |
|
|
|
|
-
|
|
| Контрольная работа № 2 по теме: «Корень n-ой степени и его свойства», §§ 4 – 7 |
| Ввести понятие степенной функции, рассмотреть ее свойства, формулу производной степенной функции. |
|
|
|
|
-
|
|
| Контрольная работа № 2 по теме: «Корень n-ой степени и его свойства», §§ 4 – 7 | | Графическое решение уравнений и неравенств, используя свойства монотонности. |
|
|
|
|
-
|
|
| §8. Понятие степени с любым рациональным показателем | 1.1.7.,3.3.4 | Исследование функций на монотонность и экстремумы. | 3.1., 3.33.1., 3.3 |
|
|
|
-
|
|
| §8. Понятие степени с любым рациональным показателем |
| Познакомить с формулами приближенного вычислений значений степенной функции. |
|
|
|
|
-
|
|
| §8. Понятие степени с любым рациональным показателем |
| Определение корня n-й степени из комплексного числа. Решение уравнений третей степени. |
|
|
|
|
-
|
|
| §8. Понятие степени с любым рациональным показателем |
| Закрепить умения извлечения корня n-й степени из комплексного числа. Решение уравнений третей степени. |
|
|
|
|
-
|
|
| §9. Степенные функции, их свойства и графики |
| Ввести понятие степенной функции, рассмотреть ее свойства, формулу производной степенной функции. |
| Описывать новую математическую модель. Строить график функции. Исследовать график функции на монотонность, экстремумы, наибольшее и наименьшее значения, четность, ограниченность, непрерывность, выпуклость |
|
|
-
|
|
| §9. Степенные функции, их свойства и графики |
| Графическое решение уравнений и неравенств, используя свойства монотонности. |
|
|
|
|
-
|
|
| §9. Степенные функции, их свойства и графики |
| Исследование функций на монотонность и экстремумы. |
|
|
|
|
-
|
|
| §9. Степенные функции, их свойства и графики |
|
|
|
|
|
|
-
|
|
| §9. Степенные функции, их свойства и графики |
|
|
|
|
|
|
-
|
|
| §10. Извлечение корней из комплексных чисел |
| Познакомить с формулами приближенного вычислений значений степенной функции. |
|
|
|
|
-
|
|
| §10. Извлечение корней из комплексных чисел |
| Определение корня n-й степени из комплексного числа. Решение уравнений третей степени. |
|
|
|
|
-
|
|
| §10. Извлечение корней из комплексных чисел |
| Закрепить умения извлечения корня n-й степени из комплексного числа. Решение уравнений третей степени. |
|
|
|
|
-
|
|
| Контрольная работа № 3 по теме: «Степенная функция», §§ 8 – 10 |
| Проверка уровня ЗУН по данной теме. |
|
|
|
|
-
|
|
| Контрольная работа № 3 по теме: «Степенная функция», §§ 8 – 10 | 1.1.7.,3.3.4 |
| 3.1., 3.3 |
|
|
|
-
|
|
| Контрольная работа № 2 |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 2 |
|
|
|
|
|
|
-
|
|
| «Цилиндр» |
|
|
|
|
|
|
-
|
|
|
|
|
|
|
|
|
|
-
|
|
| «Цилиндр» |
|
|
|
|
|
|
-
|
|
| Понятие конуса. Площадь поверхности конуса п. 55-56 |
|
|
|
|
|
|
-
|
|
| Понятие конуса. Площадь поверхности конуса п. 55-56 |
|
|
|
|
|
|
-
|
|
| Усеченный конус, п. 57 |
|
|
|
|
|
|
-
|
|
| Решение задач по теме «Конус» |
|
|
|
|
|
|
-
|
|
| Сфера и шар. Сечения.Касание. |
|
|
|
|
|
|
-
|
|
| Сфера и шар. Сечения.Касание. |
|
|
|
|
|
|
-
|
|
| Симметричность шара и сферы. |
|
|
|
|
|
|
-
|
|
| Вписанные и описанные сферы. |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 3 |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 3 |
|
|
|
|
|
|
-
|
|
| §11. Показательная функция, ее свойства и график | 3.3.6. | Определение показательной функции. Ее свойства. | 3.1., 3.3 | Описывать новую математическую модель. Строить график функции, читать график показательной функции |
|
|
-
|
|
| §11. Показательная функция, ее свойства и график | 3.3.6. | График показательной функции. Решение уравнений графическим способом. | 3.1., 3.3 |
|
|
|
-
|
|
| §11. Показательная функция, ее свойства и график | 3.3.6. | Простейшие показательные уравнения. | 3.1., 3.3 |
|
|
|
-
|
|
| §12. Показательные уравнения Показательные уравнения. Метод введение новой переменной | 3.3.6. | Применение свойств показательной функции для решение показательных уравнений. Графическое решение показательных уравнений. | 3.1., 3.3 |
|
|
|
-
|
|
| Показательные уравнения. Метод уравнивания показателей | 2.1.5, 2.2.3 | Приемы решения показательных уравнений. |
|
|
|
|
-
|
|
| Показательные уравнения. Функционально – графический метод |
| Простейшие показательные неравенства. |
|
|
|
|
-
|
|
| Решение показательных уравнений разными методами |
| Способы решения показательных неравенств. |
|
|
|
|
-
|
|
| §13. Показательные неравенства | 2.1.5, 2.2.3 |
|
|
|
|
|
-
|
|
| §13. Показательные неравенства |
|
|
|
|
|
|
-
|
|
| §13. Показательные неравенства |
|
|
|
|
|
|
-
|
|
| §14. Понятие логарифма | 1.3.1, 3.3.7 |
| 3.1., 3.3 |
|
|
|
-
|
|
| §14. Понятие логарифма |
| Ввести понятие логарифма. |
|
|
|
|
-
|
|
| §15. Логарифмическая функция, ее свойства и график |
| Ввести определение логарифмической функции и рассмотреть ее свойства. |
|
|
|
|
-
|
|
| §15. Логарифмическая функция, ее свойства и график |
| Научить строить графики логарифмической функции. |
|
|
|
|
-
|
|
| §15. Логарифмическая функция, ее свойства и график | 1.3.1, 3.3.7 | Решение уравнений графическим способом. | 3.1., 3.3 |
|
|
|
-
|
|
| Контрольная работа № 4 по теме: «Показательная функция. Показательные уравнения и неравенства», §§ 11 – 15 |
| Обобщить и систематизировать знания по теме. |
|
|
|
|
-
|
|
| Контрольная работа № 4 по теме: «Показательная функция. Показательные уравнения и неравенства», §§ 11 – 15 |
| Проверка уровня ЗУН по данной теме. |
|
|
|
|
-
|
|
| §16. Свойства логарифмов | 1.3.2, 1.3.3., 1.4.5 | Анализ ошибок, допущенных в контрольной работе. Основные свойства логарифмов и их применение. | 1.3 |
|
|
|
-
|
|
| Свойства логарифмов. Логарифм произведения и частного |
| Основные свойства логарифмов и их применение. |
|
|
|
|
-
|
|
| Свойства логарифмов. Логарифм произведения и частного |
| Преобразование выражений, содержащих логарифмы. |
|
|
|
|
-
|
|
| Свойства логарифмов. Логарифм степени |
| Десятичный логарифм. |
|
|
|
|
-
|
|
| Свойства логарифмов. Логарифм степени |
| Рассмотреть способы решений логарифмических уравнений. |
|
|
|
|
-
|
|
| §17. Логарифмические уравнения Логарифмические уравнения. Метод потенцирования | 2.1.6, 2.2.4 | Методы логарифмирования. | 2 | Решать уравнения различными методами. Решать неравенства с основанием больше 1 и с основанием от 0 до 1. Применять при решении неравенств особое свойство |
|
|
-
|
|
| Логарифмические уравнения. Метод введение новой переменной |
| Способы решений логарифмических уравнений. |
|
|
|
|
-
|
|
| Логарифмические уравнения. Функционально – графический метод |
| Способы решений логарифмических уравнений. |
|
|
|
|
-
|
|
| Логарифмические уравнения. Метод логарифмирования |
| Рассмотреть метод решения логарифмических неравенств. |
|
|
|
|
-
|
|
| Решение логарифмических уравнений разными методами |
| Графический метод решения логарифмических неравенств. |
|
|
|
|
-
|
|
| Итоговая работа за I полугодие |
|
|
|
|
|
|
-
|
|
| §18. Логарифмические неравенства |
|
|
|
|
|
|
-
|
|
| §18. Логарифмические неравенства |
|
|
|
|
|
|
-
|
|
| §18. Логарифмические неравенства |
|
|
|
|
|
|
-
|
|
| §18. Логарифмические неравенства |
|
|
|
|
|
|
-
|
|
| §19. Дифференцирование логарифмической и показательной функций Число е, функция y=ex, ее свойства, график, дифференцирование, п. 1 | 4.1.5. | Формировать представление о числе ℮. Ввести понятие натурального логарифма. Ввести формулу производной показательной функции. | 3.2 |
|
|
|
-
|
|
| Натуральный логарифм. Функция y=ln x, ее свойства и график, дифференцирование, п. 2 | 4.1.5. | Рассмотреть производную логарифмической функции и научить находить ее. Примеры нахождения производной составных функций. | 3.2 |
|
|
|
-
|
|
| Натуральный логарифм. Функция y=ln x, ее свойства и график, дифференцирование, п. 2 | 4.1.5. | Обобщить и систематизировать знания по теме. | 3.2 |
|
|
|
-
|
|
| Натуральный логарифм. Функция y=ln x, ее свойства и график, дифференцирование, п. 2 |
| . |
|
|
|
|
-
|
|
| Контрольная работа №5 по теме: «Логарифмическая функция. Логарифмические уравнения и неравенства», §§ 16 – 19 | 1.3.2, 1.3.3., 1.4.5, 2.1.6, 2.2.4.,4.1.5. | Проверка уровня ЗУН по данной теме | 1.3, 2, 3.2 |
|
|
|
-
|
|
| Контрольная работа №5 по теме: «Логарифмическая функция. Логарифмические уравнения и неравенства», §§ 16 – 19 |
| Проверка уровня ЗУН по данной теме |
|
|
|
|
-
|
|
| §20. Первообразная и неопределенный интеграл Определение первообразной, п. 1 | 4.3.1. | Анализ ошибок, допущенных в контрольной работе. Ввести понятие первообразной. Рассмотреть признак постоянства функции, основные свойства первообразных и его геометрический смысл. | 3.2 |
|
|
|
-
|
|
| Правила отыскания первообразных, п. 2 |
| Примеры нахождения первообразных. Формулировка правил. Выработка умений находить первообразные, применяя три правила. |
|
|
|
|
-
|
|
| Правила отыскания первообразных, п. 2 |
|
|
|
|
|
|
-
|
|
| Неопределенный интеграл, п. 3 |
| Ввести понятие интеграл. Понятие о определенном интеграле. |
|
|
|
|
-
|
|
| §21. Определенный интеграл Задачи, приводящие к понятию определенного интеграла, п. 1 | 4.3.2. | Продолжить отрабатывать понятие интеграла, формировать умение вычислять определенный интеграл. | 3.2 |
|
|
|
-
|
|
| Понятие определенного интеграла, п. 2 | 4.3.2. | Показать примеры применения формулы Ньютона-Лейбница. | 3.2 |
|
|
|
-
|
|
| Формула Ньютона – Лейбница, п. 3 | 4.3.2. | Ввести понятие криволинейной трапеции и формулу вычисления ее площади. | 3.2 |
|
|
|
-
|
|
| Формула Ньютона – Лейбница, п. 3 | 4.3.2. | Обобщить и систематизировать знания по теме. | 3.2 |
|
|
|
-
|
|
| Вычисление площадей плоских фигур с помощью определенного интеграла, п. 4 | 4.3.2. | . | 3.2 |
|
|
|
-
|
|
| Вычисление площадей плоских фигур с помощью определенного интеграла, п. 4 | 4.3.2. |
| 3.2 |
|
|
|
-
|
|
| Контрольная работа № 6 по теме: «Первообразная и интеграл», §§ 20 – 21 |
| Проверка уровня ЗУН по данной теме |
|
|
|
|
-
|
|
| ГЛАВА VII. ОБЪЕМ ТЕЛ § 7. Объемы многогранников |
|
|
|
|
|
|
-
|
|
| Понятие объема. Объем прямоугольного параллелепипеда, п. 63 |
|
|
|
|
|
|
-
|
|
| Объем прямой призмы, основанием которой является прямоугольный треугольник, п. 64 |
|
|
|
|
|
|
-
|
|
| Объем прямой призмы, основанием которой является прямоугольный треугольник, п. 64 |
|
|
|
|
|
|
-
|
|
| Объем пирамид |
|
|
|
|
|
|
-
|
|
| Объем пирамид |
|
|
|
|
|
|
-
|
|
| Объем усеченных пирамид Повторение вопросов теории и решение задач |
|
|
|
|
|
|
-
|
|
| Объем усеченных пирамид Повторение вопросов теории и решение задач |
|
|
|
|
|
|
-
|
|
| Контрольная работа №4 |
|
|
|
|
|
|
-
|
|
| Контрольная работа №4 |
|
|
|
|
|
|
-
|
|
| Объемы цилиндров и конусов. |
|
|
|
|
|
|
-
|
|
| Объемы цилиндров и конусов. |
|
|
|
|
|
|
-
|
|
| Площади поверхностей цилиндров и конусов |
|
|
|
|
|
|
-
|
|
| Площади поверхностей цилиндров и конусов |
|
|
|
|
|
|
-
|
|
| Объем шара, п. 71 |
|
|
|
|
|
|
-
|
|
| Объем шарового сегмента, шарового слоя и шарового сектора, п.72 |
|
|
|
|
|
|
-
|
|
| Повторение |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 5 |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 5 |
|
|
|
|
|
|
-
|
|
| ГЛАВА 5. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСК. СТАТИСТИКИ §22. Вероятность и геометрия | 6.3.1., 6.3.2. | Классическое определение вероятности. | 6 |
|
|
|
-
|
|
| §23. Независимые повторения испытаний с двумя исходами | 6.3.1., 6.3.2. | Правило нахождения геометрических вероятностей. | 6 | Применять классическую вероятностную схему и схему Бернулли при решении вероятностных задач |
|
|
-
|
|
| §23. Независимые повторения испытаний с двумя исходами | 6.3.1., 6.3.2. | Схема Бернулли. | 6 |
|
|
|
-
|
|
| §23. Независимые повторения испытаний с двумя исходами | 6.3.1., 6.3.2. | Алгоритм вычисления вероятности «успеха». | 6 |
|
|
|
-
|
|
| §23. Независимые повторения испытаний с двумя исходами | 6.3.1., 6.3.2. | Отработка навыков вычисления вероятности. | 6 |
|
|
|
-
|
|
| §23. Независимые повторения испытаний с двумя исходами | 6.3.1., 6.3.2. |
| 6 |
|
|
|
-
|
|
| §24. Статистические методы обработки информации | 6.2.1., 6.2.2. | Обработка информации, ее порядок, таблица распределения кратностей данных измерения | 6 |
|
|
|
-
|
|
| §24. Статистические методы обработки информации |
| Процентная частота варианты, среднее квадратичное отклонение. |
|
|
|
|
-
|
|
| §24. Статистические методы обработки информации |
| Понятие статистической устойчивости, функция Гаусса. |
|
|
|
|
-
|
|
| §25. Гауссова кривая. Закон больших чисел |
| Алгоритм использования функции в приближенных вычислениях. |
|
|
|
|
-
|
|
| §25. Гауссова кривая. Закон больших чисел |
|
|
|
|
|
|
-
|
|
| ГЛАВА 6. УРАВНЕНИЯ И НЕРАВЕНСТВА. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ §26. Равносильность уравнений Теоремы о равносильности уравнений, п. 1 | 2.1.7 | Анализ ошибок, допущенных в контрольной работе. Понятие равносильности уравнений, следствие уравнения. | 5.3 | Выполнять тождественные преобразования уравнений, применять теоремы равносильности. |
|
|
-
|
|
| Преобразование данного уравнения в уравнение-следствие, п. 2 | 2.1.7 | Преобразование уравнения в уравнение-следствие. | 5.3 | |
|
|
-
|
|
| О проверке корней, п. 3 | 2.1.7 | Проверка корней, причины потери корней. | 5.3 | |
|
|
-
|
|
| О потере корней, п. 4 | 2.1.7 |
| 5.3 2.1., 2.2. | |
|
|
-
|
|
| §27. Общие методы решения уравнений Замена уравнения h(f(x)) = h(g(x)) уравнением f(x) =g(x), п. 1 | 2.1.1, 2.1.6, 2.1.10 | Метод разложения на множители. |
| Применять общие методы при решении уравнений любых видов |
|
|
-
|
|
| Метод разложения на множители, п. 2 |
| Метод введения новой переменной. |
|
|
|
|
-
|
|
| Метод введения новой переменной, п. 3 |
| Функционально-графический метод. |
|
|
|
|
-
|
|
| Функционально-графический метод, п. 4 |
| Общее и частное решение неравенства. Теоремы о равносильности неравенств. |
|
|
|
|
-
|
|
| §28. Равносильность неравенств | 2.2.7, 2.2.8, 2.2.9 | Раскрытие модуля по определению. | 5.3 |
|
|
|
-
|
|
| §28. Равносильность неравенств | 2.2.7, 2.2.8, 2.2.9 | Графический способ, метод интервалов, переход к системе, совокупности. | 5.3 |
|
|
|
-
|
|
| §28. Равносильность неравенств | 2.2.7, 2.2.8, 2.2.9 | Применение различных способов решения уравнений и неравенств с модулем. | 5.3 |
|
|
|
-
|
|
| §29. Уравнения и неравенства с модулем. Раскрытия модуля по определению | 1.4.6, 2.1.1-2.1.6 | Применение различных способов решения уравнений и неравенств с модулем. |
|
|
|
|
-
|
|
| Уравнения и неравенства с модулем. Раскрытия модуля по определению | 1.4.6, 2.1.1-2.1.6 | Обобщить и систематизировать знания по теме. |
|
|
|
|
-
|
|
| Уравнения и неравенства с модулем. Графический метод | 1.4.6, 2.1.1-2.1.6 | Проверка уровня ЗУН по данной теме |
|
|
|
|
-
|
|
| Уравнения и неравенства с модулем. Графический метод | 1.4.6, 2.1.1-2.1.6 |
|
|
|
|
|
-
|
|
| Контрольная работа № 7 по теме: «Уравнения и неравенства», §§ 26 – 29 |
|
|
|
|
|
|
-
|
|
| Контрольная работа № 7 по теме: «Уравнения и неравенства», §§ 26 – 29 |
|
|
|
|
|
|
-
|
|
| §30. Иррациональные уравнения и неравенства | 2.1.3. | Анализ ошибок, допущенных в контрольной работе. Определение иррациональных уравнений, общие методы решения. | 2 |
|
|
|
-
|
|
| Иррациональные уравнения, п. 1 | 2.1.3. | Специфические приемы решения уравнений и способы проверки корней. | 2 |
|
|
|
-
|
|
| Иррациональные неравенства, п. 2 | 2.1.3. | Равносильность перехода иррациональных неравенств к системе неравенств или их совокупности. | 2 |
|
|
|
-
|
|
| Иррациональные неравенства, п. 2 | 2.2. | Понятие решения уравнения с двумя переменными, диофантовы уравнения и методы их решения. | 5.3 |
|
|
|
-
|
|
| §31. Доказательство неравенств Доказательство неравенств с помощью определения, п. 1. Синтетический метод доказательства неравенств, п. 2 | 2.2. | Некоторые методы доказательства неравенств. | 5.3 |
|
|
|
-
|
|
| Доказательство неравенств методом от противного, п. 3 |
| Некоторые методы доказательства неравенств. |
|
|
|
|
-
|
|
| Доказательство неравенств методом математической индукции, п. 4 |
| Применение различных методов доказательства неравенств. |
|
|
|
|
-
|
|
| Функционально-графические методы доказательства неравенств, п. 5 |
| Равносильность систем уравнений. |
|
|
|
|
-
|
|
| §32. Уравнения и неравенства с двумя переменными | 2.1.112.2.10 | Методы решения систем уравнений. |
|
|
|
|
-
|
|
| §32. Уравнения и неравенства с двумя переменными | 2.1.112.2.10 | Комбинированные системы уравнений. |
|
|
|
|
-
|
|
| §32. Уравнения и неравенства с двумя переменными |
| Системы уравнений с тремя переменными. |
|
|
|
|
-
|
|
| §33. Системы уравнений Системы уравнений. Основные понятия | 2.1.7-2.1.9 | Равносильность систем уравнений. |
|
|
|
|
-
|
|
| Методы решений систем уравнений |
| Методы решения систем уравнений. |
|
|
|
|
-
|
|
| Методы решений систем уравнений |
| Комбинированные системы уравнений. |
|
|
|
|
-
|
|
| Задачи на составление систем уравнений |
| Системы уравнений с тремя переменными. |
|
|
|
|
-
|
|
| Задачи на составление систем уравнений |
|
|
|
|
|
|
-
|
|
|
|
|
|
|
|
|
|
-
|
|
| §34. Задачи с параметрами Уравнения с параметрами | 2.1.12 |
| 5.1, 5.3 | Находить действительные решения уравнений и неравенств с параметром. |
|
|
-
|
|
| Уравнения с параметрами | 2.1.12 |
| 5.1, 5.3 |
|
|
|
-
|
|
| Уравнения с параметрами | 2.1.12 |
| 5.1, 5.3 |
|
|
|
-
|
|
| Уравнения с параметрами | 2.1.12 |
| 5.1, 5.3 |
|
|
|
-
|
|
| Неравенства с параметрами |
| Обобщить и систематизировать знания по теме. |
|
|
|
|
-
|
|
| Контрольная работа № 8 по теме: «Системы уравнений и неравенст§ 30 – 34 |
| Проверка уровня ЗУН по данной теме. |
|
|
|
|
-
|
|
| Контрольная работа № 8 по теме: «Системы уравнений и неравенст§ 30 – 34 |
|
|
|
|
|
|
-
|
|
| Аксиомы стереометрии и их следствия. Параллельность прямых, прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей |
|
|
|
|
|
|
-
|
|
| Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью |
|
|
|
|
|
|
-
|
|
| Двугранный угол. Перпендикулярность плоскостей |
|
|
|
|
|
|
-
|
|
| Многогранники: параллелепипед, призма, пирамида, площади их поверхностей |
|
|
|
|
|
|
-
|
|
| Многогранники: параллелепипед, призма, пирамида, площади их поверхностей |
|
|
|
|
|
|
-
|
|
| Векторы в пространстве. Действия над векторами. Скалярное произведение векторов |
|
|
|
|
|
|
-
|
|
| Цилиндр, конус и шар, площади их поверхностей |
|
|
|
|
|
|
-
|
|
| Объемы тел |
|
|
|
|
|
|
-
|
|
| Объемы тел |
|
|
|
|
|
|
| 212-217 |
|
| Повторение теории и решение задач по всему курсу геометрии |
|
|
|
|
|
|
| 218 |
|
| Производная. Применение производной к решению задач |
|
|
|
|
|
|
| 219 |
|
| Производная. Применение производной к решению задач |
|
|
|
|
|
|
| 220 |
|
| Интеграл. Площадь криволинейной трапеции |
|
|
|
|
|
|
| 221 |
|
| Интеграл. Площадь криволинейной трапеции |
|
|
|
|
|
|
| 222 |
|
| Первообразная. Применение первообразной к решению задач |
|
|
|
|
|
|
| 223 |
|
| Первообразная. Применение первообразной к решению задач |
|
|
|
|
|
|
| 224 |
|
| Контрольная работа № 9 (итоговая работа) |
|
|
|
|
|
|
| 225- |
|
| Контрольная работа № 9 (итоговая работа) |
|
|
|
|
|
|
| 226-238 |
|
| Комплексное повторение основных вопросов курса алгебры 7 – 9 классов, алгебры и начал анализа 10 – 11 классов |
|
|
|
|
|
|
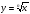 , их свойства и графики
, их свойства и графики















