| № уро ка | Дата по плану | Содержание учебного материала | Тип урока | Вводимые понятия |
Примечание
|
| 1 |
| Повторение | Урок-практикум
|
|
|
| 2 |
| Повторение | Урок-практикум
|
|
|
| Глава 1. Алгебраические дроби. (22) |
| 3 |
| Основные понятия | Урок изложения новой темы | Ввести понятие алгебраической дроби и допустимых значений для дроби; формировать умение определять область допустимых значений для любой дроби. |
|
| 4 |
| Основные понятия | Урок-практикум |
|
|
| 5 |
| Основное свойство алгебраической дроби | Урок изложения новой темы | Основное свойство дроби, рассмотреть это свойство для алгебраических дробей; формировать умение самостоятельно работать с книгой, сокращать дроби и приводить их к общему знаменателю. |
|
| 6 |
| Основное свойство алгебраической дроби | Урок-практикум |
|
|
| 7 |
| Сложение и вычитание алгебраических дробей с одинаковыми знаменателями | Урок изложения новой темы | Правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями; |
|
| 8 |
| Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
| Урок-практикум |
|
|
| 9 |
| Сложение и вычитание алгебраических дробей с разными знаменателями | Урок изложения новой темы | Правила сложения и вычитания алгебраических дробей с разными знаменателями; |
|
| 10 |
| Сложение и вычитание алгебраических дробей с разными знаменателями | Урок-практикум |
|
|
| 11 |
| Сложение и вычитание алгебраических дробей с разными знаменателями | Урок-практикум |
|
|
| 12 |
| Сложение и вычитание алгебраических дробей с разными знаменателями | Урок актуализации знаний. |
|
|
| 13 |
| Контрольная работа №1 | Урок проверки знаний |
|
|
| 14 |
| Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень | Урок изложения новой темы | Умножения и деления числовых дробей; правила умножения и деления алгебраических дробей. Свойства степени и правила возведения в степень алгебраической дроби |
|
| 15 |
| Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень | Урок-практикум |
|
|
| 16 |
| Преобразование рациональных выражений | Урок изложения новой темы | Правила преобразования рациональных выражений |
|
| 17 |
| Преобразование рациональных выражений | Урок-практикум |
|
|
| 18 |
| Преобразование рациональных выражений | Урок актуализации знаний. |
|
|
| 19 |
| Первые представления о решении рациональных уравнений | Урок изложения новой темы |
|
|
| 20 |
| Первые представления о решении рациональных уравнений | Урок-практикум |
|
|
| 21 |
| Степень с отрицательным показателем | Урок изложения новой темы | Свойства степени с натуральным показателем; ввести понятие и свойства степени с отрицательным целым показателем; формировать умение работать со степенями с целым показателем. |
|
| 22 |
| Степень с отрицательным показателем | Урок-практикум |
|
|
| 23 |
| Степень с отрицательным показателем | Урок-практикум |
|
|
| 24 |
| Контрольная работа№2 | Урок проверки знаний |
|
|
| Учащиеся должны: |
| 1 | Знать: -понятие алгебраической дроби; -основное свойство дроби; -описание словами правил умножения и деления алгебраических дробей, возведение алгебраической дроби в степень, сложения и вычитания алгебраических дробей с одинаковыми знаменателями; -понятие общего знаменателя нескольких дробей; -описание словами правила отыскания общего знаменателя нескольких дробей и правило сложения дробей с разными знаменателями; -определение и свойства степени с любым целым показателем; |
| 2 | Уметь: -находить значения алгебраической дроби, находить допустимые и недопустимые значения переменной для данной алгебраической дроби; -применять основное свойство алгебраической дроби; - применять основное свойство алгебраической дроби для сокращения дробей, для приведения дробей к общему знаменателю; -преобразовывать рациональные выражения с использованием правил арифметических операций над алгебраическими дробями; -решать уравнения вида 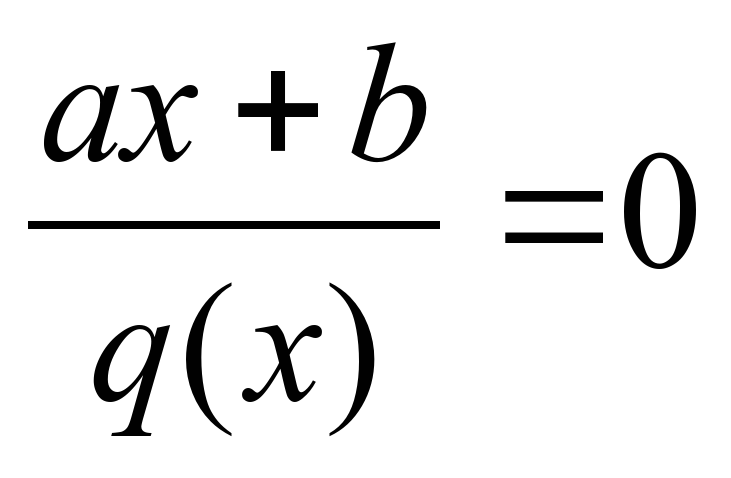 , где q(x)-многочлен, и уравнения, сводящиеся к указанному виду; , где q(x)-многочлен, и уравнения, сводящиеся к указанному виду; -решать соответствующие текстовые задачи; -вычислять а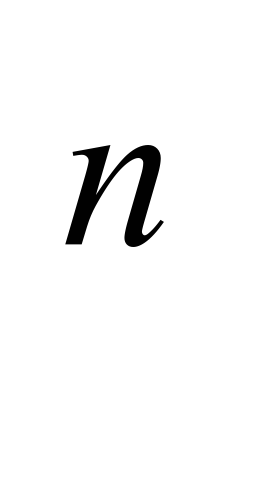 для любых действительных чисел а≠0 и любых целых значений n; для любых действительных чисел а≠0 и любых целых значений n; -использовать свойства степени с целым показателем для вычисления значений арифметических и алгебраических выражений, для преобразования алгебраических выражений, для доказательства тождеств. |
| Глава 2. Функция y=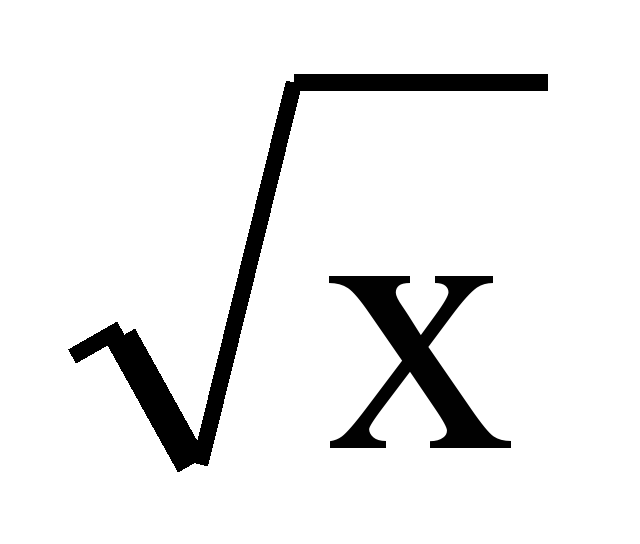 .Свойства квадратного корня (18). .Свойства квадратного корня (18). |
| 25 |
| Рациональные числа | Урок изложения новой темы | Ввести понятие множества натуральных, действительных, рациональных чисел; формировать умение различать множества чисел. |
|
| 26 |
| Рациональные числа | Урок-практикум |
|
|
| 27 |
| Понятие квадратного корня из неотрицательного числа. | Урок изложения новой темы | Ввести понятие квадратного корня, рассмотреть правила вычисления квадратного корня из неотрицательного числа; формировать умение вычислять квадратный корень из чисел и выражений |
|
| 28 |
| Понятие квадратного корня из неотрицательного числа. | Урок-практикум |
|
|
| 29 |
| Иррациональные числа | Урок изложения новой темы | Понятие натуральных, целых и рациональных чисел; закрепить умение переводить периодические дроби в обыкновенные дроби; ввести понятие иррациональных чисел; развивать умение различать множества чисел. |
|
| 30 |
| Множество действительных чисел | Урок изложения новой темы | Понятие натуральных, целых, рациональных и иррациональных чисел; ввести понятие и обозначение множества действительных чисел. |
|
| 31 |
| Функция y=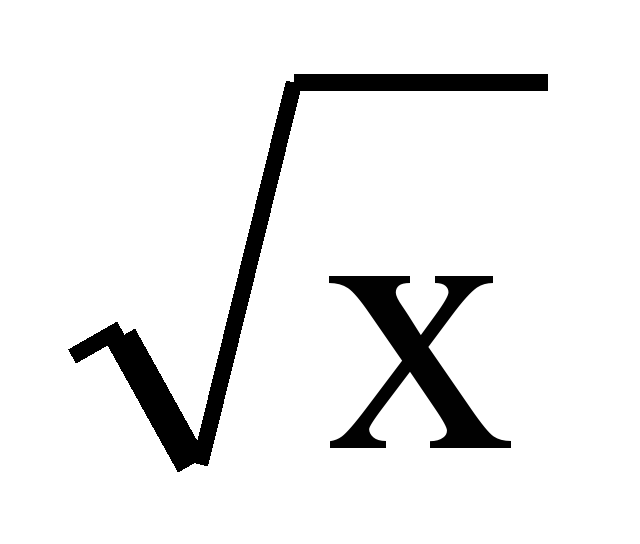 , её свойства и график , её свойства и график | Урок изложения новой темы | Ввести функцию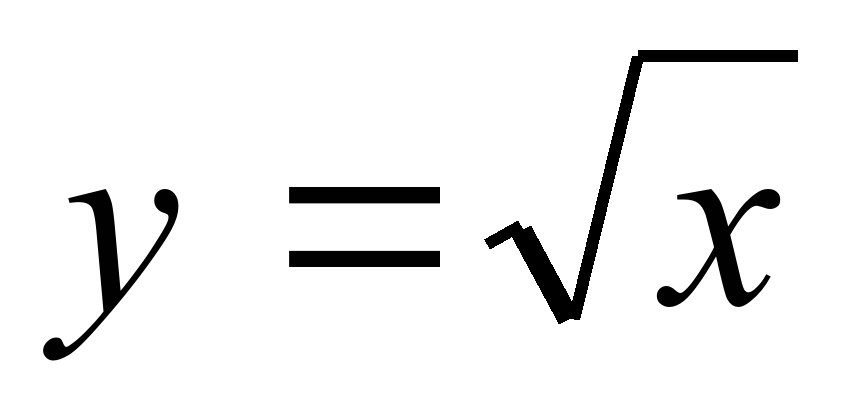 и показать правила построения графика данной функции; ввести понятие выпуклости и области значений; формировать умение строить графики функций вида и показать правила построения графика данной функции; ввести понятие выпуклости и области значений; формировать умение строить графики функций вида 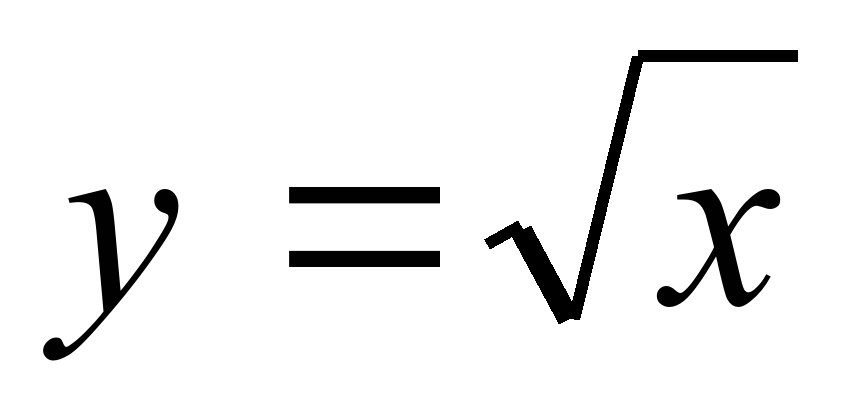 ,и по графику определять свойства функций. ,и по графику определять свойства функций. |
|
| 32 |
| Функция y=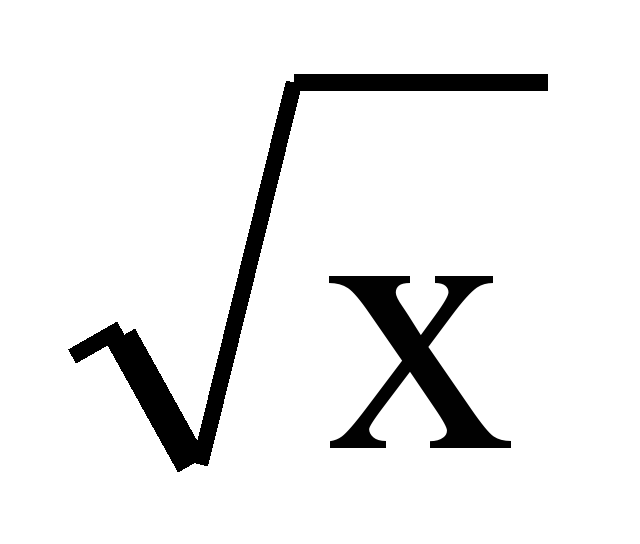 , её свойства и график , её свойства и график | Урок-практикум |
|
|
| 33 |
| Свойства квадратных корней | Урок изложения новой темы | Доказать свойства квадратных корней и показать их применение; формировать умение вычислять квадратные корни, используя их свойства. |
|
| 34 |
| Свойства квадратных корней | Урок-практикум |
|
|
| 35 |
| Преобразование выражений, содержащих операцию извлечения квадратного корня | Урок изложения новой темы | Объяснить правила вынесения множителя из-под знака корня, внесения множителя под знак корня, преобразование подобных членов; рассмотреть примеры на преобразование различной сложности; развивать умение пользоваться свойствами квадратных корней. |
|
| 36 |
| Преобразование выражений, содержащих операцию извлечения квадратного корня | Урок-практикум |
|
|
| 37 |
| Преобразование выражений, содержащих операцию извлечения квадратного корня | Урок-практикум |
|
|
| 38 |
| Преобразование выражений, содержащих операцию извлечения квадратного корня | Урок актуализации знаний. |
|
|
| 39 |
| Контрольная работа №3 | Урок проверки знаний |
|
|
| 40 |
| Модуль действительного числа, график функции у=|х|, формула 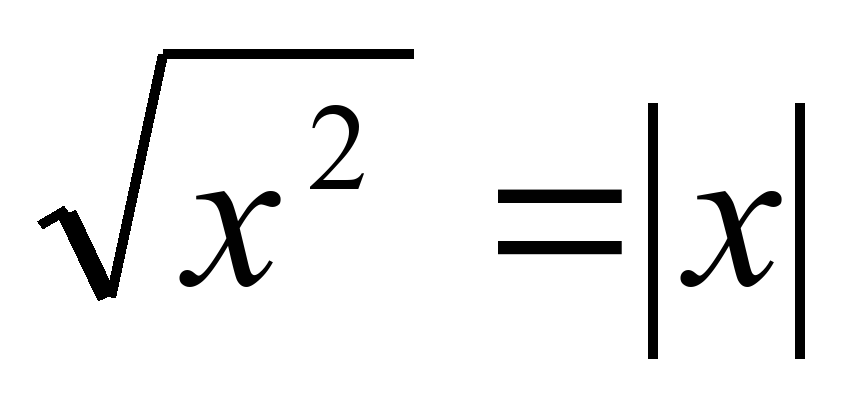 | Урок изложения новой темы | Понятие модуля, правила построения графиков, содержащих функцию у=�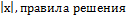 �и оформления уравнений, содержащих модуль; рассмотреть свойство модуля �и оформления уравнений, содержащих модуль; рассмотреть свойство модуля 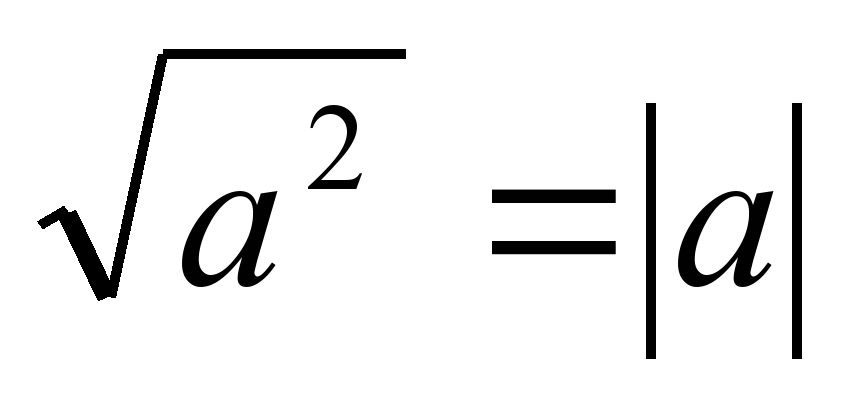 и его значение для упрощения выражений; развивать умение работать с модулем. и его значение для упрощения выражений; развивать умение работать с модулем. |
|
| 41 |
| Модуль действительного числа, график функции у=|х|, формула 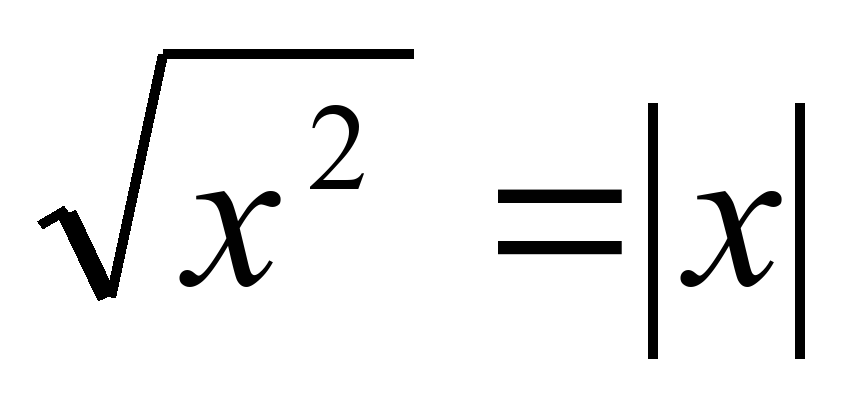 | Урок-практикум |
|
|
| 42 |
| Модуль действительного числа, график функции у=|х|, формула 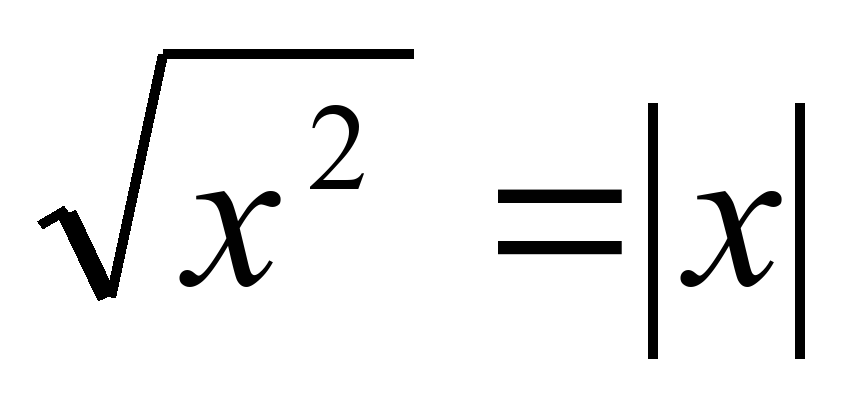 | Урок-практикум |
|
|
| Учащиеся должны: |
| 1 |
Знать: -понятие квадратного корня из неотрицательного числа; -свойства квадратных корней для неотрицательных подкоренных выражений; -график функции y=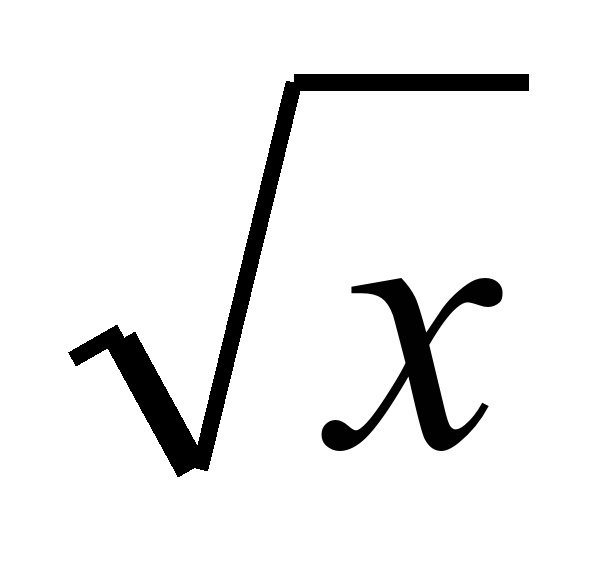 , описание с помощью графика свойств этой функции; , описание с помощью графика свойств этой функции; -представление о рациональных, иррациональных, действительных числах; -истолкование рационального числа как обыкновенной дроби как бесконечной десятичной периодической дроби; -числовую прямую как геометрическую модель множества действительных чисел; -модуль действительного числа, его свойства и геометрический смысл; -функцию y=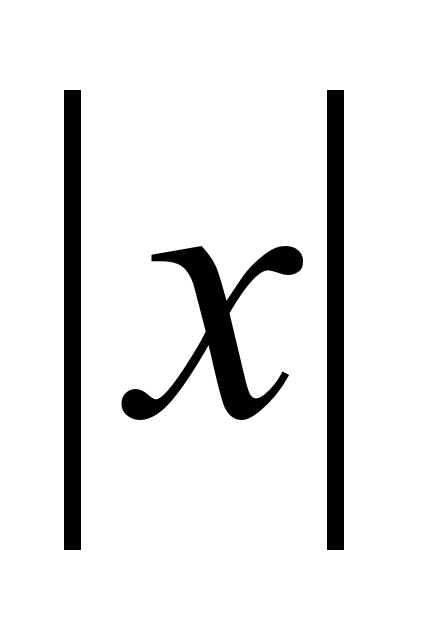 , ее свойства и график; , ее свойства и график; -тождество 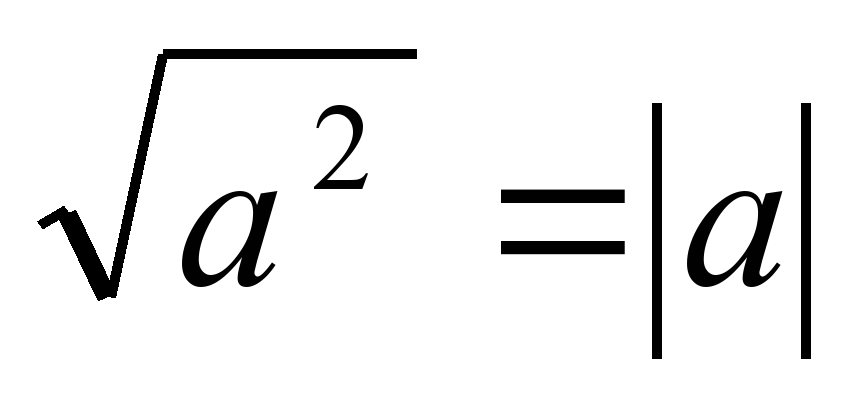 . . |
| 2 | Уметь: -вычислять конкретные значения и строить графики функций у=√х, у= - √х, и функцийу=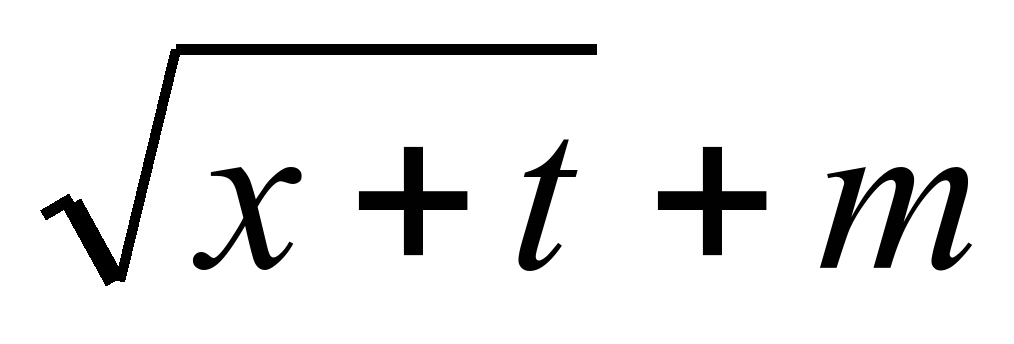 и функций, и и функций заданных различными формулами (включая у=√х) на различных промежутках; и функций, и и функций заданных различными формулами (включая у=√х) на различных промежутках; -графически g(x), решать уравнения вида √х = g(x), где у= g(x)-одна из ранее изученных функций; -находить наибольшее и наименьшее значение функции у=√х на заданных промежутках; -читать график; -решать задачи на функциональную символику; -использовать новые символы математического языка N,Z,Q,R; -приводить примеры рациональных и иррациональных чисел; -сравнивать действительные числа по величине и располагать их в порядке возрастания на числовой прямой; -находить модуль любого действительного числа и использовать геометрический смысл модуля для решения простейших уравнений с модулями; -использовать в несложных случаях формулу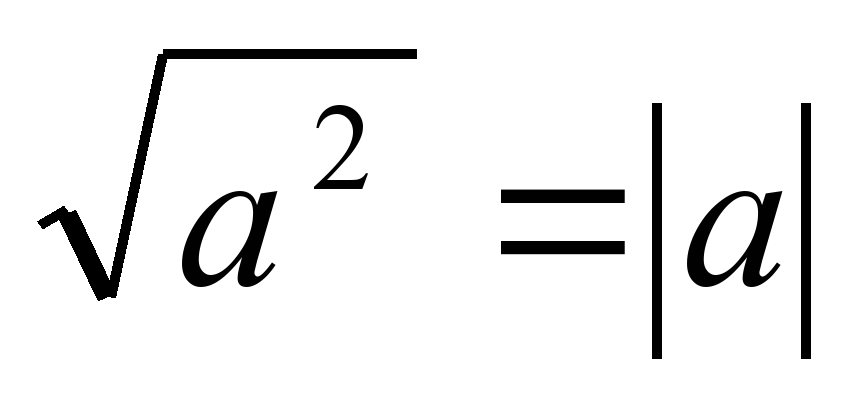 ; ; |
| Глава 3. Квадратичная функция. Функция y= (18) (18) |
|
|
| 43 |
| Функция y=kx2, её свойства и график | Урок изложения новой темы | Свойства функций у= kx +b и у= x2 ,их графики; свойства функции у= kx2 и построение графика данной функции; формировать умение строить графики функций у= kx +b и у= kx2, и по графику определять свойства данных функций. |
|
| 44 |
| Функция y=kx2, её свойства и график | Урок-практикум | Свойствах функции вида у= kx2 и умение строить ее график; ввести правила решения уравнений графическим способом; показать способ построения графиков функций, заданных несколькими условиями; развивать умение строить графики известных функций. |
|
| 45 |
| Функция y=kx2, её свойства и график | Урок-практикум |
|
|
| 46 |
| Функция y= , её свойства и график , её свойства и график | Урок изложения новой темы | Алгоритм графического решения уравнений и систем уравнений; ввести понятие гиперболы; показать правила построения графика функции 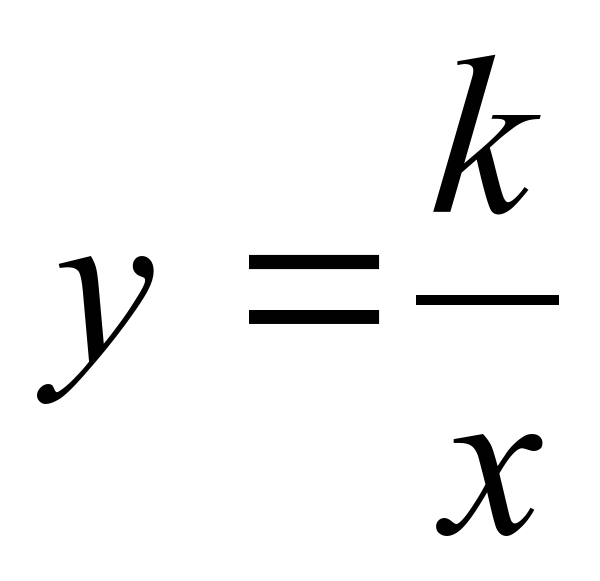 и рассмотреть свойства данной функции; развивать умение строить графики известных функций; формировать умение строить графики функций вида и рассмотреть свойства данной функции; развивать умение строить графики известных функций; формировать умение строить графики функций вида 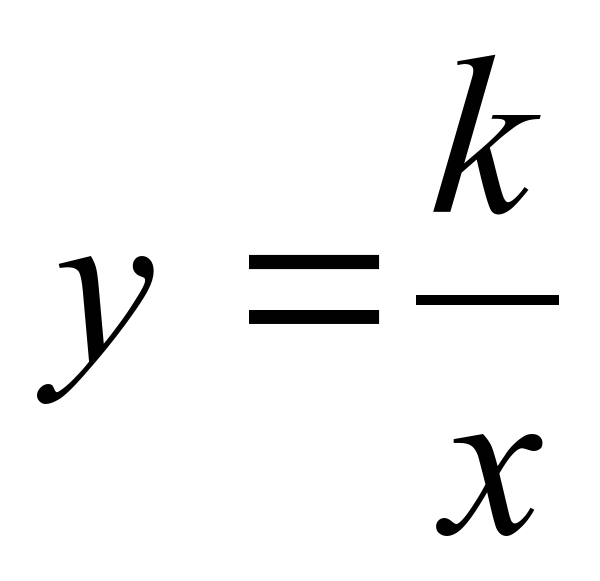 . . |
|
| 47 |
| Функция y= , её свойства и график , её свойства и график | Урок-практикум | Свойствах функции 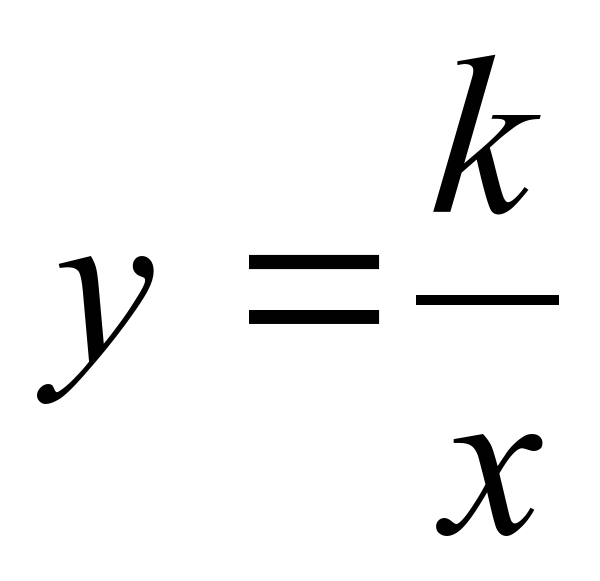 и умение строить график данной функции; ввести правила решения уравнений графическим способом; проверить умение строить графики функций, решать уравнения и системы уравнений. и умение строить график данной функции; ввести правила решения уравнений графическим способом; проверить умение строить графики функций, решать уравнения и системы уравнений. |
|
| 48 |
| Контрольная работа №4 | Урок проверки знаний |
|
|
| 49 |
| Как построить график функции у=f(x+t), если известен график функции у= f(x) | Урок изложения новой темы | Построения графика функции y=f(x+t), если известен график функции y=f(x); развивать умение строить графики различных функций. |
|
| 50 |
| Как построить график функции у=f(x+t), если известен график функции у= f(x) | Урок-практикум |
|
|
| 51 |
| Как построить график функции у=f(x)+m, если известен график функции у= f(x) | Урок изложения новой темы | Правило построения графика функции y=f(x)+m, если известен график функции y=f(x); формировать умение строить графики различных функций. |
|
| 52 |
| Как построить график функции у=f(x)+m, если известен график функции у= f(x) | Урок-практикум |
|
|
| 53 |
| Как построить график функции у=f(x+t)+m, если известен график функции у= f(x) | Урок изложения новой темы | Правило построения графика функции y=f(x+t)+m, если известен график функции y=f(x); формировать умение строить различных функций. |
|
| 54 |
| Как построить график функции у=f(x+t)+m, если известен график функции у= f(x) | Урок-практикум |
|
|
| 55 |
| Функция y=ax2+bx+c, её свойства и график | Урок изложения новой темы | Ввести алгоритм построения графика функции y = ax2+bx+c; рассмотреть свойства данной функции |
|
| 56 |
| Функция y=ax2+bx+c, её свойства и график | Урок-практикум |
|
|
| 57 |
| Функция y=ax2+bx+c, её свойства и график | Урок-практикум |
|
|
| 58 |
| Функция y=ax2+bx+c, её свойства и график | Урок актуализации знаний. |
|
|
| 59 |
| Графическое решение квадратных уравнений | Урок изложения новой темы | Квадратные уравнения графическим способом. |
|
| 60 |
| Контрольная работа №5 | Урок проверки знаний |
|
|
|
Учащиеся должны: |
| 1
| Знать: -графики функций у=kx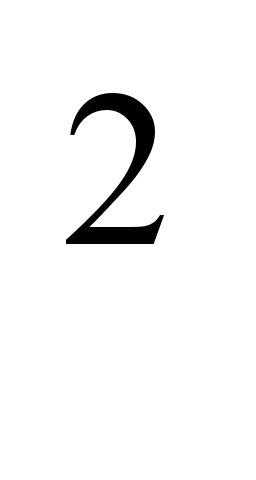 , у= , у=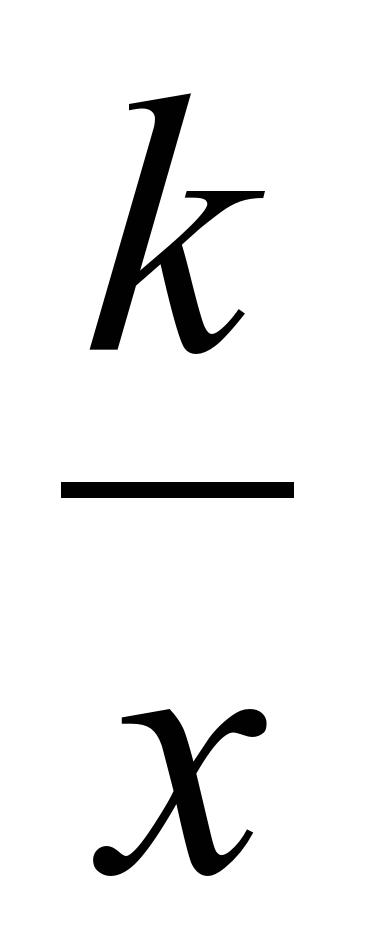 , описание с помощью графиков свойств этих функций; , описание с помощью графиков свойств этих функций; -алгоритм построения графиков функций у=f(x+t), у=f(x)+m, у=f(x+t)+m, у= -f(x), y=ax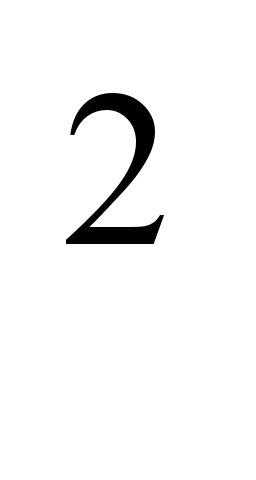 +bx+c; +bx+c; -уравнения оси симметрии параболы, служащей графиком квадратичной функции; -описывать словами процесс графического решения уравнения и процесс построения графика кусочной функции; -понимать смысл записи у= f(x). |
|
2 | Уметь: -вычислять конкретные значения функций у=kx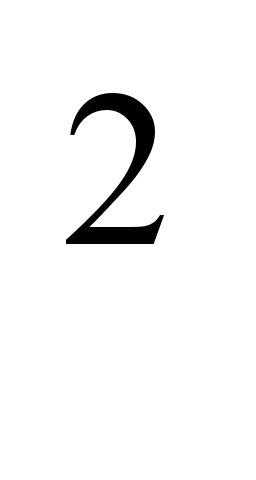 ,y= ,y= , y=ax2+bx+c и функций, заданных различными формулами на различных промежутках; , y=ax2+bx+c и функций, заданных различными формулами на различных промежутках; -строить графики функций с помощью параллельного переноса известных графиков; -составлять уравнение оси параболы, находить координаты вершины параболы, отвечать на вопрос о направлении ветвей параболы в зависимости от знака старшего коэффициента; -отвечать на вопрос о расположении гиперболы в зависимости от знака коэффициента k; -графически решать уравнения вида f(x)=g(x), где f(x) и g(x) – известные из курса функции; -находить наибольшее и наименьшее значение упомянутых выше функций на заданных промежутках; -читать графики; - решать задачи на функциональную символику. |
| Глава 4. Квадратные уравнения(20) |
| 61 |
| Основные понятия | Урок изложения новой темы | Ввести понятие квадратного уравнения, корня квадратного уравнения; показать решения квадратных уравнений; формировать умение решать квадратные уравнения. |
|
| 62 |
| Основные понятия | Урок-практикум |
|
|
| 63 |
| Формулы корней квадратных уравнений | Урок изложения новой темы | Показать способ решения полных квадратных уравнений с использованием формулы корней квадратного уравнения; формировать умение решать квадратные уравнения |
|
| 64 |
| Формулы корней квадратных уравнений | Урок-практикум | Алгоритм решения полных квадратных уравнений, понятие смысл дискриминанта; показать правила оформления решения задач с помощью квадратных уравнений; развивать умение решать квадратные уравнения. |
|
| 65 |
| Формулы корней квадратных уравнений | Урок-практикум |
|
|
| 66 |
| Рациональные уравнения | Урок изложения новой темы | Выработать алгоритм решения рациональных уравнений; формировать умение решать рациональные уравнения. |
|
| 67 |
| Рациональные уравнения | Урок-практикум |
|
|
| 68 |
| Рациональные уравнения | Урок-практикум |
|
|
| 69 |
| Контрольная работа №6 | Урок проверки знаний |
|
|
| 70 |
| Рациональные уравнения как математические модели реальных ситуаций | Урок изложения новой темы | Решать рациональные уравнения различной сложности; объяснить правила оформления решения задач, решающих с помощью рациональных уравнений; формировать умение решать и оформлять задачи. |
|
| 71 |
| Рациональные уравнения как математические модели реальных ситуаций | Урок-практикум |
|
|
| 72 |
| Рациональные уравнения как математические модели реальных ситуаций | Урок-практикум |
|
|
| 73 |
| Рациональные уравнения как математические модели реальных ситуаций | Урок актуализации знаний. |
|
|
| 74 |
| Частные случаи формулы корней квадратного уравнения | Урок изложения новой темы | Вывести формулы для решения квадратных уравнений с четным вторым коэффициентом; развивать умение решать квадратные уравнения, используя различные формулы. |
|
| 75 |
| Частные случаи формулы корней квадратного уравнения | Урок-практикум | Рассмотреть решение квадратных уравнений различного уровня сложности, с помощью разных формул; развивать умение решать квадратные уравнения и задачи с их применением. |
|
| 76 |
| Теорема Виете . Разложение квадратного трехчлена на линейные множители | Урок изложения новой темы | Доказать теорему Виета, показать ее применение; рассмотреть различные задания на применение теоремы Виета; сформировать умение использовать эту теорему. |
|
| 77 |
| Контрольная работа №7 | Урок проверки знаний |
|
|
| 78 |
| Иррациональные уравнения | Урок изложения новой темы | Ввести понятие иррациональных уравнений, равносильных уравнений; объяснить правило решения иррациональных уравнений и показать оформление решения; формировать умение решать иррациональные уравнения. |
|
| 79 |
| Иррациональные уравнения | Урок-практикум |
|
|
| 80 |
| Иррациональные уравнения | Урок актуализации знаний. |
|
|
|
Учащиеся должны: |
| 1
| Знать: -понятие квадратного уравнения и его видов (полное, неполное, приведенное, неприведенное); -дискриминант квадратного уравнения и его связь с числом действительных корней уравнения; -формулы корней квадратного уравнения; -теорему Виета; -разложение на множители квадратного трехчлена; -понятие о равносильности уравнений, о равносильных и неравносильных преобразованиях уравнений |
| 2 | Уметь: -применять различные формулы корней для решения квадратного уравнения; -решать рациональные ( в частности, биквадратные) уравнения, решать несложные иррациональные уравнения; -отсеивать посторонние корни; -четко выделять три этапа математического моделирования при решении текстовых задач. |
| Глава 5. Неравенства (15) |
| 81 |
| Свойства числовых неравенств | Урок изложения новой темы | Ввести свойства неравенства; формировать умение сравнивать числа и выражения, а так же умение пользоваться свойствами неравенств. |
|
| 82 |
| Свойства числовых неравенств | Урок-практикум |
|
|
| 83 |
| Свойства числовых неравенств |
|
|
|
| 84 |
| Исследование функций на монотонность | Урок изложения новой темы | Ввести понятие убывающей и возрастающей функций; формировать умение определять какой ( убывающей или возрастающей) является функция. |
|
| 85 |
| Исследование функций на монотонность | Урок-практикум |
|
|
| 86 |
| Исследование функций на монотонность | Урок актуализации знаний. |
|
|
| 87 |
| Решение линейных неравенств | Урок изложения новой темы | Правило решения и оформления линейных неравенств; формировать умение решать линейные неравенства. |
|
| 88 |
| Решение линейных неравенств | Урок-практикум |
|
|
| 89 |
| Решение квадратных неравенств | Урок изложения новой темы | Правила решение квадратных неравенств; формировать умение решать различные неравенства |
|
| 90 |
| Решение квадратных неравенств | Урок-практикум |
|
|
| 91 |
| Решение квадратных неравенств | Урок актуализации знаний. |
|
|
| 92 |
| Контрольная работа №8 | Урок проверки знаний |
|
|
| 93 |
| Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. | Урок изложения новой темы | Правила приближённого вычисления; формировать умение приближенно находить значения выражений. |
|
| 94 |
| Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. | Урок актуализации знаний. |
|
|
| 95 |
| Стандартный вид числа | Урок изложения новой темы | Ввести понятие и свойства степени с отрицательным целым показателем; формировать умение работать со степенями с целым показателем. |
|
| Учащиеся должны: |
| 1 | Знать: -свойства числовых неравенств; -первые представления о равносильности неравенств, о равносильных преобразованиях неравенств; -понятие возрастания и убывания функции, исследовать на монотонность функции y=kx + m,y=kx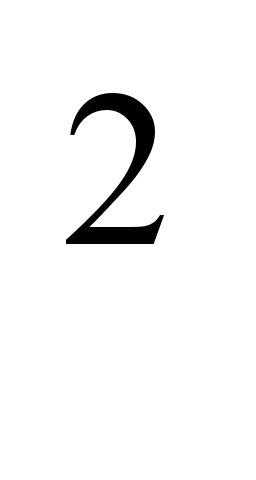 , y= , y= , y=ax2+bx+c, у=√х, у=|х|$ , y=ax2+bx+c, у=√х, у=|х|$ -понятие стандартного вида числа. |
| 2 | Уметь: -применять свойства числовых неравенств для доказательства неравенств, для решения линейных неравенств; -применять алгоритм решения квадратных неравенств; -находить приближенное значение действительного числа с заданной точностью. |
| Повторение (7)
|
| 96 |
| Алгебраические дроби | Урок-практикум |
|
|
| 97 |
| Степень | Урок-практикум |
|
|
| 98 |
| Квадратичная функция, квадратный корень | Урок-практикум |
|
|
| 99 |
| Итоговая контрольная работа | Урок проверки знаний |
|
|
| 100 |
| Повторение | Урок-практикум |
|
|
| 101 |
| Итоговый тест за курс 8 класса | Урок проверки знаний |
|
|
| 102 |
| Повторение | Урок-практикум |
|
|
















