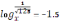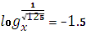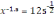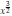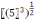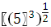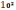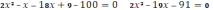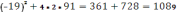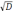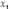I Саба?ты? та?ырыбы: ?арапайым логорифмдік те?деулер
II Саба?ты? ма?саты:
А. Білімділік: О?ушыларды? білімге деген к?з-?арасын ?алыптастыра отырып, математика?а деген ?ызы?ушылы?ын арттыру.
?. Дамытушылы?: О?ушыларды? математикалы? ой-?рісін дамыту.
Б. Т?рбиелік: О?ушыларды ал?ырлы??а, шапша?ды??а, ізденімпазды??а, тап?ырлы??а т?рбиелеу
III Саба?ты? барысы
1.?йымдастыру кезе?і
2. ?й тапсырмасын с?рау
А. Логарифмдік функцияны? ?асиеттері ж?не логарифмдік функцияны? графигі.
?.№60 (5,7) №64(2,3)
?ажайып ?штік
10
10
10
20
20
20
30
30
30
1. О? жа?та?ы 10 (x*y)
2. Ортада?ы 10 (x/y)
3. Сол жа?та?ы 10
4. О? жа?та?ы 20
Логарифмдік функция дегеніміз не?
5. Ортада?ы 20
а>0 бол?анда?ы логарифмдік функцияны? аны?талу облысы ж?не м?ндері жиыны
6. Сол жа?та?ы 20
0<а<1 бол?анда?ы логарифмдік функцияны? аны?талу облысы ж?не м?ндері жиыны
7. О? жа?та?ы 30 Y= функциясыны? графигін жаcа
8. Ортада?ы 30
Y= 4x функциясыны? графигін жаса
9. Сол жа?та?ы 30
Y=x т?зуіне ?атысты симметриялы?ын к?рсету
С?йкестік тесті
- =1
1.Х-ті тап
2.Х-ті тапlg(3x-5)=0
-
3?рнекті? м?нін тап
D(f) (-˜;-2.5[U]1~)
4.?рнекті? м?нін тап
+ log312
-
5.?рнекті? аны?талу айма?ын тап
-
6.?рнекті? аны?талу айма?ын тап
x=1/8
IV Жа?а та?ырып
?арапайым тригонометриялы? те?деулер
Айнымалысы логарифм та?басы астында болып келетін те?деулерді логарифмдік те?деулер деп атайды.
А) Б?л те?деулер логарифм аны?тамасын пайдаланып шешілетін ?арапайым те?деулер.
=b a>0 a≠1 x=
?) Потенциялдау ар?ылы шешілетін ?арапайым те?деулер
p>0
Саба?ты бекіту
№69
1 3
1-2х=3`
1-2х=3 =
-2х=3-1 =
-2х=2 x=5
Х=-1
№70
2. lg(X-9)+lg(2x-1)=2
lg(X-9)*(2x-1)=2
(X-9)(2x-1)=
D=
=+-33
=19-33/2*2=-14/4=-7/2
=19+33/2*2=52/4=13
Жауабы 13
V ?й ж?мысы №69 2,4,6 №70 1,3,5
?тілген та?ырып бойынша ?орытынды. ?арапайым логарифмдік те?деулерді шешуді? ?дістері.
Просмотр содержимого документа
«?арапайым логорифмдік те?деулер »
18.02.2015ж
I Сабақтың тақырыбы: Қарапайым логорифмдік теңдеулер
II Сабақтың мақсаты:
А. Білімділік: Оқушылардың білімге деген көз-қарасын қалыптастыра отырып, математикаға деген қызығушылығын арттыру.
Ә. Дамытушылық: Оқушылардың математикалық ой-өрісін дамыту.
Б. Тәрбиелік: Оқушыларды алғырлыққа, шапшаңдыққа, ізденімпаздыққа, тапқырлыққа тәрбиелеу
III Сабақтың барысы
1.Ұйымдастыру кезеңі
2. Үй тапсырмасын сұрау
А. Логарифмдік функцияның қасиеттері және логарифмдік функцияның графигі.
Ә.№60 (5,7) №64(2,3)
Ғажайып үштік
| 10 | 10 | 10 |
| 20 | 20 | 20 |
| 30 | 30 | 30 |
1. Оң жақтағы 10 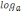
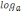 (x*y)
(x*y)
2. Ортадағы 10 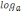
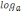 (x/y)
(x/y)
3. Сол жақтағы 10 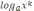
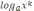
4. Оң жақтағы 20
Логарифмдік функция дегеніміз не?
5. Ортадағы 20
а0 болғандағы логарифмдік функцияның анықталу облысы және мәндері жиыны
6. Сол жақтағы 20
0
7. Оң жақтағы 30 Y=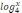
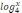 функциясының графигін жаcа
функциясының графигін жаcа
8. Ортадағы 30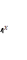
Y=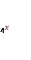 4x функциясының графигін жаса
4x функциясының графигін жаса
9. Сол жақтағы 30
Y=x түзуіне қатысты симметриялығын көрсету
Сәйкестік тесті
| 1.Х-ті тап 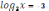 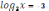 |
| 3Өрнектің мәнін тап 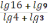 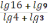
|
| 4.Өрнектің мәнін тап 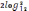 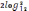 + log312 + log312
| x=2
|
| 5.Өрнектің анықталу аймағын тап 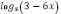
| 2 |
| 6.Өрнектің анықталу аймағын тап 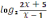 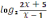
|
IV Жаңа тақырып
Қарапайым тригонометриялық теңдеулер
Айнымалысы логарифм таңбасы астында болып келетін теңдеулерді логарифмдік теңдеулер деп атайды.
А) Бұл теңдеулер логарифм анықтамасын пайдаланып шешілетін қарапайым теңдеулер.
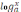
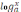 =b a0 a≠1 x=
=b a0 a≠1 x=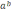
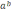
Ә) Потенциялдау арқылы шешілетін қарапайым теңдеулер
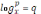
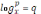 p0
p0 

Сабақты бекіту
№69
1 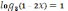
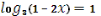 3
3 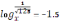
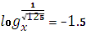
1-2х=3` 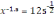
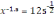
1-2х=3 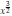
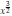 =
=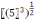
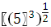
-2х=3-1 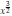
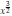 =
=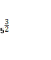
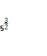
-2х=2 x=5
Х=-1
№70
2. lg(X-9)+lg(2x-1)=2
lg(X-9)*(2x-1)=2
(X-9)(2x-1)=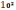
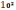
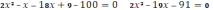
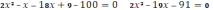
D=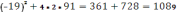
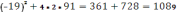
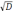
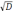 =+-33
=+-33
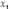
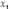 =19-33/2*2=-14/4=-7/2
=19-33/2*2=-14/4=-7/2

 =19+33/2*2=52/4=13
=19+33/2*2=52/4=13
Жауабы 13
V Үй жұмысы №69 2,4,6 №70 1,3,5
Өтілген тақырып бойынша қорытынды. Қарапайым логарифмдік теңдеулерді шешудің әдістері.

Жаңаөзен қаласы
№11 орта мектеп
Тақырыбы: Қарапайым логарифмдік теңдеулер.
Қалалық ашық сабақ
9 а-сыныбы.
Пән мұғалімі Карлова Зина
2014-2015 оқу жылы
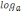
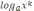
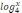
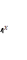
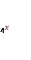 4x функциясының графигін жаса
4x функциясының графигін жаса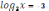
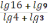
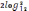
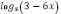
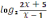
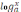
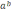
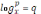

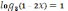
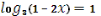 3
3